A2 Sonnenbrillen

Sonnenbrillen stellen für viele Menschen modische Accessoires dar. In erster Linie dienen sie allerdings dazu, die Augen der Trägerin oder des Trägers vor den Gefahren von Sonnenlicht zu schützen. Als Brillengläser dienen getönte Kunststoff- oder Glasscheiben, die mit filternden Schichten überzogen sind.

Die Sonne sendet weißes Licht aus. Beschreibe, was man in der Physik unter dem Begriff „weißes Licht“ versteht. Berechne die Wellenlänge des Lichts, dessen Photonen $Formula: 3,50\;\text{eV}$ $Formula: 3,50\;\text{eV}$ Energie haben, und begründe, dass diese Photonen für menschliche Augen gefährlicher sind als die des sichtbaren Lichts.

5 BE

Gib allgemein in Abhängigkeit von der Wellenlänge und der Ausbreitungsgeschwindigkeit die mathematische Beschreibung der zeitlichen und räumlichen Entwicklung einer ebenen harmonischen Welle an, die sich in Richtung der positiven Formula: x -Achse ausbreitet.

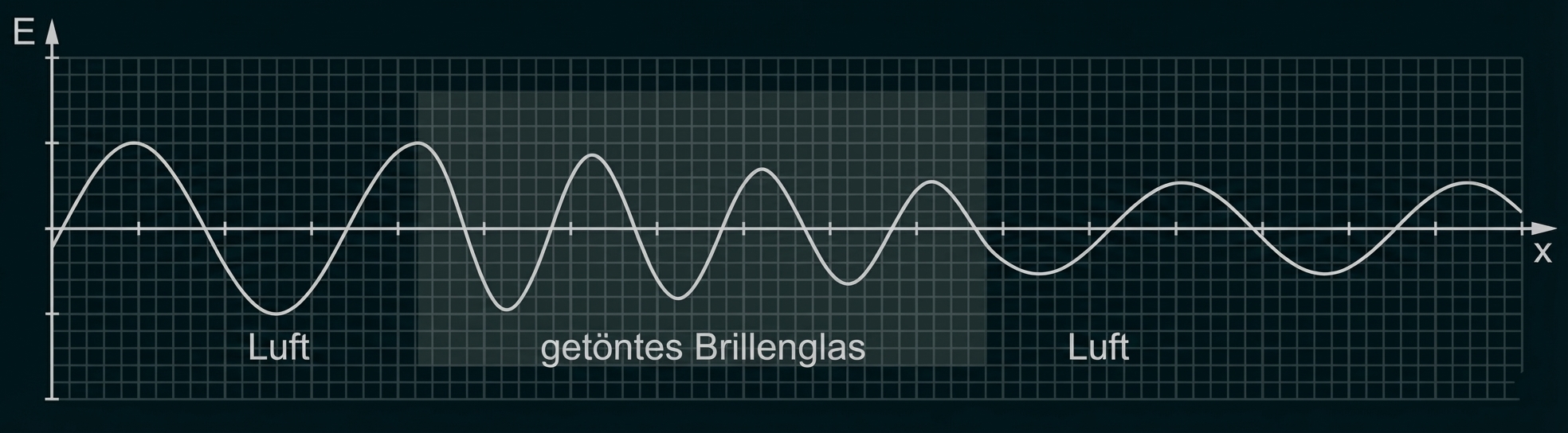
In Material 1 sind Veränderungen beschrieben, die sichtbares Licht beim Durchgang durch ein teilweise lichtdurchlässiges Material wie ein getöntes Brillenglas erfährt. Veranschauliche in Abb. 1b aus Material 1 die Veränderungen von Wellenlänge und Amplitude.

5 BE

Sonnenbrillengläser werden häufig mit dünnen, teilweise lichtdurchlässigen Schichten bedampft, um ihr Reflexions- und Transmissionsvermögen zu verändern (siehe Material 2).

Mache unter Einbeziehung von Material 1 plausibel, dass in die Formel zur Berechnung des Gangunterschieds $Formula: \Delta s$ $Formula: \Delta s$ der beiden Teilwellen aus Material 2 Abb. 2, die sich bei Formula: P überlagern, die Schichtdicke Formula: d, der Einfallswinkel $Formula: \alpha$ $Formula: \alpha$ und der Brechungsindex Formula: n der Beschichtung eingehen, ohne die quantitativen Beziehungen zu begründen.

4 BE

Der Brechungsindex des Beschichtungsmaterials soll Formula: n=1,22 betragen. Berechne für einen näherungsweise senkrechten Lichteinfall die kleinstmögliche Schichtdicke Formula: d, bei der Licht der Wellenlänge $Formula: 390\;\text{nm}$ $Formula: 390\;\text{nm}$ bei Formula: P ein Interferenzmaximum aufweist.

Berechne außerdem eine Wellenlänge von Licht, das bei dieser Schichtdicke bei Formula: P ein Interferenzminimum aufweist.

Ein Brillenglas wird mit einer Schicht dieser Schichtdicke Formula: d bedampft. Erläutere den Farbeindruck, den eine Person, die bei Sonnenlicht von vorne senkrecht auf die Oberfläche dieses Brillenglases blickt, von dem Brillenglas bekommt.

7 BE

In der Praxis besteht eine solche Beschichtung eines Brillenglases aus mehreren Lagen. Diese sind so gewählt, dass bei Formula: P Interferenzmaxima für möglichst viele Wellenlängen auftreten, insbesondere auch im sichtbaren Spektralbereich.

Beschreibe die Auswirkung einer solchen Beschichtung jeweils für den Brillenträger und für eine Person, die von vorne auf die Brille blickt.

Erläutere qualitativ, dass eine geeignete Beschichtung auf der dem Auge des Brillenträgers zugewandten Seite genutzt werden kann, damit der Brillenträger kein Spiegelbild des eigenen Auges im Brillenglas sieht.

4 BE

Bestimmte Brillengläser sind mit einer Schicht versehen, die das transmittierte Licht linear polarisiert (siehe Material 3).

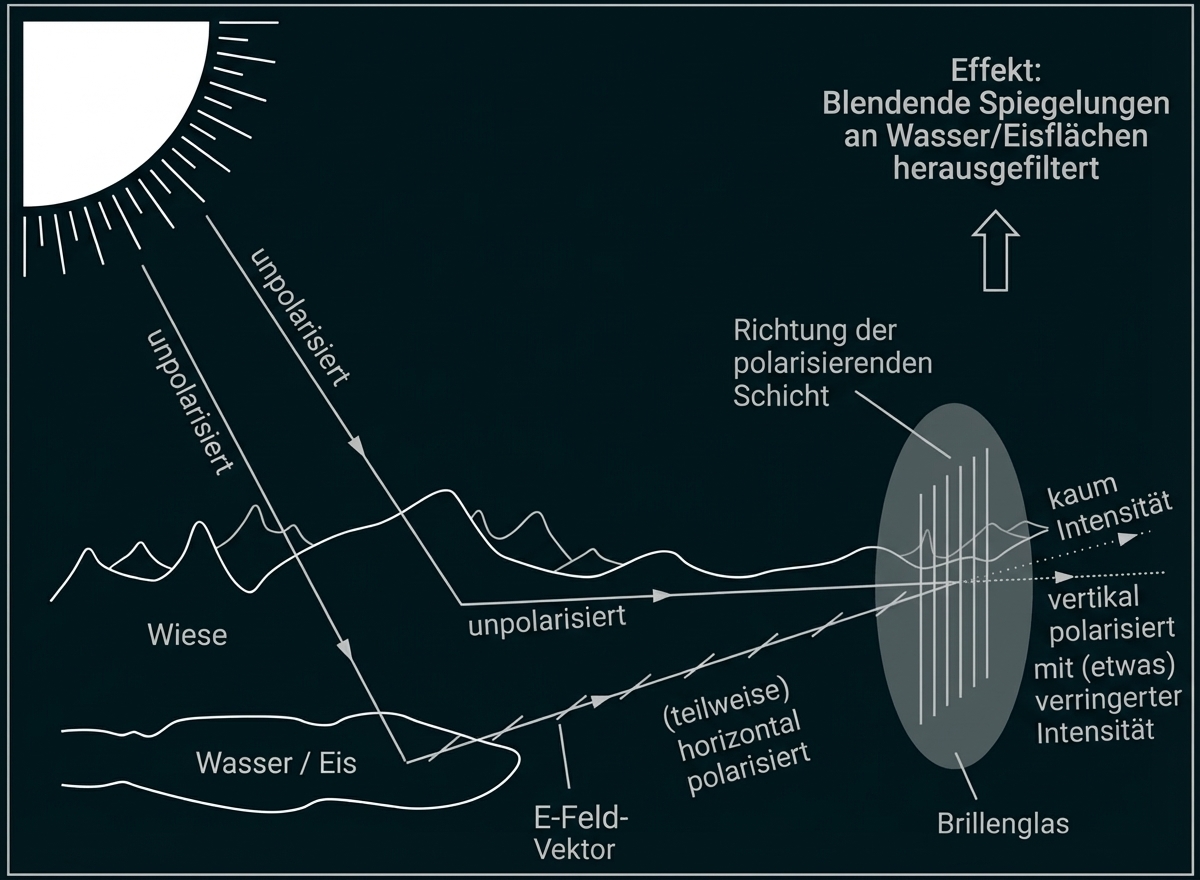
Stelle die Funktionsweise der polarisierenden Schicht in einem beschrifteten Bild anschaulich dar. Gestalte deine Darstellung so, dass du diese für eine Präsentation in deinem Physikkurs verwenden könntest. Gib auch die Polarisationsrichtung an, die die polarisierende Schicht erzeugen muss.

8 BE

Sebastian möchte eine Sonnenbrille kaufen, die er für seine ausgedehnten Mountainbike-Touren im Sommer ebenso nutzen kann wie für Skitouren im Winter. Zwei Sonnenbrillen sind für ihn in der engeren Auswahl: Eine Sonnenbrille mit polarisierenden Gläsern und leichter Tönung sowie CE-Siegel oder eine Sonnenbrille mit sehr starker Tönung und UV-400-Kennzeichnung, aber ohne polarisierende Schicht.

Entscheide unter Verwendung der Materialien 3 und 4 mithilfe einer Nutzwertanalyse anhand von drei Kriterien, für welche Sonnenbrille er sich entscheiden sollte.

Erläutere eine weitere Eigenschaft einer Sonnenbrille, auf die Sebastian mit Blick auf seine gewünschten Anwendungsbereiche unbedingt Wert legen sollte.

7 BE

40 BE

Material 1: Ausbreitung von Licht

Beim Übergang von sichtbarem Licht aus Luft in teilweise lichtdurchlässige Materialien bleibt seine Frequenz gleich, während die Ausbreitungsgeschwindigkeit beim Eintritt in das Material kleiner wird und sich die Amplitude der Wellenfunktion beim Durchlaufen des Materials verringert. In den Abbildungen 1a und 1b ist eine Komponente Formula: E der elektrischen Feldstärke in Abhängigkeit vom Ort Formula: x für eine Lichtwelle im sichtbaren Bereich dargestellt.

Abb. 1a: Ausbreitung in Luft

Wellenfunktion von Licht mit Eintritt in Materie

Abb. 1b: Ausbreitung durch ein getöntes Brillenglas

Material 2: Reflektierende Beschichtung eines Brillenglases

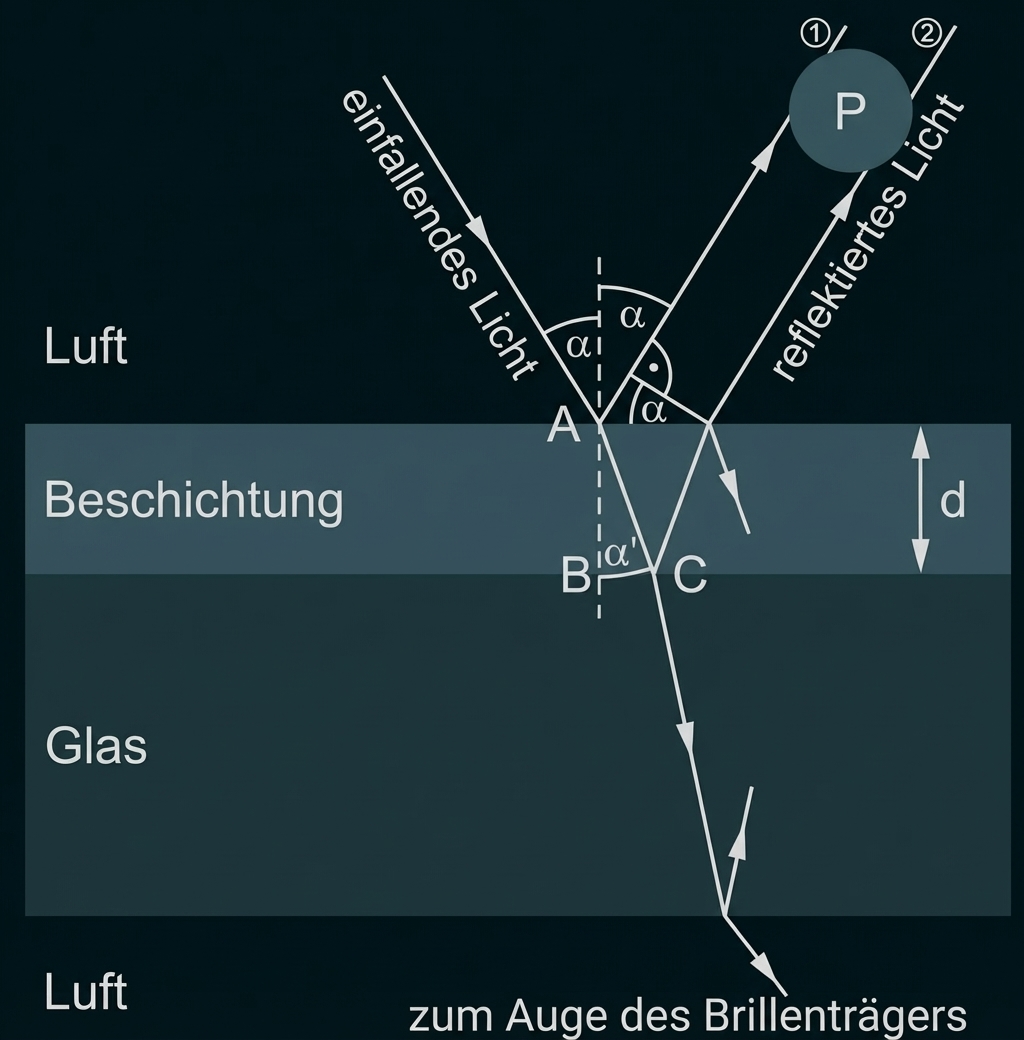
Beim Durchgang von Licht durch teilweise lichtdurchlässige Schichten treten an Grenzflächen Reflexion und Brechung auf. Abb. 2 zeigt den Lichtweg durch eine solche Schicht. Die im Bild mit Formula: (1) und Formula: (2) gekennzeichneten reflektierten Lichtstrahlen liegen in der Realität an der mit Formula: P markierten Stelle nahezu aufeinander.

Sichtbares Licht hat in teilweise lichtdurchlässiger Materie eine kleinere Ausbreitungsgeschwindigkeit als im Vakuum. Der Brechungsindex Formula: n gibt das Verhältnis dieser Geschwindigkeiten an. In Luft gilt $Formula: n_{\text {Luft }} \approx 1,$ $Formula: n_{\text {Luft }} \approx 1,$ in Beschichtungen von Brillengläsern gilt $Formula: n\gt1.$ $Formula: n\gt1.$

Der Gangunterschied $Formula: \Delta s$ $Formula: \Delta s$ der Teilwellen Formula: (1) und Formula: (2) an der Stelle Formula: P kann berechnet werden durch $Formula: \Delta s=2 d \cdot \sqrt{n^2-(\sin \alpha)^2}.$ $Formula: \Delta s=2 d \cdot \sqrt{n^2-(\sin \alpha)^2}.$

Abb. 2: Lichtweg durch eine teilweise lichtdurchlässige Schicht

Material 3: Polarisation bei Transmission und Reflexion

Sonnenbrillen mit polarisierenden Brillengläsern laden viele Menschen zum "Spielen" ein, weil sich Helligkeiten und Kontraste verändern, wenn man durch das Brillenglas sieht und die Brille um die Sichtachse dreht. Diese Brillengläser sind mit einer Schicht versehen, die aus dem unpolarisierten Sonnenlicht linear polarisiertes Licht macht. Die Schicht ist nur für die Komponenten der einfallenden elektromagnetischen Wellen durchlässig, deren elektrisches Feld parallel zur von der Schicht vorgegebenen Polarisationsrichtung ist. Die polarisierende Schicht reduziert dadurch die Intensität des Lichts, das das Brillenglas durchdringt.

Für den Sehkomfort ist folgender Effekt besonders von Bedeutung: Die Grundlage ist ein zusätzlicher Polarisationsvorgang, der auftritt, wenn Sonnenlicht von Gegenständen reflektiert wird. Wenn unpolarisiertes Licht an einer ebenen Grenzfläche zwischen zwei Materialien reflektiert wird, ist das reflektierte Licht teilweise polarisiert (siehe Abb. 3). Der Grad der Polarisation hängt vom Einfallswinkel $Formula: \theta$ $Formula: \theta$ und den Brechungsindizes der beiden Materialien ab. Für einen bestimmten Einfallswinkel $Formula: \theta_P$ $Formula: \theta_P$ bilden die Richtungen des reflektierten und des gebrochenen Lichts einen rechten Winkel. Für $Formula: \theta \geq \theta_P$ $Formula: \theta \geq \theta_P$ ist das reflektierte Licht fast vollständig polarisiert, und zwar mit einer Polarisationsrichtung des elektrischen Feldes parallel zur Grenzfläche.

Im Alltag tritt diese Polarisation des reflektierten Lichts häufig an der Grenzfläche zwischen Luft und Wasser bzw. Eis auf. Da polarisierende Brillengläser dieses reflektierte Licht ganz oder teilweise herausfiltern, ermöglichen sie ein blendarmes, kontrastreiches Sehen mit einer verbesserten Farbwahrnehmung, was der Brillenträger als erhöhten Sehkomfort wahrnimmt.

Polarisation von Lichtstrahlen bei Reflexion

Abb. 3: Polarisation bei Reflexion

Material 4: Tönung von Brillengläsern

Die sogenannte Tönung von Brillengläsern beschreibt deren Absorptionseigenschaften im sichtbaren Spektralbereich. Sonnenbrillengläser werden in fünf Kategorien (siehe Tabelle) eingeteilt. Der Absorptionsgrad gibt dabei den Anteil der einfallenden Lichtenergie an, der vom Brillenglas absorbiert wird.

Kategorie	Absorptionsgrad im sichtbaren Spektralbereich	Eignung
	$Formula: \lt20\,\%$ $Formula: \lt20\,\%$	an bewölkten Tagen und an Abenden
	$Formula: 20-57\,\%$ $Formula: 20-57\,\%$	an Frühlingstagen, bei wechselndem Wetter
	$Formula: 57-82\,\%$ $Formula: 57-82\,\%$	normaler Blendschutz für den Sommer in Mitteleuropa
	$Formula: 82-92\,\%$ $Formula: 82-92\,\%$	Südeuropa, Strand, Berge, Lesen in der Sonne
	$Formula: \gt92\,\%$ $Formula: \gt92\,\%$	Hochgebirge, Gletscher

Da für die Brillenträgerin bzw. den Brillenträger die Umgebung abgedunkelt erscheint, weiten sich die Pupillen und die Augen werden nicht mehr zugekniffen. Das Sehen wird insgesamt als weniger anstrengend wahrgenommen und damit verbundene Probleme wie Kopfschmerzen sind weniger häufig bzw. intensiv.

Über die Absorption im UV-Bereich gibt das CE-Siegel auf der Sonnenbrille Auskunft: Es wird nur vergeben, wenn die Brille einen 100-prozentigen UV-Filter für Licht mit Wellenlängen kleiner als $Formula: 380\;\text{nm}$ $Formula: 380\;\text{nm}$ hat.

Die zusätzliche Kennzeichnung „UV 400“ erhält die Brille dann, wenn alle Wellenlängen unterhalb von $Formula: 400\;\text{nm}$ $Formula: 400\;\text{nm}$ herausgefiltert werden.

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?

„Weiß“ ist eine physiologische Farbempfindung, mit der der Mensch eine Mischung der physikalisch vorhandenen Spektralfarben („Regenbogenfarben“) wahrnimmt. Dieses spektrale Licht ist elektromagnetische Strahlung, die von Atomen und Molekülen z. B. der Sonne emittiert wird. Der sichtbare Bereichs des Spektrums umfasst dabei Wellenlängen zwischen $Formula: 380\;\text{nm}$ $Formula: 380\;\text{nm}$ und $Formula: 780\;\text{nm},$ $Formula: 780\;\text{nm},$ entsprechend einer Photonenenergie von rund $Formula: 1,6\;\mathrm{eV}$ $Formula: 1,6\;\mathrm{eV}$ bis $Formula: 3,2\;\mathrm{eV}.$ $Formula: 3,2\;\mathrm{eV}.$

Für die Photonenenergie gilt die Beziehung $Formula: E_{\text {Photon}}=\tfrac{h\cdot c}{\lambda}.$ $Formula: E_{\text {Photon}}=\tfrac{h\cdot c}{\lambda}.$ Damit wird für die Energie $Formula: 3,50\;\mathrm{eV}$ $Formula: 3,50\;\mathrm{eV}$ die Wellenlänge

$Formula: \lambda=\dfrac{h \cdot c}{E_{\text {Photon}}}$ $Formula: \lambda=\dfrac{h \cdot c}{E_{\text {Photon}}}$ $Formula: =\frac{6,63 \cdot 10^{-34}\;\mathrm{Js} \cdot 3,00 \cdot 10^8\;\tfrac{\mathrm{m}}{\mathrm{s}}}{3,50 \cdot 1,60 \cdot 10^{-19}\;\mathrm{J}}=355\;\mathrm{nm}$ $Formula: =\frac{6,63 \cdot 10^{-34}\;\mathrm{Js} \cdot 3,00 \cdot 10^8\;\tfrac{\mathrm{m}}{\mathrm{s}}}{3,50 \cdot 1,60 \cdot 10^{-19}\;\mathrm{J}}=355\;\mathrm{nm}$

erhalten. Licht dieser Wellenlänge liegt im UV-Bereich und besitzt eine größere Energie als sichtbares Licht. Daher kann speziell die Netzhaut des menschlichen Auges, die auf die Verarbeitung sichtbaren Lichts ausgelegt ist, durch eintreffendes energiereiches UV-Licht geschädigt werden.

Wellengleichung

Für die beschriebene räumliche und zeitliche Welle gilt die Gleichung:

$Formula: y(x ; t)=y_{\max } \cdot \sin \left[2 \pi \cdot\left(\frac{c}{\lambda} \cdot t-\frac{x}{\lambda}\right)\right]$ $Formula: y(x ; t)=y_{\max } \cdot \sin \left[2 \pi \cdot\left(\frac{c}{\lambda} \cdot t-\frac{x}{\lambda}\right)\right]$

Veränderungen von Wellenlänge und Amplitude

Wellenänderung von Licht bei Eintritt in ein Medium

Der Gangunterschied $Formula: \Delta s$ $Formula: \Delta s$ ist durch die Summe der Kantenlängen in dem in der Abbildung rechts hervorgehobenen Dreieck gegeben.

Einfallswinkel $Formula: \alpha:$ $Formula: \alpha:$

Ändert sich $Formula: \alpha,$ $Formula: \alpha,$ dann ändert sich auch der (wegen der höheren optischen Dichte kleinere) Brechungswinkel $Formula: \alpha'.$ $Formula: \alpha'.$ Damit ändert sich im Dreieck Formula: ABC auch die Hypotenusenlänge $Formula: \tfrac{\Delta s}{2}$ $Formula: \tfrac{\Delta s}{2}$ und folglich der Gangunterschied $Formula: \Delta s.$ $Formula: \Delta s.$

Schichtdicke Formula: d:

Da Formula: d eine Kathete im Dreieck Formula: ABC bildet, bewirkt eine Änderung von auch eine Änderung der Hypotenuse und damit von $Formula: \Delta s.$ $Formula: \Delta s.$

Brechungsindex Formula: n:

Wird ein Beschichtungsmaterial mit verändertem Brechungsindex verwendet, ändert sich der Brechungswinkel $Formula: \alpha'$ $Formula: \alpha'$ und damit, wie oben ausgeführt, auch $Formula: \Delta s.$ $Formula: \Delta s.$

Fazit: Der Gangunterschied $Formula: \Delta s$ $Formula: \Delta s$ hängt von den drei Größen $Formula: \alpha, d$ $Formula: \alpha, d$ und Formula: n ab.

Gangunterschied bei einfallendem Licht auf ein beschichtetes Glas

Näherungsweise senkrecht bedeutet $Formula: \alpha \approx 0,$ $Formula: \alpha \approx 0,$ für die Schichtdicke gilt wegen Formula: n=1,22 also:

$Formula: \Delta s=2 d \cdot \sqrt{n^2}=2 d \cdot n$ $Formula: \Delta s=2 d \cdot \sqrt{n^2}=2 d \cdot n$ $Formula: =2 d \cdot 1,22$ $Formula: =2 d \cdot 1,22$

Zudem ist für das erste Interferenzmaximum der Gangunterschied gerade eine ganze Wellenlänge: $Formula: \Delta s=\lambda_{\max }.$ $Formula: \Delta s=\lambda_{\max }.$

Mit $Formula: \lambda_{\max }=390\;\mathrm{nm}$ $Formula: \lambda_{\max }=390\;\mathrm{nm}$ folgt für die minimale Schichtdicke durch Einsetzen in die obige Gleichung:

$Formula: 390\;\mathrm{nm}=2 d_{\min} \cdot 1,22$ $Formula: 390\;\mathrm{nm}=2 d_{\min} \cdot 1,22$ $Formula: \Rightarrow d_{\min }=\dfrac{390\;\mathrm{nm}}{2 \cdot 1,22}=160\;\mathrm{nm}$ $Formula: \Rightarrow d_{\min }=\dfrac{390\;\mathrm{nm}}{2 \cdot 1,22}=160\;\mathrm{nm}$

Ein Interferenzminimum ergibt sich, wenn der Gangunterschied ein ungeradzahliges Vielfache der halben Wellenlänge ist, also z. B. für

$Formula: \Delta s=\dfrac{\lambda_{\min }}{2} \Rightarrow \lambda_{\min } =2 \cdot \Delta s$ $Formula: \Delta s=\dfrac{\lambda_{\min }}{2} \Rightarrow \lambda_{\min } =2 \cdot \Delta s$ $Formula: =2 \cdot 390\;\mathrm{nm}=780\;\mathrm{nm}.$ $Formula: =2 \cdot 390\;\mathrm{nm}=780\;\mathrm{nm}.$

Licht der Wellenlänge $Formula: \lambda_{\max }=390\;\mathrm{nm}$ $Formula: \lambda_{\max }=390\;\mathrm{nm}$ erscheint blau, Licht der Wellenlänge $Formula: \lambda_{\text {min}}=780\;\mathrm{nm}$ $Formula: \lambda_{\text {min}}=780\;\mathrm{nm}$ erscheint rot. Insgesamt werden im reflektierten Licht am Punkt Formula: P die roten Anteile des ursprünglichen weißen Lichts („weiß Formula: = rot + grün + blau") geschwächt werden und blaue verstärkt. Das Brillenglas erscheint daher für den am Punkt befindlichen Beobachter blau-grün getönt.

Brillenträger:

Die an den Schichten reflektierten Strahlen gelangen nicht ins Auge. Daher wird durch die Reflexion die Intensität und damit die Helligkeit des transmittierten Lichts verringert; der Brillenträger sieht alles dunkler.

Betrachter vor der Brille:

Wegen der hohen Reflexionsrate mit möglichst vielen Wellenlängen (hohe Farbmischung → weißes Licht) erscheinen dem Betrachter die Brillengläser wie ein Spiegel.

Vermeidung der Spieglung des Auges:

Das gelingt dann, wenn der in Teilaufgabe b beschriebene Effekt der konstruktiven Verstärkung gerade nicht ermöglicht wird. Die Schichtdicken müssen also so gewählt sein, dass stattdessen destruktive Interferenz stattfindet, sodass die nach innen reflektierten Strahlen sich möglichst gegenseitig auslöschen.

Schaubild der Funktionsweise einer polarisierenden Schicht

Zunächst werden anhand der Aufgaben- und Materialtexte drei Kriterien definiert, nach denen die Eignung der Sonnenbrille geprüft werden soll. Hier bieten sich an:

a) guter UV-Schutz

b) Sehkomfort

c) Vermeidung von Blendung

Die zugehörigen Brilleneigenschaften zur Erfüllung dieser Kriterien sind:

a) CE-Siegel / UV-400-Kennzeichnung

b) Stärke der Tönung

c) polarisierende Gläser

Die Einsatzgebiete und -zeiten, in denen Sebastian die Brille benötigt, sind:

Sommer: Mountainbike-Touren
Winter: Skitouren

Zur Auswahl stehen zwei Brillen mit folgenden Eigenschaften:

polarisierende Gläser, leichte Tönung, CE-Siegel
keine polarisierende Gläser, sehr starke Tönung, UV-400-Kennzeichnung

Es wird deutlich, dass keine der beiden Brillen alle Kriterien in gleichem Maß erfüllt. Daher muss Sebastian eine Gewichtung der Kriterien vornehmen, also anhand des Einsatzzweckes festlegen, welche der Kriterien ihm am wichtigsten bzw. weniger wichtig erscheinen. Beispielsweise kann er folgendermaßen argumentieren:

Die UV-Einstrahlung ist im Sommer in den Bergen, vor allem aber im Winter auf schneereichen Skipisten (Reflexion!) in den oberen Gebirgsregionen sehr groß. Daher ist ein optimaler UV-Schutz der Augen am wichtigsten.
Ebenso ist auf den sonnenreichen und reflektierenden Pisten mit Blick auf die Konzentrationsfähigkeit bei der aktiven Sportausübung das möglichst entspannte Sehen wichtig. Das erfordert eine starke Tönung der Gläser.
Die Reduzierung von Blendeffekten ist zwar grundsätzlich wünschenswert, diese treten aber beim Mountainbiken und beim Skifahren (anders als etwa beim Wassersport) nicht gravierend in Erscheinung.

Die ersten beiden Argumente sprechen eindeutig für Brille 2. Das dritte Argument wertet die an sich wünschenswerte Polarisation der Gläser bei Brille 1 als vergleichsweise weniger bedeutsam ein.

Fazit: Sebastian sollte sich für Brille 2 entscheiden.

Weitere mögliche Kriterien, welche die Kaufentscheidung beeinflussen:

Gläsergröße (um ein möglichst großes Gesichtsfeld zu gewährleisten)
Preis
Gewicht/Tragekomfort/Passform
Robustheit (Beanspruchung durch Sportarten)

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?