A4 Kernphysik Medizin

Das Iridium-Isotop $Formula: ^{192}\text{Ir}$ $Formula: ^{192}\text{Ir}$ ist ein $Formula: \beta^-$ $Formula: \beta^-$ -Strahler mit einer Halbwertszeit von Formula: 73,8 Tagen. Die Atommasse von $Formula: ^{192}\text{Ir}$ $Formula: ^{192}\text{Ir}$ beträgt $Formula: 191,962602\;\text{u}.$ $Formula: 191,962602\;\text{u}.$

Stelle die Zerfallsgleichung für $Formula: ^{192}\text{Ir}$ $Formula: ^{192}\text{Ir}$ auf und berechne die bei dieser Reaktion freiwerdende Energie.

[zur Kontrolle: $Formula: Q = 1,46\;\text{MeV}$ $Formula: Q = 1,46\;\text{MeV}$ ]

4 BE

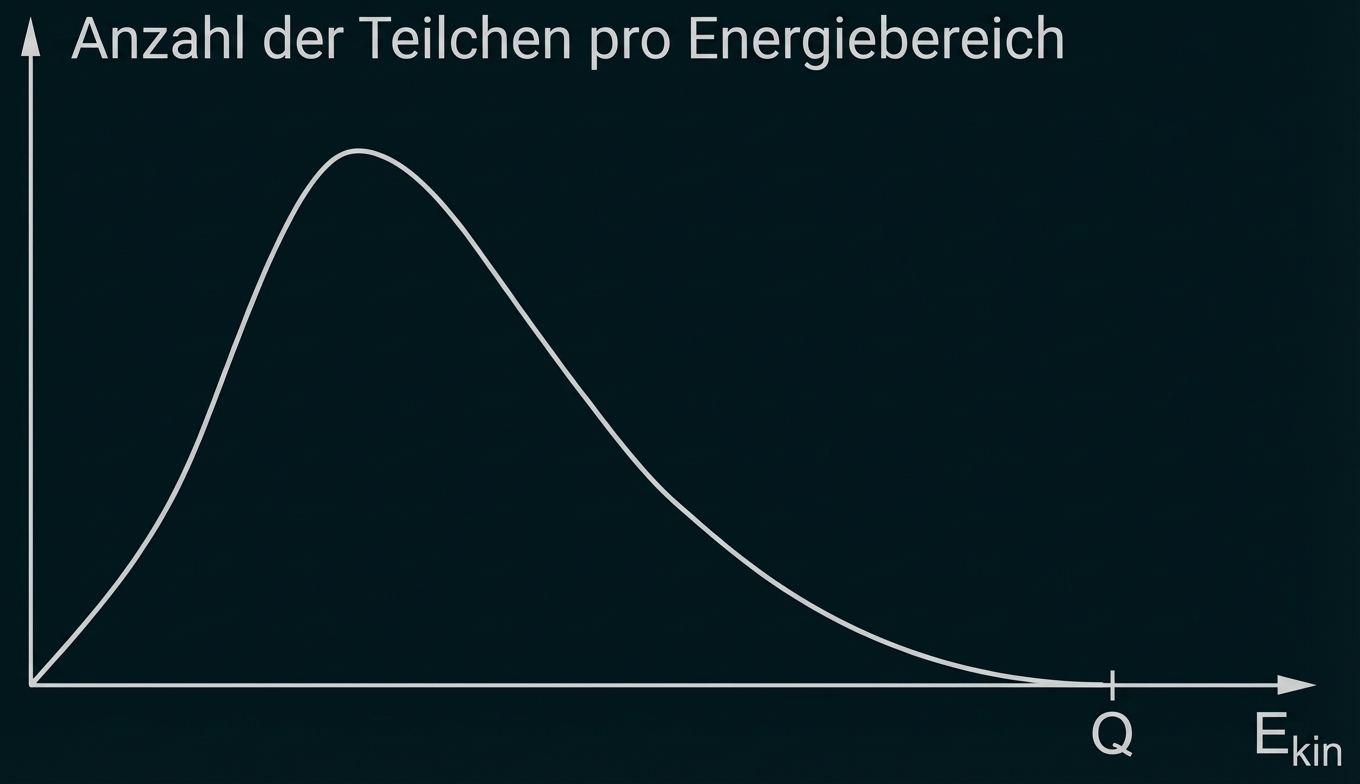
Skizziere die Verteilung der kinetischen Energie der $Formula: \beta^-$ $Formula: \beta^-$ -Teilchen bei diesem Zerfall in einem Diagramm und ergänze den Formula: Q -Wert an passender Stelle. Begründe die Wahl der Stelle für den -Wert.

5 BE

Der Tochterkern von $Formula: ^{192}\text{Ir}$ $Formula: ^{192}\text{Ir}$ sendet sofort nach seiner Entstehung $Formula: \gamma$ $Formula: \gamma$ -Quanten aus, deren Absorption durch Materie mithilfe der Versuchsanordnung aus Material 1 Abb. 1 genauer untersucht wird.

Begründe, dass der Abstand Formula: s zwischen Präparat und Zählrohr während der Messung nicht verändert werden darf, und ermittle aus Material 1 Abb. 2 die Halbwertsdicke $Formula: D_\tfrac{1}{2}$ $Formula: D_\tfrac{1}{2}$ von Blei für die im Experiment verwendete $Formula: \gamma$ $Formula: \gamma$ -Strahlung.

4 BE

Zeige mithilfe von Material 1, dass für den Zusammenhang zwischen Schwächungskoeffizient $Formula: \mu$ $Formula: \mu$ und Halbwertsdicke $Formula: D_\tfrac{1}{2}$ $Formula: D_\tfrac{1}{2}$ gilt:

$Formula: D_\tfrac{1}{2}=\dfrac{\ln 2}{\mu}$ $Formula: D_\tfrac{1}{2}=\dfrac{\ln 2}{\mu}$

4 BE

Ermittle mithilfe von Material 2 Abb. 3 den Wert des Schwächungskoeffizienten $Formula: \mu$ $Formula: \mu$ mit Angabe der Messunsicherheiten. Bestimme damit unter Berücksichtigung der Fortpflanzung der Messunsicherheiten das Intervall, in dem die Halbwertsdicke liegt, und vergleiche die Ergebnisse mit deinem Ergebnis aus Teilaufgabe c.

9 BE

Gib einen Grund dafür an, dass die Absorptionskurve in Material 3 Abb. 4 auch zur Beschreibung der Absorption im menschlichen Körper verwendet werden kann. Begründe mithilfe von Material 3, dass es sinnvoll ist, in Schutzkleidung, die vor $Formula: \gamma$ $Formula: \gamma$ -Strahlung schützen soll, Blei einzuarbeiten.

3 BE

Ein Tumor soll in der Brachytherapie mit $Formula: ^{192}\text{Ir}$ $Formula: ^{192}\text{Ir}$ behandelt werden (siehe Material 4). Der Tumor soll als kugelförmig mit Radius $Formula: 3,0\;\text{cm}$ $Formula: 3,0\;\text{cm}$ und Masse $Formula: 120\;\text{g}$ $Formula: 120\;\text{g}$ angenommen werden. Die Aktivität des Strahlers wurde exakt 48 Stunden vor dem Zeitpunkt der Behandlung zuletzt bestimmt. Man erhielt als Wert $Formula: A_0 = 220\;\text{GBq}.$ $Formula: A_0 = 220\;\text{GBq}.$ Zu diesem Zeitpunkt wäre für die Therapie des Tumors eine Bestrahlungszeit von 720 Sekunden nötig gewesen, um die von der Ärztin bzw. vom Arzt festgelegte Energiedosis aufzunehmen.

Bestimme die Aktivität zum Zeitpunkt der Bestrahlung und die angepasste Bestrahlungszeit. Gehe vereinfachend davon aus, dass sich die Aktivität während der Behandlung nicht verändert.

5 BE

Schätze mithilfe von Material 3 die vom Tumor aufgenommene Äquivalentdosis durch $Formula: \gamma$ $Formula: \gamma$ -Strahlung ab. Gib die dabei getroffenen Annahmen an.

4 BE

40 BE

Material 1: Absorption von $Formula: \color{#287882}{\boldsymbol{\gamma}}$ $Formula: \color{#287882}{\boldsymbol{\gamma}}$ -Strahlung durch Materie

Mit der vom Tochterkern des $Formula: ^{192}\text{Ir}$ $Formula: ^{192}\text{Ir}$ emittierten $Formula: \gamma$ $Formula: \gamma$ -Strahlung werden Absorptionsmessungen an Bleiplatten verschiedener Dicke durchgeführt (vgl. Abb. 1). Dazu wird die Anzahl Formula: N der vom Zählrohr in einem festgelegten Zeitintervall registrierten $Formula: \gamma$ $Formula: \gamma$ -Quanten in Abhängigkeit von der Dicke Formula: d der Bleiplatten (Absorberdicke) bestimmt. Die Absorptionsfähigkeit eines Materials für radioaktive Strahlung wird durch die sogenannte Halbwertsdicke $Formula: D_\tfrac{1}{2}$ $Formula: D_\tfrac{1}{2}$ charakterisiert. Darunter versteht man die Dicke des Materials, bei der die Hälfte der Strahlung absorbiert wurde.

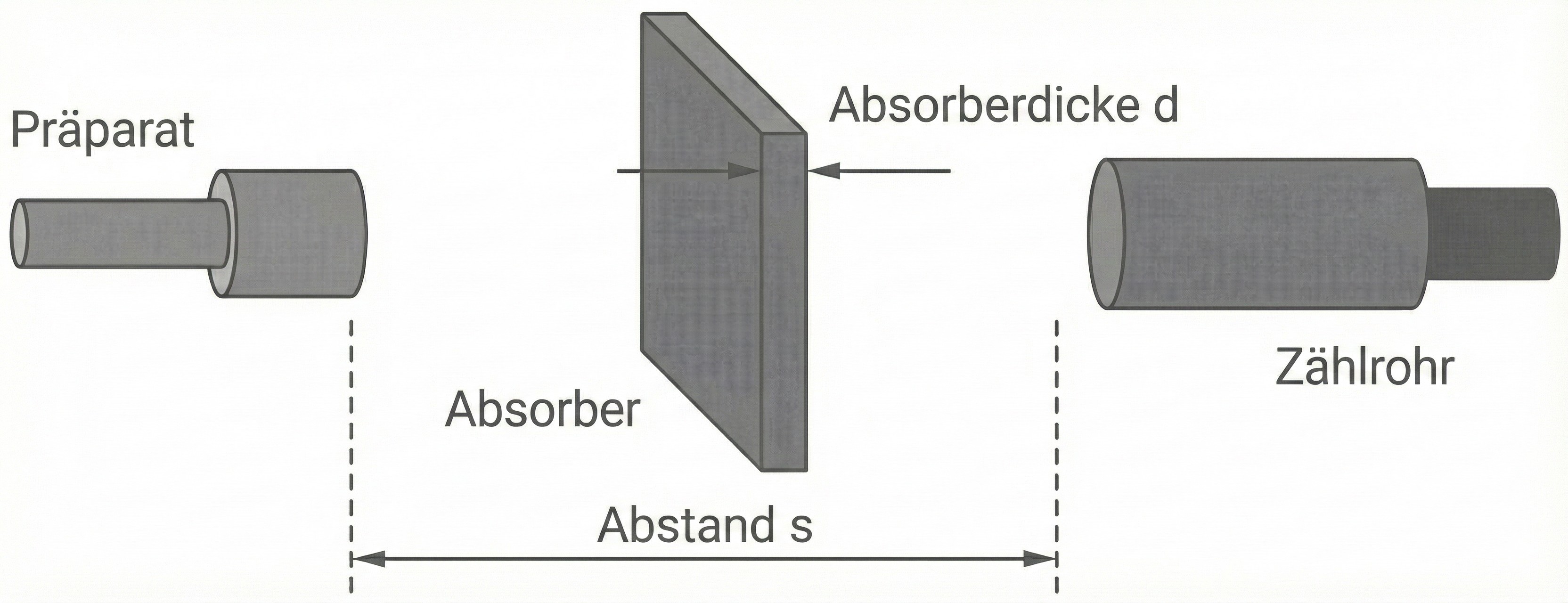
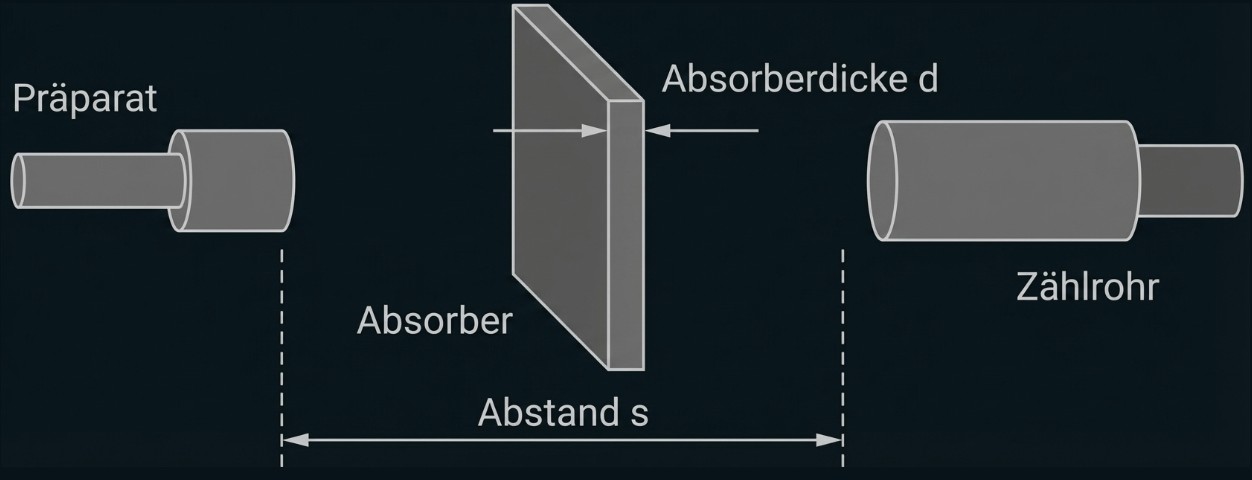
Schematische Darstellung: Präparat links, Absorber (Dicke d) in der Mitte, Zählrohr rechts, Abstand s.

Abb. 1

Für Blei sind die um die Nullrate bereinigten Messwerte mit ihren jeweiligen Messunsicherheiten in Abb. 2 dargestellt.

Abb. 2: Absorptionskurve für Blei

Der Zusammenhang zwischen der Anzahl Formula: N der registrierten $Formula: \gamma$ $Formula: \gamma$ -Quanten und der Absorberdicke Formula: d kann durch $Formula: N(d)=N_0 \cdot \mathrm e^{-\mu \cdot d}$ $Formula: N(d)=N_0 \cdot \mathrm e^{-\mu \cdot d}$ beschrieben werden. Dabei ist Formula: N_0 die Anzahl der registrierten $Formula: \gamma$ $Formula: \gamma$ -Quanten im Abstand Formula: s ohne Absorber und $Formula: \mu$ $Formula: \mu$ der sogenannte Schwächungskoeffizient.

Material 2: Schwächungskoeffizient von Blei

Stellt man die Messwerte aus Material 1 Abb. 2 logarithmisch mit deren Messunsicherheiten wie in Abb. 3 dar, liegen diese näherungsweise auf einer Geraden mit der Steigung $Formula: -\mu.$ $Formula: -\mu.$

Logarithmische Darstellung von Messwerten

Abb. 3

Material 3: Absorption durch verschiedene Materialien

Die mittlere Energie der $Formula: \gamma$ $Formula: \gamma$ -Quanten, die der Tochterkern von $Formula: ^{192}\text{Ir}$ $Formula: ^{192}\text{Ir}$ aussendet, beträgt $Formula: 0,37\;\text{MeV}.$ $Formula: 0,37\;\text{MeV}.$ Abb. 4 zeigt die Absorptionskurve für solche $Formula: \gamma$ $Formula: \gamma$ -Quanten in Wasser.

Absorptionskurve für Gammaquanten in Wasser

Abb. 4: Absorptionskurve für Wasser

Wird das Experiment aus Material 1 mit anderen Materialien durchgeführt, so ergeben sich für den Schwächungskoeffizienten die in der Tabelle dargestellten Werte.

Material	$Formula: \boldsymbol{\mu}$ $Formula: \boldsymbol{\mu}$ in $Formula: \boldsymbol{\tfrac{1}{\text{cm}}}$ $Formula: \boldsymbol{\tfrac{1}{\text{cm}}}$
Aluminium
Blei
Eisen
Graphit
Wasser

Material 4: Brachytherapie

Die vom Tochterkern von $Formula: ^{192}\text{Ir}$ $Formula: ^{192}\text{Ir}$ ausgesandten $Formula: \gamma$ $Formula: \gamma$ -Quanten werden in der Medizin bei der sogenannten Brachytherapie zur Bestrahlung von Tumoren eingesetzt. Dabei wird unter Narkose eine dünne Hohlnadel in den Tumor eingebracht. In diese Hohlnadel wird eine an einem Draht befestigte winzige Kapsel hineingeschoben, in der das radioaktive Material eingeschlossen ist. So wird der Tumor direkt von innen mit den $Formula: \gamma$ $Formula: \gamma$ -Quanten bestrahlt.

Die beim Zerfall von $Formula: ^{192}\text{Ir}$ $Formula: ^{192}\text{Ir}$ entstehende $Formula: \beta^-$ $Formula: \beta^-$ -Strahlung wird durch die Umhüllung des Strahlers vollständig absorbiert, sodass diese für die Bestrahlung keine Rolle spielt.

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?

Die Zerfallsgleichung lautet:

$Formula: _{77}^{192}\mathrm{Ir} \rightarrow{ }_{78}^{192} \mathrm{Pt}+{ }_{-1}^0 \mathrm{e}+{ }_0^0 \overline{\mathrm{v}}$ $Formula: _{77}^{192}\mathrm{Ir} \rightarrow{ }_{78}^{192} \mathrm{Pt}+{ }_{-1}^0 \mathrm{e}+{ }_0^0 \overline{\mathrm{v}}$

Energiebilanz (Ir-Masse: angegeben; Pt-Masse: siehe Formelsammlung):

$Formula: \begin{array}[t]{rll} Q&=& \left[m_{\mathrm{Ir} 192}-m_{\mathrm{Pt} 192}\right] \cdot c^2 \\[5pt] &=& [191,962602-191,961043]\;\mathrm{u} \cdot c^2 \\[5pt] &=& 0,001559 \cdot 931,49\;\mathrm{MeV} \\[5pt] &=&1,45\;\mathrm{MeV} \end{array}$ $Formula: \begin{array}[t]{rll} Q&=& \left[m_{\mathrm{Ir} 192}-m_{\mathrm{Pt} 192}\right] \cdot c^2 \\[5pt] &=& [191,962602-191,961043]\;\mathrm{u} \cdot c^2 \\[5pt] &=& 0,001559 \cdot 931,49\;\mathrm{MeV} \\[5pt] &=&1,45\;\mathrm{MeV} \end{array}$

Verteilung der kinetischen Energie der $Formula: \beta^{-}$ $Formula: \beta^{-}$ -Teilchen:

Es ergibt sich ein kontinuierliches Betaspektrum.
Da der -Wert die freiwerdende Energie des Betazerfalls beschreibt, markiert er auf der Energieachse den rechten Rand der Kurve (= maximale Energie).

Der Abstand Formula: s muss konstant gehalten werden, weil das Präparat nicht nur entlang der Symmetrieachse der Anordnung strahlt, sondern ein gewisses Winkelfeld bestrahlt. Würde beispielsweise größer, würden nicht mehr so viele Betateilchen das Zählrohr treffen und die Messung der Zählrate verfälscht werden.

Halbwertsdicke von Blei

Als Ausgangsanzahl wird der Wert $Formula: N_0=N(0\;\mathrm{cm})=800$ $Formula: N_0=N(0\;\mathrm{cm})=800$ abgelesen.

Für die Dicke, die zum halben Wert $Formula: \tfrac{N_0}{2}=400$ $Formula: \tfrac{N_0}{2}=400$ gehört, ergibt sich mit der Abbildung:

$Formula: D_{\tfrac{1}{2}}=0,27\;\mathrm{cm}$ $Formula: D_{\tfrac{1}{2}}=0,27\;\mathrm{cm}$

$Formula: D_\tfrac{1}{2}=\dfrac{\ln 2}{\mu}$ Kombinieren des in Material 1 angegebene Abnahmegesetz $Formula: N(d)=N_0 \cdot \mathrm{e}^{-\mu \cdot d}$ $Formula: N(d)=N_0 \cdot \mathrm{e}^{-\mu \cdot d}$ mit der Definition der Halbwertsdicke $Formula: N\left(D_{\tfrac{1}{2}}\right)=\tfrac{1}{2}\;N_0$ $Formula: N\left(D_{\tfrac{1}{2}}\right)=\tfrac{1}{2}\;N_0$ und Umstellen liefert:

$Formula: \begin{array}{ll} \left.\begin{array}{l} N\left(D_{\tfrac{1}{2}}\right)=N_0 \cdot \mathrm e^{-\mu \cdot D_{\tfrac{1}{2}}} \\ N\left(D_{\tfrac{1}{2}}\right)=\dfrac{1}{2} N_0 \end{array}\right\} \Rightarrow & \mathrm e^{-\mu \cdot D_{\tfrac{1}{2}}}=\dfrac{1}{2} \\ & -\mu \cdot D_{\tfrac{1}{2}}=\ln \left(\dfrac{1}{2}\right) \\ & \mu \cdot D_{\tfrac{1}{2}}=\ln 2 \Rightarrow D_{\tfrac{1}{2}}=\dfrac{\ln 2}{\mu} \end{array}$ $Formula: \begin{array}{ll} \left.\begin{array}{l} N\left(D_{\tfrac{1}{2}}\right)=N_0 \cdot \mathrm e^{-\mu \cdot D_{\tfrac{1}{2}}} \\ N\left(D_{\tfrac{1}{2}}\right)=\dfrac{1}{2} N_0 \end{array}\right\} \Rightarrow & \mathrm e^{-\mu \cdot D_{\tfrac{1}{2}}}=\dfrac{1}{2} \\ & -\mu \cdot D_{\tfrac{1}{2}}=\ln \left(\dfrac{1}{2}\right) \\ & \mu \cdot D_{\tfrac{1}{2}}=\ln 2 \Rightarrow D_{\tfrac{1}{2}}=\dfrac{\ln 2}{\mu} \end{array}$

Bestimmung von $Formula: \boldsymbol{\mu}$ $Formula: \boldsymbol{\mu}$

Bestimmen des im Rahmen der Messunsicherheiten minimalen bzw. maximalen Wert von $Formula: \mu$ $Formula: \mu$ mithilfe von zwei Steigungsdreiecken, indem durch die oberen bzw. unteren Messfehlergrenzen eine Gerade gelegt wird, liefert:

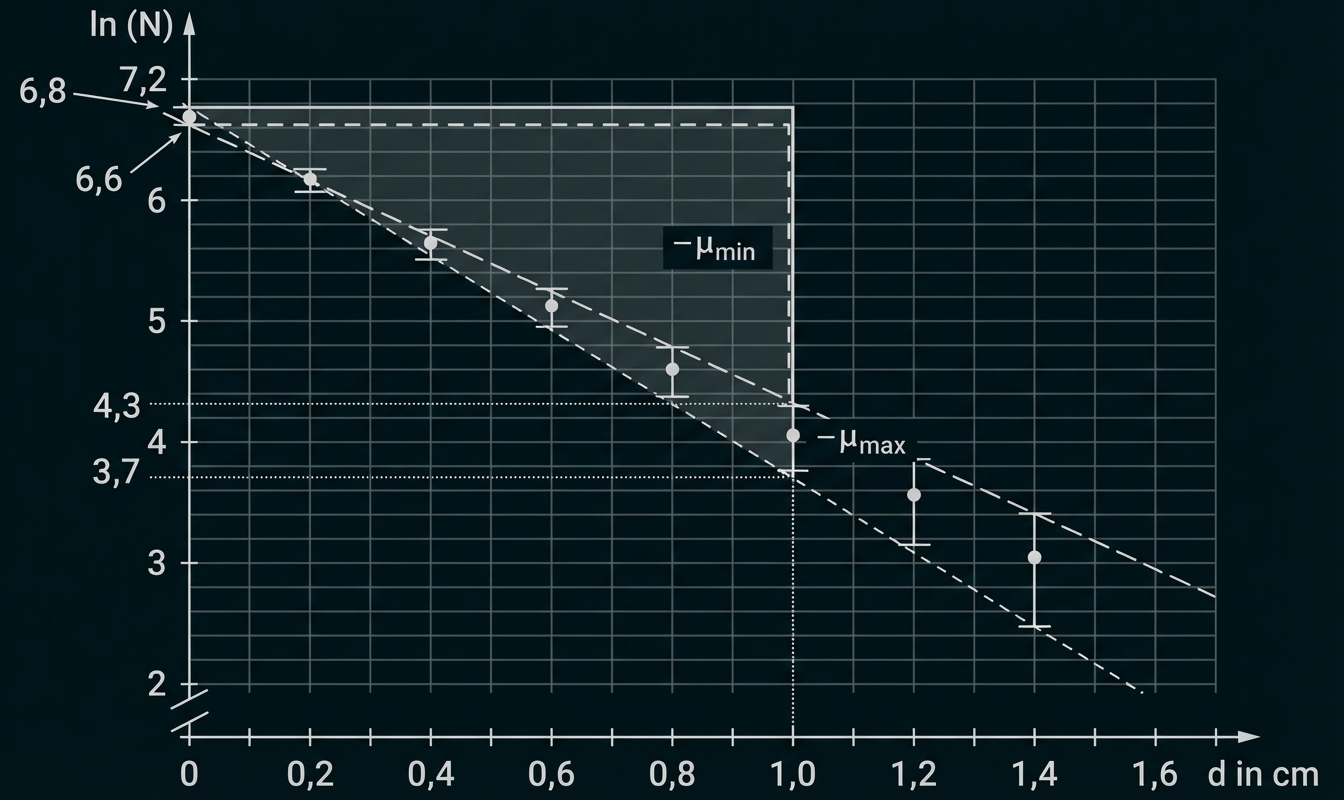
Graphische Bestimmung des minimalen und maximalen Schwächungskoeffizienten mit Steigungsdreiecken

Es ergibt sich:

$Formula: -\mu_{\min}=\dfrac{{\Delta(\ln N)}_{\min}}{\Delta d}=\dfrac{4,3-6,6}{1,0\;\mathrm{cm}}$ $Formula: -\mu_{\min}=\dfrac{{\Delta(\ln N)}_{\min}}{\Delta d}=\dfrac{4,3-6,6}{1,0\;\mathrm{cm}}$ $Formula: =-2,3\;\frac{1}{\mathrm{cm}} \Rightarrow \mu_{\min }=2,3\;\dfrac{1}{\mathrm{cm}}$ $Formula: =-2,3\;\frac{1}{\mathrm{cm}} \Rightarrow \mu_{\min }=2,3\;\dfrac{1}{\mathrm{cm}}$

$Formula: -\mu_{\max}=\dfrac{{\Delta(\ln N)}_{\max }}{\Delta d}=\dfrac{3,7-6,8}{1,0\;\mathrm{cm}}$ $Formula: -\mu_{\max}=\dfrac{{\Delta(\ln N)}_{\max }}{\Delta d}=\dfrac{3,7-6,8}{1,0\;\mathrm{cm}}$ $Formula: =-3,1\;\dfrac{1}{\mathrm{cm}} \Rightarrow \mu_{\max}=3,1\;\frac{1}{\mathrm{cm}}$ $Formula: =-3,1\;\dfrac{1}{\mathrm{cm}} \Rightarrow \mu_{\max}=3,1\;\frac{1}{\mathrm{cm}}$

Als Messwert folgt durch Bildung des arithmetischen Mittels

$Formula: \mu=\dfrac{\mu_{\min }+\mu_{\max }}{2}=\dfrac{2,3+3,1}{2}\;\frac{1}{\mathrm{cm}}$ $Formula: \mu=\dfrac{\mu_{\min }+\mu_{\max }}{2}=\dfrac{2,3+3,1}{2}\;\frac{1}{\mathrm{cm}}$ $Formula: =2,7\;\frac{1}{\mathrm{cm}}$ $Formula: =2,7\;\frac{1}{\mathrm{cm}}$

und schließlich unter Berücksichtigung der Abweichungen zu $Formula: \mu_{\min }$ $Formula: \mu_{\min }$ und $Formula: \mu_{\max }:$ $Formula: \mu_{\max }:$

$Formula: \mu=(2,7 \pm 0,4)\;\frac{1}{\mathrm{~cm}}$ $Formula: \mu=(2,7 \pm 0,4)\;\frac{1}{\mathrm{~cm}}$

Bestimmung der Halbwertsdicke

Zunächst ergibt sich durch Einsetzen:

$Formula: D_{\tfrac{1}{2}}=\dfrac{\ln 2}{\mu}=\dfrac{\ln 2}{2,7\;\mathrm{cm}^{-1}}=0,26\;\mathrm{cm}$ $Formula: D_{\tfrac{1}{2}}=\dfrac{\ln 2}{\mu}=\dfrac{\ln 2}{2,7\;\mathrm{cm}^{-1}}=0,26\;\mathrm{cm}$

Für die Fehlerbetrachtung darf eine lineare Fehlerfortpflanzung angenommen werden. Man erhält

$Formula: \frac{\Delta \mu}{\mu} =\frac{\Delta D_{\tfrac{1}{2}}}{D_{\tfrac{1}{2}}}$ $Formula: \frac{\Delta \mu}{\mu} =\frac{\Delta D_{\tfrac{1}{2}}}{D_{\tfrac{1}{2}}}$

$Formula: \Rightarrow \begin{array}[t]{rll} \Delta D_{\tfrac{1}{2}}&=& D_{\tfrac{1}{2}} \cdot \frac{\Delta \mu}{\mu} \\[5pt] &=& 0,26\;\mathrm{cm} \cdot \frac{0,4\;\mathrm{cm}^{-1}}{2,7\;\mathrm{cm}^{-1}} \\[5pt] &=&0,04\;\mathrm{cm}\end{array}$ $Formula: \Rightarrow \begin{array}[t]{rll} \Delta D_{\tfrac{1}{2}}&=& D_{\tfrac{1}{2}} \cdot \frac{\Delta \mu}{\mu} \\[5pt] &=& 0,26\;\mathrm{cm} \cdot \frac{0,4\;\mathrm{cm}^{-1}}{2,7\;\mathrm{cm}^{-1}} \\[5pt] &=&0,04\;\mathrm{cm}\end{array}$

und damit:

$Formula: \mathrm{D}_{\tfrac{1}{2}}=(0,26 \pm 0,4)\;\mathrm{cm}$ $Formula: \mathrm{D}_{\tfrac{1}{2}}=(0,26 \pm 0,4)\;\mathrm{cm}$

Der in Teilaufgabe c abgelesene Wert von $Formula: 0,27\;\mathrm{cm}$ $Formula: 0,27\;\mathrm{cm}$ stimmt im Rahmen der Messunsicherheiten gut mit diesem Wert überein.

Der menschliche Körper besteht zum großen Teil aus Wasser, weswegen die Absorptionskurve für Wasser näherungsweise auch für menschliches Gewebe verwendet werden kann.

Blei hat laut der Tabelle in Material 3 den mit Abstand größten Schwächungskoeffizienten der aufgelisteten Materialien. Es eignet sich daher am besten für die Verwendung in Schutzkleidung, weil die gleiche Abschwächungswirkung mit deutlich dünneren – und damit leichter und bequemer tragbaren – Kleidungsschichten erzielt wird.

Nach exakt $Formula: 48\;\mathrm{h}=2\;\mathrm{d}$ $Formula: 48\;\mathrm{h}=2\;\mathrm{d}$ beträgt die Aktivität zum Zeitpunkt der Bestrahlung

$Formula: \begin{array}[t]{rll} A(2\;\mathrm{d})&=& A_0 \cdot\left(\dfrac{1}{2}\right)^{\tfrac{2\;\mathrm{d}}{T_{\tfrac{1}{2}}}} \\[5pt] &=& 220\;\mathrm{GBq} \cdot\left(\dfrac{1}{2}\right)^{\tfrac{2 \;\mathrm{d}}{73,8\;\mathrm{d}}} \\[5pt] &=&216\;\mathrm{GBq}\end{array}$ $Formula: \begin{array}[t]{rll} A(2\;\mathrm{d})&=& A_0 \cdot\left(\dfrac{1}{2}\right)^{\tfrac{2\;\mathrm{d}}{T_{\tfrac{1}{2}}}} \\[5pt] &=& 220\;\mathrm{GBq} \cdot\left(\dfrac{1}{2}\right)^{\tfrac{2 \;\mathrm{d}}{73,8\;\mathrm{d}}} \\[5pt] &=&216\;\mathrm{GBq}\end{array}$

Die festgelegte Energiedosis bleibt bei verringerter Aktivität konstant, wenn die Bestrahlungszeit Formula: t entsprechend der Gleichung

$Formula: A_0 \cdot t_0=A(2\;\mathrm{d}) \cdot t$ $Formula: A_0 \cdot t_0=A(2\;\mathrm{d}) \cdot t$

erhöht wird. Durch Umstellen folgt:

$Formula: t=\dfrac{A_0}{A(2\;\mathrm{d})} \cdot t_0=\dfrac{220\;\mathrm{GBq}}{216\;\mathrm{GBq}} \cdot 720\;\mathrm{s}=734\;\mathrm{s}$ $Formula: t=\dfrac{A_0}{A(2\;\mathrm{d})} \cdot t_0=\dfrac{220\;\mathrm{GBq}}{216\;\mathrm{GBq}} \cdot 720\;\mathrm{s}=734\;\mathrm{s}$

Die Äquivalentdosis berechnet wird mit der Formel

$Formula: H=q \cdot \frac{E}{m}$ $Formula: H=q \cdot \frac{E}{m}$

berechnet. Für die auftretenden Größen gilt:

biologischer Bewertungsfaktor: für Gammastrahlung
Masse des Tumors: $Formula: m=120\;\text{g}$ $Formula: m=120\;\text{g}$
In der Zeit eingestrahlte Energie Gemäß Abb. 4 gelangen bei einer Schichtdicke von $Formula: 3,0\;\mathrm{cm}$ $Formula: 3,0\;\mathrm{cm}$ rund $Formula: 70\,\%$ $Formula: 70\,\%$ der Gammaquanten nach außen, d.h., rund $Formula: 30\,\%$ $Formula: 30\,\%$ werden absorbiert. Die Energie eines Gammaquants beträgt laut Material 3 im Mittel $Formula: 0,37\;\mathrm{MeV},$ $Formula: 0,37\;\mathrm{MeV},$ die Gesamtzahl der freigesetzten Gammaquanten beträgt $Formula: N=A_0 \cdot t_0.$ $Formula: N=A_0 \cdot t_0.$ Damit ergibt sich $Formula: E=0,30 \cdot 0,37\;\mathrm{MeV}$ $Formula: E=0,30 \cdot 0,37\;\mathrm{MeV}$ $Formula: \cdot 220 \;\mathrm{GBq} \cdot 720\;\mathrm{s}.$ $Formula: \cdot 220 \;\mathrm{GBq} \cdot 720\;\mathrm{s}.$

Für die Äquivalentdosis ergibt sich:

$Formula: H=1 \cdot \frac{0,30 \cdot 0,37 \cdot 10^6 \cdot 1,6 \cdot 10^{-19}\;\mathrm{J} \cdot 220 \cdot 10^9\;\mathrm{Bq} \cdot 720\;\mathrm{s}}{0,120\;\mathrm{kg}}=23\;\mathrm{Sv}$ $Formula: H=1 \cdot \frac{0,30 \cdot 0,37 \cdot 10^6 \cdot 1,6 \cdot 10^{-19}\;\mathrm{J} \cdot 220 \cdot 10^9\;\mathrm{Bq} \cdot 720\;\mathrm{s}}{0,120\;\mathrm{kg}}=23\;\mathrm{Sv}$

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?

A4 Kernphysik Medizin

Material 1: Absorption von -Strahlung durch Materie

Material 2: Schwächungskoeffizient von Blei

Material 3: Absorption durch verschiedene Materialien

Material 4: Brachytherapie

Weiter lernen mit SchulLV-PLUS!

Weiter lernen mit SchulLV-PLUS!

Material 1: Absorption von $Formula: \color{#287882}{\boldsymbol{\gamma}}$ $Formula: \color{#287882}{\boldsymbol{\gamma}}$ -Strahlung durch Materie