Analysis 2.1 – Windrad

Gegeben ist die in $\mathbb{R}$ definierte Funktion $f$ mit $f(x)=\frac{2}{25} x^3-\frac{3}{2} x.$

Der Graph von $f$ heißt $G_f.$

Weise nach, dass der Graph $G_f$ punktsymmetrisch zum Koordinatenursprung ist.

Bestimme die Nullstellen von $f.$

(5 BE)

Der Graph $G_f$ hat genau zwei Extrempunkte.

Bestimme die Koordinaten dieser Extrempunkte.

Zeige, dass die Gerade durch die Extrempunkte von $G_f$ die Winkelhalbierende des $\text{II}.$ und $\text{IV}.$ Quadranten ist.

(7 BE)

In einem Malbuch für Kinder wird ein Windrad abgebildet. Zur Modellierung zweier Flügel dieses Windrades werden der Graph $G_f$ und die Gerade $g$ mit $g(x)=\frac{1}{2}x$ im Intervall $\left[-5;5\right]$ verwendet. Dreht man diese beiden Flügel um $90^{\circ}$ gegen den Uhrzeigersinn um den Koordinatenursprung, so erhält man die anderen beiden Flügel (siehe Abbildung). Die durch die Drehung der Geraden $g$ entstandene Gerade heißt $g^*,$ die Endpunkte der Flügel auf dieser Geraden heißen $A^*$ bzw. $B^*.$ Der Punkt $A(5 \mid 2,5)$ ist der Schnittpunkt von $G_f$ mit $g$ und liegt auf dem abgebildeten Kreis.

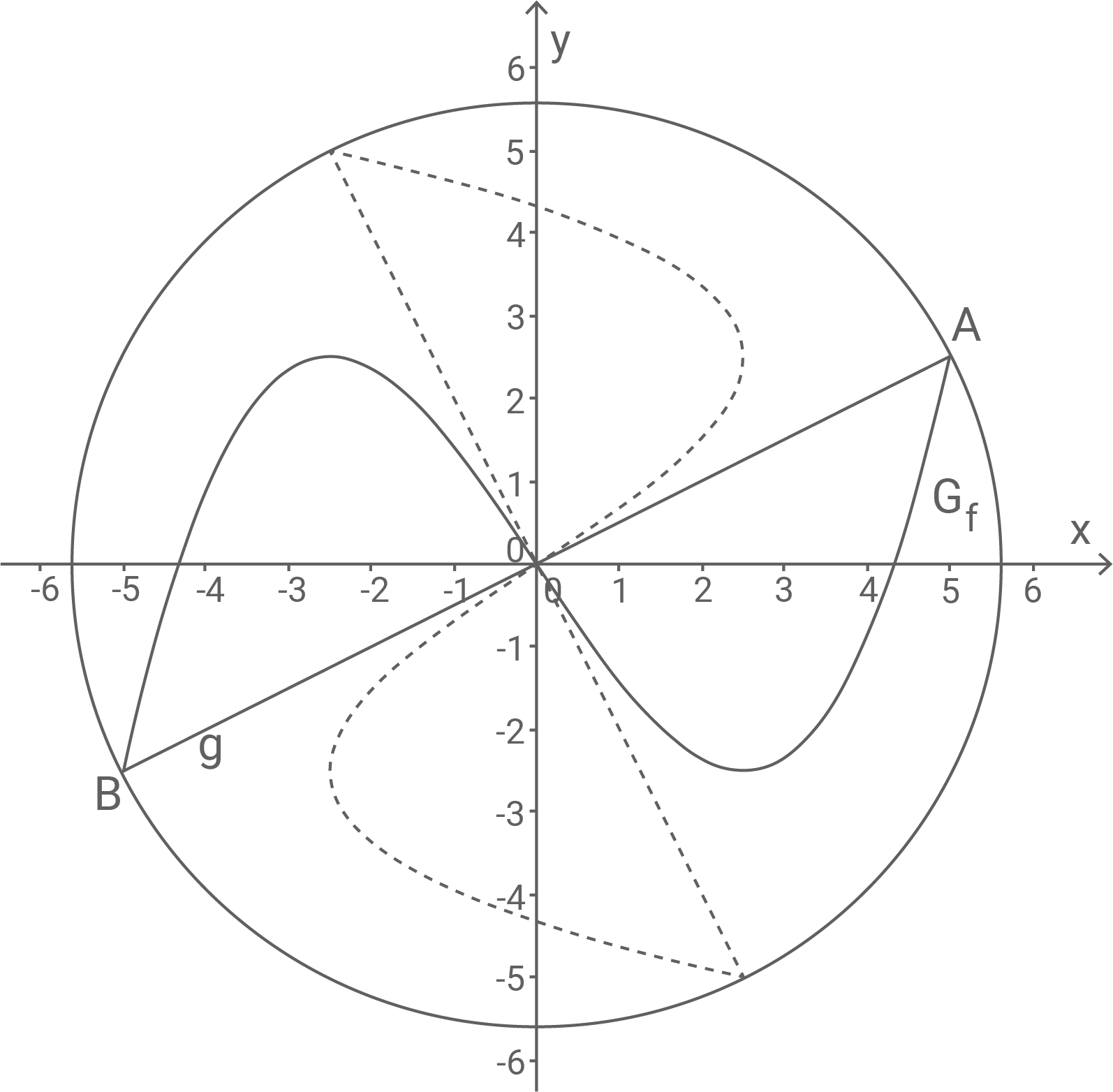
Abbildung

Begründe, dass für $g^*$ gilt: $g^*(x)=-2 x.$

Der Punkt $A^*$ geht durch die Drehung aus dem Punkt $A$ hervor.

Gib die Koordinaten des Punktes $A^*$ an.

(3 BE)

Betrachtet wird die Tangente $k$ an $G_f$ im Punkt $\left(\frac{5\sqrt{3}}{2} \mid 0 \right).$

Bestimme den Steigungswinkel der Tangente $k.$

Untersuche, ob die folgende Aussage wahr ist:

Für den Schnittwinkel $\alpha$ von $k$ und $g$ gilt: $\sin (\alpha)=\cos (\alpha).$

(5 BE)

Im Zusammenhang mit dem Windrad gibt es zwei Flächen: $A_1$ und $A_2.$

Für den Inhalt der Fläche $A_1$ gilt: $A_1=\left(\frac{5 \sqrt{5}}{2}\right)^2 \cdot\pi.$
Der Inhalt der Fläche $A_2$ kann mit der Gleichung $A_2=4 \cdot \displaystyle\int_0^5(g(x)-f(x)) \;\mathrm{d} x$ berechnet werden.

Veranschauliche die Fläche $A_1-A_2$ in der Abbildung.

Berechne den Inhalt der Fläche $A_1-A_2.$

(5 BE)

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?

Punktsymmetrie des Graphen $\boldsymbol{G_f}$ nachweisen

$\begin{array}[t]{rlll} f(-x) &=& \dfrac{2}{25}\cdot(-x)^3-\dfrac{3}{2} \cdot(-x) \\[5pt] &=& -\dfrac{2}{25} x^3+\dfrac{3}{2} x \\[5pt] &=& -f(x) \end{array}$

Der Graph $G_f$ ist punktsymmetrisch zum Koordinatenursprung, da $f(-x)=-f(x).$

Nullstellen von $\boldsymbol{f(x)}$ bestimmen

$\begin{array}[t]{rlll} f(x) &=& 0 \\[5pt] \dfrac{2}{25}x^3-\dfrac{3}{2}x &=& 0 \\[5pt] x\cdot \left(\dfrac{2}{25}x^2-\dfrac{3}{2}\right) &=& 0 \\[5pt] \end{array}$

Mit dem Satz des Nullprodukts folgt $x_1=0$ und weiter:

$\begin{array}[t]{rlll} \dfrac{2}{25}x^2-\dfrac{3}{2} &=& 0 &\mid\; + \dfrac{3}{2} \\[5pt] \dfrac{2}{25}x^2 &=& \dfrac{3}{2} &\mid\; : \dfrac{2}{25} \\[5pt] x^2 &=& \dfrac{75}{4} &\mid\; \sqrt{\;} \\[5pt] x_2 &=& -\dfrac{5 \sqrt{3}}{2} \\[5pt] x_3 &=& \dfrac{5 \sqrt{3}}{2} \end{array}$

Extrempunkte bestimmen

Erste Ableitung $\(\boldsymbol{f$ aufstellen

$\(f$

Ableitung gleich null setzen

$\(\begin{array}[t]{rlll} f$

Hierbei muss die hinreichende Bedingung $\(f$ nicht bestimmt werden, da im Aufgabentext steht, dass der Graph $G_f$ genau zwei Extremstellen hat.

$\boldsymbol{y}$ -Koordinate des ersten Extrempunkts berechnen

$\begin{array}[t]{rlll} f\left(\dfrac{5}{2}\right) &=& \dfrac{2}{25} x^3-\dfrac{3}{2} x \\[5pt] &=& -\dfrac{5}{2} \end{array}$

$\boldsymbol{y}$ -Koordinate des zweiten Extrempunkts berechnen

$\begin{array}[t]{rlll} f\left(-\dfrac{5}{2}\right) &=& \dfrac{2}{25} x^3-\dfrac{3}{2} x \\[5pt] &=& \dfrac{5}{2} \end{array}$

Somit folgt für die Extrempunkte $E_1\left(\dfrac{5}{2} \left\lvert\,-\dfrac{5}{2}\right.\right)$ und $E_2 \left(-\dfrac{5}{2} \left\lvert\, \dfrac{5}{2}\right.\right).$

Gerade durch die Extrempunkte betrachten

Die Gerade durch $E_1$ und $E_2$ hat folgende Steigung:

$\begin{array}[t]{rlll} m &=& \dfrac{y_2-y_1}{x_2-x_1} \\[5pt] &=& \dfrac{\frac{5}{2}-\left(-\frac{5}{2}\right)}{-\frac{5}{2}-\frac{5}{2}} \\[5pt] &=& -1 \end{array}$

Geradengleichung bestimmen

$\begin{array}[t]{rlll} y &=& mx+n \\[5pt] -\dfrac{5}{2} &=& -1 \cdot \dfrac{5}{2}+n &\mid\; +\dfrac{5}{2} \\[5pt] 0 &=& n \end{array}$

Die Geradengleichung lautet $y = -x$ und ist somit die Winkelhalbierende des $\text{II}.$ und $\text{IV}.$ Quadranten.

Begründen, dass $\boldsymbol{g^*(x)=-2 x}$ ist

Die Gerade $g^*$ entsteht durch Drehung von $g$ um $90^{\circ}$ gegen den Uhrzeigersinn um den Ursprung.
Eine Gerade, die bei $90^{\circ}$ -Drehung um den Ursprung entsteht, ist orthogonal zur ursprünglichen Gerade $g.$ Steigung von $g:$

$m=\dfrac{1}{2}$

Dann ist die Steigung der orthogonalen Gerade:

$m^*=-\dfrac{1}{m}=-2$

Da der Ursprung $(0 \mid 0)$ sowohl auf $g$ als auch auf $g^*$ liegt, gilt:

$g^*(x)=-2 x$

Koordinaten des Punktes $\boldsymbol{A^*}$ angeben

$A=(-2,5 \mid 5)$

Mathematische Grafik mit Koordinatensystem, Linien und Winkeln, die verschiedene Funktionen darstellen.

Hilfsskizze

Steigung der Tangenten $\boldsymbol{k}$ bestimmen

$\(\begin{array}[t]{rlll} f$

Steigungswinkel der Tangente $\boldsymbol{k}$ berechnen

$\begin{array}[t]{rlll} \tan(\beta) &=& 3 \\[5pt] \beta &\approx& 71,6^\circ \end{array}$

Steigung der Geraden $g: m=\dfrac{1}{2}$

Steigungswinkel der Geraden $g$ berechnen

$\begin{array}[t]{rlll} \tan(\gamma) &=& \dfrac{1}{2} \\[5pt] \gamma &\approx& 26,6^\circ \end{array}$

Schnittwinkel zwischen $\boldsymbol{k}$ und $\boldsymbol{g}$ berechnen

Der Innenwinkel am Schnittpunkt der $x$ -Achse und $k$ beträgt $180^\circ-\beta.$

Die Innenwinkelsumme des Dreiecks, das durch $k,g$ und die $x$ -Achse begrenzt wird, beträgt $180^\circ.$

Um $\alpha$ auszurechnen, wird die Innenwinkelsumme mit $\alpha, \gamma$ und $180^\circ-\beta$ gleichgestellt und anschließend nach $\alpha$ umgeformt.

$\begin{array}[t]{rlll} 180^\circ &=& \alpha+\gamma+180^\circ-\beta \\[5pt] 180^\circ &=& \alpha+ 26,6^\circ+180^\circ-71,6^\circ\\[5pt] 180^\circ &=& \alpha+135^\circ &\mid\; -135^\circ\\[5pt] 45^\circ &=& \alpha \end{array}$

Es gilt: $\sin \left(45^{\circ}\right)=\cos \left(45^{\circ}\right).$ Also ist die Aussage wahr.

Radius des Kreises $\boldsymbol{r}$ berechnen

$\begin{array}[t]{rlll} r &=& \overline{OA} \\[5pt] &=& \sqrt{5^2+2,5^2} \\[5pt] &=& \dfrac{5\cdot\sqrt{5}}{2} \end{array}$

Graph einer Funktion im kartesischen Koordinatensystem mit einer kreisförmigen Darstellung.

Inhalt der Fläche $\boldsymbol{A_2}$ berechnen

$\begin{array}[t]{rlll} A_2 &=& 4 \cdot \displaystyle\int_0^5(g(x)-f(x))\;\text{d} x \\[5pt] &=& 4 \cdot \displaystyle\int_0^5\left(\frac{1}{2} x-\left(\frac{2}{25} x^3-\frac{3}{2} x\right)\right)\;\text{d} x \\[5pt] &=& 4 \cdot\displaystyle\int_0^5\left(-\frac{2}{25} x^3+2 x\right) \;\text{d}x \\[5pt] &=& 4 \cdot\left[-\dfrac{1}{50} x^4+x^2\right]_0^5 \\[5pt] &=& 4 \cdot \left(-\dfrac{1}{50} 5^4+5^2\right)-\left(-\dfrac{1}{50} 0^4+0^2\right) \\[5pt] &=& 50 \end{array}$

Inhalt der Fläche $\boldsymbol{A_1-A_2}$ berechnen

Der Inhalt der Fläche des ganzen Kreises $A_1$ beträgt $\left(\dfrac{5 \sqrt{5}}{2}\right)^2 \cdot \pi.$

$\begin{array}[t]{rlll} A_1-A_2 &=& \left(\dfrac{5 \sqrt{5}}{2}\right)^2 \cdot \pi - 50 \\[5pt] &\approx& 48,17 \end{array}$

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?