Wahlaufgaben

1.4.1 Analysis

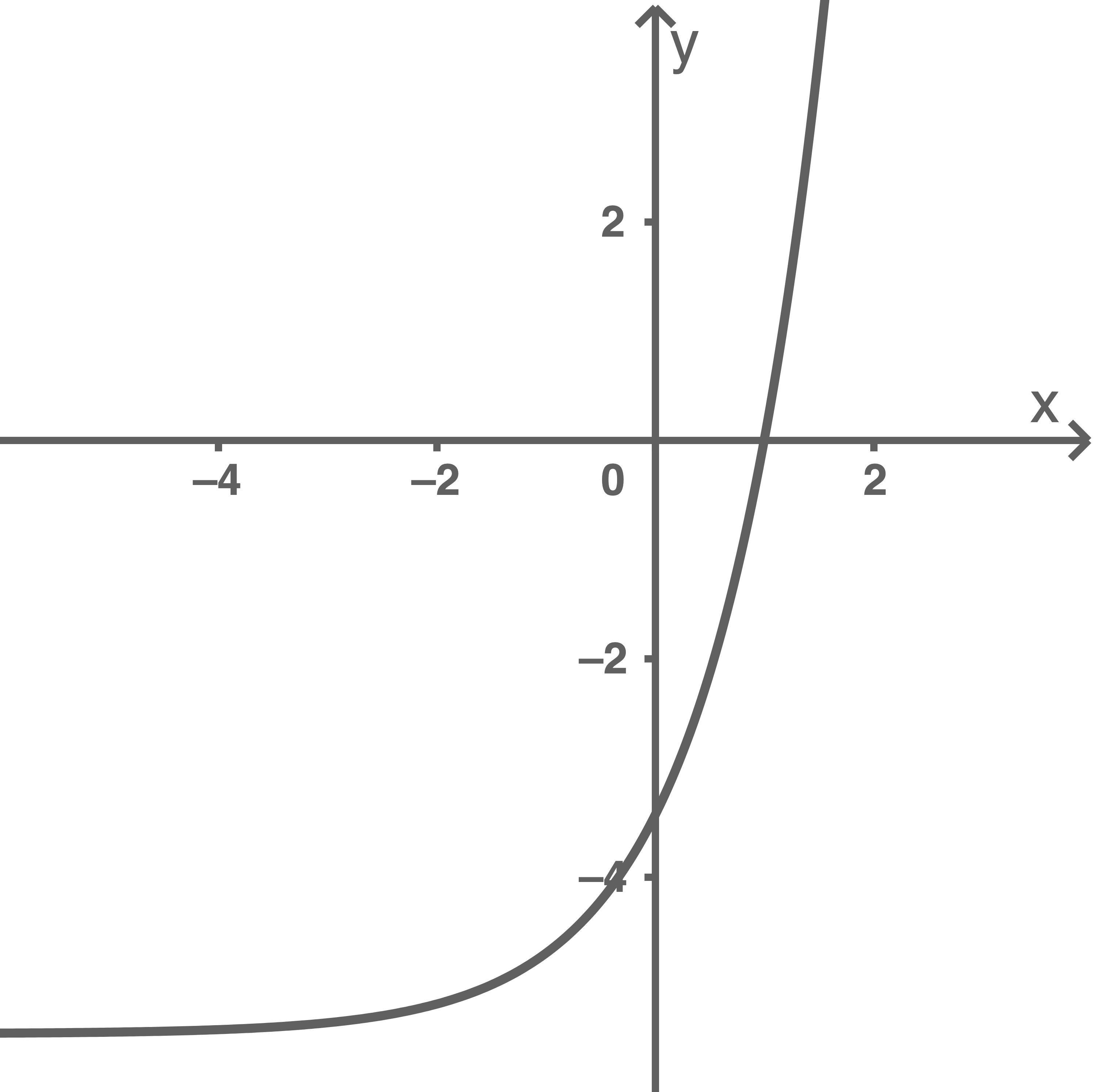
Die Abbildung zeigt den Graphen der in $\mathbb{R}$ definierten Funktion $f$ mit $f(x)=2 \text{e}^x-2 \text{e}.$

Weise nach, dass $1$ eine Nullstelle von $f$ ist.

(1 BE)

Der Graph von $f$ schließt mit den Koordinatenachsen eine Fläche ein.

Berechne ihren Inhalt.

(4 BE)

Abbildung

1.4.2 Analytische Geometrie

Gegeben sind die Punkte $P(0\mid -1\mid 1)$ und $Q(2\mid 5\mid 3).$

Durch Spiegelung des Punktes $P$ am Punkt $Q$ entsteht der Punkt $\(P$

Ermittle die Koordinaten von $\(P$

(2 BE)

Die Ebene E hat die Gleichung $E: x_1+3 x_2+x_3=20.$

Weise nach, dass $Q$ in $E$ liegt und der Vektor $\overrightarrow{P Q}$ ein Normalenvektor von $E$ ist.

(3 BE)

1.4.3 Stochastik

In einer Schwimmgruppe, zu der $20$ Kinder gehören, haben $9$ Kinder das Schwimmabzeichen Bronze.

Zwei Kinder der Schwimmgruppe werden zufällig ausgewählt.

Berechne die Wahrscheinlichkeit dafür, dass diese beiden Kinder das Schwimmabzeichen Bronze haben.

(2 BE)

Gib die Bedeutung des folgenden Terms im Sachzusammenhang an:

$\dfrac{\binom{9}{2} \cdot\binom{11}{4}}{\binom{20}{6}}$

(3 BE)

1.5.1 Analysis

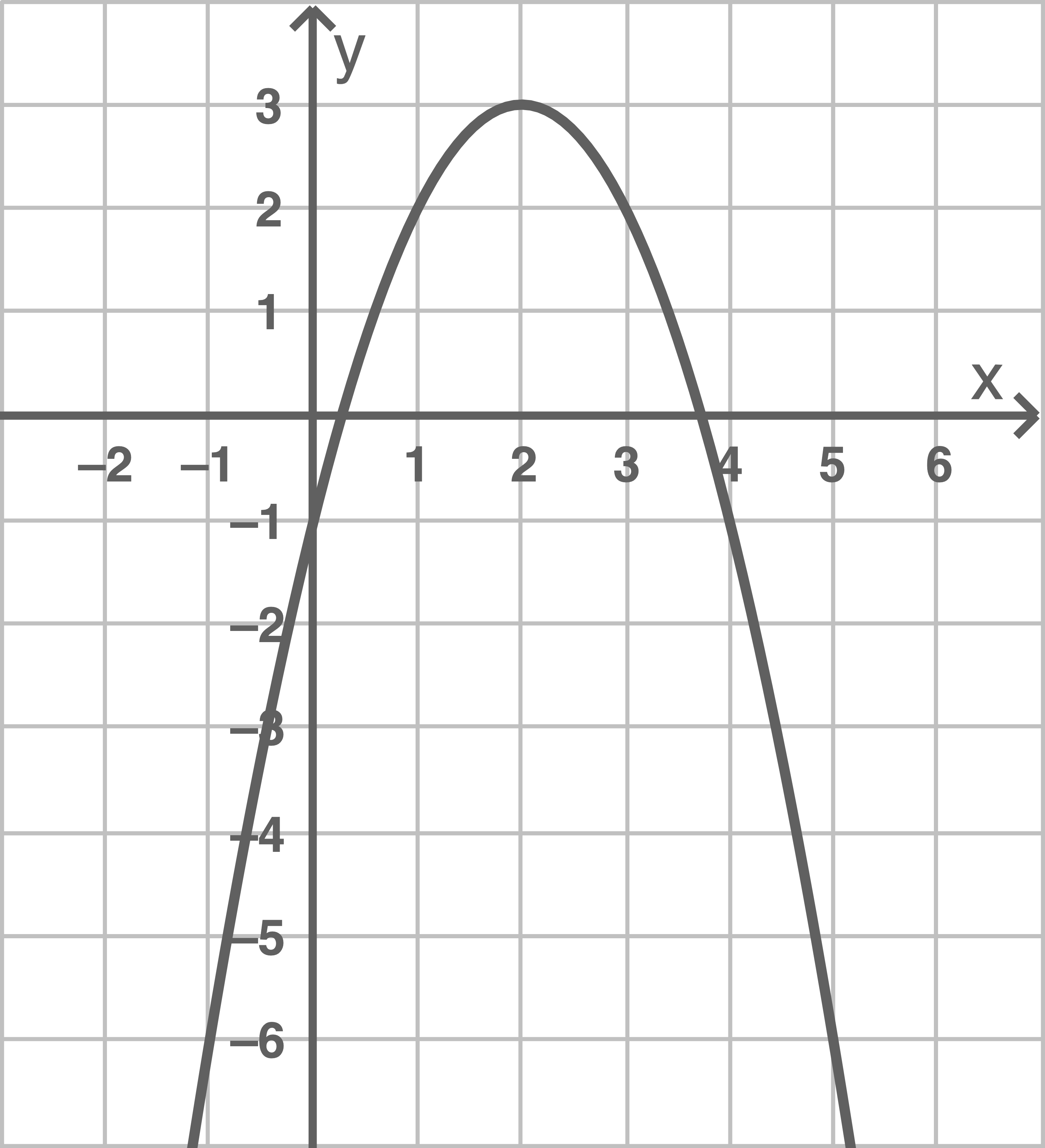
Die Abbildung zeigt den Graphen der in $\mathbb{R}$ definierten Funktion $f$ mit $f(x)=-x^2+4 x-1.$

Betrachtet wird die Gleichung $\(\dfrac{f(x)-0}{x-0}=f$

Gib einen Term der ersten Ableitungsfunktion $\(f$ von $f$ an und ermittle rechnerisch die Lösungen der Gleichung.

(3 BE)

Gib die geometrische Bedeutung der Gleichung an, die sich für deren Lösungen ergibt.

(2 BE)

Abbildung

1.5.2 Analytische Geometrie

Die Ebene $E$ wird durch die Gleichung $\overrightarrow{x}=\pmatrix{1\\-3\\0}+r \cdot\pmatrix{-3\\4\\1}+s \cdot \pmatrix{3\\-4\\0}$ mit $r, s \in \mathbb{R}$ beschrieben.

Zeige, dass der Vektor $\pmatrix{4\\3\\0}$ senkrecht zur Ebene $E$ steht.

(2 BE)

Bestimme die Koordinaten eines Punkts $P$ mit folgender Eigenschaft:
Wird der Punkt $P$ an der Ebene $E$ gespiegelt, so hat der entstehende Punkt vom Punkt $P$ den Abstand $20.$

(3 BE)

1.5.3 Stochastik

Die Abbildung zeigt die Wahrscheinlichkeitsverteilung einer binomialverteilten Zufallsgröße $X$ mit den Parametern $n$ und $p=0,5.$

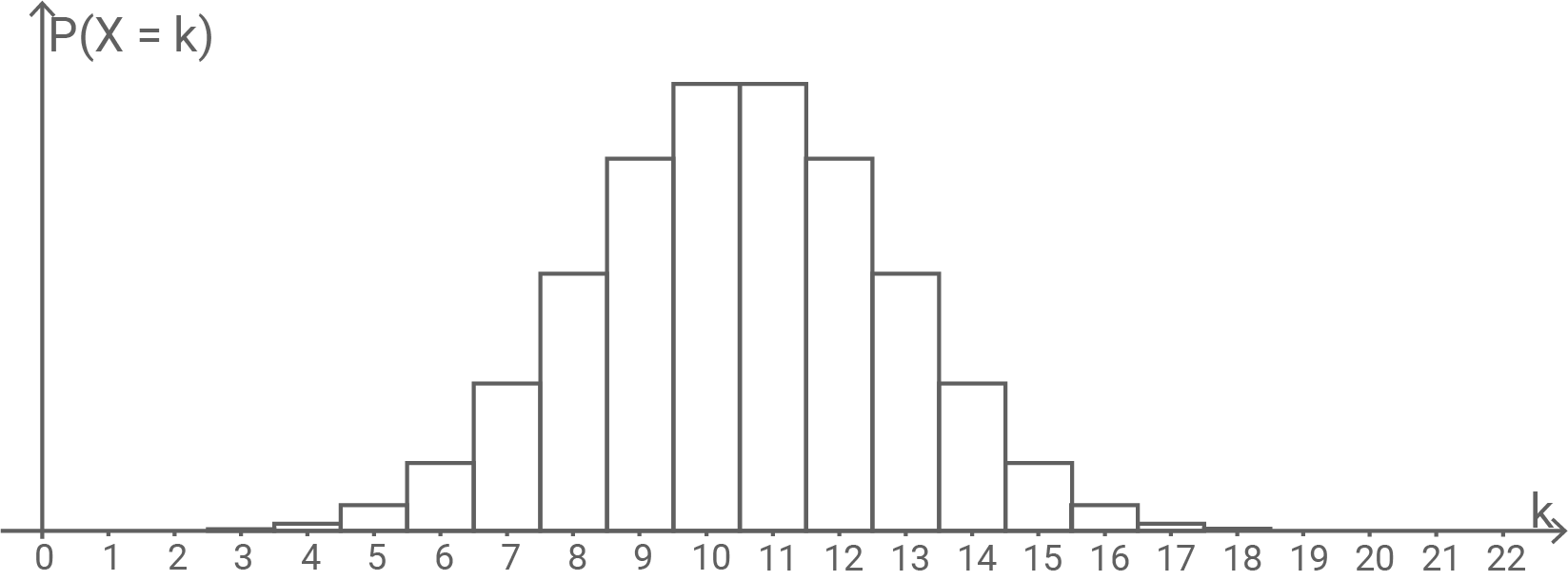
Abbildung

Es gilt $P(X=10)=P(X=11).$

Begründe, dass $n$ nicht gerade ist.

(2 BE)

Es gilt $P(X \geq 9) \approx 0,81$ und $P(X=12) \approx 0,14.$

Berechne unter Verwendung dieser Werte näherungsweise die Wahrscheinlichkeit $P(X=10).$

(3 BE)

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?

4.1

$\begin{array}[t]{rll} f(1) &=& 2 \mathrm{e}^1 -2\mathrm{e} \\[5pt] &=& 0 \end{array}$

$\boldsymbol{F(x)}$ aufstellen

$F(x) = 2\mathrm{e}^x-2\mathrm{e}x$

Integral berechnen

$\begin{array}[t]{rll} \displaystyle\int_{0}^{1}f(x)\;\mathrm dx &=& \left[ 2\text{e}^x-2\text{e}x \right]_0^1 \\[5pt] &=& 2\mathrm{e}-2\text{e}-2 \\[5pt] &=& -2 \end{array}$

Somit beträgt der Flächeninhalt $2.$

1.4.2 Analytische Geometrie

$\(\overrightarrow{OP$

Die Koordinaten von $\(P$ ergeben sich damit als $\(P$

Einsetzen der Koordinaten von $Q$ in die Ebenengleichung von $E$ liefert $2+3\cdot 5+3=20.$ Da beide Seiten übereinstimmen, liegt $Q$ somit in $E.$

$\overrightarrow{PQ}= \pmatrix{2-0\\5-(-1)\\3-1}=2\cdot\pmatrix{1\\3\\1}$

1.4.3 Stochastik

$\begin{array}[t]{rlll} p &=& \dfrac{9}{20}\cdot \dfrac{8}{19}\\[5pt] &=& \dfrac{72}{380} \end{array}$

Der Term gibt die Wahrscheinlichkeit dafür an, dass in einer zufälligen Auswahl von sechs Kindern der Schwimmgruppe zwei Kinder das Schwimmabzeichen Bronze haben.

1.5.1 Analysis

Term von $\(\boldsymbol{f$ angeben

$\(f$

Lösungen der Gleichung berechnen

$\(\begin{array}[t]{rlll} \dfrac{f(x)-0}{x-0} &=& f$

Ist $x$ eine Lösung der Gleichung, dann verläuft die Tangente an den Graphen von $f$ im Punkt $(x \mid f(x))$ durch den Koordinatenursprung.

1.5.2 Analytische Geometrie

$\begin{array}[t]{rlll} \pmatrix{4\\3\\0}\circ\pmatrix{-3\\4\\1}&=&-12+12 \\[5pt] &=&0 \end{array}$

$\begin{array}[t]{rlll} \pmatrix{4\\3\\0}\circ\pmatrix{3\\-4\\0}&=&12-12 \\[5pt] &=&0 \end{array}$

Da der Vektor senkrecht zu beiden Spannvektoren der Ebene liegt, steht er somit auch senkrecht zur Ebene $E.$

Für die Länge des Vektors aus Teilaufgabe a) gilt:

$\begin{array}[t]{rlll} \left\vert\pmatrix{4\\3\\0}\right\vert&=&\sqrt{4^2+3^2+0^2} \\[5pt] &=&\sqrt{25} \\[5pt] &=&5 \end{array}$

Ein Punkt auf der Ebene, z.B. der Stützpunkt, der zweimal um diesen Vektor bewegt wird, liegt somit $10\;\text{LE}$ von der Ebene entfernt und der Abstand zu dem gespiegelten Punkt beträgt damit $20\;\text{LE}.$ Es folgt:

$\begin{array}[t]{rlll} \overrightarrow{OP}&=&\pmatrix{1\\-3\\0}+2\cdot\pmatrix{4\\3\\0} \\[5pt] &=&\pmatrix{9\\3\\0} \end{array}$

Mögliche Koordinaten für $P$ sind somit durch $P(9\mid3\mid0)$ gegeben.

1.5.3 Stochastik

Da die Wahrscheinlichkeiten bei $k=10$ und $k=11$ gleich groß und am größten sind, liegt der Erwartungswert $E(X)=n \cdot 0,5$ genau dazwischen - also zwischen zwei ganzen Zahlen. Das geht nur, wenn $n$ ungerade ist.

Gegeben ist $P(X \geq 9) \approx 0,81$ und $P(X=12) \approx 0,14.$ Wegen der Symmetrie gilt dann auch $P(X=9) \approx 0,14.$
Außerdem ist $P(X \geq 11)=0,5,$ also folgt:

$P(X=10) \approx 0,81-0,14-0,5=0,17$

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?