Analytische Geometrie 3 – Pyramide

Die Abbildung zeigt die Pyramide $ABCDS.$ Ihre Grundfläche $ABCD$ ist ein Drachenviereck mit den Eckpunkten $A(0\mid 0\mid 0),$ $B(2\mid 2\mid 0),$ $C(0\mid 6\mid 0)$ und $D(-2\mid 2\mid 0).$ Die Spitze der Pyramide liegt im Punkt $S(0\mid 0\mid 6).$

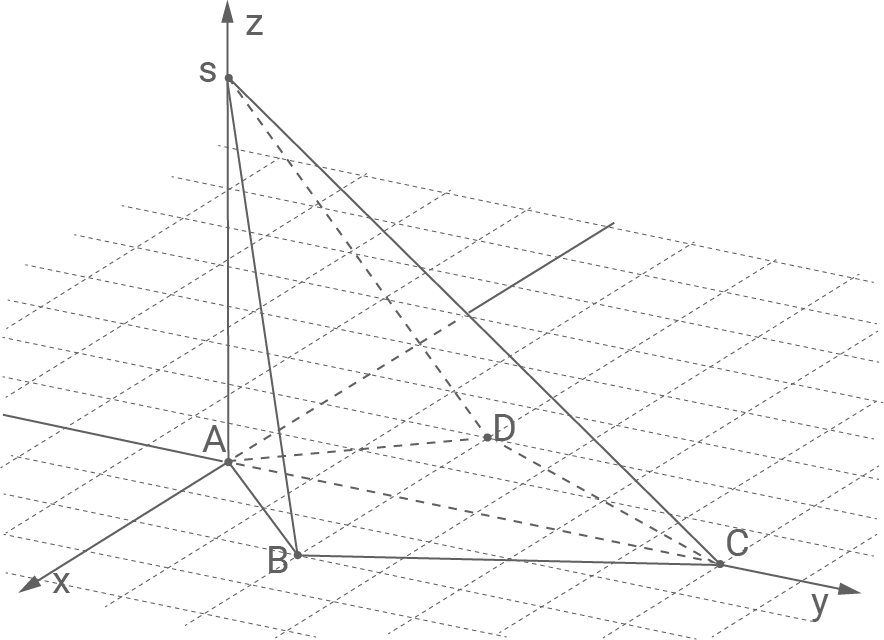
Berechne die Länge der kürzesten und die Länge der längsten der acht Kanten sowie das Volumen der Pyramide $ABCDS.$

(5 BE)

Es gilt: $\left| \overline{\mathrm{DS}} \right|=2 \sqrt{11}.$

Der Punkt $P(-1\mid 1\mid 3)$ liegt auf der Kante $\overline{D S}.$

Begründe ohne Rechnung, dass der Abstand der Punkte $P$ und $D$ $\sqrt{11}$ beträgt.

(2 BE)

Die Seitenfläche $BCS$ der Pyramide liegt in der Ebene $E.$

Ermittle eine Gleichung von $E$ in Koordinatenform.

(zur Kontrolle: $2x+y+z=6$ )

(3 BE)

Bestimme die Größe des Winkels, den die Ebene $E$ mit der $xy$ -Ebene einschließt.

(2 BE)

Der Punkt $B$ wird nun so parallel zur $y$ -Achse verschoben, dass für den dadurch entstehenden Punkt $\(B$ gilt:

Das Viereck $\(AB$ hat in $\(B$ einen rechten Innenwinkel.

Um die Koordinaten von $\(B$ zu bestimmen, kann folgender Ansatz verwendet werden:

$\pmatrix{2\\y\\0}\circ \pmatrix{2\\y-6\\0}=0$

Erläutere diesen Ansatz.

(3 BE)

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?

Längste Kantenlänge: $\left| \overline{CS} \right|= \left| \pmatrix{0\\-6\\6} \right|=6\sqrt{2}$

Kleinste Kantenlänge: $\left| \overline{AB} \right|= \left| \pmatrix{2\\2\\0} \right|=2\sqrt{2}$

Das Koordinatengitter in der Abbildung zeigt, dass die Grundfläche ein Drachenviereck mit Diagonalen der Länge $4\;\text{LE}$ und $6\;\text{LE}$ ist. Der Flächeninhalt $A$ der Grundfläche ist somit gegeben durch:

$\begin{array}[t]{rlll} A&=&\dfrac{1}{2}\cdot4\cdot6 \\[5pt] &=&12\;[\text{FE}] \end{array}$

Da die Grundfläche der Pyramide in der $x_1x_2$ -Ebene liegt, folgt aus den Koordinaten von $S,$ dass die Pyramide eine Höhe von $6\;\text{LE}$ besitzt. Damit ergibt sich für das Volumen $V$ der Pyramide:

$\begin{array}[t]{rlll} V&=&\dfrac{1}{3}\cdot12\cdot6 \\[5pt] &=&24\;[\text{VE}] \end{array}$

Da $P(-1|1| 3)$ der Mittelpunkt von $\overline{D S}$ ist, liegt er genau in der Mitte der Strecke. Die Gesamtlänge von $\overline{D S}$ beträgt $2 \sqrt{11}$ , daher ist der Abstand von $P$ zu $D$ bzw. $S$ die Hälfte davon:

$\overline{PD}=\overline{PS}=\sqrt{11}$

Zwei mögliche Spannvektoren der Ebene $E$ sind gegeben durch:

$\begin{array}[t]{rlll} \overrightarrow{BC}&=&\pmatrix{0\\6\\0}-\pmatrix{2\\2\\0} \\[5pt] &=&\pmatrix{-2\\4\\0} \end{array}$

$\begin{array}[t]{rlll} \overrightarrow{BS}&=&\pmatrix{0\\0\\6}-\pmatrix{2\\2\\0} \\[5pt] &=&\pmatrix{-2\\-2\\6} \end{array}$

Ein Normalenvektor der Ebene $E$ muss somit die folgenden beiden Bedingungen erfüllen:

$\pmatrix{n_1\\n_2\\n_3}\circ\pmatrix{-2\\4\\0}=0;\pmatrix{n_1\\n_2\\n_3}\circ\pmatrix{-2\\4\\0}=0$

Daraus ergibt sich das folgende Gleichungssystem:

$\begin{array}{lrll} \text{I}\quad&-2n_1+4n_2&=& 0 & \\ \text{II}\quad&-2n_1-2n_2+6n_3&=& 0 & \\ \end{array}$

Da der Normalenvektor beliebig skaliert werden kann, kann einer der drei Einträge frei gewählt werden. Mit $n_1=2$ liefert Gleichung $\text{I}$ somit z.B. direkt $n_2=1.$ Einsetzen dieser beiden Werte in Gleichung $\text{II}$ ergibt:

$\begin{array}[t]{rlll} -2\cdot2-2\cdot1+6n_3&=&0 &\mid\;+6 \\[5pt] 6n_3&=&6 &\mid\;:6 \\[5pt] n_3&=&1 \end{array}$

Ein möglicher Normalenvektor der Ebene $E$ ist somit durch $\pmatrix{2\\1\\1}$ gegeben und $E$ hat damit eine Gleichung der Form $2x+y+z=d.$ Einsetzen der Koordinaten von $S$ in diese Gleichung liefert direkt $d=6,$ sodass insgesamt folgt:

$E:2x+y+z=6$

$\begin{array}[t]{rlll} \cos(\alpha)&=&\dfrac{\pmatrix{2\\1\\1}\circ \pmatrix{0\\0\\1}}{\left| \pmatrix{2\\1\\1} \right|\cdot \left| \pmatrix{0\\0\\1} \right|} \\[5pt] \cos(\alpha)&=&\dfrac{1}{\sqrt{6}} \\[5pt] \alpha&=&\cos^{-1}\left(\dfrac{1}{\sqrt{6}}\right) \\[5pt] \alpha&\approx&65,9^\circ \end{array}$

Da $B$ nur entlang der $y$ -Achse verschoben wird, können die Koordinaten von $\(B$ in der Form $(2\mid y\mid 0)$ geschrieben werden. Damit folgt:

$\(\begin{array}[t]{rlll} \overrightarrow{CB$

$\(\begin{array}[t]{rlll} \overrightarrow{AB$

Der zwischen diesen Vektoren eingeschlossene Winkel entspricht dem im Punkt $\(B$ Wenn das Skalarprodukt aus der Aufgabenstellung also gleich Null ist, liegt im Punkt $\(B$ ein rechter Winkel vor.

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?