Teil B1
Die Fahrbahn einer Autorennstrecke kann in einem Koordinatensystem (1 Einheit entspricht 100 Meter) dargestellt werden.
lhr Verlauf kann im betrachteten Teilstück durch den Graphen der Funktion mit
mit 
 näherungsweise beschrieben werden. Die Breite der Fahrbahn wird vernachlässigt.
näherungsweise beschrieben werden. Die Breite der Fahrbahn wird vernachlässigt.
Die Punkte und
und  liegen auf dieser Fahrbahn.
liegen auf dieser Fahrbahn.
Im gegebenen Koordinatensystem besitzen diese Punkte die Koordinaten ,
,  ,
,  und
und  .
.
 Abbildung (nicht maßstäblich)
Abbildung (nicht maßstäblich)
Die Firma gibt bezüglich der Produktion dieser Teile an:
lhr Verlauf kann im betrachteten Teilstück durch den Graphen der Funktion
Die Punkte
Im gegebenen Koordinatensystem besitzen diese Punkte die Koordinaten
1.1
Der Graph der Funktion  besitzt genau zwei Wendepunkte.
besitzt genau zwei Wendepunkte.
Zeige, dass die Punkte und
und  diese beiden Wendepunkte sind.
diese beiden Wendepunkte sind.
Zwischen den Punkten und
und  existiert ein geradliniger Verbindungsweg.
Weise nach, dass dieser Weg etwa
existiert ein geradliniger Verbindungsweg.
Weise nach, dass dieser Weg etwa  m lang ist.
m lang ist.
Zeige, dass die Punkte
Zwischen den Punkten
(7P)
1.2
Ein Rennwagen benötigt für die Fahrt auf der Fahrbahn zwischen den Punkten  und
und  eine Zeit von
eine Zeit von  Sekunden.
Berechne die Durchschnittsgeschwindigkeit des Rennwagens zwischen den Punkten
Sekunden.
Berechne die Durchschnittsgeschwindigkeit des Rennwagens zwischen den Punkten  und
und  in
in  .
.
(6P)
1.3
Zum Schutz der Rennfahrer wird eine Auslaufzone gebaut.
In der Auslaufzone soll ein Rennwagen, welcher von der Fahrbahn abkommt, stark abgebremst werden. Die Auslaufzone wird im Koordinatensystem durch den Graphen der Funktion mit
mit 
 und den Graphen der Funktion
und den Graphen der Funktion  vollständig begrenzt.
vollständig begrenzt.
Die Auslaufzone ist mit einer cm dicken Kiesschicht belegt.
cm dicken Kiesschicht belegt.
Bestimme das Volumen dieser Kiesschicht.
In der Auslaufzone soll ein Rennwagen, welcher von der Fahrbahn abkommt, stark abgebremst werden. Die Auslaufzone wird im Koordinatensystem durch den Graphen der Funktion
Die Auslaufzone ist mit einer
Bestimme das Volumen dieser Kiesschicht.
(7P)
Eine geradlinig verlaufende Leitplanke soll zusätzlichen Schutz bieten.
Wenn ein Rennwagen von in Richtung
in Richtung  fährt und im Punkt
fährt und im Punkt  tangential die Fahrbahn verlässt, dann trifft er bei geradliniger Fahrt nach etwa
tangential die Fahrbahn verlässt, dann trifft er bei geradliniger Fahrt nach etwa  m im Punkt
m im Punkt  auf die Leitplanke (siehe Abbildung).
auf die Leitplanke (siehe Abbildung).
Ein Endpunkt der Leitplanke ist .
.
Die Dicke der Leitplanke wird vernachlässigt.
Wenn ein Rennwagen von
Ein Endpunkt der Leitplanke ist
Die Dicke der Leitplanke wird vernachlässigt.
 Abbildung (nicht maßstäblich)
Abbildung (nicht maßstäblich)
1.4
Zeige, dass der Punkt  näherungsweise die Koordinaten
näherungsweise die Koordinaten  besitzt.
besitzt.
Der Punkt ist der Mittelpunkt der Leitplanke.
ist der Mittelpunkt der Leitplanke.
Bestimme die Koordinaten des Endpunktes der Leitplanke.
der Leitplanke.
Ermittle die minimale Entfernung der Fahrbahn der Autorennstrecke vom Mittelpunkt der Leitplanke.
Der Punkt
Bestimme die Koordinaten des Endpunktes
Ermittle die minimale Entfernung der Fahrbahn der Autorennstrecke vom Mittelpunkt der Leitplanke.
(13P)
1.5
Es gibt einen Bereich der Fahrbahn der Autorennstrecke, für den gilt:
Wenn ein Rennwagen in diesem Bereich bei der Fahrt von nach
nach  tangential von der Fahrbahn abkommt und geradlinig weiterfährt, dann trifft er auf die Leitplanke
tangential von der Fahrbahn abkommt und geradlinig weiterfährt, dann trifft er auf die Leitplanke  .
.
Bestimme die Koordinaten des Punktes der Fahrbahn, in dem dieser Bereich von
der Fahrbahn, in dem dieser Bereich von  ausgehend beginnt.
ausgehend beginnt.
Eine Firma stellt Teile für die Leitplanke her. Jedes Teil wird zunächst zu einem Profil gebogen und danach beschichtet.
Wenn ein Rennwagen in diesem Bereich bei der Fahrt von
Bestimme die Koordinaten des Punktes
(5P)
Die Firma gibt bezüglich der Produktion dieser Teile an:
aller Teile sind fehlerhaft im Profil.
aller Teile sind fehlerhaft in der Beschichtung.
aller Teile sind fehlerfrei, d. h., sie besitzen keinen Fehler im Profil und keinen Fehler in der Beschichtung.
1.6
Der Produktion der Firma werden  Teile zufällig entnommen.
Teile zufällig entnommen.
Berechne die Wahrscheinlichkeit dafür, dass darunter mehr fehlerfreie Teile sind, als zu erwarten ist.
Berechne die Wahrscheinlichkeit dafür, dass darunter mehr fehlerfreie Teile sind, als zu erwarten ist.
(6P)
1.7
Ein der Produktion der Firma zufällig entnommenes Teil besitzt keinen Fehler in der Beschichtung.
Bestimme die Wahrscheinlichkeit dafür, dass dieses Teil fehlerhaft im Profil ist.
Bestimme die Wahrscheinlichkeit dafür, dass dieses Teil fehlerhaft im Profil ist.
(6P)
1.1
2nd  calc
calc  Max/Min
Max/Min
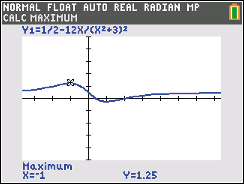 Abb. 1: Maximum der Ableitungsfunktion
Abb. 1: Maximum der Ableitungsfunktion
1.2
2nd  calc
calc 
Rechne also
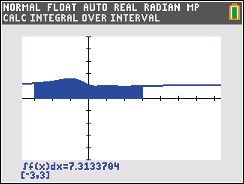 Abb. Zahl: Bogenlänge
Abb. Zahl: Bogenlänge
1.3
2nd  calc
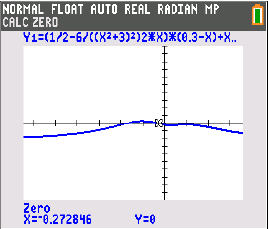
calc  zero
zero
Berechne also nun den Wert des Integrals
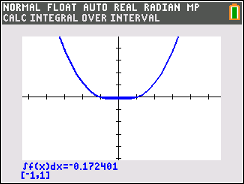 Abb. 3: Der Flächeninhalt der Differenzfunktion
Abb. 3: Der Flächeninhalt der Differenzfunktion
1.4
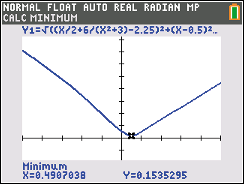 Abb. 4: Das Minimum der Abstandsfunktion
Abb. 4: Das Minimum der Abstandsfunktion
1.5
1.6
2nd  distr
distr  binomcdf
binomcdf
Damit berechnest du nun die Wahrscheinlichkeit, dass die Trefferanzhal kleiner oder gleich 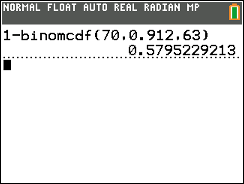 Abb. 6: Die Wahrscheinlichkeit für mehr fehlerfreie Teile, als zu erwarten wären
Abb. 6: Die Wahrscheinlichkeit für mehr fehlerfreie Teile, als zu erwarten wären
1.7
© 2016 - SchulLV.
1.1
2nd  calc
calc  Max/Min
Max/Min
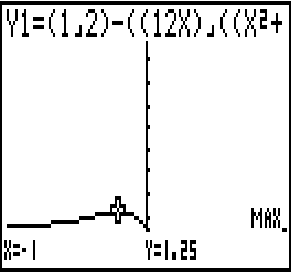 Abb. 1: Maximum der Ableitungsfunktion
Abb. 1: Maximum der Ableitungsfunktion
1.2
2nd  calc
calc 
Rechne also
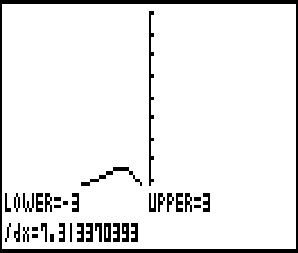 Abb. Zahl: Bogenlänge
Abb. Zahl: Bogenlänge
1.3
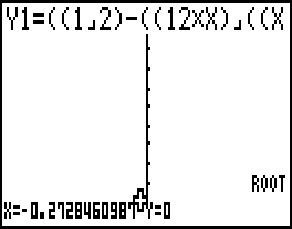
SHIFT  GSOLVE
GSOLVE  ROOT
ROOT
Berechne also nun den Wert des Integrals
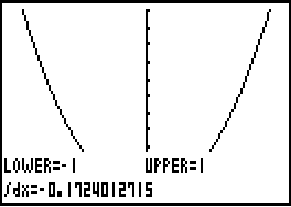 Abb. 3: Der Flächeninhalt der Differenzfunktion
Abb. 3: Der Flächeninhalt der Differenzfunktion
1.4
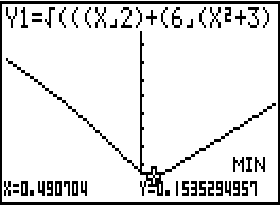 Abb. 4: Das Minimum der Abstandsfunktion
Abb. 4: Das Minimum der Abstandsfunktion
1.5
1.6
DIST  BINOM
BINOM  BCD
BCD
Damit berechnest du nun die Wahrscheinlichkeit, dass die Trefferanzhal kleiner oder gleich 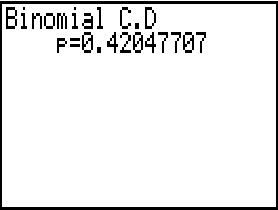 Abb. 6: Die Gegenwahrscheinlichkeit für mehr fehlerfreie Teile, als zu erwarten wären
Abb. 6: Die Gegenwahrscheinlichkeit für mehr fehlerfreie Teile, als zu erwarten wären
1.7
© 2016 - SchulLV.