Teil A
1.
In den Aufgaben 1.1 bis 1.5 ist von den jeweils fünf Auswahlmöglichkeiten genau eine Antwort richtig. Kreuze das jeweilige Feld an.
1.1
Welche der folgenden auf  definierten Funktionen besitzt genau drei Nullstellen?
definierten Funktionen besitzt genau drei Nullstellen?
1.2
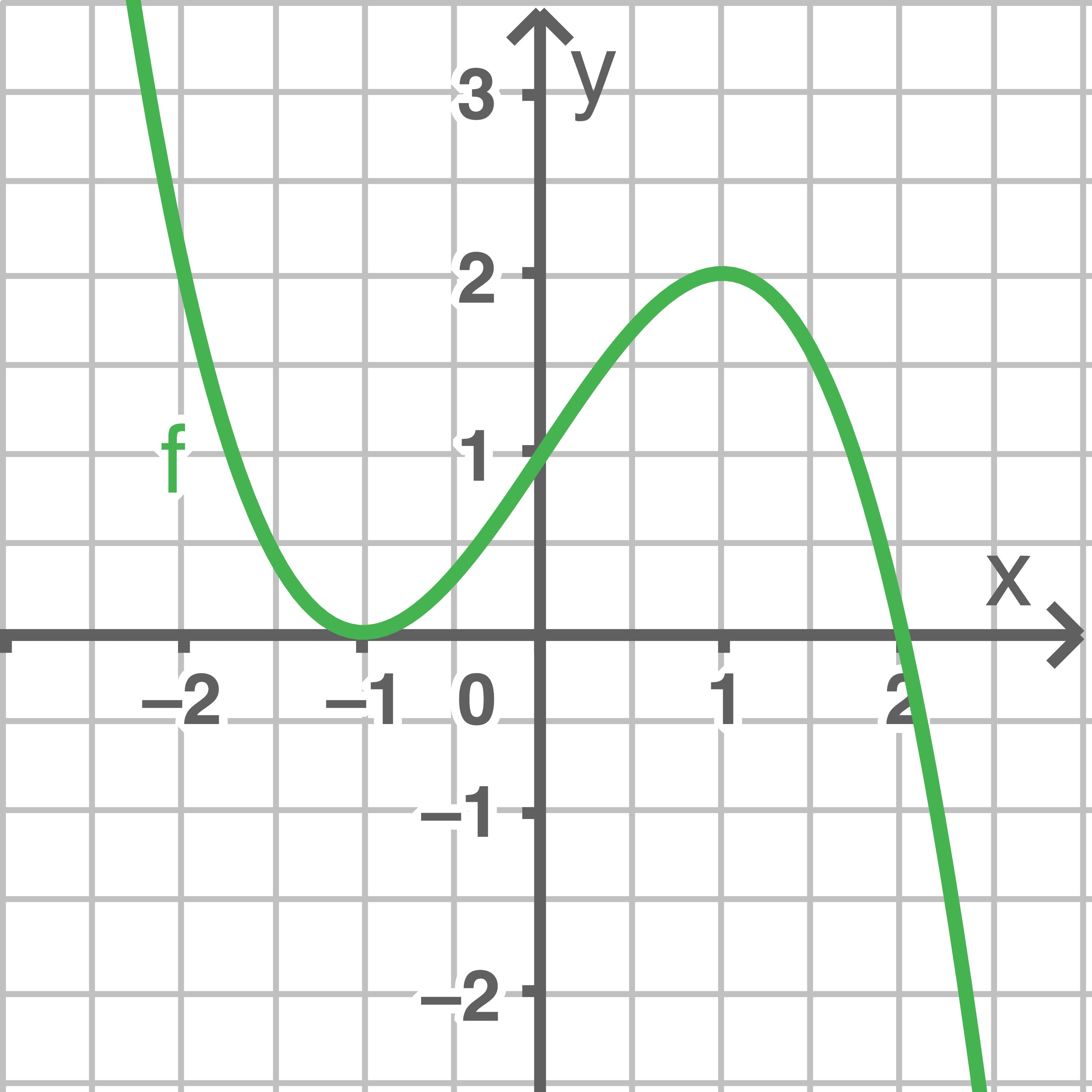
Die Abbildung zeigt den Graphen einer ganzrationalen Funktion  Welche Aussage trifft im dargestellten Intervall zu?
Welche Aussage trifft im dargestellten Intervall zu?
1.3
Für welchen reellen Wert von  sind die Vektoren
sind die Vektoren  und
und  orthogonal zueinander?
orthogonal zueinander?
1.4
Die Abbildung zeigt für einen positiven reellen Wert  einen Ausschnitt der Ebene
einen Ausschnitt der Ebene  in einem kartesischen Koordinatensystem mit dem Koordinantenursprung
in einem kartesischen Koordinatensystem mit dem Koordinantenursprung  Die Ebene
Die Ebene  kann durch folgende Gleichung beschrieben werden:
kann durch folgende Gleichung beschrieben werden:
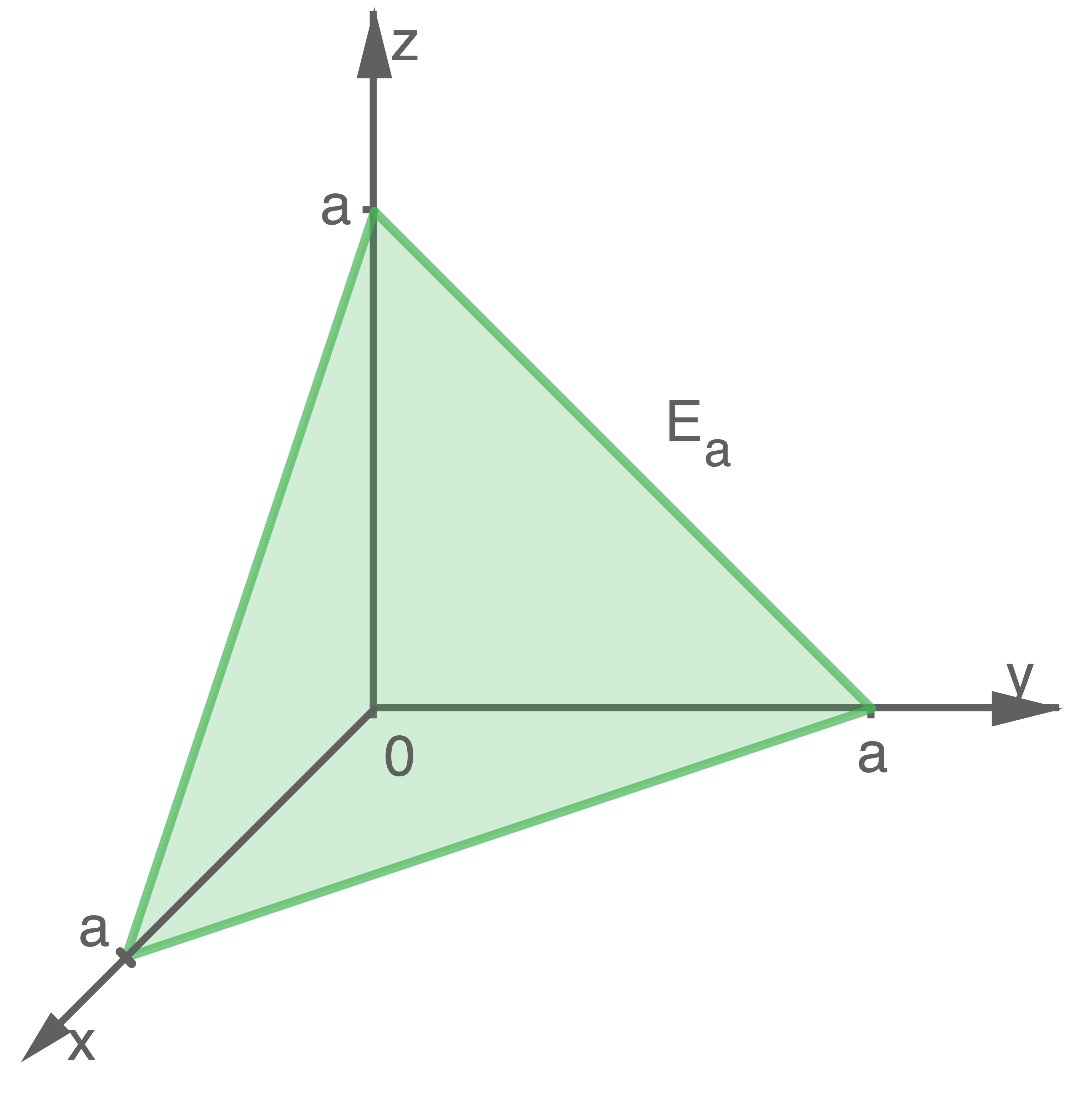
Abbildung (nicht maßstäblich)
1.5
Beim Wurf einer verbeulten Münze fällt das Wappen mit der Wahrscheinlichkeit  . Die Wahrscheinlichkeit dafür, dass beim 10-maligen Werfen dieser Münze genau zweimal Wappen fällt, lässt sich mit folgendem Term berechnen:
. Die Wahrscheinlichkeit dafür, dass beim 10-maligen Werfen dieser Münze genau zweimal Wappen fällt, lässt sich mit folgendem Term berechnen:
Für Aufgabe 1 erreichbare BE-Anzahl: 10
2
Der abgebildete Graph  stellt eine Funktion
stellt eine Funktion  dar.
dar.
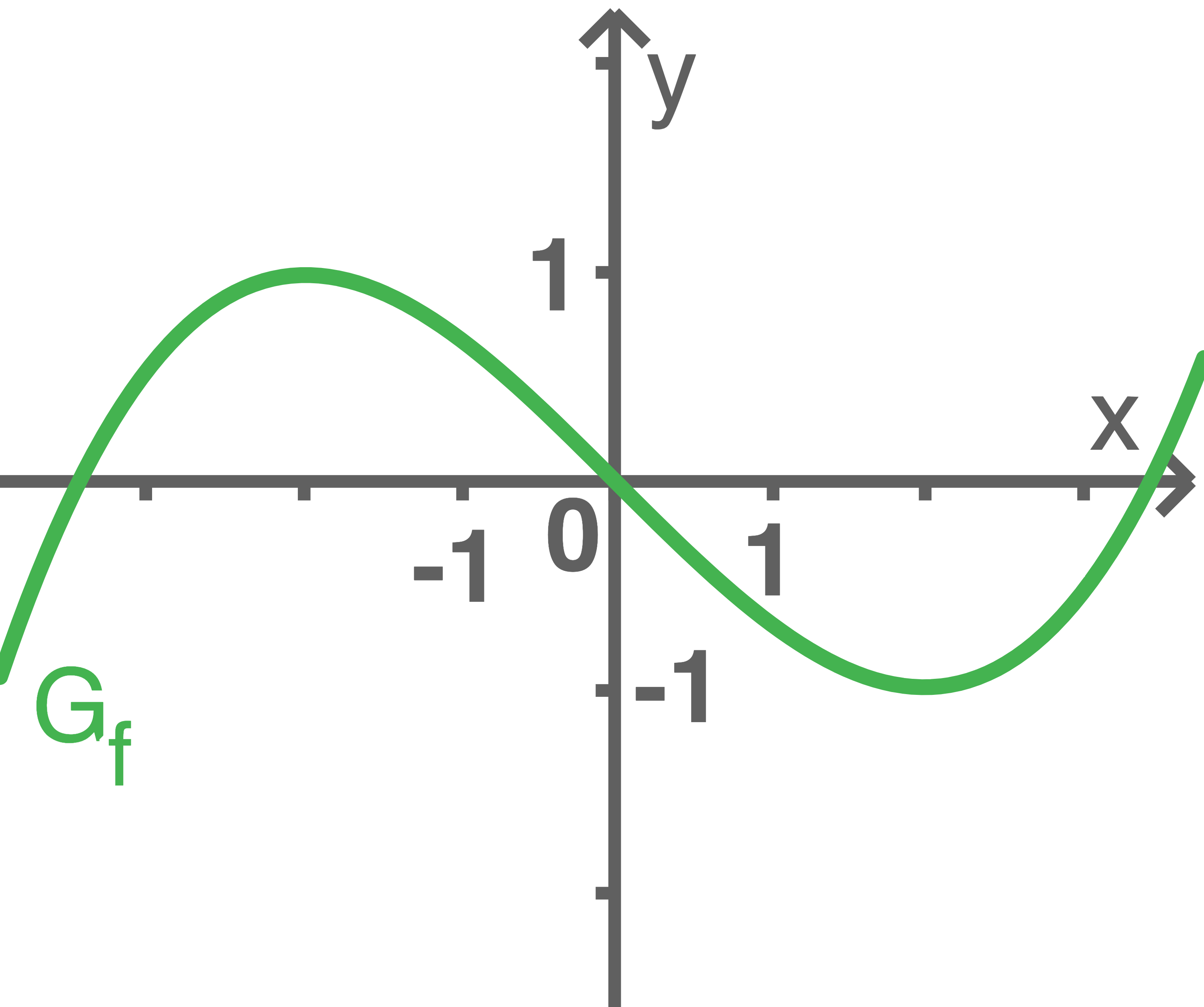

2.1
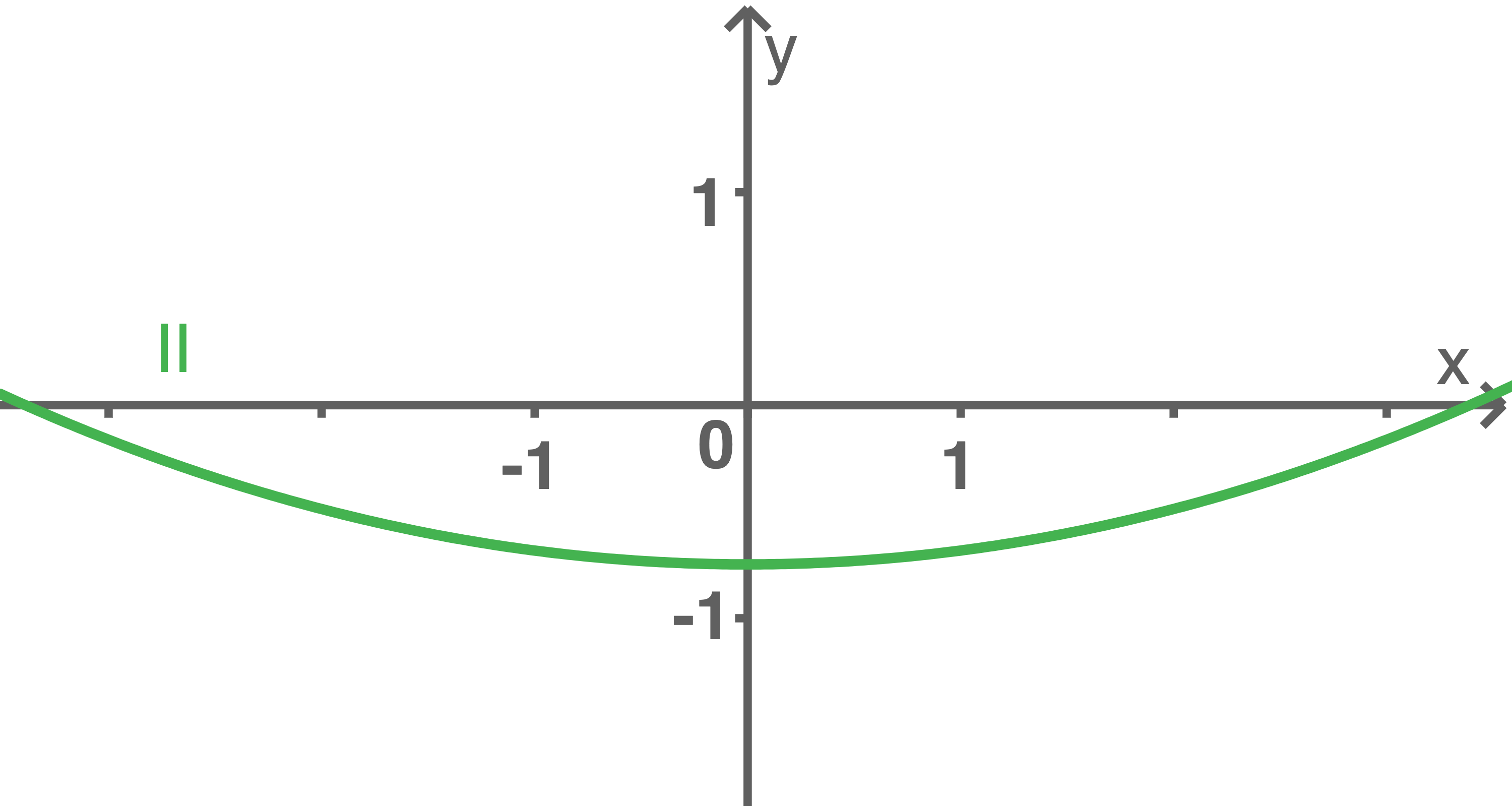
Einer der folgenden Graphen 
 oder
oder  gehört zur ersten Ableitungsfunktion von
gehört zur ersten Ableitungsfunktion von  Gib diesen Graphen an. Begründe, dass die beiden anderen Graphen dafür nicht infrage kommen.
Gib diesen Graphen an. Begründe, dass die beiden anderen Graphen dafür nicht infrage kommen.
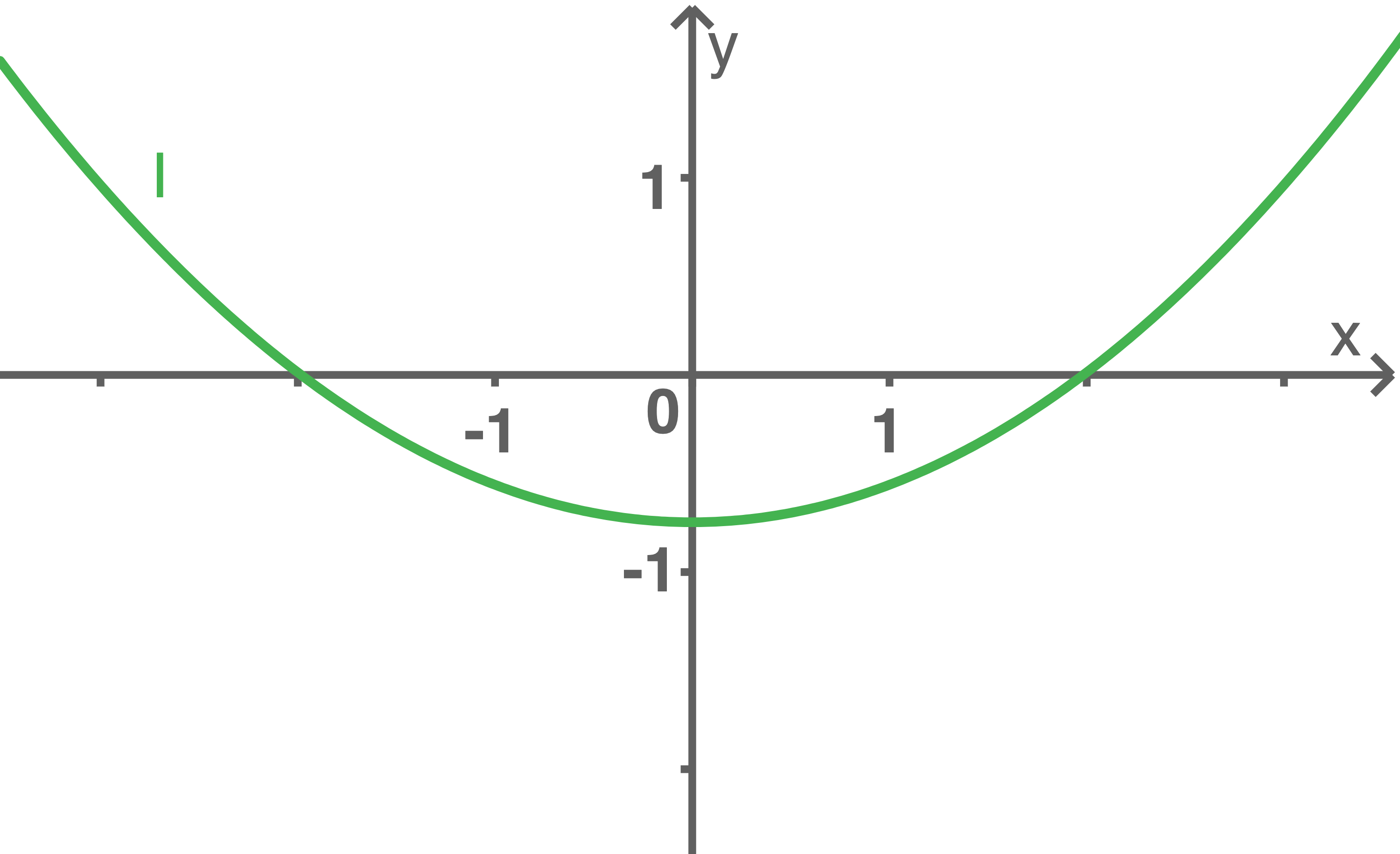



Erreichbare BE-Anzahl: 03
2.2
Die Funktion  ist eine Stammfunktion von
ist eine Stammfunktion von  Gib das Monotonieverhalten von
Gib das Monotonieverhalten von  im Intervall
im Intervall ![\([1;3]\)](https://www.schullv.de/resources/formulas/4c871f3c45250ceb60647b58544ce3c3596fbc24341f187d6b6947c96521272c_light.svg) an. Begründe deine Angabe.
an. Begründe deine Angabe.
Erreichbare BE-Anzahl: 02
3.
In einem kartesischen Koordinatensystem sind die Ebenen  mit
mit
 und
und  mit
mit  gegeben.
gegeben.
3.1
Gib die Koordinaten eines Punktes an, der in  liegt.
liegt.
Erreichbare BE-Anzahl: 01
3.2
Zeige, dass  parallel zu
parallel zu  ist.
ist.
Erreichbare BE-Anzahl: 02
3.3
Gib eine Gleichung einer Ebene an, die senkrecht zu  ist und den Koordinatenursprung enthält.
ist und den Koordinatenursprung enthält.
Erreichbare BE-Anzahl: 02
4
Ein Glücksrad besteht aus fünf gleich großen Sektoren. Einer der Sektoren ist mit „0“ beschriftet, einer mit „1“ und einer mit „2“, die beiden anderen Sektoren sind mit „9“ beschriftet.
4.1
Das Glücksrad wird viermal gedreht. Berechne die Wahrscheinlichkeit dafür, dass die Zahlen 

 und
und  in der angegebenen Reihenfolge erzielt werden.
in der angegebenen Reihenfolge erzielt werden.
Erreichbare BE-Anzahl: 02
4.2
Das Glücksrad wird zweimal gedreht. Bestimme die Wahrscheinlichkeit dafür, dass die Summe der erzielten Zahlen mindestens  beträgt.
beträgt.
Erreichbare BE-Anzahl: 03
5
Im Folgenden wird die gegenseitige Lage von Ebenen und Punkten mit drei gleichen Koordinaten betrachtet.
5.1
Die Ebene  enthält einen Punkt, dessen drei Koordinaten übereinstimmen. Bestimme diese Koordinaten.
enthält einen Punkt, dessen drei Koordinaten übereinstimmen. Bestimme diese Koordinaten.
Erreichbare BE-Anzahl: 02
5.2
Begründe, dass die folgende Aussage richtig ist:
Es gibt unendlich viele Ebenen, die keinen Punkt enthalten, dessen drei Koordinaten übereinstimmen.
Erreichbare BE-Anzahl: 03
1.1
1.2
1.3
1.4
1.5
2.1
Graph  schneidet die
schneidet die  -Achse an den Stellen
-Achse an den Stellen  und
und  An diesen Stellen müsste der Graph von
An diesen Stellen müsste der Graph von  also die Steigung
also die Steigung  haben. Dies ist aber nicht der Fall. Graph
haben. Dies ist aber nicht der Fall. Graph  kann also nicht zur Ableitungsfunktion
kann also nicht zur Ableitungsfunktion  von
von  gehören.
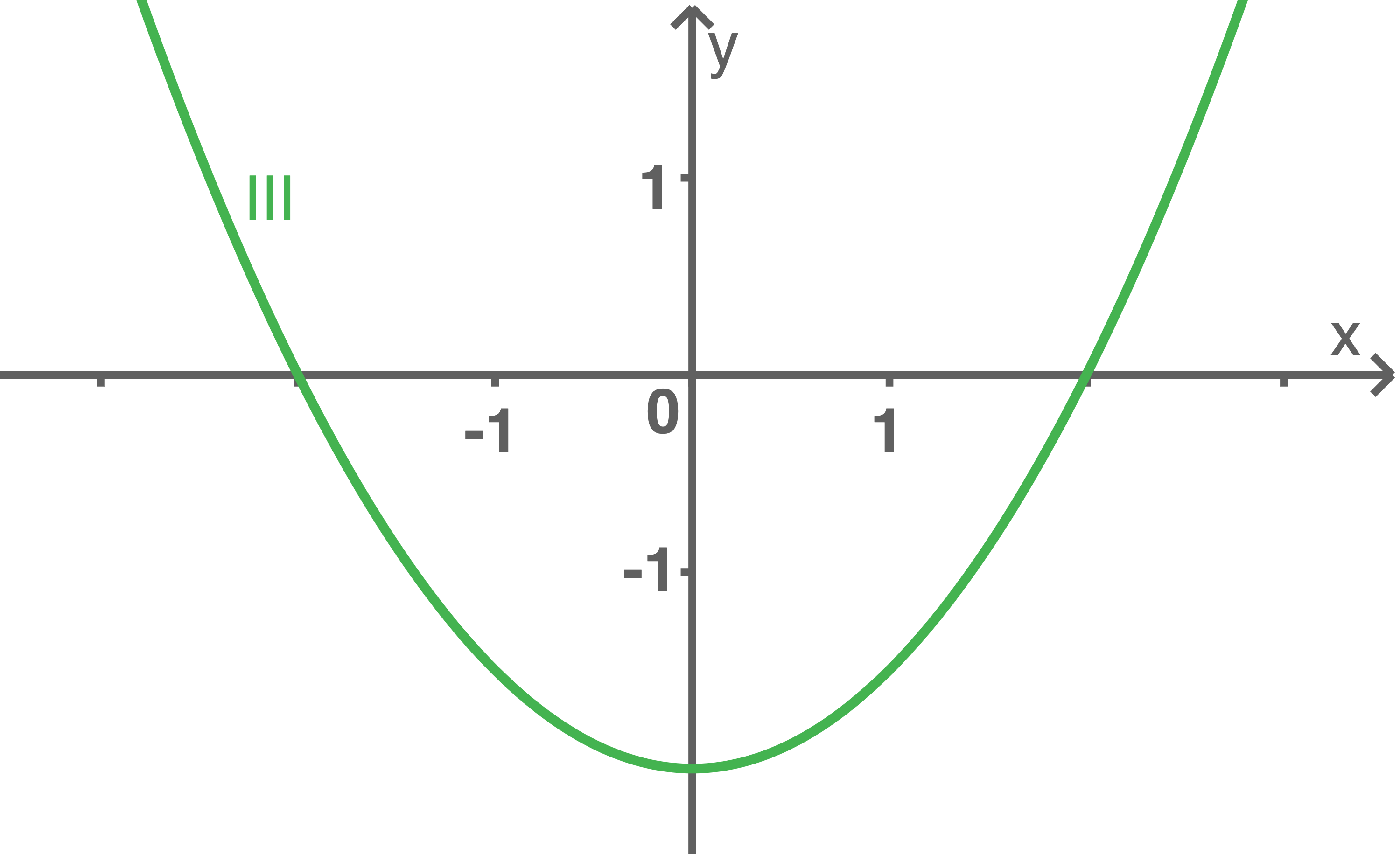
Graph
gehören.
Graph  schneidet die
schneidet die  -Achse im Punkt
-Achse im Punkt  Der Graph von
Der Graph von  müsste daher an der Stelle
müsste daher an der Stelle  die Steigung
die Steigung  besitzen. Eine Tangente an
besitzen. Eine Tangente an  bei
bei  widerlegt diese Steigung. Graph
widerlegt diese Steigung. Graph  kann also nicht zur Ableitungsfunktion
kann also nicht zur Ableitungsfunktion  von
von  gehören.
Damit gehört Graph
gehören.
Damit gehört Graph  zur ersten Ableitungsfunktion von
zur ersten Ableitungsfunktion von 
2.2
Im Intervall ![\([1;3]\)](https://www.schullv.de/resources/formulas/4c871f3c45250ceb60647b58544ce3c3596fbc24341f187d6b6947c96521272c_light.svg) liegt der Graph von
liegt der Graph von  ausschließlich unterhalb der
ausschließlich unterhalb der  -Achse. Damit ist die zugehörige Stammfunktion in diesem Intervall streng monoton fallend.
-Achse. Damit ist die zugehörige Stammfunktion in diesem Intervall streng monoton fallend.
3.1
Durch beliebiges Wählen von  und
und  lässt sich
lässt sich  berechnen. Beispiel:
Für
berechnen. Beispiel:
Für  folgt:
folgt:
![\(\begin{array}[t]{rll}
-x + 2y + z& =& 1 \\[5pt]
0 + 0 +z &=& 1 &\\[5pt]
z &=& 1 \\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/b2766bd612c0c39f41898e2040996cae50ea3bb15c7294ae09d4452414bc00c3_light.svg) Ein Punkt, der in
Ein Punkt, der in  liegt, lautet also beispielsweise
liegt, lautet also beispielsweise 
3.2
Dies ist der Fall, wenn das jeweils zugehörige Skalarprodukt Null ist: Die beiden Ebenen
3.3
Da die Spannevktoren von  orthogonal zum Normalenvektor von
orthogonal zum Normalenvektor von  sind, können sie als Normalenvektor der neuen Ebene dienen. Damit folgt:
sind, können sie als Normalenvektor der neuen Ebene dienen. Damit folgt:
 Einsetzen der Koordinaten des Koordinatenursprungs
Einsetzen der Koordinaten des Koordinatenursprungs  liefert:
liefert:
![\(\begin{array}[t]{rll}
x+y-z &=& d \\[5pt]
0+0-0 &=& d \\[5pt]
0 &=& d
\end{array}\)](https://www.schullv.de/resources/formulas/6e7c18c6c7e6318822b38a722d36b59c9dd7f9a8ed8af819b71848b6cc51a7f1_light.svg) Eine Gleichung einer Ebene
Eine Gleichung einer Ebene  die senkrecht zu
die senkrecht zu  ist und den Koordinatenursprung enthält, lautet:
ist und den Koordinatenursprung enthält, lautet:
 Es gibt unendlich viele weitere mögliche Ebenen
Es gibt unendlich viele weitere mögliche Ebenen  .
.
4.1
Es gilt  und
und  Mit der Pfadmultiplikationsregel folgt:
Mit der Pfadmultiplikationsregel folgt:
 Mit einer Wahrscheinlichkeit von
Mit einer Wahrscheinlichkeit von  werden die Zahlen
werden die Zahlen 

 und
und  genau in der angegebenen Reihenfolge erzielt.
genau in der angegebenen Reihenfolge erzielt.
4.2
Mögliche Kombinationen: 
 Mit einer Wahrscheinlichkeit von
Mit einer Wahrscheinlichkeit von  beträgt die Summe der beiden erzielten Zahlen mindestens
beträgt die Summe der beiden erzielten Zahlen mindestens 
5.1
Der gesuchte Punkt besitzt Koordinaten der Form  Durch Einsetzen in die Ebenengleichung folgt:
Durch Einsetzen in die Ebenengleichung folgt:
![\(\begin{array}[t]{rll}
3x +2y +2z &=& 6 \\[5pt]
3t+2t+2t &=& 6 \\[5pt]
7t &=& 6 &\quad \scriptsize \mid\; :7 \\[5pt]
t &=& \dfrac{6}{7}
\end{array}\)](https://www.schullv.de/resources/formulas/e5e7016e869dc296cf4d93c0874f03e15266ce2fff052faba7bdf33f8d8c4a75_light.svg) Die Koordinaten des gesuchten Punkts der Ebene
Die Koordinaten des gesuchten Punkts der Ebene  mit drei übereinstimmenden Koordinaten lauten
mit drei übereinstimmenden Koordinaten lauten 
5.2
Alle Punkte, deren drei Koordinaten übereinstimmen, liegen auf der Geraden  mit der Gleichung
mit der Gleichung  Alle Ebenen, die zu dieser Geraden parallel verlaufen, diese aber nicht enthalten, haben keine gemeinsamen Punkte mit ihr und daher keinen Punkt, dessen drei Koordinaten übereinstimmen. Zu jeder Geraden gibt es unendlich viele Ebenen, die zu dieser parallel verlaufen und diese nicht enthalten. Auch zu
Alle Ebenen, die zu dieser Geraden parallel verlaufen, diese aber nicht enthalten, haben keine gemeinsamen Punkte mit ihr und daher keinen Punkt, dessen drei Koordinaten übereinstimmen. Zu jeder Geraden gibt es unendlich viele Ebenen, die zu dieser parallel verlaufen und diese nicht enthalten. Auch zu  gibt es daher unendlich viele parallele Ebenen, die
gibt es daher unendlich viele parallele Ebenen, die  nicht enthalten, die also keinen Punkt mit drei identischen Koordinaten besitzen.
nicht enthalten, die also keinen Punkt mit drei identischen Koordinaten besitzen.