Teil B1
Eine Landschaft besteht aus Festland I, Festland II und einem Meer. In die Landschaft ist ein kartesisches Koordinatensystem (1 Längeneinheit entspricht 1 Kilometer) gelegt. Der Verlauf der Küstenlinie von Festland I wird für  durch den Graphen der Funktion
durch den Graphen der Funktion  mit
mit

 beschrieben (siehe Abbildung). Der Parameter
beschrieben (siehe Abbildung). Der Parameter  beschreibt die Veränderungen der Küstenlinie von Festland I im Laufe der Zeit. Zum gegenwärtigen Zeitpunkt gilt
beschreibt die Veränderungen der Küstenlinie von Festland I im Laufe der Zeit. Zum gegenwärtigen Zeitpunkt gilt  Die Punkte
Die Punkte 
 und
und  liegen auf dem Graphen der Funktion
liegen auf dem Graphen der Funktion  Der Punkt
Der Punkt  ist lokaler Minimumpunkt des Graphen von
ist lokaler Minimumpunkt des Graphen von 
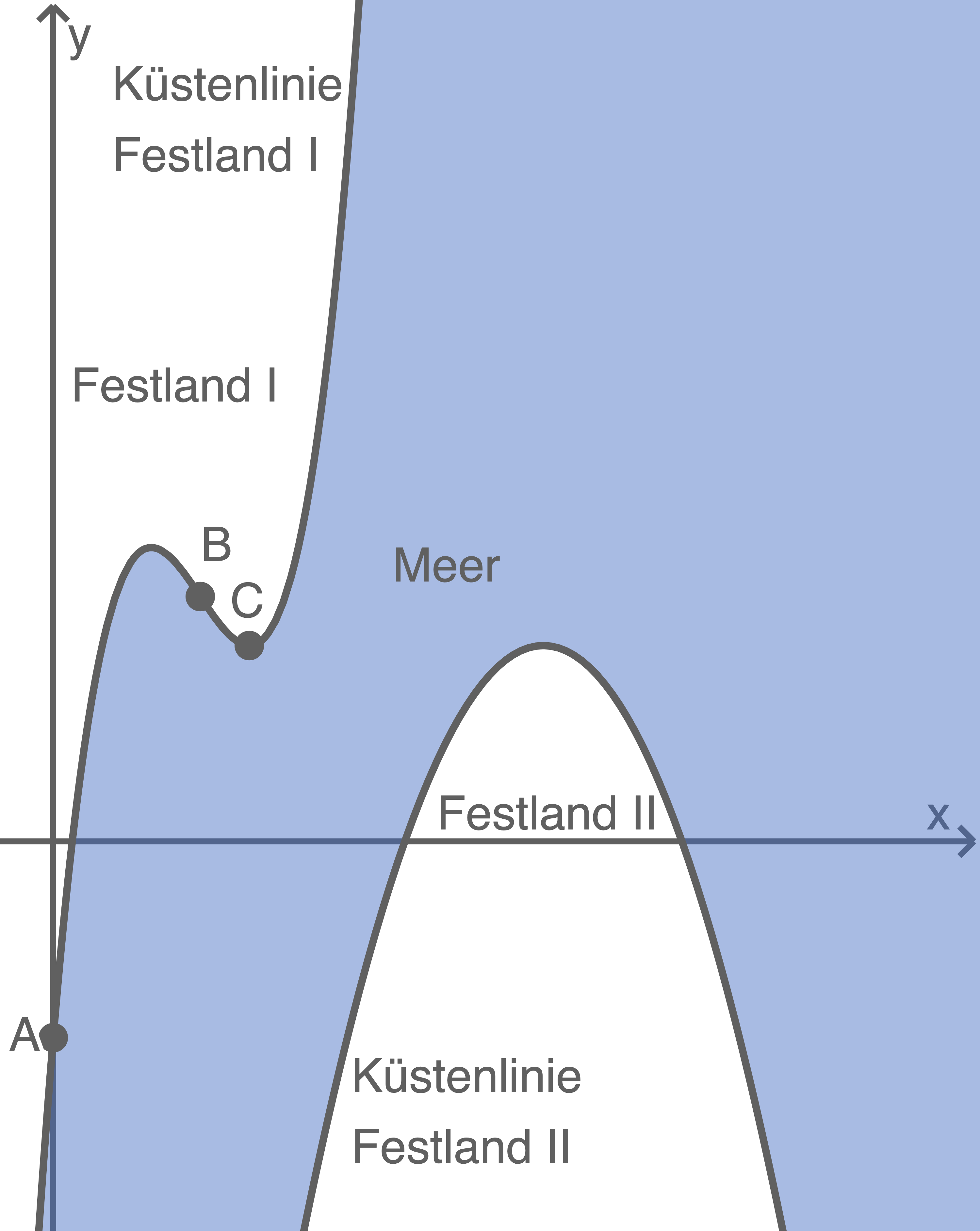
Abbildung (nicht maßstäblich)
1.1
Gib die Koordinaten des lokalen Maximumpunktes des Graphen von  an.
an.
Zeige, dass der Graph der Funktion im Punkt
im Punkt  einen Wendepunkt besitzt.
einen Wendepunkt besitzt.
Zeige, dass der Graph der Funktion
Erreichbare BE-Anzahl: 04
1.2
Der Punkt  liegt auf der Ordinatenachse. Eine Gerade verläuft durch die Punkte
liegt auf der Ordinatenachse. Eine Gerade verläuft durch die Punkte  und
und  . Bestimme den Schnittwinkel zwischen dieser Geraden und der Ordinatenachse.
. Bestimme den Schnittwinkel zwischen dieser Geraden und der Ordinatenachse.
Erreichbare BE-Anzahl: 04
1.3
Ein Strandwanderweg verläuft entlang der Küstenlinie von Festland I von  über
über  zu einem Zielpunkt
zu einem Zielpunkt  .
.
Ermittle die Läge des Strandwanderweges von bis
bis 
Der Strandwanderweg von über
über  bis zu
bis zu  besitzt eine Länge von
besitzt eine Länge von 
Ermittle die Koordinaten von
Ermittle die Läge des Strandwanderweges von
Der Strandwanderweg von
Ermittle die Koordinaten von
Erreichbare BE-Anzahl: 06
1.4
Zum Küstenschutz soll vom Punkt  aus eine geradlinige Buhnenreihe senkrecht zur Küstenlinie von Festland I gebaut werden. Zeige, dass die Buhnenreihe auf dem Graphen der Funktion
aus eine geradlinige Buhnenreihe senkrecht zur Küstenlinie von Festland I gebaut werden. Zeige, dass die Buhnenreihe auf dem Graphen der Funktion  mit
mit 
 liegt.
liegt.
Die Buhnenreihe soll ins Meer hineinragen.
ins Meer hineinragen.
Bestimme in diesem Sachzusammenhang den kleinstmöglichen Definitionsbereich von
Die Buhnenreihe soll
Bestimme in diesem Sachzusammenhang den kleinstmöglichen Definitionsbereich von
Erreichbare BE-Anzahl: 06
1.5
Der Verlauf der Küstenlinie von Festland II wird durch den Graphen der Funktion  mit
mit 
 beschrieben. Ein Motorboot befindet sich im Punkt
beschrieben. Ein Motorboot befindet sich im Punkt  der Küstenlinie von Festland I. Das Motorboot soll auf dem kürzesten Weg zu Küstenlinie von Festland II gelangen.
der Küstenlinie von Festland I. Das Motorboot soll auf dem kürzesten Weg zu Küstenlinie von Festland II gelangen.
Bestimmt die Länge dieses kürzesten Weges.
Ermittle die Koordinaten des Punktes, in dem das Motorboot auf die Küstenlinie von Festland II trifft.
Bestimmt die Länge dieses kürzesten Weges.
Ermittle die Koordinaten des Punktes, in dem das Motorboot auf die Küstenlinie von Festland II trifft.
Erreichbare BE-Anzahl: 06
1.6
Im Laufe der Zeit hat sich der Verlauf der Küstenlinie von Festland I verändert. Vor einiger Zeit verlief die Küstenlinie von Festland I durch den Punkt  Bestimme den Parameter
Bestimme den Parameter  so, dass der Graph der zugehörigen Funktion
so, dass der Graph der zugehörigen Funktion  die damalige Küstenlinie von Festland I beschreibt.
die damalige Küstenlinie von Festland I beschreibt.
Erreichbare BE-Anzahl: 03
1.7
Durch die sich ändernde Küstenlinie von Festland I wurden in den letzten 100 Jahren bis zum gegenwärtigen Zeitpunkt  Festland im Bereich
Festland im Bereich  an das Meer verloren.
an das Meer verloren.
Bestimme den Parameter der Funktion
der Funktion  deren Graph die Küstenlinie vor 100 Jahren beschreibt.
deren Graph die Küstenlinie vor 100 Jahren beschreibt.
Es gibt eine Fähre, die ausschließlich von Fußgängern und Radfahrern genutzt wird. Der Anteil der Fußgänger an allen Nutzern der Fähre beträgt Bestimme den Parameter
Erreichbare BE-Anzahl: 05
1.8
Es werden 100 Nutzer der Fähre zufällig ausgewählt.
Berechne die Wahrscheinlichkeiten der folgenden Ereignisse unter Annahme einer Binomialverteilung:
Berechne die Wahrscheinlichkeiten der folgenden Ereignisse unter Annahme einer Binomialverteilung:
Ereignis A:
Mehr als die Hälfte dieser Nutzer der Fähre sind Radfahrer.
Ereignis B:
Es sind weniger Fußgänger unter diesen Nutzern der Fähre als zu erwarten sind.
Erreichbare BE-Anzahl: 05
1.9
Ein Ticket für Fußgänger kostet  und ein Ticket für Radfahrer
und ein Ticket für Radfahrer  Andere Tickets werden nicht angeboten. Für den Fährbetrieb fallen pro Tag
Andere Tickets werden nicht angeboten. Für den Fährbetrieb fallen pro Tag  Betriebskosten an. Im Mittel sind täglich
Betriebskosten an. Im Mittel sind täglich  Nutzer der Fähre zu erwarten.
Nutzer der Fähre zu erwarten.
Berechne den mittleren Verlust der Fährbetreiber an einem Tag.
Der mittlere Verlust soll durch eine Erhöhung der Ticketpreise ausgeglichen werden. Dabei soll das Verhältnis der Tickepreise für Fußgänger und Radfahrer erhalten bleiben. Es wird davon ausgegangen, dass weiterhin im Mittel täglich Nutzer der Fähre zu erwarten sind.
Nutzer der Fähre zu erwarten sind.
Berechne um welchen Betrag der jeweilige Ticketpreis mindestens angehoben werden muss.
Berechne den mittleren Verlust der Fährbetreiber an einem Tag.
Der mittlere Verlust soll durch eine Erhöhung der Ticketpreise ausgeglichen werden. Dabei soll das Verhältnis der Tickepreise für Fußgänger und Radfahrer erhalten bleiben. Es wird davon ausgegangen, dass weiterhin im Mittel täglich
Berechne um welchen Betrag der jeweilige Ticketpreis mindestens angehoben werden muss.
Erreichbare BE-Anzahl: 07
1.10
Die Vermutung, dass der Anteil der Radfahrer an allen Fährkunden am Wochenende  beträgt, soll mithilfe eines zweiseitigen Signifikanztests überprüft werden. Dazu werden
beträgt, soll mithilfe eines zweiseitigen Signifikanztests überprüft werden. Dazu werden  Nutzer der Fähre zufällig ausgewählt und ermittelt, ob die Fußgänger oder Radfahrer sind. Die Nullhypothese „Der Anteil der Radfahrer am Wochenende beträgt
Nutzer der Fähre zufällig ausgewählt und ermittelt, ob die Fußgänger oder Radfahrer sind. Die Nullhypothese „Der Anteil der Radfahrer am Wochenende beträgt  “ soll überprüft werden.
“ soll überprüft werden.
Von den zufällig ausgewählten und befragten Nutzern der Fähre waren
zufällig ausgewählten und befragten Nutzern der Fähre waren  Radfahrer.
Radfahrer.
Untersuche, ob aus diesen Daten die Nullhypothese auf einem Signifikanzniveau von abgelehnt werden muss.
abgelehnt werden muss.
Von den
Untersuche, ob aus diesen Daten die Nullhypothese auf einem Signifikanzniveau von
Erreichbare BE-Anzahl: 04
1.1
Koordinaten des lokalen Maximumpunkts angeben
Mit dem CAS können die Koordinaten des Hochpunkts wie folg bestimmt werden:
 TI nspire CAS
TI nspire CAS
 Casio Classpad II
Der Taschenrechner liefert
Casio Classpad II
Der Taschenrechner liefert  Wendepunkt zeigen
1. Schritt: Notwendiges Kriterium nachweisen
Für eine Wendestelle
Wendepunkt zeigen
1. Schritt: Notwendiges Kriterium nachweisen
Für eine Wendestelle  von
von  muss gelten
muss gelten  Das notwendige Kriterium für Wendestellen ist also für
Das notwendige Kriterium für Wendestellen ist also für  erfüllt.
2. Schritt: Hinreichendes Kriterium überprüfen
Gilt zusätzlich zum notwendigen Kriterium auch
erfüllt.
2. Schritt: Hinreichendes Kriterium überprüfen
Gilt zusätzlich zum notwendigen Kriterium auch  so handelt es sich bei
so handelt es sich bei  um eine Wendestelle von
um eine Wendestelle von 
![\(\begin{array}[t]{rll}
f_2‘‘(x) &=& 12\cdot x - 18 \\[5pt]
f_2‘‘‘(x) &=& 12 \\[10pt]
f_2‘‘‘(1,50) &=& 12\neq 0 \\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/318bcd7f78afa653d2ddaa818252ecabae50052ba817641575b71f58ede064cb_light.svg) Bei
Bei  handelt es sich also um eine Wendestelle von
handelt es sich also um eine Wendestelle von  3. Schritt: Zweite Koordinate nachweisen
Der Punkt
3. Schritt: Zweite Koordinate nachweisen
Der Punkt  ist also ein Wendepunkt des Graphen von
ist also ein Wendepunkt des Graphen von 
menu  6: Graph analysieren
6: Graph analysieren  3: Maximum
3: Maximum
Analyse  Grafische Lösung
Grafische Lösung  Maximum
Maximum
1.2
Schnittwinkel bestimmen
1. Schritt: Koordinaten von  bestimmen
bestimmen
 liegt auf dem Graphen von
liegt auf dem Graphen von  und auf der
und auf der  -Achse.
-Achse.
![\(\begin{array}[t]{rll}
f_2(0)&=& 2\cdot 0^3 -9\cdot 0^2 +12\cdot 0 - 2 \\[5pt]
&=& -2
\end{array}\)](https://www.schullv.de/resources/formulas/78a1044a71d3bd632459674bd921890a83b9c0a891ef593a721ffd734e5ff4ab_light.svg) Der Punkt
Der Punkt  hat also die Koordinaten
hat also die Koordinaten  2. Schritt: Schnittwinkel bestimmen
Mit den Punkten
2. Schritt: Schnittwinkel bestimmen
Mit den Punkten 
 und der
und der  -Achse kann ein rechtwinkliges Dreieck gebildet werden, mit dessen Hilfe der gesuchte Winkel bestimmt werden kann.
-Achse kann ein rechtwinkliges Dreieck gebildet werden, mit dessen Hilfe der gesuchte Winkel bestimmt werden kann.
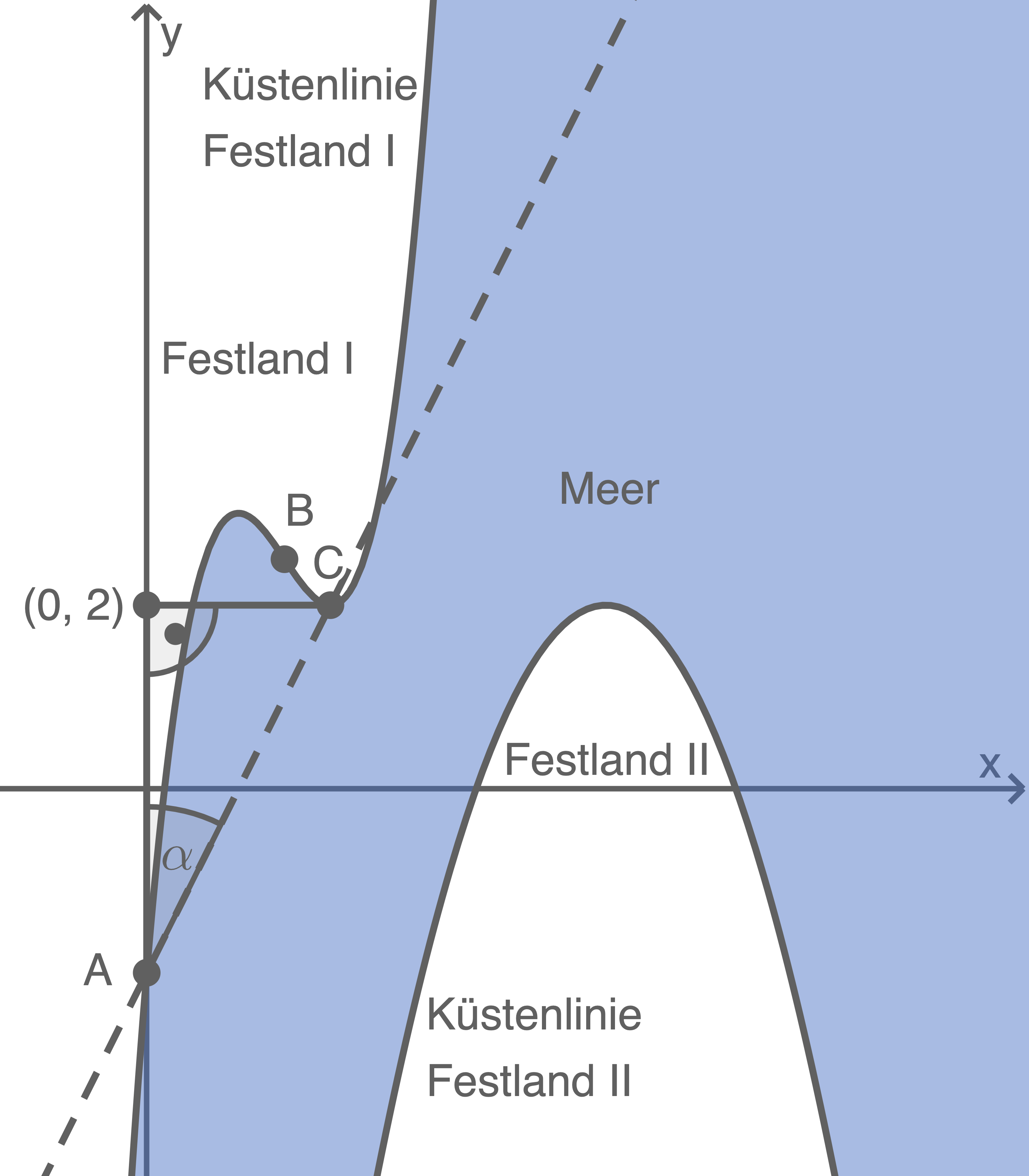 Die Ankathete zum gesuchten Winkel
Die Ankathete zum gesuchten Winkel  hat die Länge
hat die Länge  die Gegenkathete hat die Länge
die Gegenkathete hat die Länge  Mit dem Tangens ergibt sich nun für
Mit dem Tangens ergibt sich nun für 
![\(\begin{array}[t]{rll}
\tan \alpha &=& \dfrac{2}{4} &\quad \scriptsize \mid\; \tan^{-1} \\[5pt]
\alpha &\approx& 27^{\circ} \\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/b738d67a7e94ac1f46f6cc724bb81cb2420b18ab083a0ad597aa095f5fae6a6d_light.svg) Der Schnittwinkel der Geraden durch
Der Schnittwinkel der Geraden durch  und
und  mit der Ordinatenachse ist ca.
mit der Ordinatenachse ist ca.  groß.
groß.

Skizze
1.3
Länge des Wegs ermitteln
Die Länge des Strandwanderweges von  bis
bis  kann über die Bogenlänge des Graphen von
kann über die Bogenlänge des Graphen von  von
von  bis
bis  berechnet werden. Mit der entsprechenden Formel gilt:
berechnet werden. Mit der entsprechenden Formel gilt:
 TI nspire CAS
TI nspire CAS
 Casio Classpad II
Der CAS lieftert
Casio Classpad II
Der CAS lieftert ![\(s[A,C] \approx 6,66\,\text{[km]}.\)](https://www.schullv.de/resources/formulas/6a622557dde8bc19d9cc24f260696398329fa75780485d311e0883c83ffe7bb0_light.svg) Der Strandweg von
Der Strandweg von  nach
nach  ist ca.
ist ca.  lang.
Koordinaten des Zielpunkts ermitteln
Es kann wieder die gleiche Formel wie oben angewendet werden. Die
lang.
Koordinaten des Zielpunkts ermitteln
Es kann wieder die gleiche Formel wie oben angewendet werden. Die  -Koordinate von
-Koordinate von  ist die obere Integrationsgrenze
ist die obere Integrationsgrenze  Es muss also folgende Gleichung nach
Es muss also folgende Gleichung nach  aufgelöst werden.
Systematisches Ausprobieren mit dem CAS liefert die folgenden Werte:
Die
aufgelöst werden.
Systematisches Ausprobieren mit dem CAS liefert die folgenden Werte:
Die  -Koordinate von
-Koordinate von  ist also ca.
ist also ca.  Die zugehörige
Die zugehörige  -Koordinate ist dann:
Die Koordinaten von
-Koordinate ist dann:
Die Koordinaten von  sind ca.
sind ca. 
menu  4: Analysis
4: Analysis  3: Integral
3: Integral
keyboard  Math2
Math2 

1.4
Lage auf dem Graphen zeigen
Die Buhnenreihe liegt auf der Normalen zum Graphen von  im Punkt
im Punkt  Die Steigung der Normalen kann aus der Steigung der Tangente an den Graphen von
Die Steigung der Normalen kann aus der Steigung der Tangente an den Graphen von  im Punkt
im Punkt  berechnet werden.
berechnet werden.
Die Tangente hat die gleiche Steigung wie der Graph von im Punkt
im Punkt  also:
also:
![\(\begin{array}[t]{rll}
m_t &=& f_2‘(1,50) \\[5pt]
&=& 6\cdot 1,50^2 -18\cdot 1,50 +12 \\[5pt]
&=& -1,50 \\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/7154922e807119c9aa0535c419267e6f501fe99f9a2ba45e3956ff7ff41d48dc_light.svg) Für die Steigung der Normalen
Für die Steigung der Normalen  gilt:
gilt:
![\(\begin{array}[t]{rll}
m_n &=& -\dfrac{1}{m_t} \\[5pt]
&=& -\dfrac{1}{-1,50} \\[5pt]
&=& \dfrac{2}{3}
\end{array}\)](https://www.schullv.de/resources/formulas/5242e6cb32cb8ec5f727757f4cd52000ed06c2ae387e370f456e982d234b4fe9_light.svg) Die Normale soll durch den Punkt
Die Normale soll durch den Punkt  verlaufen:
verlaufen:
![\(\begin{array}[t]{rll}
n: \, y &=& m_n \cdot x +b_n \\[5pt]
y &=& \dfrac{2}{3} \cdot x +b_n \quad \scriptsize \mid\; B(1,50\mid 2,50) \\[5pt]
2,50 &=& \dfrac{2}{3}\cdot 1,50 +b_n \\[5pt]
2,50 &=& 1 +b_n \quad \scriptsize \mid\;-1 \\[5pt]
1,50 &=& b_n\\[5pt]
\dfrac{3}{2} &=& b_n
\end{array}\)](https://www.schullv.de/resources/formulas/9a2d0fe02e8c8565ad1746ff042b894e631de762dd9e8cea005119af67e663bf_light.svg) Die Normale zum Graphen von
Die Normale zum Graphen von  im Punkt
im Punkt  besitzt also die Gleichung
besitzt also die Gleichung  Kleinstmöglichen Definitionsbereich angeben
Die Grenzen des Definitionsbereichs von
Kleinstmöglichen Definitionsbereich angeben
Die Grenzen des Definitionsbereichs von  bilden der Anfangspunkt
bilden der Anfangspunkt  und der Endpunkt
und der Endpunkt  der Buhnenreihe.
der Buhnenreihe.
Der Endpunkt soll
soll  von
von  entfernt auf der Geraden
entfernt auf der Geraden  liegen. Er hat also Koordinaten der Form
liegen. Er hat also Koordinaten der Form  Der Abstand von
Der Abstand von  und
und  soll
soll  beantragen. Mit der Formel für den Abstand zweier Punkte ergibt sich folgende Gleichung:
Der solve-Befehl des CAS liefert folgende Lösungen:
beantragen. Mit der Formel für den Abstand zweier Punkte ergibt sich folgende Gleichung:
Der solve-Befehl des CAS liefert folgende Lösungen:
![\(\begin{array}[t]{rll}
x_1&\approx& 1,44 \\[5pt]
x_2 &\approx& 1,56
\end{array}\)](https://www.schullv.de/resources/formulas/d92fe01dcc4cf1e5527fdba48c80a3f0cb62ff627659e78df085c2d03c71c395_light.svg) Im Fall von
Im Fall von  würde das zweite Ende der Buhnenreihe auf dem Festland liegen, die Buhnenreihe soll aber in das Meer hineinragen, nicht ins Festland. Also kommt nur
würde das zweite Ende der Buhnenreihe auf dem Festland liegen, die Buhnenreihe soll aber in das Meer hineinragen, nicht ins Festland. Also kommt nur  als
als  -Koordinate für das zweite Ende der Buhnenreihe infrage. Der kleinstmögliche Definitionsbereich von
-Koordinate für das zweite Ende der Buhnenreihe infrage. Der kleinstmögliche Definitionsbereich von  im Sachzusammenhang ist daher:
im Sachzusammenhang ist daher:

Die Tangente hat die gleiche Steigung wie der Graph von
Der Endpunkt
1.5
Länge des kürzesten Weges bestimmen
Der Ankunftspunkt  liegt auf dem Graphen der Funktion
liegt auf dem Graphen der Funktion  und hat daher Koordinaten der Form
und hat daher Koordinaten der Form  Der Abstand zwischen
Der Abstand zwischen  und
und  kann wie im letzten Aufgabenteil nun durch folgenden Funktionsterm beschrieben werden:
kann wie im letzten Aufgabenteil nun durch folgenden Funktionsterm beschrieben werden:
 beschreibt nun den Abstand zwischen dem Punkt
beschreibt nun den Abstand zwischen dem Punkt  und dem Graphen von
und dem Graphen von  Das Minimum von
Das Minimum von  im Bereich
im Bereich  kann mit dem CAS bestimmt werden.
kann mit dem CAS bestimmt werden.
 TI nspire CAS
TI nspire CAS
 Casio Classpad II
Der Taschenrechner liefert
Casio Classpad II
Der Taschenrechner liefert  Der kürzeste Weg ist also ca.
Der kürzeste Weg ist also ca.  lang.
Koordinaten des Ankunftspunktes ermitteln
Die
lang.
Koordinaten des Ankunftspunktes ermitteln
Die  -Koordinate des Ankunftspunktes
-Koordinate des Ankunftspunktes  wurde oben bereits bestimmt, sie lautet
wurde oben bereits bestimmt, sie lautet  Die zugehörige
Die zugehörige  -Koordinate ergibt sich durch Einsetzen in den Funktionsterm von
-Koordinate ergibt sich durch Einsetzen in den Funktionsterm von 
![\(\begin{array}[t]{rll}
g(4,00)&=& -4,00^2+10\cdot 4,00 -23 \\[5pt]
&=& 1,00
\end{array}\)](https://www.schullv.de/resources/formulas/aec5e31f4dac123967c2f6a5f930bd78f039d8fe6fc552d222d39b464e5f2f2c_light.svg) Der Ankunftspunkt am Festland
Der Ankunftspunkt am Festland  hat die Koordinaten
hat die Koordinaten 
menu  6: Graph analysieren
6: Graph analysieren  2: Minimum
2: Minimum
Analyse  Grafische Lösung
Grafische Lösung  Minimum
Minimum
1.6
1.7
Der Graph von  beschreibt den Verlauf des Festlands
beschreibt den Verlauf des Festlands  heute, der Graph der gesuchten Funktion
heute, der Graph der gesuchten Funktion  beschreibt den Verlauf des Festlands
beschreibt den Verlauf des Festlands  vor
vor  Jahren.
Jahren.
Das verloren gegangene Land entspricht der Fläche zwischen dem Graphen von und
und  im Bereich
im Bereich 
Gesucht ist also sodass der Flächeninhalt dieser Fläche
sodass der Flächeninhalt dieser Fläche  beträgt. Der Flächeninhalt kann mithilfe eines Integrals in Abhängigkeit von
beträgt. Der Flächeninhalt kann mithilfe eines Integrals in Abhängigkeit von  bestimmt werden:
Der Graph der Funktion
bestimmt werden:
Der Graph der Funktion  mit
mit  beschreibt die Küstenlinie vor
beschreibt die Küstenlinie vor  Jahren.
Jahren.
Das verloren gegangene Land entspricht der Fläche zwischen dem Graphen von
Gesucht ist also
1.8
Die Zufallsgröße  beschreibt die zufällige Anzahl der Radfahrer unter den
beschreibt die zufällige Anzahl der Radfahrer unter den  zufällig ausgewählten Nutzern der Fähre.
zufällig ausgewählten Nutzern der Fähre.  ist binomialvertielt mit
ist binomialvertielt mit  und
und 
Die gesuchten Wahrscheinlichkeiten können mit dem CAS berechnet werden.
 TI nspire CAS
TI nspire CAS
 Casio Classpad II
Casio Classpad II
![\(\begin{array}[t]{rll}
P(A) &=& P(X\gt 50) \\[5pt]
&=& 1- P(X\leq 50)\quad \scriptsize \mid\; \text{CAS} \\[5pt]
&\approx& 1-0,9998 \\[5pt]
&=& 0,0002\\[5pt]
&=& 0,02 \,\%\\[10pt]
\end{array}\)](https://www.schullv.de/resources/formulas/d67688fa566053e431332f78c84d17b79866f6806b8c61638c4a48c12d131f30_light.svg) Zu erwarten ist, dass
Zu erwarten ist, dass  aller Nutzer Fußgänger sind, also
aller Nutzer Fußgänger sind, also  Gesucht ist also die Wahrscheinlichkeit dafür, dass höchstens
Gesucht ist also die Wahrscheinlichkeit dafür, dass höchstens  Fußgänger unter den zufällig ausgewählten Nutzern sind. Dies entspricht der Wahrscheinlichkeit dafür, dass mindestens
Fußgänger unter den zufällig ausgewählten Nutzern sind. Dies entspricht der Wahrscheinlichkeit dafür, dass mindestens  Radfahrer unter den zufällig ausgewählten Nutzern sind.
Radfahrer unter den zufällig ausgewählten Nutzern sind.
![\(\begin{array}[t]{rll}
P(B) &=& P(X\geq 34) \\[5pt]
&=& 1- P(X\leq 33) \quad \scriptsize \mid\; \text{CAS} \\[5pt]
&\approx& 1-0,5188 \\[5pt]
&=& 0,4812\\[5pt]
&=& 48,12\,\%\\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/d78c3c608b0181adb9df72591f1217cda74b55b96ed3d144908a3e0c8a4fef36_light.svg)
Die gesuchten Wahrscheinlichkeiten können mit dem CAS berechnet werden.
menu  5
5  5
5  E: Binomial Cdf
E: Binomial Cdf
Interaktiv  Verteilungsfunktionen
Verteilungsfunktionen  Diskret
Diskret  binomial CDf
binomial CDf
1.9
Mittleren Verlust pro Tag berechnen
Im Mittel sind an einem Tag  Nutzer zu erwarten. Davon sind
Nutzer zu erwarten. Davon sind  Fußgänger und
Fußgänger und  Radfahrer.
Anzahl Fußgänger, die zu erwarten sind:
Radfahrer.
Anzahl Fußgänger, die zu erwarten sind: 
Anzahl Radfahrer, die zu erwarten sind: Erwartete Einnahmen an einem Tag:
Erwartete Einnahmen an einem Tag:
 Der Fährbetreiber nimmt am Tag im Mittel
Der Fährbetreiber nimmt am Tag im Mittel  ein. Er macht also
ein. Er macht also  Verlust.
Betrag der Erhöhung pro Ticket berechnen
Das Verhältnis der Ticketpreis soll erhalten bleiben. Im Folgenden werden die neuen Ticketpreis für Fußgänger mit
Verlust.
Betrag der Erhöhung pro Ticket berechnen
Das Verhältnis der Ticketpreis soll erhalten bleiben. Im Folgenden werden die neuen Ticketpreis für Fußgänger mit  und die für Radfahrer mit
und die für Radfahrer mit  bezeichnet. Es soll also gelten:
bezeichnet. Es soll also gelten:
 Die neuen Ticketpreise sollen mindestens die Betriebskosten von
Die neuen Ticketpreise sollen mindestens die Betriebskosten von  abdecken, die jeden Tag anfallen. Die Einnahmen, die der Fährbetrieb im Mittel an einem Tag hat, sollen also
abdecken, die jeden Tag anfallen. Die Einnahmen, die der Fährbetrieb im Mittel an einem Tag hat, sollen also  betragen. Es folgt daher folgende Gleichung in Abhängigkeit der neuen Preise:
betragen. Es folgt daher folgende Gleichung in Abhängigkeit der neuen Preise:
 Die erste Gleichung lässt sich beispielsweise nach
Die erste Gleichung lässt sich beispielsweise nach  umformen:
umformen:
![\(\begin{array}[t]{rll}
\dfrac{p_F}{p_R} &=& \dfrac{1,85\,€ }{3,70\,€} \quad \scriptsize \mid\; \cdot p_R\\[5pt]
p_F &=& \dfrac{1,85\,€ }{3,70\,€}\cdot p_R \\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/542e00945a7325ef553efbec986a6d0192085e0f331247e476a79bf176427b70_light.svg) Dies kann in die zweite Gleichung eingesetzt werden.
Für Fußgänger gilt also:
Dies kann in die zweite Gleichung eingesetzt werden.
Für Fußgänger gilt also:
![\(\begin{array}[t]{rll}
p_F &=& \dfrac{1,85\,€ }{3,70\,€}\cdot p_R \\[5pt]
&=& \dfrac{1,85\,€ }{3,70\,€}\cdot 4,00\,€\\[5pt]
&=& 2,00\,€
\end{array}\)](https://www.schullv.de/resources/formulas/8900b79c55341f25a08bd62d398a0c95485a73cd1d602090df53615ab3e51c3f_light.svg) Der Ticketpreis für Fußgänger muss also mindestens um
Der Ticketpreis für Fußgänger muss also mindestens um  und der Preis für Radfahrer um
und der Preis für Radfahrer um  erhöht werden, um die Betriebskosten pro Tag zu decken.
erhöht werden, um die Betriebskosten pro Tag zu decken.
Anzahl Radfahrer, die zu erwarten sind:
1.10
Betrachtet wird die Zufallsgröße  die in der Stichprobe von
die in der Stichprobe von  zufällig ausgewählten Nutzern die zufällige Anzahl der Radfahrer beschreibt. Diese kann als binomialverteilt mit
zufällig ausgewählten Nutzern die zufällige Anzahl der Radfahrer beschreibt. Diese kann als binomialverteilt mit  und unbekanntem
und unbekanntem  angenommen werden. Geht man davon aus, dass
angenommen werden. Geht man davon aus, dass  entsprechend der Nullhypothese
entsprechend der Nullhypothese
 „Der Anteil der Radfahrer am Wochenende beträgt
„Der Anteil der Radfahrer am Wochenende beträgt  “
verteilt ist, so ist
“
verteilt ist, so ist  Gesucht ist nun ein Annahmebereich
Gesucht ist nun ein Annahmebereich  der symmetrisch um den Erwartungswert von
der symmetrisch um den Erwartungswert von  ist. Für diesen soll aufgrund des Sginifikanzniveaus gelten:
ist. Für diesen soll aufgrund des Sginifikanzniveaus gelten:
![\(\begin{array}[t]{rll}
&P(Y \in \overline{A})&\leq& 0,05 \\[5pt]
\Leftrightarrow &P(Y \in A)&\geq& 0,95
\end{array}\)](https://www.schullv.de/resources/formulas/41c18fbffb187c353f655efffff5a1ce96f080c51b11be838a7205169be7db90_light.svg) Mithilfe der Sigma-Regeln ergibt sich:
Mithilfe der Sigma-Regeln ergibt sich:

 Für
Für  gilt mithilfe der entsprechenden Formeln für eine binomialverteilte Zufallsgröße:
gilt mithilfe der entsprechenden Formeln für eine binomialverteilte Zufallsgröße:



 Damit ergibt sich:
Der Annahmebereich für die Nullhypothese ist also
Damit ergibt sich:
Der Annahmebereich für die Nullhypothese ist also ![\(A=[61;79].\)](https://www.schullv.de/resources/formulas/4ab37973ab536adfc279d43d000074230173910c9521da69a2d780f83bd705ff_light.svg) Die Anzahl der Radfahrer in der Stichprobe betrug
Die Anzahl der Radfahrer in der Stichprobe betrug  Dieser Wert fällt in den Annahmebereich. Die Nullhypothese muss auf einem Signifikanzniveau von
Dieser Wert fällt in den Annahmebereich. Die Nullhypothese muss auf einem Signifikanzniveau von  also nicht abgelehnt werden.
also nicht abgelehnt werden.
Bildnachweise [nach oben]
© - SchulLV.