Aufgabe B1

Bei einem Talentwettbewerb werden die Darbietungen unter anderem mithilfe der Applausstärke bewertet. Dazu wird die Applausstärke gemessen und in Punkten angegeben. Die zeitliche Entwicklung der Applausstärke jeder Darbietung wird durch eine Funktion beschrieben.

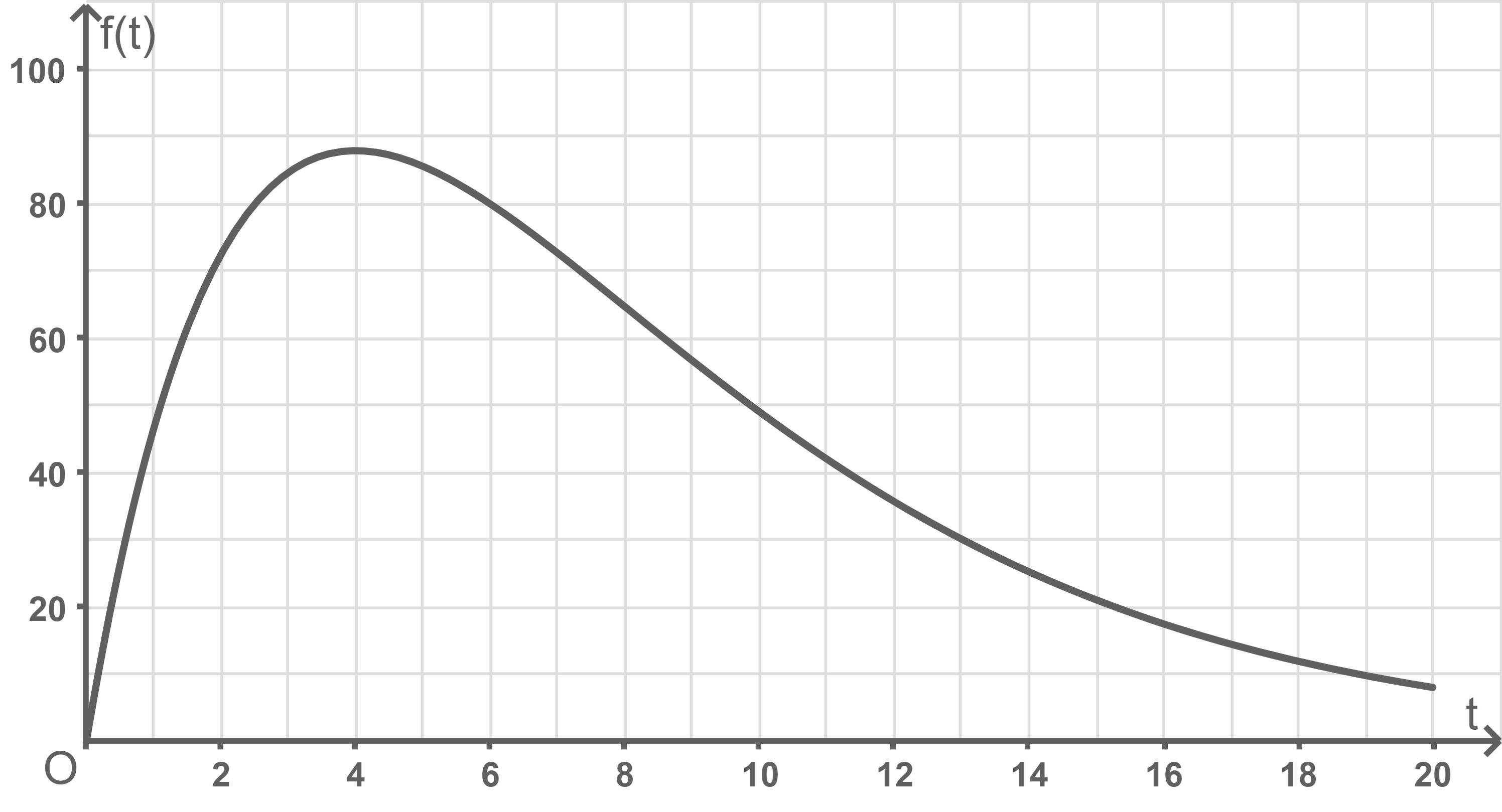
Die Applausstärke der ersten Darbietung wird für $0 \leq t \leq 20$ durch die in $\mathbb{R}$ definierte Funktion $f$ mit $f(t)=40 \cdot t \cdot \mathrm{e}^{-\frac{1}{4} \cdot t+\frac{2}{5}}$ beschrieben. Dabei beschreibt $t$ die seit dem Beginn des Applauses vergangene Zeit in Sekunden und $f(t)$ die Applausstärke in Punkten. Abbildung 1 zeigt den Graphen von $f.$

Abbildung 1

1.1

Ermittle grafisch in Abbildung 1 die Länge des Zeitraums, in dem die Applausstärke mindestens $60$ Punkte beträgt.

(2 BE)

1.2

Es gibt einen Zeitpunkt, zu dem die Applausstärke am größten ist.
Gib diesen Zeitpunkt und den zugehörigen Wert der Applausstärke an.

(2 BE)

1.3

Bestimme denjenigen Zeitpunkt, zu dem die Applausstärke am stärksten abnimmt.
Ermittle grafisch die zugehörige Änderungsrate in Abbildung 1.

(4 BE)

Die Applausstärke der zweiten Darbietung wird für $0 \leq t \leq 20$ durch die in $\mathbb{R}$ definierte Funktion $g$ mit $g(t)=(10 \cdot t-10) \cdot \mathrm{e}^{-\frac{3}{5} \cdot t+\frac{3}{2}}$ $+10 \cdot \mathrm{e}^{\frac{3}{2}}$ beschrieben. Dabei beschreibt $t$ die seit dem Beginn des Applauses vergangene Zeit in Sekunden und $g(t)$ die Applausstärke in Punkten.

1.4

Es gelte: $g\left(t_1\right)=g\left(t_2\right)$ mit $t_2-t_1=10.$
Deute diese Bedingung im Sachzusammenhang.
Ermittle $t_1$ und $t_2.$

(4 BE)

1.5

Es gibt einen Zeitpunkt, zu dem der Unterschied der Applausstärken der ersten beiden Darbietungen maximal ist.
Ermittle diesen maximalen Unterschied.

(4 BE)

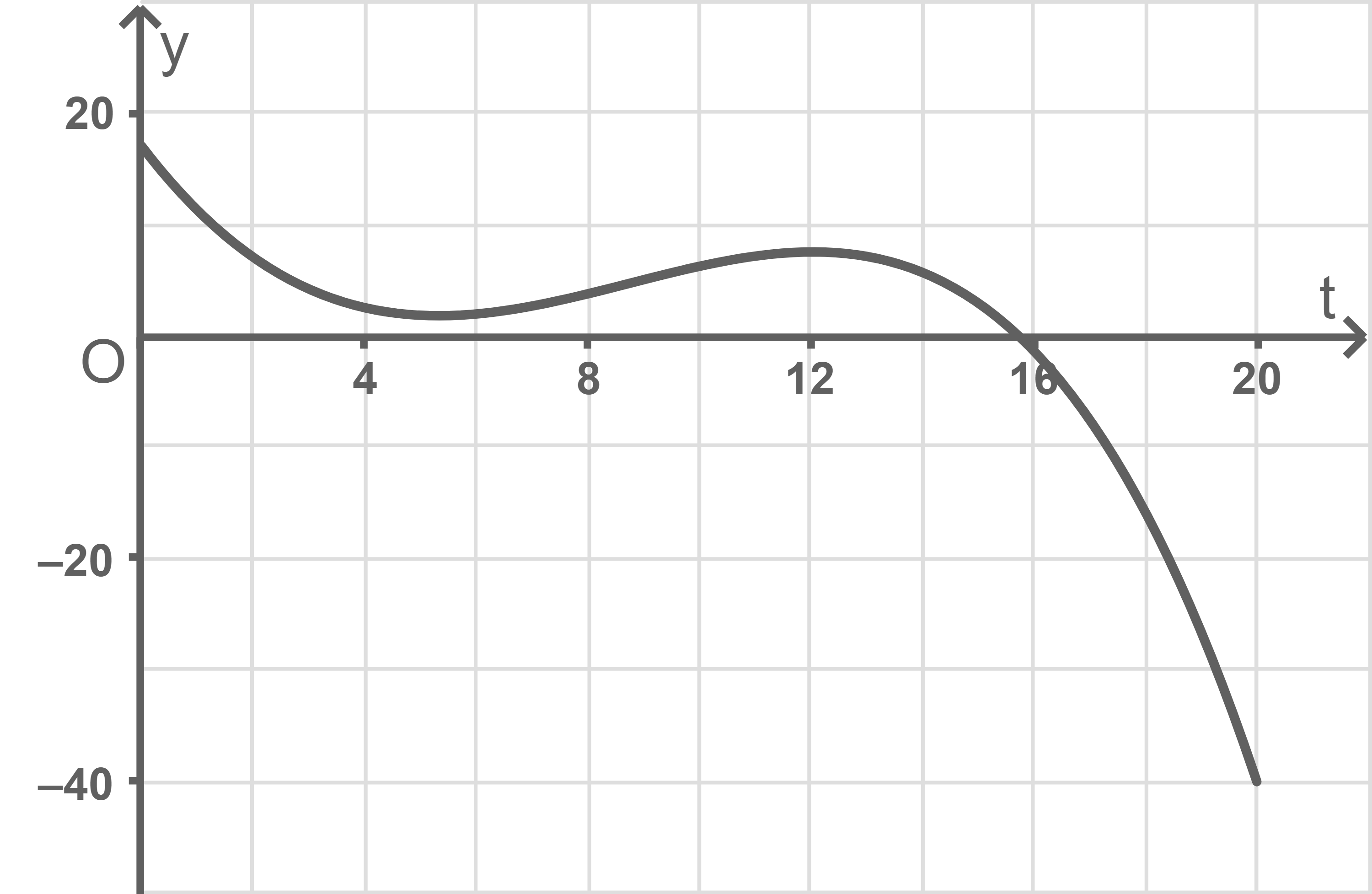
Der in Abbildung 2 dargestellte Graph gibt für die dritte Darbietung die Änderungsrate der Applausstärke in Abhängigkeit von der Zeit $t$ mit $0 \leq t \leq 20$ an. Dabei beschreibt $t$ die seit dem Beginn des Applauses vergangene Zeit in Sekunden.

Abbildung 2

1.6

Beurteile die folgenden Aussagen für die dritte Darbietung.

$(1)$

Das Maximum der Applausstärke tritt nach etwa 12 Sekunden ein.

$(2)$

In den letzten 5 Sekunden der Messung nimmt die Applausstärke um mehr als 100 Punkte ab.

(4 BE)

Gegeben ist die in $\mathbb{R}$ definierte Funktion $w_{a, b}$ mit

$w_{a, b}(x)=-a \cdot \cos \left(\frac{\pi \cdot x}{b}\right)+a$ $\quad(a, b \in \mathbb{R} ; a, b>0) .$

1.7

Gib die Koordinaten eines Hochpunkts des Graphen von $w_{a, b}$ für $a=3$ und $b=\pi$ an.

(2 BE)

1.8

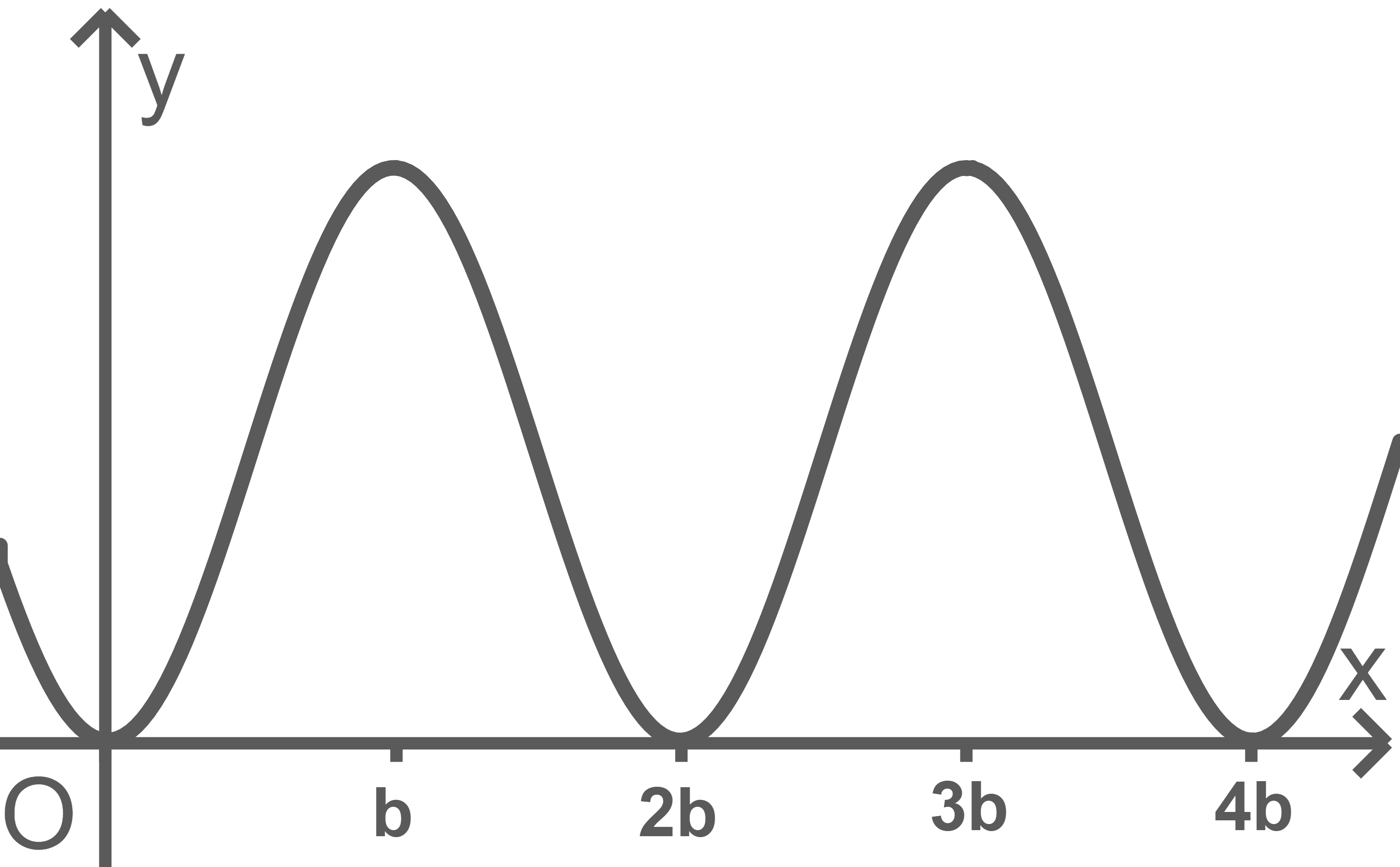
Skaliere in Abbildung 3 die $y$ -Achse so, dass der Graph von $w_{a, b}$ dargestellt ist.
Begründe die vorhandene Skalierung für die $x$ -Achse.

Abbildung 3

(4 BE)

1.9

Gib den Wert des Integrals $\displaystyle\int_{0}^{b}w_{a, b}(x)\;\mathrm dx$ an, ohne den Term einer Stammfunktion von $w_{a,b}$ zu berechnen.
Begründe deine Angabe und veranschauliche deine Überlegungen in Abbildung 3.

(4 BE)

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?

1.1

Die Länge des gesuchten Zeitraums beträgt etwas mehr als sieben Sekunden.

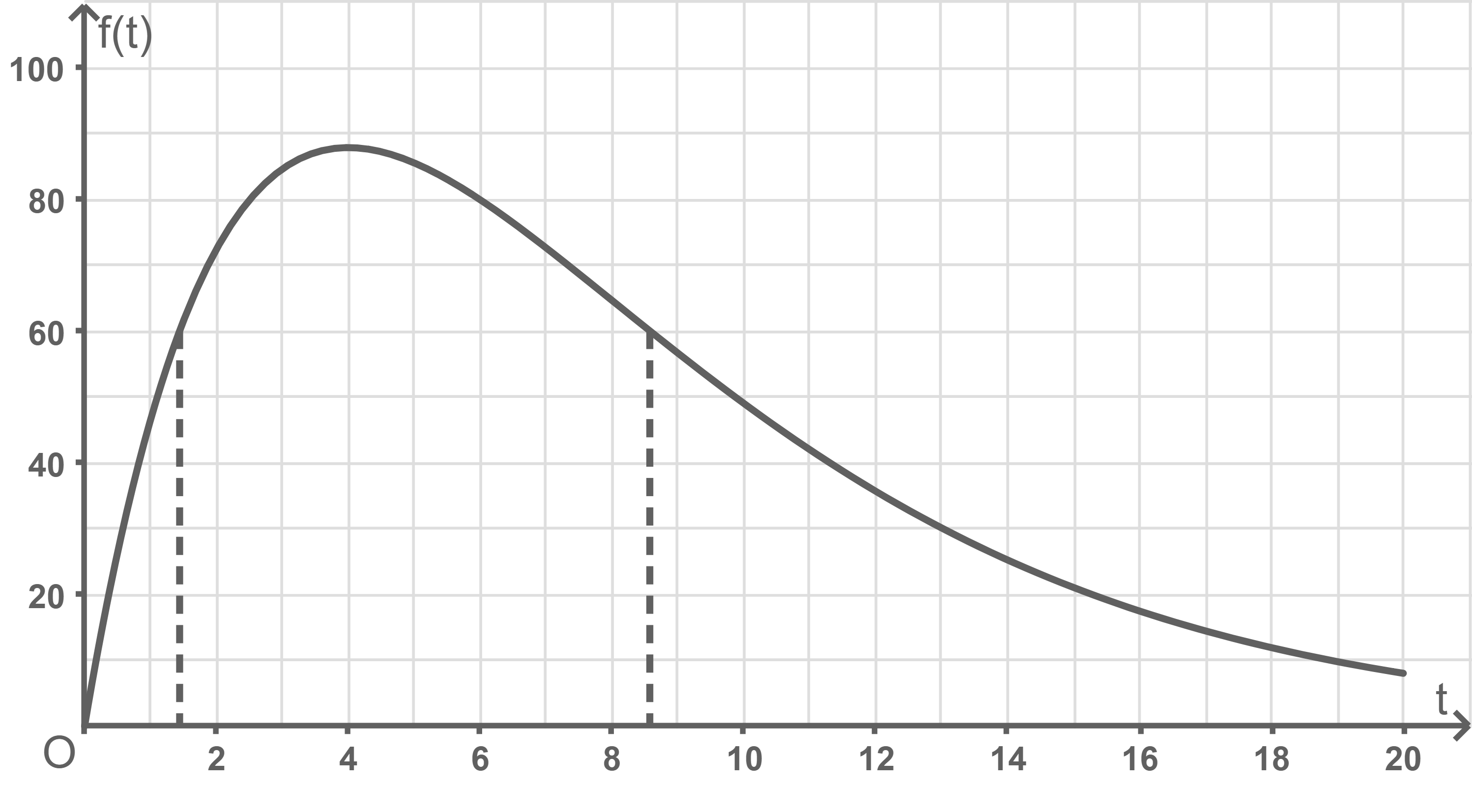
1.2

Aus der Abbildung folgt, dass die Applausstärke nach vier Sekunden am stärksten ist und etwa $88$ Punkte beträgt.

1.3

Zeitpunkt der stärksten Abnahme bestimmen

Für die ersten beiden Ableitungen von $f$ folgt mit dem MMS:

$\(f$

Anwenden der notwendigen Bedingung $\(f$ für Wendestellen liefert mit dem solve-Befehl des MMS:

$t=8$

Mit Hilfe der Abbildung folgt, dass an dieser Stelle die Rechtskrümmung des Graphen in eine Linkskrümmung übergeht. Somit ist $t=8$ die gesuchte Wendestelle und es kann auf die Überprüfung der hinreichenden Bedingung verzichtet werden.
Die Applausstärke nimmt damit nach $8$ Sekunden am stärksten ab.

Änderungsrate graphisch ermitteln

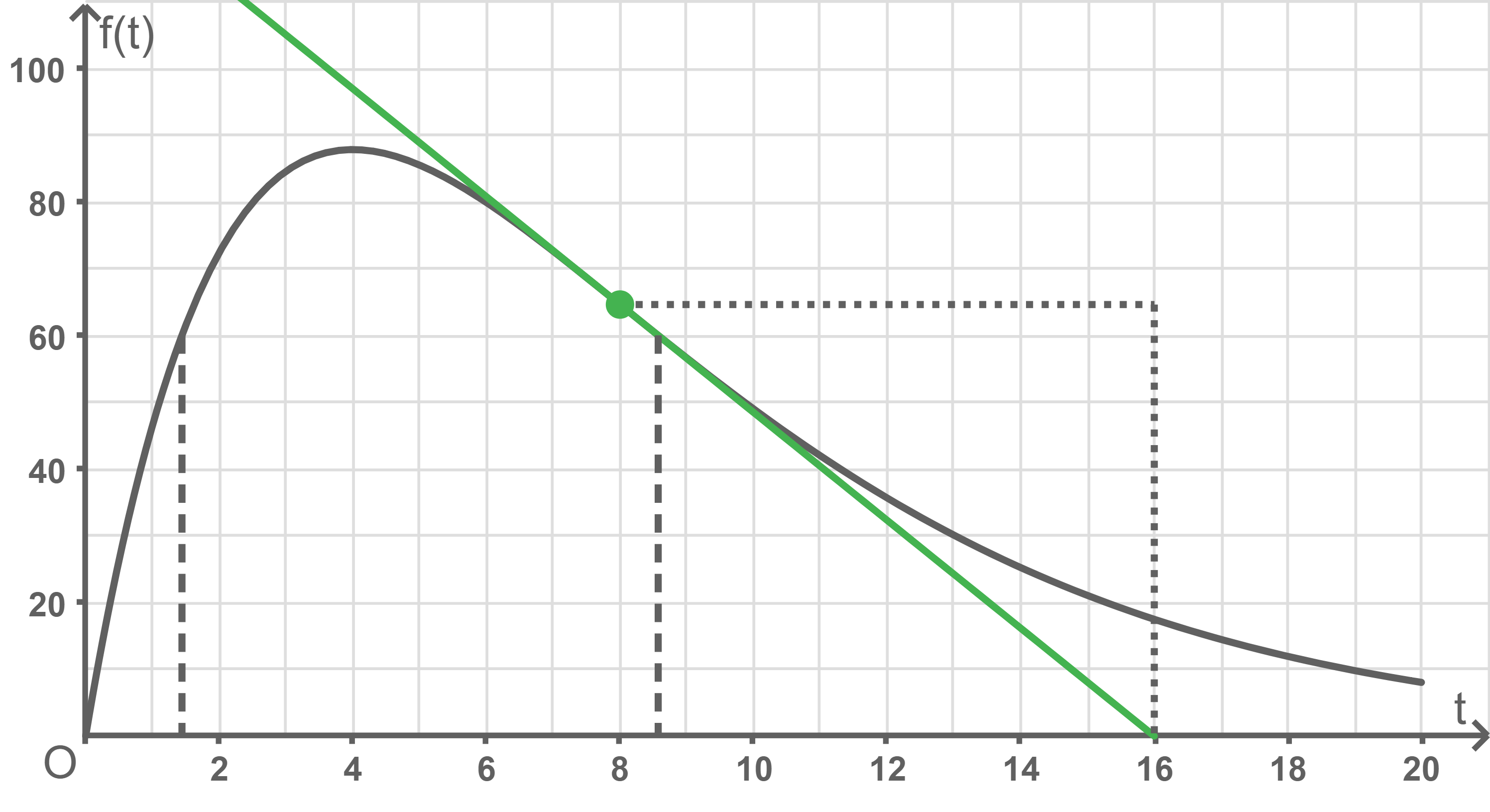Die Änderungsrate beträgt somit ca. $-\frac{64}{8}=-8$ Punkte pro Sekunde.

1.4

Bedingung im Sachzusammenhang deuten

Betrachtet werden zwei Zeitpunkte in der zweiten Darbietung, die $10$ Sekunden auseinander liegen und bei denen die Applausstärke gleichviele Punkte beträgt.

$\boldsymbol{t_1}$ und $\boldsymbol{t_2}$ ermitteln

Laut Aufgabenstellung gilt $t_2-t_1=10$ bzw. $t_1+10=t_2.$ Damit folgt:

Rechenweg anzeigen

$(10t_1-10) \cdot \mathrm{e}^{-\frac{3}{5}t_1+\frac{3}{2}}$ $= (10t_1+90) \cdot \mathrm{e}^{-\frac{3}{5}t_1-\frac{9}{2}}$

Mit dem solve-Befehl des CAS folgt:

$t_1\approx1$

Somit ergeben sich die beiden gesuchten Zeitpunkte als $t_1\approx1$ und $t_2\approx1+10=11.$

1.5

Für die Differenzenfunktion gilt:

Differenzenfunktion anzeigen

Für die ersten beiden Ableitungen folgt mit dem MMS:

Ableitungen anzeigen

1. Schritt: Notwendige Bedingung für Extremstellen anwenden

$\(d$

Mit dem solve-Befehl des MMS folgt:

$\begin{array}[t]{rlll} t_1&\approx&0,4 \\[5pt] t_2&\approx&4,7 \end{array}$

2. Schritt: Hinreichende Bedingung für Extremstellen überprüfen

Einsetzen von $t_1$ und $t_2$ in $\(d$ liefert mit dem MMS $\(d$ und $\(d$ Somit liegt jeweils eine Extremstelle vor. Da nur der maximale Unterschied gefragt ist, ist es egal ob es ein Tiefpunkt oder Hochpunkt ist.

3. Schritt: Funktionswerte bestimmen

Einsetzen von $t_1$ und $t_2$ in $d$ liefert mit dem MMS:

$\begin{array}[t]{rlll} d(0,4)&\approx&-2,1 \\[5pt] d(4,7)&=&31,9 \end{array}$

Für die Werte von $d$ an den Intervallgrenzen liefert der MMS:

$\begin{array}[t]{rlll} d(0)&=&0 \\[5pt] d(20)&\approx&-36,8 \end{array}$

Der maximale Unterschied ergibt sich also durch den Betrag des Funktionswertes von $d$ bei $t=20,$ da dieser größer ist als die Werte an den beiden Extrempunkten.
Der maximale Unterschied der Applausstärken der ersten beiden Darbietungen beträgt somit etwa $36,8$ Punkte.

1.6

Aussage $(1)$ ist falsch, denn der Graph gibt nicht die Applausstärke an, sondern die Änderungsrate dieser. Das Maximum der Applausstärke ist somit in der Nullstelle mit Vorzeichenwechsel von plus nach minus, welche nicht bei $t=12$ liegt.
Die Abnahme der Applausstärke in den letzten fünf Sekunden ergibt sich durch den Inhalt des Flächenstücks, welches der Graph für $15 \leq t \leq 20$ mit der $t$ -Achse einschließt. Der Inhalt dieses Flächenstücks ist kleiner als $\frac{5 \cdot 40}{2}=100.$ Somit ist Aussage $(2)$ ebenfalls falsch.

1.7

$H(\pi \mid 6)$

1.8

$\boldsymbol{y}$ -Achse skalieren

Da der Kosinus mit dem Faktor $-a$ multipliziert wird, und um $a$ in $y$ -Richtung verschoben wird, besitzen die Hochpunkte von $w_{a,b}(x)$ den $y$ -Wert $2a.$ Somit folgt:

Skalierung begründen

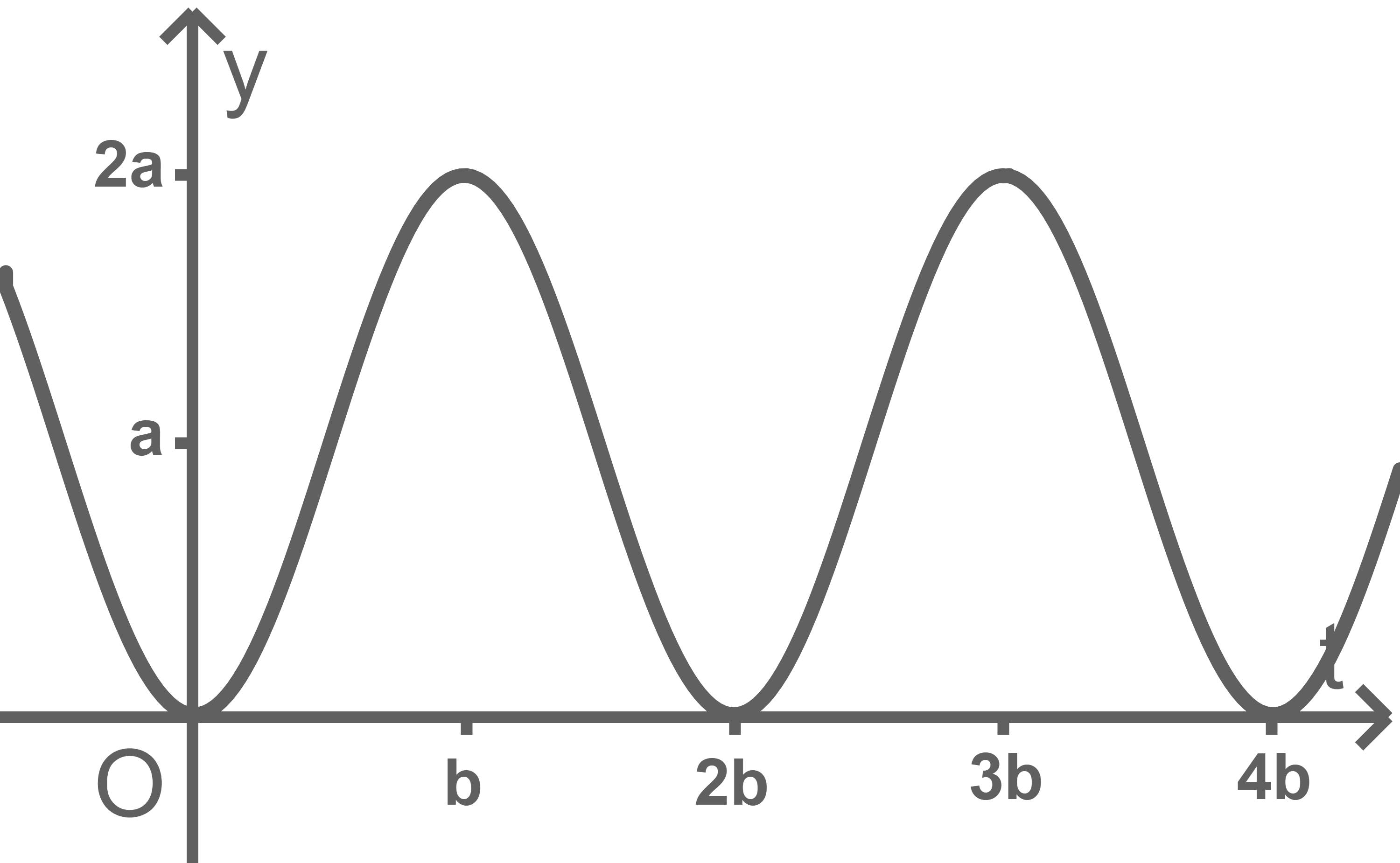
Die kleinste Periode des Kosinus beträgt $2\pi.$ Somit folgt für die kleinste Periode von $w_{a,b}:$

$\dfrac{2\pi}{\frac{\pi}{b}}=2b$

Damit ergibt die Skalierung der $x$ -Achse Sinn.

1.9

Der Graph von $w_{a,b}$ ist Punktsymmetrisch zu jedem Wendepunkt, also auch insbesondere zum Punkt $\left(\frac{b}{2}\mid a\right).$ Somit halbiert der Graph von $w_{a,b}$ das folgende Rechteck:

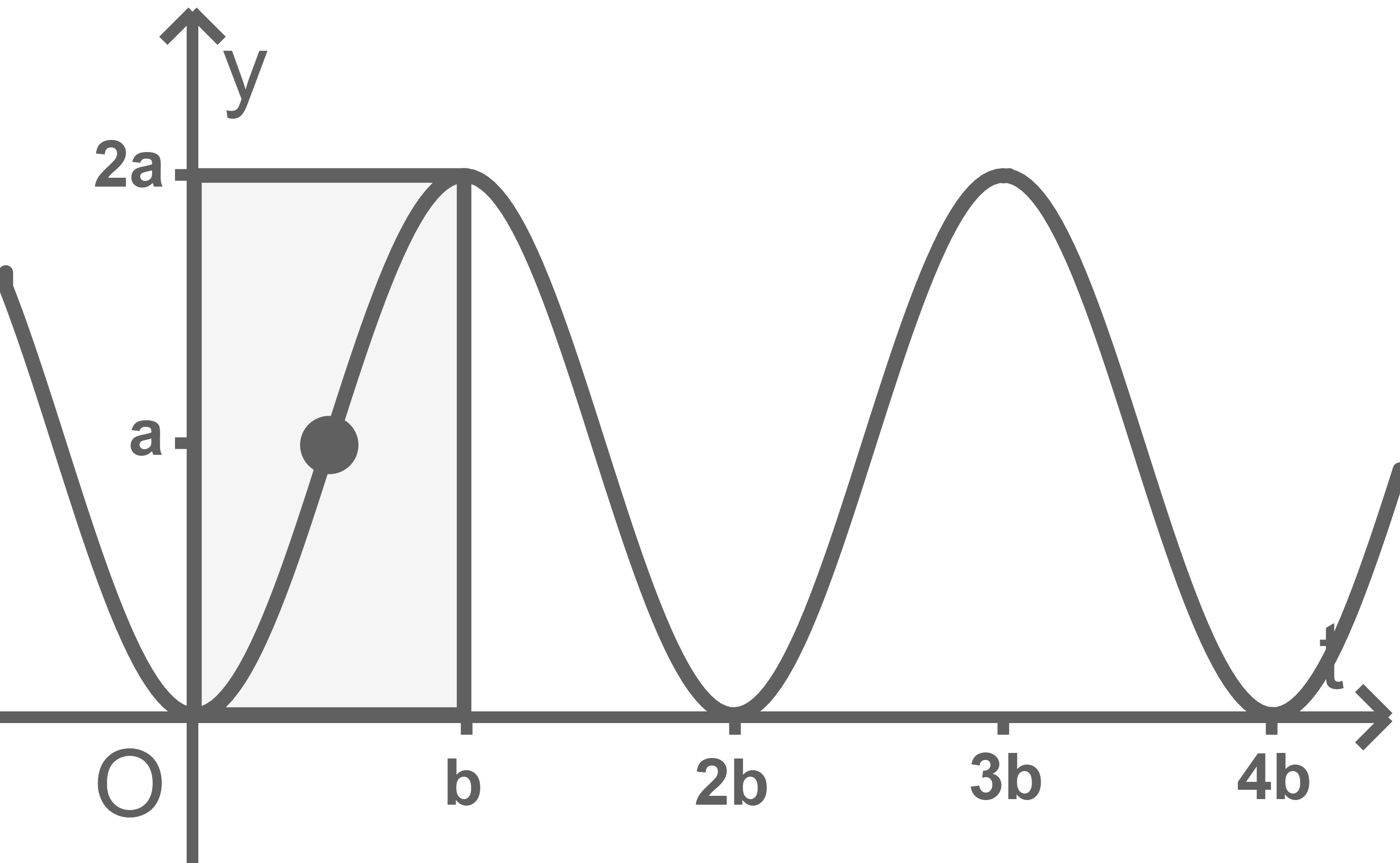Der Wert des gesuchten Integrals ergibt sich somit als die Hälfte des Flächeninhalts des Rechtecks mit den Seitenlängen $2a$ und $b:$

$\displaystyle\int_{0}^{b}w_{a,b}(x)\;\mathrm dx=\frac{1}{2}\cdot2a\cdot b=ab$

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?