Aufgabe B2

Die Punkte $A(6\mid0\mid 0), B(6\mid7\mid 0),$ $C(0\mid7\mid 0)$ , $D(0\mid0\mid 0),$ $E(4\mid2\mid 5), F(4\mid9\mid 5),$ $G$ und $H(-2\mid2\mid 5)$ sind die Eckpunkte des Prismas $A B C D E F G H$ , dessen sechs Seitenflächen jeweils Parallelogramme sind (vgl. Abbildung 4).

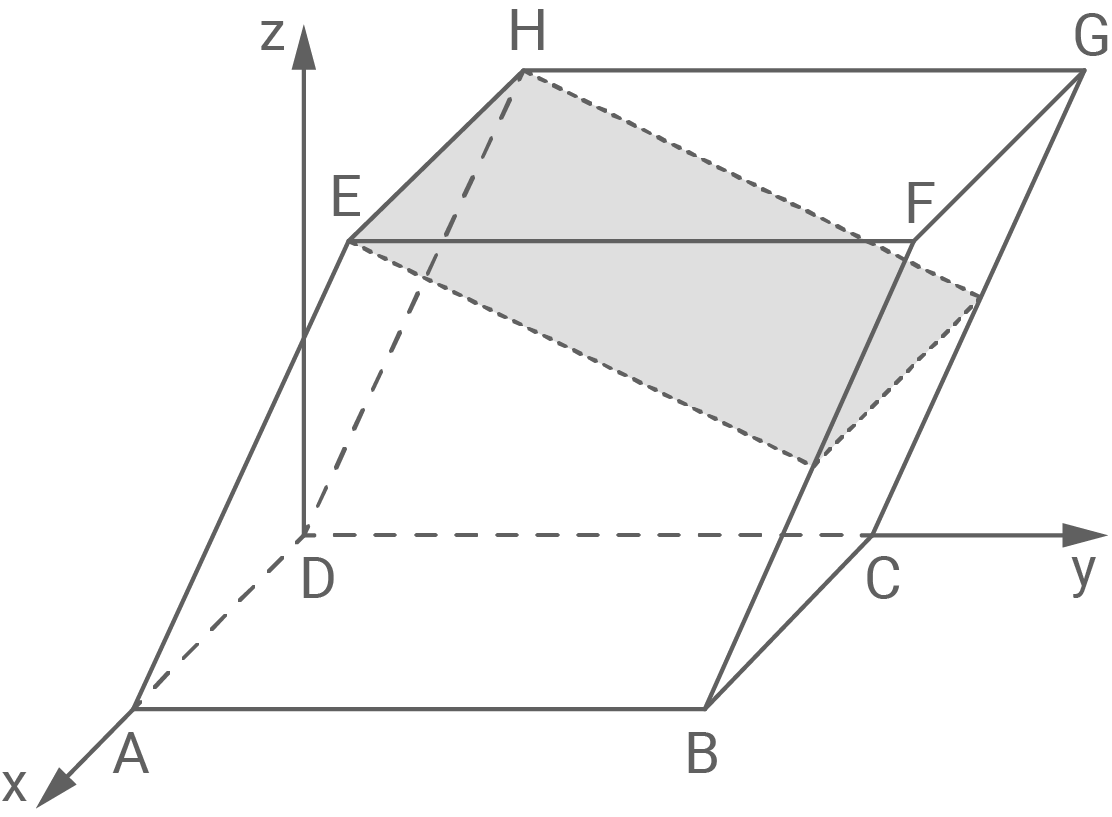
Abbildung 4

2.1

Gib die Koordinaten von $G$ an.
Begründe, dass die Seitenfläche $DCGH$ nicht in der $y$ - $z$ -Ebene liegt.

(4 BE)

2.2

Zur Berechnung einer Größe im Zusammenhang mit dem Prisma wird der Term $2 \cdot(\vert\overrightarrow{A B} \times \overrightarrow{A E}\vert+\vert\overrightarrow{A B} \times \overrightarrow{A D}\vert$ $+\vert\overrightarrow{A E} \times \overrightarrow{A D}\vert)$ verwendet.
Gib die Größe an, die damit berechnet werden kann.
Begründe deine Angabe.

(2 BE)

Für jeden reellen Wert von $t$ ist eine Ebene $\varepsilon_t:(5-5 \cdot t) \cdot y$ $+(5+2 \cdot t) \cdot z=35$ gegeben.

2.3

Ermittle alle Werte $t,$ für die der Winkel zwischen $\varepsilon_0$ und $\varepsilon_t$ eine Größe von $45^{\circ}$ hat.

(3 BE)

2.4

Begründe, dass die Gerade durch $E$ und $H$ in allen Ebenen $\varepsilon_t$ liegt.
Gib alle Eckpunkte des Prismas an, die in $\varepsilon_0$ liegen.
Zeige, dass $\varepsilon_1$ parallel zur $x$ - $y$ -Ebene verläuft.
In Abbildung 4 ist ein Ausschnitt der Ebene $\varepsilon_t$ dargestellt, welche die Mittelpunkte der Kanten $\overline{BF}$ und $\overline{CG}$ enthält.
Ermittle den zugehörigen Wert $t.$

(7 BE)

2.5

Für $0 \leq t\lt1$ teilt $\varepsilon_t$ das Prisma jeweils in zwei Teilkörper. Der Teilkörper, der den Punkt $F$ enthält, hat das Volumen $V_1,$ der andere Teilkörper das Volumen $V_2.$ Die Funktion $v$ mit $v(t)=\frac{V_1(t)}{V_2(t)}$ ordnet jedem Wert von $t$ mit $0 \leq t\lt1$ das Verhältnis der beiden Volumina zu. Genau einer der Graphen in Abbildung 5 stellt den Graphen von $v$ dar.
Gib den Graphen an, der den Graphen von $v$ darstellt.
Begründe für jeden der beiden anderen Graphen, dass er nicht den Graphen von $v$ darstellt.

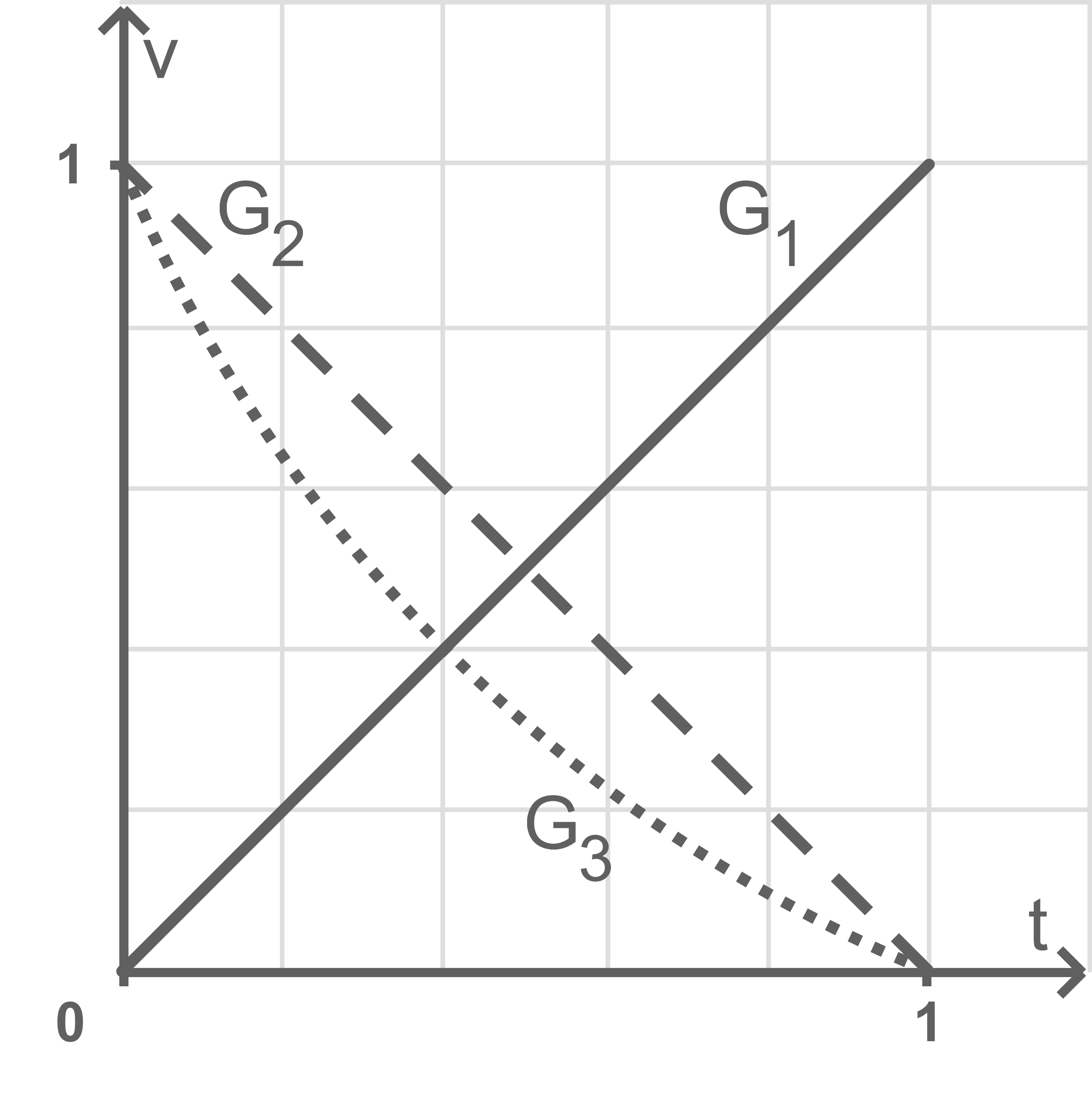
Abbildung 5

(4 BE)

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?

2.1

Koordinaten von $\boldsymbol{G}$ angeben

Abbildung 4 zeigt, dass die Punkte $E, F, G$ und $H$ dieselbe $z$ Koordinate besitzen, sowie die $x$ - Koordinate von $G$ der von $H$ entspricht und die $y$ -Koordinate der von $F$ entspricht. Somit folgt:

$G(-2\mid9\mid5)$

Lage der Seitenfläche $\boldsymbol{DCGH}$ begründen

Die $y$ - $z$ -Ebene besitzt die Ebenengleichung $x=0.$ Da der Punkt $H$ die $x$ -Koordinate $-2$ besitzt, liegt die Seitenfläche somit nicht in dieser Ebene.

2.2

Der Betrag des Kreuzprodukts zweier Vektoren gibt den Flächeninhalt des von ihnen aufgespannten Parallelogramms an. Der Term aus der Aufgabenstellung gibt somit den Oberflächeninhalt des Prismas $ABCDEFGH$ an, da die Oberfläche aus sechs Seitenflächen besteht, von denen die jeweils gegenüberliegenden Flächen gleichgroß sind.

2.3

Ablesen des Normalenvektors aus der Ebenengleichung der Ebene $\varepsilon_t$ liefert:

$\pmatrix{0\\5-5t\\5+2t}$

Damit folgt:

Rechenweg anzeigen

$\cos(45^\circ)=\dfrac{10-3t}{\sqrt{100-60t+58t^2}}$

Mit dem solve-Befehl des MMS folgt für die gesuchten Werte von $t:$

$\begin{array}[t]{rlll} t_1&=&-\dfrac{5}{2} \\[5pt] t_2&=&1 \end{array}$

2.4

Lage der Geraden durch $\boldsymbol{E}$ und $\boldsymbol{H}$ begründen

Einsetzen der Koordinaten von $E$ in die Ebenengleichung von $\varepsilon_t$ liefert:

$\begin{array}[t]{rlll} (5-5t)\cdot2+(5+2t)\cdot5&=&35 \\[5pt] 10-10t+25+10t&=&35 \\[5pt] 35&=&35 \end{array}$

Mit den Koordinaten von $H$ folgt:

$\begin{array}[t]{rlll} (5-5t)\cdot2+(5+2t)\cdot5&=&35 \\[5pt] 10-10t+25+10t&=&35 \\[5pt] 35&=&35 \end{array}$

Somit liegen sowohl $E$ als auch $H$ in $\varepsilon_t$ und damit auch die Gerade die durch diese beiden Punkte verläuft.

Eckpunkte angeben

Eine Ebenengleichung von $varepsilon_0$ ist gegeben durch $\varepsilon_0:5y+5z=35.$

Dass die beiden Punkte $E$ und $H$ in $\varepsilon_0$ liegen, ist bereits bekannt. Einsetzen der Koordinaten von $B$ in die Ebenengleichung liefert:

$\begin{array}[t]{rlll} 5\cdot7+5\cdot0&=&35 \\[5pt] 35&=&35 \end{array}$

Da der Punkt $C$ die selben $y$ - und $z$ -Koordinaten aufweist, liegt somit sowohl $B$ als auch $C$ in $\varepsilon_0.$ Mit Hilfe von Abbildung $4$ folgt, dass $B, C, G$ und $H$ alle Eckpunkte des Prismas sind, die in der Ebene $\varepsilon_0$ liegen.

Parallelität von $\boldsymbol{\varepsilon_1}$ zur $\boldsymbol{x}$ - $\boldsymbol{y}$ -Ebene zeigen

Für eine Ebenengleichung von $\varepsilon_1$ folgt:

$\varepsilon_1:7z=35$

Da diese Ebenengleichung nur von $z$ abhängt, verläuft $\varepsilon_1$ parallel zur $x$ - $y$ -Ebene.

Wert von $\boldsymbol{t}$ ermitteln

Für den Mittelpunkt $M$ der Kante $\overline{BF}$ gilt:

$\begin{array}[t]{rlll} \overrightarrow{OM}&=&\overrightarrow{OB}+\dfrac{1}{2}\cdot\overrightarrow{BF} \\[5pt] &=&\pmatrix{6\\7\\0}+\dfrac{1}{2}\cdot\pmatrix{4-6\\9-7\\5-0} \\[5pt] &=&\pmatrix{5\\8\\2,5} \end{array}$

Einsetzen der Koordinaten von $M$ in die Ebenengleichung von $\varepsilon_t$ liefert:

$\begin{array}[t]{rlll} (5-5t)\cdot8+(5+2t)\cdot2,5&=&35 \\[5pt] 40-40t+12,5+5t&=&35 \\[5pt] 52,5-35t&=&35 \end{array}$

Mit dem solve-befehl des MMS folgt für den gesuchten Wert von $t:$

$t=\dfrac{1}{2}$

2.5

Der Graph $G_1$ kann nicht der Graph von $v$ sein, da nach Teilaufgabe 2.4 die Ebene $\varepsilon_0$ das Prisma halbiert, das heißt es muss $v(0)=1$ gelten.
$G_2$ stellt ebenfalls nicht den Graphen von $v$ dar, da aus Teilaufgabe 2.4 bekannt ist, dass $\varepsilon_\frac{1}{2}$ durch den Mittelpunkt der Kante von $\overline{BF}$ verläuft, und $V_1$ somit ein Viertel des Gesamtvolumens des Prismas ausmacht. $G_2$ stellt allerdings $v\left(\frac{1}{2}\right)=\frac{1}{2}$ dar, und nicht $v\left(\frac{1}{2}\right)=\frac{1}{3}.$
Damit stellt $G_3$ den Graphen von $v$ dar.

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?