Teil B2

Zur Tierbeobachtung wird ein Hochstand errichtet (siehe Abbildung).

Der geplante Hochstand besteht aus einer Kanzel, die von einem Kanzelbock getragen wird, einer Leiter und einem Dach.

Der Kanzelbock besteht aus den Balken $\overline{AG}$ , $\overline{BH}$ , $\overline{CI}$ und $\overline{DJ}$ . Die Punkte $A$ , $B$ , $C$ und D bilden ein Rechteck.

Auf die Kanzel $GHMLQPJINOTU$ , welche die Form eines geraden Prismas besitzt, ist das rechteckige Dach $PRSU$ aufgesetzt.

Die rechteckige Leiter $EFKG$ führt vom Boden zum rechteckigen Einstieg $GKVP$ in die Kanzel.

Der geplante Hochstand kann in einem kartesischen Koordinatensystem (1 Längeneinheit entspricht 1 Meter) dargestellt werden. Der ebene Boden liegt dabei in der $x$ - $y$ -Koordinatenebene.

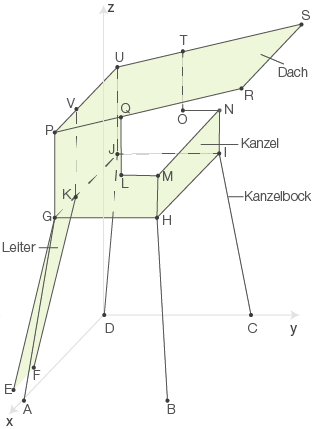3D-Diagramm mit geometrischen Formen und Beschriftungen für eine technische Darstellung.

Abbildung (nicht maßstäblich)

Folgende Punktkoordinaten sind gegeben:
$A(4,0\mid 0,0 \mid 0,0 ),\; C(0,0\mid 3,5\mid 0,0),$ $D(0,0\mid 0,0\mid 0,0),\, G(3,5\mid 0,5\mid 4,0),$ $I(0,5\mid 3,0\mid 4,0),$

$J(0,5\mid 0,5\mid 4,0),\; M(3,5 \mid 3,0\mid 5,0),$ $L(3,5 \mid 2,0\mid 5,0),\; P(3,5\mid 0,5\mid 6,0),$ $S(0,5\mid 4,0\mid 6,7).$
Materialdicken werden vernachlässigt.

2.1

Gebe die Koordinaten des Punktes $O$ an.

(3P)

2.2

Bestimme den Neigungswinkel eines Balkens des Kanzelbocks gegenüber dem Boden.

(4P)

2.3

Die Leiter ist gegenüber dem Boden um etwa $76°$ geneigt.

Ermittle den Abstand des Punktes $E$ vom Punkt $A$ .

(6P)

2.4

Die Kante $\overline{QL}$ verläuft parallel zur $z$ -Achse.

Begründe, dass der Punkt $Q$ die Koordinaten $Q(3,5 \mid 2,0 \mid 6,3)$ besitzt.

(4P)

Zur Stabilisierung des Hochstandes sollen zwischen den Balken des Kanzelbocks geradlinige Streben angebracht werden.

2.5

Parallel zum Boden soll in einer Höhe von $1,0\,$ m eine Strebe zwischen den Balken $\overline{AG}$ und $\overline{DJ}$ angebracht werden.

Ermittle die Länge dieser Strebe.

(4P)

2.6

Von einem Punkt des Balkens $\overline{DJ}$ sollen zwei Streben so an den Endpunkten des Balkens $\overline{CI}$ befestigt werden, dass diese Streben einen rechten Winkel bilden.

Untersuche, ob dies möglich ist.

(7P)

2.7

Zum Verbinden der Teile des Hochstandes werden Nägel verwendet.

Die Länge dieser Nägel ist annähernd normalverteilt. Es wurde festgestellt, dass in $1\,\%$ aller Fälle die Länge dieser Nägel geringer als $85\,$ mm und in $1\,\%$ aller Fälle die Länge dieser Nägel größer als $99\,$ mm sind.

Berechne aus diesen Angaben den Erwartungswert der Länge dieser Nägel und die Standardabweichung.

(6P)

2.8

Zur Einweihung des Hochstandes bereitet dessen Besitzer für Kinder ein Spiel vor. Für dieses Spiel stellt er drei Gefäße $A$ , $B$ und $C$ bereit. In den drei Gefäßen befinden sich gleichartige Lose mit je einem Bild. Folgende Lose befinden sich in den Gefäßen:

Gefäß $A$ : $3$ Lose mit einem Reh, $4$ Lose mit einem Kuckuck

Gefäß $B$ : $1$ Los mit einem Reh, $2$ Lose mit einem Kuckuck

Gefäß $C$ : $5$ Lose mit einem Reh

Als Spielregeln sollen gelten:

Ein Kind zieht zufällig ein Los aus Gefäß $A$ und legt es in Gefäß $B$ . Danach zieht dieses Kind zufällig ein Los aus Gefäß $B$ und legt es in das Gefäß $C$ .
Befindet sich anschließend im Gefäß $C$ ein Los mit einem Kuckuck, gewinnt das Kind.

Ermittle, mit welcher Wahrscheinlichkeit das Kind bei diesem Spiel gewinnt.

(6P)

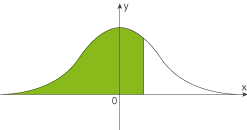
Materialien für Aufgaben zur Stochastik

Verteilungsfunktion der Standardnormalverteilung

$\phi(z)=$	$\dfrac{1}{\sqrt{2\pi}}\mathop{\displaystyle\int}\limits_{-\infty}^{z}\mathrm{e}^{-\frac{1}{2}t^2}\;\mathrm dt$
$\phi(-z)$ =	$1-\phi(z)$

Graph einer Funktion mit einer grünen Fläche unter der Kurve und Achsenbeschriftungen.

	B	C	D	E	F	G	H	I	J	K	L
2
3	z	0	1	2	3	4	5	6	7	8	9
4	0,0	0,5000	0,5040	0,5080	0,5120	0,5160	0,5199	0,5239	0,5279	0,5319	0,5359
5	0,1	0,5398	0,5438	0,5478	0,5517	0,5557	0,5596	0,5636	0,5675	0,5714	0,5753
6	0,2	0,5793	0,5832	0,5871	0,5910	0,5948	0,5987	0,6026	0,6064	0,6103	0,6141
7	0,3	0,6179	0,6217	0,6255	0,6293	0,6331	0,6368	0,6406	0,6443	0,6480	0,6517
8	0,4	0,6554	0,6591	0,6628	0,6664	0,6700	0,6736	0,6772	0,6808	0,6844	0,6879
9	0,5	0,6915	0,6950	0,6985	0,7019	0,7054	0,7088	0,7123	0,7157	0,7190	0,7224
10	0,6	0,7257	0,7291	0,7324	0,7357	0,7389	0,7422	0,7454	0,7486	0,7517	0,7549
11	0,7	0,7580	0,7611	0,7642	0,7673	0,7704	0,7734	0,7764	0,7794	0,7823	0,7852
12	0,8	0,7881	0,7910	0,7939	0,7967	0,7995	0,8023	0,8051	0,8078	0,8106	0,8133
13	0,9	0,8159	0,8186	0,8212	0,8238	0,8264	0,8289	0,8315	0,8340	0,8365	0,8389
14	1,0	0,8413	0,8438	0,8461	0,8485	0,8508	0,8531	0,8554	0,8577	0,8599	0,8621
15	1,1	0,8643	0,8665	0,8686	0,8708	0,8729	0,8749	0,8770	0,8790	0,8810	0,8830
16	1,2	0,8849	0,8869	0,8888	0,8907	0,8925	0,8944	0,8962	0,8980	0,8997	0,9015
17	1,3	0,9032	0,9049	0,9066	0,9082	0,9099	0,9115	0,9131	0,9147	0,9162	0,9177
18	1,4	0,9192	0,9207	0,9222	0,9236	0,9251	0,9265	0,9279	0,9292	0,9306	0,9319
19	1,5	0,9332	0,9345	0,9357	0,9370	0,9382	0,9394	0,9406	0,9418	0,9429	0,9441
20	1,6	0,9452	0,9463	0,9474	0,9484	0,9495	0,9505	0,9515	0,9525	0,9535	0,9545
21	1,7	0,9554	0,9564	0,9573	0,9582	0,9591	0,9599	0,9608	0,9616	0,9625	0,9633
22	1,8	0,9641	0,9649	0,9656	0,9664	0,9671	0,9678	0,9686	0,9693	0,9699	0,9706
23	1,9	0,9713	0,9719	0,9726	0,9732	0,9738	0,9744	0,9750	0,9756	0,9761	0,9767
24	2,0	0,9772	0,9778	0,9783	0,9788	0,9793	0,9798	0,9803	0,9808	0,9812	0,9817
25	2,1	0,9821	0,9826	0,9830	0,9834	0,9838	0,9842	0,9846	0,9850	0,9854	0,9857
26	2,2	0,9861	0,9864	0,9868	0,9871	0,9875	0,9878	0,9881	0,9884	0,9887	0,9890
27	2,3	0,9893	0,9896	0,9898	0,9901	0,9904	0,9906	0,9909	0,9911	0,9913	0,9916
28	2,4	0,9918	0,9920	0,9922	0,9925	0,9927	0,9929	0,9931	0,9932	0,9934	0,9936
29	2,5	0,9938	0,9940	0,9941	0,9943	0,9945	0,9946	0,9948	0,9949	0,9951	0,9952
30	2,6	0,9953	0,9955	0,9956	0,9957	0,9959	0,9960	0,9961	0,9962	0,9963	0,9964
31	2,7	0,9965	0,9966	0,9967	0,9968	0,9969	0,9970	0,9971	0,9972	0,9973	0,9974
32	2,8	0,9974	0,9975	0,9976	0,9977	0,9977	0,9978	0,9979	0,9979	0,9980	0,9981
33	2,9	0,9981	0,9982	0,9982	0,9983	0,9984	0,9984	0,9985	0,9985	0,9986	0,9986
34	3,0	0,9987	0,9987	0,9987	0,9988	0,9988	0,9989	0,9989	0,9989	0,9990	0,9990
35	3,1	0,9990	0,9991	0,9991	0,9991	0,9992	0,9992	0,9992	0,9992	0,9993	0,9993
36	3,2	0,9993	0,9993	0,9994	0,9994	0,9994	0,9994	0,9994	0,9995	0,9995	0,9995
37	3,3	0,9995	0,9995	0,9995	0,9996	0,9996	0,9996	0,9996	0,9996	0,9996	0,9997
38	3,4	0,9997	0,9997	0,9997	0,9997	0,9997	0,9997	0,9997	0,9997	0,9997	0,9998
39	3,5	0,9998	0,9998	0,9998	0,9998	0,9998	0,9998	0,9998	0,9998	0,9998	0,9998
40	3,6	0,9998	0,9998	0,9999	0,9999	0,9999	0,9999	0,9999	0,9999	0,9999	0,9999
41	3,7	0,9999	0,9999	0,9999	0,9999	0,9999	0,9999	0,9999	0,9999	0,9999	0,9999
42	3,8	0,9999	0,9999	0,9999	0,9999	0,9999	0,9999	0,9999	0,9999	0,9999	0,9999
43	3,9	1,0000	1,0000	1,0000	1,0000	1,0000	1,0000	1,0000	1,0000	1,0000	1,0000

Aufgabe B2

2.1

$\blacktriangleright$ Koordinaten von $\boldsymbol{O}$ bestimmen

Der Aufgabenstellung kannst du entnehmen, dass die Kanzel die Form eines geraden Prismas besitzt. Prismen sind Körper, deren sich gegenüberliegende Seitenkanten parallel und gleich lang sind. Da es sich um ein gerades Prisma handelt, sind die Grundlächen $GHMLQP$ und $JINOTU$ nicht zueinander verschoben. Um die Koordinaten von $O$ zu berechnen, verwendest du die Parallelität der Seitenkanten. Die Kanten $LO$ und $GJ$ liegen sich gegenüber, sind also parallel und gleich lang. Die Koordinaten von $O$ bekommst du, indem du zum Ortsvektor zu $L$ den Verbindungsvektor $\overrightarrow{GJ}$ addierst. Im Folgenden ist $\overrightarrow{OO}$ der Ortsvektor zu $O$ :

$\begin{array}[t]{rll} \overrightarrow{OO}&=&\overrightarrow{OL}+\overrightarrow{GJ} &\quad \\[5pt] \end{array}$

Der Ortsvektor $\overrightarrow{OL}$ entspricht in seinen Koordinaten dem Punkt $L$ . Den Vektor $\overrightarrow{GJ}$ erhältst du wie folgt:

$\begin{array}[t]{rll} \overrightarrow{GJ}&=&\overrightarrow{OJ}-\overrightarrow{OG} &\quad \scriptsize \\[5pt] &=& \pmatrix{0,5 \\ 0,5 \\ 4,0}-\pmatrix{3,5 \\ 0,5 \\ 4,0}\\ &=& \pmatrix{-3 \\ 0 \\ 0} \end{array}$

Damit kannst du den Ortsvektor zu $O$ bestimmen:

$\begin{array}[t]{rll} \overrightarrow{OO}&=&\overrightarrow{OL}+\overrightarrow{GJ} &\quad \\[5pt] &=& \pmatrix{3,5 \\ 2,0 \\ 5,0} +\pmatrix{-3 \\ 0 \\ 0}\\ &=& \pmatrix{0,5 \\ 2,0 \\ 5,0} \end{array}$

Der Punkt $O$ hat also die Koordinaten $O(0,5\mid 2,0\mid 5,0)$ .

2.2

$\blacktriangleright$ Neigungswinkel bestimmen

Du sollst den Neigungswinkel zwischen einem der Balken und dem Boden bestimmen. Du kannst die Balken als Vektoren und den Boden als Ebene darstellen. Da der Boden in der $xy$ -Ebene liegt, ist die Koordinatengleichung dieser Ebene:

$E: z=0$

Wähle jetzt einen Balken, bei dem beide Endpunkte angegeben sind und bestimme den Verbindungsvektor. Du kannst zum Beispiel den Balken $AG$ auswählen.

$\begin{array}[t]{rll} \overrightarrow{AG}&=&\overrightarrow{OG}-\overrightarrow{OA} &\quad \\[5pt] &=&\pmatrix{3,5\\ 0,5 \\ 4,0}- \pmatrix{4,0 \\ 0,0 \\ 0,0} &\quad \\[5pt] &=&\pmatrix{-0,5\\ 0,5 \\ 4,0} \end{array}$

Den Schnittwinkel $\alpha$ zwischen der Ebene $E:z=0$ und dem Vektor $\overrightarrow{u}:=\overrightarrow{AG}$ kannst du mit der Sinus-Formel berechnen:

$\sin\alpha= \dfrac{\left|\vec{n}\cdot\vec{u}\right|}{\left|\vec{n}\right|\cdot\left|\vec{u}\right|}$

Bei dem Vektor $\vec{n}$ handelt es sich um einen Normalenvektor der Ebene $E$ .

Da die Ebene in Koordinatenform angegeben ist, kannst du den Normalenvektor direkt ablesen:

$\overrightarrow{n}=\pmatrix{0 \\ 0 \\ 1}$

Setzte im nächsten Schritt die Vektoren in die Formel ein:

$\begin{array}[t]{rll} \sin\alpha&\approx & 0,9847 \end{array}$

Vollständige Lösung anzeigen

Den Winkel $\alpha$ kannst du jetzt mit deinem Taschenrechner bestimmen:

$\alpha=79,964$

Vollständige Lösung anzeigen

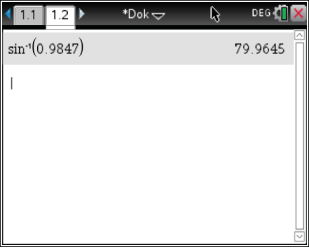Screenshot einer mathematischen Berechnung mit dem Sinus und einem Ergebnis von 79,9645.

Abb. 1: Winkel berechnen mit dem Taschenrechner

Achte darauf, dass dein Taschenrechner auf Degree eingestellt ist.

Der Neigungswinkel zwischen dem Boden und einem Balken des Kanzelblocks beträgt also $79,964° \approx 80°$ .

2.3

$\blacktriangleright$ Abstand zwischen $\boldsymbol{E}$ und $\boldsymbol{A}$ ermitteln

Um den Abstand der beiden Punkte zu berechnen, musst du zuerst die Koordinaten des Punktes $E$ berechnen. Dafür erstellst du dir ein Hilfsdreieck $EZG$ .

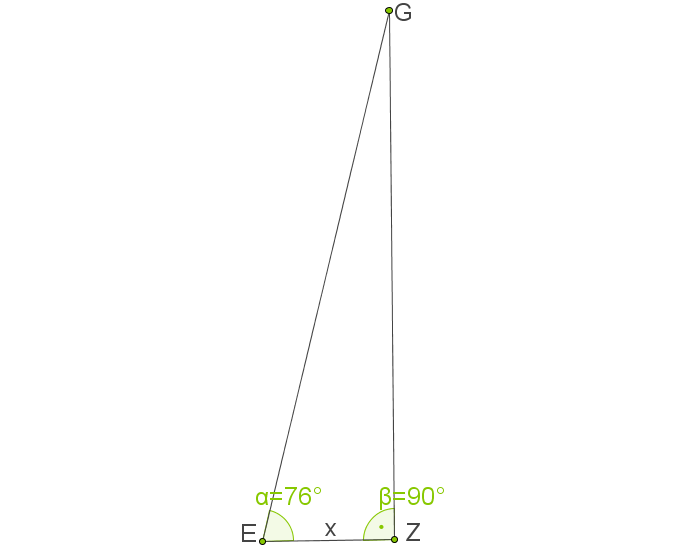Diagramm mit Winkeln α=76° und β=90°, zeigt eine geometrische Beziehung zwischen Punkten E, G und Z.

Abb. 2: Hilfsdreieck

Den Punkt $Z$ wählst du so, dass er senkrecht unter dem Punkt $G$ und in der $xy$ -Ebene liegt. Damit hat $Z$ die Koordinaten $Z(3,5 \mid 0,5 \mid 0)$ . Du kannst alle Größen in diesem Dreieck berechnen, da du den Winkel $\alpha = 76°$ bei $E$ , den rechten Winkel bei $Z$ und die länge der Strecke $|GZ|=4$ bestimmen kannst. Die Länge der Strecke $GZ$ erhältst du, da $G$ und $Z$ bis auf die $z$ - Koordinate übereinstimmen. Damit ist der Abstand der beiden Punkte der Unterschied ihrer $z$ -Koordinaten.

Die Länge der Strecke $x$ kannst du im nächsten Schritt mit dem Tangens bestimmen:

$\begin{array}[t]{rll} \tan(76°)&\approx& 0,997 \end{array}$

Vollständige Lösung anzeigen

Die $y$ - Koordinate von $Z$ ist $0,5$ . Der Abstand von $Z$ zur $x$ -Achse ist also $0,5$ . Die $x$ -Achse ist senkrecht zu der Kante $x$ des Dreiecks $EZG$ . Deswegen ergibt der Abstand von $E$ zur $x$ -Achse zusammen mit dem Abstand von $Z$ zur $x$ -Achse den Abstand von $E$ zu $Z$ und damit der Länge der Kante $x$ aus deinem Dreieck. Mit diesem Wissen kannst du den Abstand von $E$ zur $x-$ Achse berechnen, indem du von der Länge der Kante $x$ den Abstand $0,5$ , von $Z$ zur $x$ -Achse abziehst:

$x-0,5 \approx 0,5$

Vollständige Lösung anzeigen

Da der Abstand von $E$ zur $x$ -Achse $0,5$ ist und $E$ eine negative $y$ -Koordinate besitzt, hat $E$ die $y$ -Koordinate $-0,5$ . Da sowohl Leiter, als auch Einstieg rechteckig sind, müssen $G$ und $E$ die gleiche $x$ -Koordinate haben. Insgesamt hat $E$ also die Koordinaten:

$E(3,5\mid -0,5 \mid 0)$

Jetzt kannst du den Abstand zwischen den Punkten $A$ und $E$ berechnen:

$|AE|=\,\bigg \vert \, \pmatrix{4 \\ 0 \\0} - \pmatrix{3,5 \\ -0,5 \\ 0} \,\bigg \vert \,$ $= \,\bigg \vert \,\pmatrix{0,5 \\ 0,5 \\ 0,5}\,\bigg \vert \,$ $=\sqrt{0,5}$ $\approx 0,7$

Der Abstand des Punktes $E$ vom Punkt $A$ beträgt somit $0,7\text{m}$ .

2.4

$\blacktriangleright$ Koordinaten von $\boldsymbol{Q}$ überprüfen

Du sollst begründen, dass der Punkt $Q$ die Koordinaten $Q(3,5 \mid 2,0 \mid 6,3)$ haben muss. Gehe dazu wie folgt vor:

Bestimme die Koordinaten von $R$ mithilfe der Koordinaten von $P$ und $S$ .
Bestimme die Gleichung der Geraden $g$ , die durch die Punkte $P$ und $R$ verläuft.
Da die Kanzel ein gerades Prisma ist, ist die Kante $LQ$ parallel zu $GP$ und damit senkrecht zur $xy$ -Ebene. Bestimme die Gleichung der Geraden $h$ , die durch $L$ verläuft und senkrecht zur $xy$ -Ebene ist. Diese Gerade verläuft durch $Q$ .
Bestimme den Schnittpunkt von $g$ und $h$ . Dieser Schnittpunkt entspricht dem Punkt $Q$ .

Schritt 1: Koordinaten von $\boldsymbol{R}$ bestimmen

Der Punkt $R$ hat die gleiche $x$ -Koordinate, wie $P$ und stimmt mit $S$ in seiner $y$ - und $z$ -Koordinaten überein. Deswegen hat $R$ die Koordinaten:

$R(3,5 \mid 4,0 \mid 6,7)$

Schritt 2: Gleichung von $g$ bestimmen

Wähle als Stützvektor der Geraden einen der Punkte $P$ oder $R$ und als Spannvektor den Verbindungsvektor $\overrightarrow{PR}$ :

$\overrightarrow{PR}=\pmatrix{3,5 \\ 4,0 \\ 6,7}-\pmatrix{3,5 \\ 0,5 \\ 6,0} =\pmatrix{0 \\ 3,5 \\ 0,7}$

Mit den Koordinaten des Punktes $P$ , als Stützvektor erhältst du:

$g: \overrightarrow{x}= \pmatrix{3,5 \\ 0,5 \\ 6,0}+t\cdot \pmatrix{0 \\ 3,5 \\ 0,7}$

Schritt 3: Gleichung von $h$ bestimmen

Der Stützvektor der Geraden $h$ ist der Ortsvektor zum Punkt $L$ . Der Spannvektor von $h$ entspricht dem Normalenvektor der $xy$ -Ebene und somit

$\overrightarrow{n}=\pmatrix{0 \\0 \\ 1}$

Mit diesen beiden Vektoren kannst du die Geradengleichung aufstellen:

$h: \overrightarrow{x}= \pmatrix{3,5 \\ 2,0 \\ 5,0}+ s \cdot \pmatrix{0 \\ 0 \\ 1}$

Schritt 4: Koordinaten von $\boldsymbol{Q}$ bestimmen

Durch Gleichsetzten der beiden Geradengleichungen erhältst du ein Lineares Gleichungssystem mit drei Gleichungen und zwei Unbekannten:

$\begin{array}{} \text{I}\quad& ...\\ \text{II}\quad& ...\\ \text{III}\quad& ... \end{array}$

Vollständige Lösung anzeigen

Vereinfache die drei Gleichungen zuerst:

$\begin{array}{} \text{I}\quad&3,5&=&3,5\quad \scriptsize\\ \text{II}\quad&3,5 \cdot t&=&1,5 \quad\\ \text{III}\quad&0,7 \cdot t -s&=&-1,0\quad\\ \end{array}$

Gleichung $\text{I}$ liefert dir keine Aussage. Mit Gleichung $\text{II}$ kannst $t$ berechnen:

$\begin{array}{} \text{II}\quad&3,5 \cdot t&=&1,5 \quad \mid :3,5\\ & t &=& \dfrac{3}{7} \end{array}$

Setze den Wert $t=\frac{3}{7}$ in die Gleichung $\text{III}$ ein und löse nach $s$ auf:

$\begin{array}{} \text{III}\quad& s&=& 1,3 \end{array}$

Vollständige Lösung anzeigen

Wähle einen der Werte $t$ oder $s$ aus und setze ihn in die entsprechende Geradengleichung ein. Du erhältst so den Schnittpunkt der beiden Geraden, welcher dem Punkt $Q$ entspricht:

$h(1,3)= \pmatrix{3,5 \\ 2,0 \\ 6,3}$

Vollständige Lösung anzeigen

Der Punkt $Q$ muss die Koordinaten $Q(3,5 \mid 2,0 \mid 6,3)$ haben.

2.5

$\blacktriangleright$ Länge der Strebe ermittlen

Mache dir zunächst eine Skizze, welche die Balken $DJ$ , $AG$ und die Strebe zwischen den Balken zeigt. Die grauen Elemente sind Balken und Strebe. Die grünen Elemente sind Hilfslinien. Der Punkt $Y$ liegt auf der $x$ - Achse und hat die gleiche $x$ -Koordinate, wie $G$ .

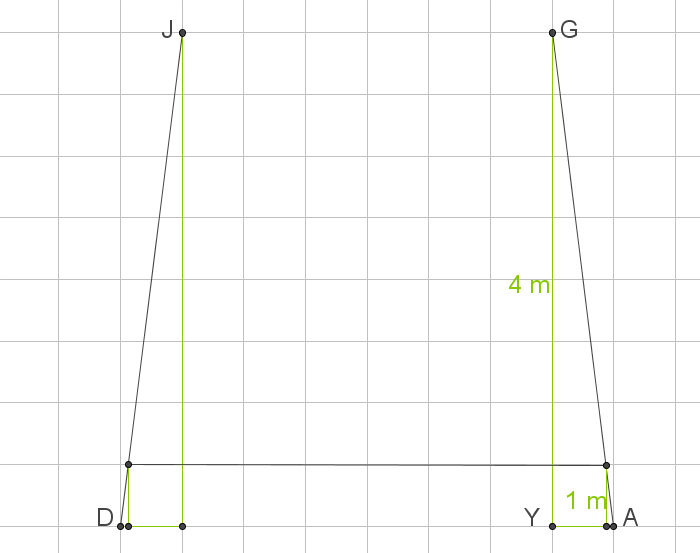Diagramm mit zwei Linien und Maßangaben in Metern auf einem Gitterhintergrund.

Abb. 3: Skizze der Balken mit der Strebe

Die Länge des Querbalkens kannst du berechnen, indem du zuerst die Länge der Strecke $|AD|$ berechnest und anschließend auf jeder Seite die Strecke $x$ abziehst. Da das Bild symmetrisch ist, ist im folgenden nur die rechte Seite, mit mehr Details abgebildet:

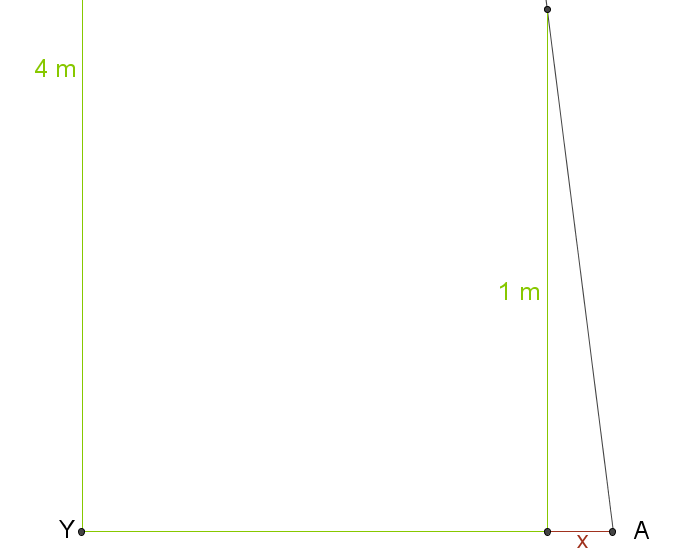Diagramm mit einer vertikalen Linie und Markierungen für 1 m und 4 m.

Abb. 4: Datailansicht der Skizze

Die eingezeichnete Höhe des Balkens ist Parallel zu der Verbindungsstrecke $GY$ . Wählst du den Punkt $A$ als Streckzentrum, kannst du das kleine Dreieck, welches die höhe des Balken enthält, mit dem Streckfaktor $4$ strecken und erhältst das Dreieck $AGY$ . Die länge von $x$ ist demnach ein Viertel der Länge von $AY$ .

$\begin{array}[t]{rll} |AY|&=&\,\bigg \vert \,\pmatrix{3,5 \\ 0 \\ 0}-\pmatrix{4 \\ 0 \\ 0} \\[5pt] &=& \,\bigg \vert \,\pmatrix{0,5 \\ 0 \\ 0}\,\bigg \vert \, \\ &=& 0,5 \end{array}$

Berechne damit die Länge von $x$ :

$\begin{array}[t]{rll} x&=&\frac{1}{4} \cdot 0,5 \\ &=& 0,125 \end{array}$

Jetzt kannst du die Länge des Querbalken, wie oben beschrieben berechnen:

$|AD|-2\cdot x$ $= 4- 2 \cdot 0,125$ $= 3,75 \approx 3,8$

Die Länge des Querbalken beträgt $3,8\text{m}$ .

2.6

$\blacktriangleright$ Befestigung der Streben im rechten Winkel überprüfen

Du sollst überprüfen, ob es einen Punkt $V$ Auf dem Balken $\overline{DJ}$ gibt, den du mit $C$ und $I$ verbinden kannst, sodass zwischen den Vektoren $\overrightarrow{CV}$ und $\overrightarrow{IV}$ ein rechter Winkel entsteht. Um dies zu überprüfen, brauchst du als Erstes die allgemeine Form des Punktes $V$ , auf der Strecke $\overline{DJ}$ . Bestimme dazu die Gleichung der Geraden $j$ durch die Punkte $D$ und $J$ :

$j: \overrightarrow{x}=\pmatrix{0 \\ 0 \\ 0}+t \cdot \pmatrix{0,5 \\ 0,5 \\ 4,0}$

Ein allgemeiner Punkt auf dieser Geraden ist:

$V(0,5t\mid 0,5t \mid 4,0 t)$

Damit kannst du die Verbindungsvektoren $\overrightarrow{CV}$ und $\overrightarrow{IV}$ allgemein bestimmen:

$\overrightarrow{CV}$ $=\pmatrix{0,5 t \\ 0,5t \\ 4,0t}-\pmatrix{0 \\ 3,5 \\ 0}$ $=\pmatrix{0,5t \\ 0,5t-3,5 \\ 4,0t}$

$\overrightarrow{IV}$ $= \pmatrix{0,5 t \\ 0,5t \\ 4,0t}-\pmatrix{0,5 \\ 3,0 \\ 4,0}$ $=\pmatrix{0,5-0,5t \\ 0,5t-3,0 \\ 4,0t-4,0}$

Die beiden Vektoren können nur dann einen rechten Winkel einschließen, wenn es ein $t$ gibt, sodass das Produkt der Vektoren Null ergibt. Bilde also zuerst das Produkt der Vekroten:

$\begin{array}[t]{rll} \overrightarrow{CV} \cdot \overrightarrow{IV}&=& ... \end{array}$

Vollständige Lösung anzeigen

Du erhältst also eine quadratische Funktion. Diese kannst du in deinen Taschenrechner eingeben und auf Nullstellen untersuchen. Du erhältst folgendes Bild:

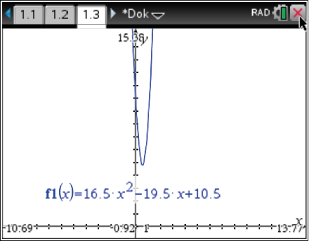Graf einer quadratischen Funktion mit Koordinatenachsen und einer Gleichung.

Abb. 5: Untersuchung auf Nullstellen

Du siehst, dass es in dem ausgewählten Intervall keine Nullstelle gibt. Da es sich um eine quadratische Funktion handelt, welche keine weiteren Extrempunkte hat, kann es auch in keinem anderen Intervall eine Nullstelle geben. Du kannst also kein $t$ finden, für das das Produkt der Vektoren Null ist. Deswegen ist es nicht möglich, die Streben so zu befestigen, dass diese einen rechten Winkel bilden.

2.7

$\blacktriangleright$ Erwartungswert der Länge der Nägel bestimmen

Der Erwartungswert einer normalverteilten Zufallsvariablen entspricht der Extremstelle der Verteilungsfunktion. Die Verteilungsfunktion ist symmetrisch zu der Extremstelle. Du kannst der Aufgabenstellung entnehmen, dass $1\%$ der Nägel kürzer als $85\text{mm}$ und $1\%$ der Nägel länger als $99\text{mm}$ . Diese beiden Werte sind wegen der Symmetrie der Verteillungsfunktion gleich weit von der Extremstelle und damit vom Erwartungswert entfernt.

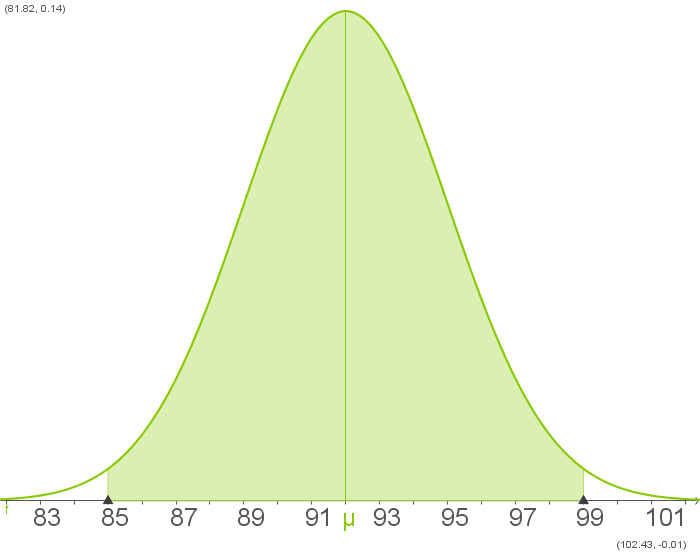Grafik einer Normalverteilungskurve in hellgrün mit Achsen und Mittelwert.

Abb. 6: Normalverteilung

Du kannst den Erwartungswert deswegen berechnen, indem du den Mittelwert der beiden gegebenen Nagellängen bestimmst:

$(85 \text{mm} +99 \text{mm}):2 = 92 \text{mm}$

Der Erwartungswert ist $\mu =92$ .

$\blacktriangleright$ Standardabweichung der Länge der Nägel bestimmen

Du kannst der Aufgabenstellung entnehmen, dass $1\%$ der Werte geringer als $85$ und $1\%$ der Werte größer als $99$ sind. Damit liegen $98\%$ Der Werte im Intervall $[85,99]$ . Formal kannst du das wie folgt ausdrücken:

$P(85 \le X\le 99)=0,98$

Um die Standardabweichung zu bestimmen, verwendest du die Formel für die Intervallwahrscheinlichkeit einer normalverteilten Zufallsgröße.

$P(a \le X\le b)$ $= \Phi(\dfrac{b- \mu}{\sigma})-\Phi(\dfrac{a- \mu}{\sigma})$

Den Erwartungswert $\mu =92$ hast du im Aufgabenteil vorher bereits berechnet, sodass du alle bekannten Werte einsetzten kannst:

$\begin{array}[t]{rll} P(85 \le X\le 99)&=& ... \end{array}$

Vollständige Lösung anzeigen

Du kannst diesen Ausdruck weiter vereinfachen, indem du die folgende Formel verwendest:

$\Phi (-z)=1-\Phi(z)$

$\begin{array}[t]{rll} \Phi\Bigg(\dfrac{7}{\sigma}\Bigg)-\Phi\Bigg(\dfrac{-7}{\sigma}\Bigg)&=& ... \end{array}$

Vollständige Lösung anzeigen

Insgesamt hast du also folgende Gleichung:

$2\cdot \Phi\Bigg(\dfrac{7}{\sigma}\Bigg) -1 = 0,99$

Vollständige Lösung anzeigen

Jetzt musst du in der Tabelle der Standardnormalverteilung, welche du gegeben hast, ablesen, für welchen Wert $z$ gilt:

$\Phi(z)= 0,99$

Du kannst ablesen, dass diese Gleichung für den Wert $z=2,34$ erfüllt ist. Da $z$ dem Bruch $\dfrac{7}{\sigma}$ entspricht, kannst du die Standardabweichung $\sigma$ jetzt durch Umformung berechnen:

$\begin{array}[t]{rll} \dfrac{7}{\sigma}&=& 2,34 &\quad \scriptsize \mid\; \cdot \sigma : 2,34 \\[5pt] \sigma&\approx& 3 \end{array}$

Die Standardabweichung ist $\sigma=3$ .

2.8

$\blacktriangleright$ Wahrscheinlichkeit berechnen

Das Kind zieht zuerst aus Gefäß $A$ . Die Wahrscheinlichkeit dafür, dass das Los ein Reh bzw. ein Kuckuck zeigt ist:

$P(R_A)=\frac{3}{7}$

$P(K_A)=\frac{4}{7}$

Da die Wahrscheinlichkeiten für den zweiten Zug vom Ersten abhängen, musst du für den zweiten Zug bedingte Wahrscheinlichkeiten berechnen. Zieht das Kind im ersten Zug ein Reh, sind $2$ Rehe und $2$ Kuckucke in Gefäß $B$ . Die Wahrscheinlichkeit dafür, dass das Kind im zweiten Zug einen Kuckuck zieht ist deswegen

$P(K_B \mid R_A)=\frac{2}{4}$

Zieht das Kind im ersten Zug einen Kuckuck, sind $1$ Reh und $3$ Kuckucke im Gefäß $B$ . Die Wahrscheinlichkeit dafür, dass das Kind im zweiten Zug einen Kuckuck zieht ist deswegen

$P(K_B \mid K_A)=\frac{3}{4}$

Die Wahrscheinlichkeit, dass das Kind im zweiten Zug einen Kuckuck zieht und diesen in Gefäß $C$ legt, setzt sich jetzt wie folgt zusammen:

$...$

Vollständige Rechnung anzeigen

Die Wahrscheinlichkeit dafür, dass das Kind gewinnt, beträgt $64,3 \%$

Bildnachweise [nach oben]

[1]

[2]

[3]

[4]

[5]

[6]

Aufgabe B2

2.1

$\blacktriangleright$ Koordinaten von $\boldsymbol{O}$ bestimmen

$\begin{array}[t]{rll} \overrightarrow{OO}&=&\overrightarrow{OL}+\overrightarrow{GJ} &\quad \\[5pt] \end{array}$

Der Ortsvektor $\overrightarrow{OL}$ entspricht in seinen Koordinaten dem Punkt $L$ . Den Vektor $\overrightarrow{GJ}$ erhältst du wie folgt:

Damit kannst du den Ortsvektor zu $O$ bestimmen:

Der Punkt $O$ hat also die Koordinaten $O(0,5\mid 2,0\mid 5,0)$ .

2.2

$\blacktriangleright$ Neigungswinkel bestimmen

$E: z=0$

Wähle jetzt einen Balken, bei dem beide Endpunkte angegeben sind und bestimme den Verbindungsvektor. Du kannst zum Beispiel den Balken $AG$ auswählen.

Den Schnittwinkel $\alpha$ zwischen der Ebene $E:z=0$ und dem Vektor $\overrightarrow{u}:=\overrightarrow{AG}$ kannst du mit der Sinus-Formel berechnen:

$\sin\alpha= \dfrac{\left|\vec{n}\cdot\vec{u}\right|}{\left|\vec{n}\right|\cdot\left|\vec{u}\right|}$

Bei dem Vektor $\vec{n}$ handelt es sich um einen Normalenvektor der Ebene $E$ .

Da die Ebene in Koordinatenform angegeben ist, kannst du den Normalenvektor direkt ablesen:

$\overrightarrow{n}=\pmatrix{0 \\ 0 \\ 1}$

Setzte im nächsten Schritt die Vektoren in die Formel ein:

$\begin{array}[t]{rll} \sin\alpha&=& \dfrac{4,0}{4,062}\\ &\approx & 0,9847 \end{array}$

Vollständige Lösung anzeigen

Den Winkel $\alpha$ kannst du jetzt mit deinem Taschenrechner bestimmen:

$\alpha=79,964$

Vollständige Lösung anzeigen

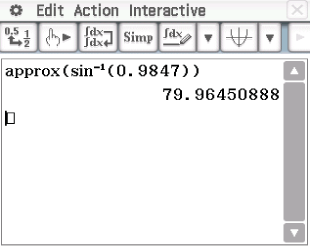Mathematische Berechnung mit einem Ergebnis von 79.96450888 für den Ausdruck approx(sin⁻¹(0.9847)).

Abb. 1: Winkel berechnen mit dem Taschenrechner

Achte darauf, dass dein Taschenrechner auf Degree eingestellt ist.

Der Neigungswinkel zwischen dem Boden und einem Balken des Kanzelblocks beträgt also $79,964° \approx 80°$ .

2.3

$\blacktriangleright$ Abstand zwischen $\boldsymbol{E}$ und $\boldsymbol{A}$ ermitteln

Um den Abstand der beiden Punkte zu berechnen, musst du zuerst die Koordinaten des Punktes $E$ berechnen. Dafür erstellst du dir ein Hilfsdreieck $EZG$ .

Abb. 2: Hilfsdreieck

Die Länge der Strecke $x$ kannst du im nächsten Schritt mit dem Tangens bestimmen:

$\begin{array}[t]{rll} \tan(76°)&\approx& 0,997 \end{array}$

Vollständige Lösung anzeigen

$x-0,5 \approx 0,5$

Vollständige Lösung anzeigen

$E(3,5\mid -0,5 \mid 0)$

Jetzt kannst du den Abstand zwischen den Punkten $A$ und $E$ berechnen:

$|AE|=\,\bigg \vert \, \pmatrix{4 \\ 0 \\0} - \pmatrix{3,5 \\ -0,5 \\ 0} \,\bigg \vert \,$ $=\,\bigg \vert \,\pmatrix{0,5 \\ 0,5 \\ 0,5}\,\bigg \vert \,$ $=\sqrt{0,5} \approx 0,7$

Der Abstand des Punktes $E$ vom Punkt $A$ beträgt somit $0,7\text{m}$ .

2.4

$\blacktriangleright$ Koordinaten von $\boldsymbol{Q}$ überprüfen

Du sollst begründen, dass der Punkt $Q$ die Koordinaten $Q(3,5 \mid 2,0 \mid 6,3)$ haben muss. Gehe dazu wie folgt vor:

Bestimme die Koordinaten von $R$ mithilfe der Koordinaten von $P$ und $S$ .
Bestimme die Gleichung der Geraden $g$ , die durch die Punkte $P$ und $R$ verläuft.
Da die Kanzel ein gerades Prisma ist, ist die Kante $LQ$ parallel zu $GP$ und damit senkrecht zur $xy$ -Ebene. Bestimme die Gleichung der Geraden $h$ , die durch $L$ verläuft und senkrecht zur $xy$ -Ebene ist. Diese Gerade verläuft durch $Q$ .
Bestimme den Schnittpunkt von $g$ und $h$ . Dieser Schnittpunkt entspricht dem Punkt $Q$ .

Schritt 1: Koordinaten von $\boldsymbol{R}$ bestimmen

Der Punkt $R$ hat die gleiche $x$ -Koordinate, wie $P$ und stimmt mit $S$ in seiner $y$ - und $z$ -Koordinaten überein. Deswegen hat $R$ die Koordinaten:

$R(3,5 \mid 4,0 \mid 6,7)$

Schritt 2: Gleichung von $g$ bestimmen

Wähle als Stützvektor der Geraden einen der Punkte $P$ oder $R$ und als Spannvektor den Verbindungsvektor $\overrightarrow{PR}$ :

$\overrightarrow{PR}=\pmatrix{3,5 \\ 4,0 \\ 6,7}-\pmatrix{3,5 \\ 0,5 \\ 6,0} =\pmatrix{0 \\ 3,5 \\ 0,7}$

Mit den Koordinaten des Punktes $P$ , als Stützvektor erhältst du:

$g: \overrightarrow{x}= \pmatrix{3,5 \\ 0,5 \\ 6,0}+t\cdot \pmatrix{0 \\ 3,5 \\ 0,7}$

Schritt 3: Gleichung von $h$ bestimmen

Der Stützvektor der Geraden $h$ ist der Ortsvektor zum Punkt $L$ . Der Spannvektor von $h$ entspricht dem Normalenvektor der $xy$ -Ebene und somit

$\overrightarrow{n}=\pmatrix{0 \\0 \\ 1}$

Mit diesen beiden Vektoren kannst du die Geradengleichung aufstellen:

$h: \overrightarrow{x}= \pmatrix{3,5 \\ 2,0 \\ 5,0}+ s \cdot \pmatrix{0 \\ 0 \\ 1}$

Schritt 4: Koordinaten von $\boldsymbol{Q}$ bestimmen

Durch Gleichsetzten der beiden Geradengleichungen erhältst du ein Lineares Gleichungssystem mit drei Gleichungen und zwei Unbekannten:

$\begin{array}{} \text{I}\quad& ...\\ \text{II}\quad& ... \text{III}\quad& ... \end{array}$

Vollständige Lösung anzeigen

Vereinfache die drei Gleichungen zuerst:

$\begin{array}{} \text{I}\quad&3,5&=&3,5\quad \scriptsize\\ \text{II}\quad&3,5 \cdot t&=&1,5 \quad\\ \text{III}\quad&0,7 \cdot t -s&=&-1,0\quad\\ \end{array}$

Gleichung $\text{I}$ liefert dir keine Aussage. Mit Gleichung $\text{II}$ kannst $t$ berechnen:

$\begin{array}{} \text{II}\quad&3,5 \cdot t&=&1,5 \quad \mid :3,5\\ & t &=& \dfrac{3}{7} \end{array}$

Setze den Wert $t=\frac{3}{7}$ in die Gleichung $\text{III}$ ein und löse nach $s$ auf:

$\begin{array}{} \text{III}\quad & s&=& 1,3 \end{array}$

Vollständige Lösung anzeigen

Wähle einen der Werte $t$ oder $s$ aus und setze ihn in die entsprechende Geradengleichung ein. Du erhältst so den Schnittpunkt der beiden Geraden, welcher dem Punkt $Q$ entspricht:

$h(1,3)= \pmatrix{3,5 \\ 2,0 \\ 6,3}$

Vollständige Lösung anzeigen

Der Punkt $Q$ muss die Koordinaten $Q(3,5 \mid 2,0 \mid 6,3)$ haben.

2.5

$\blacktriangleright$ Länge der Strebe ermittlen

Abb. 3: Skizze der Balken mit der Strebe

Abb. 4: Datailansicht der Skizze

$\begin{array}[t]{rll} |AY|&=&\,\bigg \vert \,\pmatrix{3,5 \\ 0 \\ 0}-\pmatrix{4 \\ 0 \\ 0} \\[5pt] &=& \,\bigg \vert \,\pmatrix{0,5 \\ 0 \\ 0}\,\bigg \vert \, \\ &=& 0,5 \end{array}$

Berechne damit die Länge von $x$ :

$\begin{array}[t]{rll} x&=&\frac{1}{4} \cdot 0,5 \\ &=& 0,125 \end{array}$

Jetzt kannst du die Länge des Querbalken, wie oben beschrieben berechnen:

$|AD|-2\cdot x$ $= 4- 2 \cdot 0,125$ $= 3,75 \approx 3,8$

Die Länge des Querbalken beträgt $3,8\text{m}$ .

2.6

$\blacktriangleright$ Befestigung der Streben im rechten Winkel überprüfen

$j: \overrightarrow{x}=\pmatrix{0 \\ 0 \\ 0}+t \cdot \pmatrix{0,5 \\ 0,5 \\ 4,0}$

Ein allgemeiner Punkt auf dieser Geraden ist:

$V(0,5t\mid 0,5t \mid 4,0 t)$

Damit kannst du die Verbindungsvektoren $\overrightarrow{CV}$ und $\overrightarrow{IV}$ allgemein bestimmen:

$\overrightarrow{CV}$ $= \pmatrix{0,5 t \\ 0,5t \\ 4,0t}-\pmatrix{0 \\ 3,5 \\ 0}$ $=\pmatrix{0,5t \\ 0,5t-3,5 \\ 4,0t}$

$\overrightarrow{IV}$ $= \pmatrix{0,5 t \\ 0,5t \\ 4,0t}-\pmatrix{0,5 \\ 3,0 \\ 4,0}$ $=\pmatrix{0,5-0,5t \\ 0,5t-3,0 \\ 4,0t-4,0}$

Die beiden Vektoren können nur dann einen rechten Winkel einschließen, wenn es ein $t$ gibt, sodass das Produkt der Vektoren Null ergibt. Bilde also zuerst das Produkt der Vekroten:

$\begin{array}[t]{rll} \overrightarrow{CV} \cdot \overrightarrow{IV}&=& ... \end{array}$

Vollständige Lösung anzeigen

Du erhältst also eine quadratische Funktion. Diese kannst du in deinen Taschenrechner eingeben und auf Nullstellen untersuchen. Du erhältst folgendes Bild:

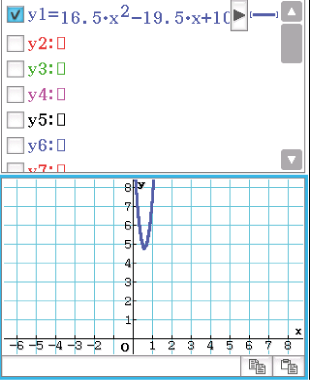Grafik eines Koordinatensystems mit einer Parabel und mehreren Funktionen im Plot-Tool.

Abb. 5: Untersuchung auf Nullstellen

2.7

$\blacktriangleright$ Erwartungswert der Länge der Nägel bestimmen

Abb. 6: Normalverteilung

Du kannst den Erwartungswert deswegen berechnen, indem du den Mittelwert der beiden gegebenen Nagellängen bestimmst:

$(85 \text{mm} +99 \text{mm}):2 = 92 \text{mm}$

Der Erwartungswert ist $\mu =92$ .

$\blacktriangleright$ Standardabweichung der Länge der Nägel bestimmen

$P(85 \le X\le 99)=0,98$

Um die Standardabweichung zu bestimmen, verwendest du die Formel für die Intervallwahrscheinlichkeit einer normalverteilten Zufallsgröße.

$P(a \le X\le b)$ $= \Phi(\dfrac{b- \mu}{\sigma})-\Phi(\dfrac{a- \mu}{\sigma})$

Den Erwartungswert $\mu =92$ hast du im Aufgabenteil vorher bereits berechnet, sodass du alle bekannten Werte einsetzten kannst:

$\begin{array}[t]{rll} P(85 \le X\le 99)&=& ... \end{array}$

Vollständige Lösung anzeigen

Du kannst diesen Ausdruck weiter vereinfachen, indem du die folgende Formel verwendest:

$\Phi (-z)=1-\Phi(z)$

$\begin{array}[t]{rll} \Phi\Bigg(\dfrac{7}{\sigma}\Bigg)-\Phi\Bigg(\dfrac{-7}{\sigma}\Bigg)&=& ... \end{array}$

Vollständige Lösung anzeigen

Insgesamt hast du also folgende Gleichung:

$\begin{array}[t]{rll} \Phi\Bigg(\dfrac{7}{\sigma}\Bigg)&=& 0,99 \\ \end{array}$

Vollständige Lösung anzeigen

Jetzt musst du in der Tabelle der Standardnormalverteilung, welche du gegeben hast, ablesen, für welchen Wert $z$ gilt:

$\Phi(z)= 0,99$

$\begin{array}[t]{rll} \dfrac{7}{\sigma}&=& 2,34 &\quad \scriptsize \mid\; \cdot \sigma : 2,34 \\[5pt] \sigma&\approx& 3 \end{array}$

Die Standardabweichung ist $\sigma=3$ .

2.8

$\blacktriangleright$ Wahrscheinlichkeit berechnen

Das Kind zieht zuerst aus Gefäß $A$ . Die Wahrscheinlichkeit dafür, dass das Los ein Reh bzw. ein Kuckuck zeigt ist:

$P(R_A)=\frac{3}{7}$

$P(K_A)=\frac{4}{7}$

$P(K_B \mid R_A)=\frac{2}{4}$

Zieht das Kind im ersten Zug einen Kuckuck, sind $1$ Reh und $3$ Kuckucke im Gefäß $B$ . Die Wahrscheinlichkeit dafür, dass das Kind im zweiten Zug einen Kuckuck zieht ist deswegen

$P(K_B \mid K_A)=\frac{3}{4}$

Die Wahrscheinlichkeit, dass das Kind im zweiten Zug einen Kuckuck zieht und diesen in Gefäß $C$ legt, setzt sich jetzt wie folgt zusammen:

$...$

Vollständige Rechnung anzeigen

Die Wahrscheinlichkeit dafür, dass das Kind gewinnt, beträgt $64,3 \%$

Bildnachweise [nach oben]

[1]

[2]

[3]

[4]

[5]

[6]