Wahlbereich

Gegeben ist die Funktion $f$ mit $f(x)=\frac{1}{x} \quad(x \in \mathbb{R}, x\gt0).$ Betrachtet wird die Tangente an den Graphen von $f$ im Punkt $\left(a \,\big\vert\, \frac{1}{a}\right) \quad(a \in \mathbb{R}, a\gt0).$

5.1

Zeige, dass die Tangente den Anstieg $-\frac{1}{a^2}$ hat.

(1 BE)

5.2

Die Tangente schließt mit den beiden Koordinatenachsen im ersten Quadranten ein Dreieck ein.
Begründe, dass der Flächeninhalt dieses Dreiecks unabhängig von $a$ ist.

(4 BE)

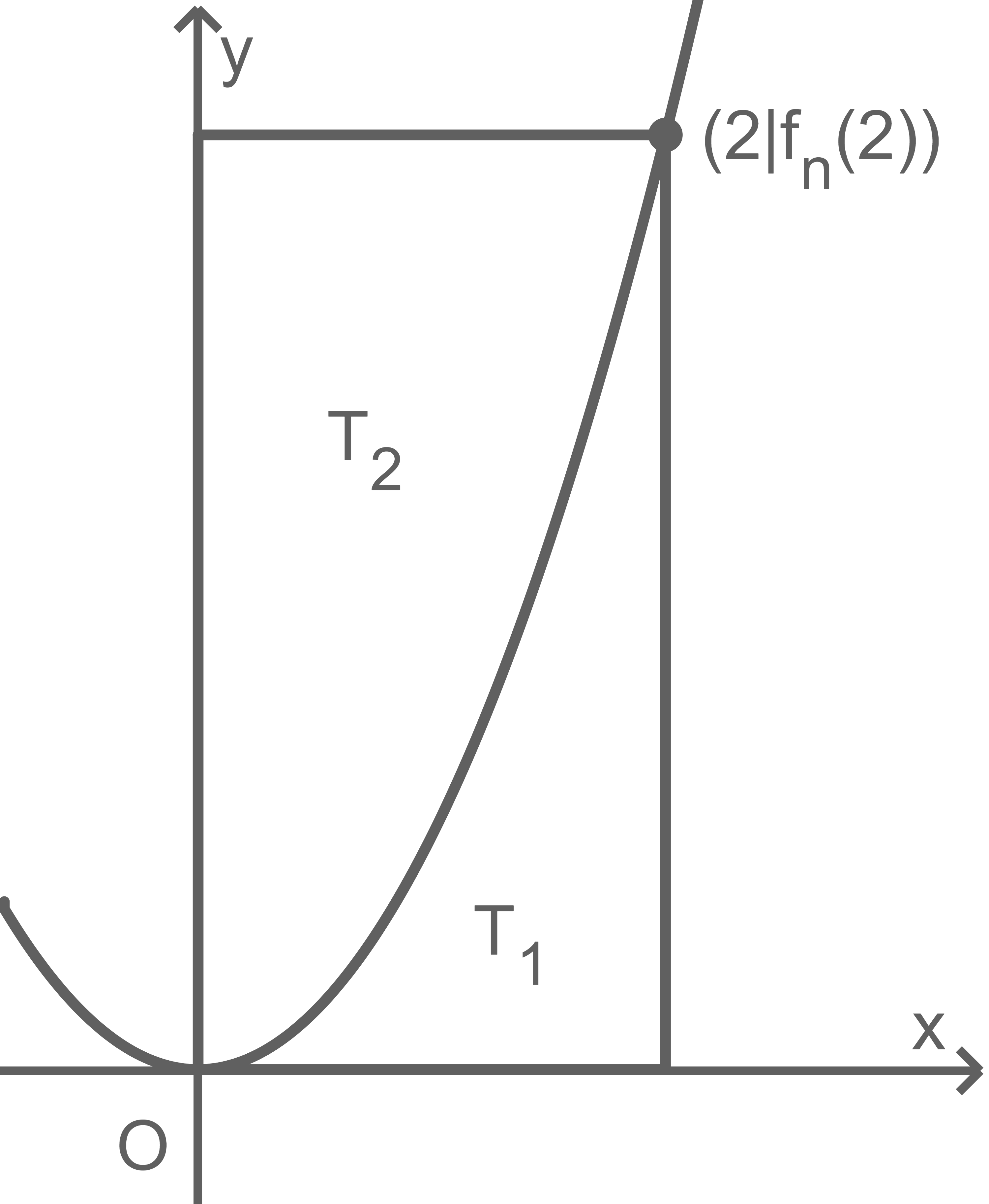
Für jede natürliche Zahl $n$ mit $n\gt1$ sind der Graph der in $\mathbb{R}$ definierten Funktion $f_n$ mit $f_n(x)=x^n$ und ein Rechteck mit einem Eckpunkt $(2\mid f_n(2))$ gegeben. Zwei Seiten des Rechtecks liegen auf den Koordinatenachsen. Für jedes $n$ zerlegt der Graph von $f_n$ das zugehörige Rechteck in die Teilflächen $T_1$ und $T_2.$ Die Abbildung zeigt den Sachverhalt für einen Wert von $n.$ Bestimme den Anteil des Flächeninhalts von $T_1$ am Flächeninhalt des Rechtecks.

(5 BE)

Die Punkte $A(1\mid1\mid 0), B(4\mid3\mid 0)$ und $C(-2\mid3\mid 0)$ sind die Eckpunkte der Grundfläche einer Pyramide, deren Spitze $S$ auf der Geraden $g: \overrightarrow{x}=\pmatrix{4\\-3\\5}+r \cdot\pmatrix{-1\\2\\0} \quad(r \in \mathbb{R})$ liegt.

7.1

Begründe, dass $g$ parallel zur Grundfläche verläuft.

(1 BE)

7.2

Die Gerade $h$ verläuft durch $S$ und senkrecht zur Grundfläche der Pyramide. Sie schneidet die Kante $\overline{B C}.$
Ermittle für diesen Fall die Koordinaten von $S.$

(4 BE)

Gegeben sind die Punkte $A(1\mid1\mid-1), B_t(1\mid1+t\mid-1+2 \cdot t)$ und $C_t(1+2 \cdot t\mid1-t\mid-1)$ für positive reelle Zahlen $t.$

8.1

Prüfe, ob die Vektoren $\overrightarrow{A B_2}$ und $\overrightarrow{A C_4}$ linear unabhängig sind.

(2 BE)

8.2

Zeige, dass die Punkte $A, B_t$ und $C_t$ für jedes $t$ ein und dieselbe Ebene bestimmen.

(3 BE)

Ein Glücksrad hat drei Sektoren, einen roten, einen gelben und einen blauen. Es gelten folgende Bedingungen:

Bei jeder Drehung wird der rote und der gelbe Sektor jeweils mit der gleichen Wahrscheinlichkeit erzielt.
Die Wahrscheinlichkeit für das Ereignis „Beim dreimaligen Drehen wird genau einmal der blaue Sektor erzielt." ist möglichst groß.

Bestimme für jeden Sektor die Wahrscheinlichkeit, mit der dieser bei einer Drehung erzielt wird.

(5 BE)

Für die beiden Ereignisse $A$ und $B$ gilt: $P(A)=\frac{1}{3}$ und $P(B)=\frac{1}{4}.$ Die Wahrscheinlichkeit für das gleichzeitige Eintreten der beiden Ereignisse sei $p.$

10.1

Begründe, dass gilt: $p \leq \frac{1}{4}.$

(2 BE)

10.2

Bestimme die Wahrscheinlichkeit $P_{\overline{A}}\left(\overline{B}\right)$ in Abhängigkeit von $p.$

(3 BE)

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?

5.1

Für die Ableitung von $f$ gilt:

$\(f$

Somit folgt für den Anstieg $m$ der Tangente:

$\(\begin{array}[t]{rlll} m&=&f$

5.2

Einsetzen des Punktes $\left(a\mid\frac{1}{a}\right)$ in die Tangentengleichung $y=-\dfrac{1}{a^2}x+b$ liefert:

$\begin{array}[t]{rlll} \frac{1}{a}&=&-\dfrac{1}{a^2}\cdot a+b &\mid\;+\dfrac{1}{a} \\[5pt] \frac{2}{a}&=&b \end{array}$

Die vollständige Tangentengleichung ergibt sich somit als $y=-\dfrac{1}{a^2}x+\frac{2}{a}.$

Die Strecken vom Koordinatenursprung zu den jeweiligen Achsenschnittpunkten der Tangente liefern die Längen der Katheten des Dreiecks.

Die eine Kathete ist somit durch den $y$ -Achsenabschnitt $\frac{2}{a}$ gegeben. Für die andere Kathetenlänge folgt:

$\begin{array}[t]{rlll} -\dfrac{1}{a^2}x+\frac{2}{a}&=&0 &\mid\;-\frac{2}{a} \\[5pt] -\dfrac{1}{a^2}x&=&-\frac{2}{a} &\mid\;:\left(-\frac{1}{a^2}\right) \\[5pt] x&=&2a \end{array}$

Insgesamt ergibt sich somit der Flächeninhalt des Dreiecks wie folgt:

$A=\dfrac{1}{2}\cdot\frac{2}{a}\cdot2a=2\;[\text{LE}].$

1. Schritt: Flächeninhalt $\boldsymbol{T_1}$ berechnen

Der rechte untere Eckpunkt des Rechtecks besitzt aufgrund der Achsenparallelität des Rechtecks die Koordinaten $(2\mid 0).$

Für den Flächeninhalt $T_1$ gilt also:

$\begin{array}[t]{rll} T_1&=& \displaystyle\int_{0}^{2}f_n(x)\;\mathrm dx&\\[5pt] &=& \displaystyle\int_{0}^{2}x^n\;\mathrm dx&\\[5pt] &=& \left[\dfrac{1}{n+1}x^{n+1}\right]_0^2&\\[5pt] &=& \dfrac{1}{n+1}\cdot 2^{n+1}-\dfrac{1}{n+1}\cdot 0^{n+1} &\\[5pt] &=& \dfrac{1}{n+1}\cdot 2^{n+1} \;[\text{FE}] \end{array}$

2. Schritt: Flächeninhalt $\boldsymbol{A_R}$ des Rechtecks berechnen

Das Rechteck besitzt die Breite $2$ und die Höhe $f_n(2).$ Diese ergibt sich mit:

$f_n(2)=2^n\;\text{LE}$

Das Rechteck besitzt somit den Flächeninhalt $A_{R}=2\cdot 2^n=2^{n+1} \;[\text{FE}].$

3. Schritt: Anteil bestimmen

$\begin{array}[t]{rll} \dfrac{T_1}{A_R}&=& \dfrac{\frac{1}{n+1}\cdot 2^{n+1}}{2^{n+1}} & \\[5pt] &=& \dfrac{1}{n+1} \end{array}$

7.1

Die Grundfläche liegt in der von den drei angegebenen Punkten aufgespannten Ebene. Da alle drei Punkte die $z$ -Koordinate $0$ besitzen, ist das die $x$ - $y$ -Ebene. Der Richtungsvektor der angegebenen Gerade besitzt zudem die $z$ -Koordinate $0.$ Somit verläuft die Gerade parallel zur Grundfläche.

7.2

Die beiden Punkte $B$ und $C$ liegen zusätzlich zur $x$ - $y$ -Ebene auch in der Ebene $y=3.$ Da somit die Strecke $\overline{BC}$ vollständig in dieser Ebene liegt, besitzt der Punkt $S$ die $y$ -Koordinate $3.$ Aus der zweiten Zeile der Geradengleichung folgt:

$\begin{array}[t]{rlll} -3+2r&=&3 &\mid\;+3 \\[5pt] 2r&=&6 &\mid\;:2 \\[5pt] r&=&3 \end{array}$

Einsetzen in die Geradengleichung liefert:

$\begin{array}[t]{rlll} \overrightarrow{OS}&=&\pmatrix{4\\-3\\5}+3\cdot\pmatrix{-1\\2\\0} &\mid\; \\[5pt] &=&\pmatrix{1\\3\\5} \end{array}$

Die Koordinaten der Pyramidenspitze ergeben sich somit als $S(1\mid3\mid5).$

8.1

Für die beiden betrachteten Vektoren gilt:

$\begin{array}[t]{rlll} \overrightarrow{AB_2}&=&\pmatrix{1\\3\\3}-\pmatrix{1\\1\\-1} &\mid\; \\[5pt] &=&\pmatrix{0\\2\\4} \end{array}$

$\begin{array}[t]{rlll} \overrightarrow{AC_4}&=&\pmatrix{9\\-3\\-1}-\pmatrix{1\\1\\-1} &\mid\; \\[5pt] &=&\pmatrix{8\\-4\\0} \end{array}$

$\lambda\cdot\pmatrix{0\\2\\4}+\mu\cdot\pmatrix{8\\-4\\0}$

8.2

$\begin{array}[t]{rlll} \overrightarrow{AB_t}&=&\pmatrix{1\\1+t\\-1+2t}-\pmatrix{1\\1\\-1} &\mid\; \\[5pt] &=&\pmatrix{0\\t\\2t} \end{array}$

$\begin{array}[t]{rlll} \overrightarrow{AC_t}&=&\pmatrix{1+2t\\1-t\\-1}-\pmatrix{1\\1\\-1} &\mid\; \\[5pt] &=&\pmatrix{2t\\-t\\0} \end{array}$

Für den Normalenvektor der Ebene folgt mit dem Kreuzprodukt:

$\begin{array}[t]{rlll} \overrightarrow{AB_t}\times\overrightarrow{AC_t}&=&\pmatrix{0\\t\\2t}\times\pmatrix{2t\\-t\\0} \\[5pt] &=&\pmatrix{0-(-t)\cdot2t\\2t\cdot2t-0\\0-2t\cdot t} \\[5pt] &=&\pmatrix{2t^2\\4t^2\\-2t^2} \end{array}$

Skalieren des Normalenvektors mit $\frac{1}{2t^2}$ ergibt den alternativen Vektor:

$\pmatrix{1\\2\\-1}$

Damit folgt $E:x+2y-z=d.$ Da die Koordinaten von $A$ unabhängig von $t$ sind, liefert einsetzen dieser in die Ebenengleichung einen Wert für $d,$ der ebenfalls unabhängig von $t$ ist. Somit bestimmen die drei Punkte für jeden Wert von $t$ die gleiche Ebene.

Die Wahrscheinlichkeit den roten Sektor zu erzielen, wird mit $p$ bezeichnet. Für den gelben Sektor ergibt sich nach der ersten Bedingung ebenfalls $p$ und somit für den blauen $1-2p.$
Für die Wahrscheinlichkeit, bei dreimaligem Drehen genau einmal den blauen Sektor zu erzielen, ergibt sich in Abhängigkeit von $p:$

$\begin{array}[t]{rlll} f(p)&=&3\cdot(2p)^2\cdot(1-2p) \\[5pt] &=&-24p^3+12p^2 \end{array}$

Für die Ableitung von $f$ gilt:

$\(f$

Nullsetzen der Ableitung liefert die möglichen Extremstellen:

$\(\begin{array}[t]{rlll} f$

Mit dem Satz des Nullprodukts folgt $p=0$ als eine Nullstelle. Für die andere gilt:

$\begin{array}[t]{rlll} &-3p+1=&0 &\mid\;-1 \\[5pt] &-3p=&-1 &\mid\;:(-3) \\[5pt] p&=&\frac{1}{3} \end{array}$

Da $p$ eine Wahrscheinlichkeit ist und somit $0\lt p\lt1$ gelten muss, kommt nur $p=\frac{1}{3}$ infrage. Da $f(0)=0$ und $f(1)\lt0$ gilt, muss $f$ an der Stelle $p=\frac{1}{3}$ einen Hochpunkt besitzen.

Somit gilt $p=\frac{1}{3}$ und da $1-2\cdot\frac{1}{3}=\frac{1}{3}$ ist, beträgt die Wahrscheinlichkeit bei einer Drehung erzielt zu werden für alle drei Sektoren jeweils $\frac{1}{3}.$

10.1

Da Wahrscheinlichkeiten nicht negativ sein können, gelten die folgenden Ungeichungen:

$P\left(\overline{A}\cap B\right)=\dfrac{1}{4}-p\geq0$

$P\left(A\cap \overline{B}\right)=\dfrac{1}{3}-p\geq0$

Durch Umstellen folgt $p\leq\frac{1}{3}$ sowie $p\leq\frac{1}{4}$ und damit insbesondere letzteres.

10.2

Mit der Gegenwahrscheinlichkeit folgt für $P\left(\overline{A}\cap\overline{B}\right):$

Rechenweg anzeigen

$P\left(\overline{A}\cap\overline{B}\right) = \dfrac{5}{12}+p$

Damit folgt für die gesuchte Wahrscheinlichkeit:

$P_{\overline{A}}\left(\overline{B}\right)=\dfrac{P\left(\overline{A}\cap\overline{B}\right)}{P\left(\overline{A}\right)}=\dfrac{\frac{5}{12}+p}{\frac{2}{3}}$

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?