Teil B1

Eine Glocke besitzt die Form eines Rotationskörpers und besteht aus der Glockenhaube und dem Glockenkörper.
In die Querschnittsfläche dieser Glocke wird ein kartesisches Koordinatensystem mit dem Koordinatenursprung $O$ $(1$ Längeneinheit entspricht $10\,\text{cm})$ gelegt (siehe Abbildung).
Die Abszissenachse ist die Symmetrieachse der Querschnittsfläche der Glocke und beschreibt die Symmetrieachse der Glocke.
Ein Teil der Querschnittsfläche der Glockenhaube wird durch die Graphen der Funktionen $f$ und $g$ begrenzt.
Ein Teil der Querschnittsfläche des Glockenkörpers wird durch die Graphen der Funktionen $h,$ $j$ und $k$ begrenzt.

Abb. 1: nicht maßstäblich

Dabei gilt:

$f(x)=$ $2,0\cdot x +2,60\quad$ $\left(x\in \mathbb{R}; -\frac{13}{10}\leq x\leq 0,00\right)$

$g(x)=$ $2,8\cdot x +2,20\quad$ $\left(x\in \mathbb{R}; -\frac{11}{14}\leq x\leq 0,00\right)$

$h(x)=$ $0,05\cdot x^2-0,05\cdot x +2,60\quad$ $\left(x\in \mathbb{R}; 0,00\leq x\leq 7,11\right)$

$j(x)=$ $0,05\cdot x^2-0,07\cdot x +2,20\quad$ $\left(x\in \mathbb{R}; 0,00\leq x\leq 7,90\right)$

$k(x)=$ $4,77 \quad$ $\left(x\in \mathbb{R}; 7,11\leq x\leq 7,90\right)$

1.1

Im Punkt $P(0,00\mid g(0,00))$ gehen zwei Begrenzungslinien der Querschnittsfläche der Glocke ineinander über und schließen einen stumpfen Winkel $\alpha$ ein.
Zeige, dass $P$ auf dem Graphen von $j$ liegt.
Berechne die Größe von $\alpha.$

Erreichbare BE-Anzahl: 6

1.2

Die Materialdicke der Glockenhaube entspricht der Dicke der Querschnittsfläche der Glockenhaube. Die Dicke der Querschnittsfläche der Glockenhaube wird jeweils ausgehend von einem Punkt des Graphen von $g$ und senkrecht zum Graphen von $f$ gemessen.
Weise nach, dass die Glockenhaube ausgehend vom Punkt $Q(-0,50\mid g(-0,50))$ eine Materialdicke von $3,6\,\text{cm}$ besitzt.

Erreichbare BE-Anzahl: 6

1.3

Ermittle den Flächeninhalt der Querschnittsfläche der Glocke in Quadratdezimetern.

Erreichbare BE-Anzahl: 5

1.4

Die Glocke besteht aus einem Material mit der Dichte $\rho = 8,5\,\dfrac{\text{g}}{\text{cm}^3}.$
Berechne die Gesamtmasse von Glockenkörper und Glockenhaube in Kilogramm.

Erreichbare BE-Anzahl: 7

1.5

Es gilt:
Wenn eine Funktion $p$ im Intervall $a\leq x\leq b$ mit $a,b\in \mathbb{R}$ stetig ist, dann lässt sich der Mittelwert aller Funktionswerte von $p$ in diesem Intervall mit dem Term $\dfrac{1}{b-a}\cdot \displaystyle\int_{a}^{b}p(x)\;\mathrm dx$ berechnen.
An jeder Stelle $x$ $(x\in \mathbb{R}; 0,00\leq x\leq 7,90)$ besitzt der Glockenkörper einen Innendurchmesser.
Zeige, dass der Mittelwert aller Innendurchmesser des Glockenkörpers nicht mit dem Innendurchmesser des Glockenkörpers an der Stelle $x=3,95$ übereinstimmt.
Untersuche, ob der Mittelwert aller Innendurchmesser des Glockenkörpers mit dem arithmetischen Mittel des kleinsten und größten Innendurchmessers des Glockenkörpers übereinstimmt.

Erreichbare BE-Anzahl: 8

1.6

Beim Läuten schlägt ein Klöppel in einem Anschlagpunkt am Glockenkörper an (siehe Abbildung). Der geradelinige Klöppel ist $100,0\,\text{cm}$ lang und ist mit einem seiner Endpunkte im Punkt $O$ beweglich gelagert. Zur vereinfachten Berechnung wird die Dicke des Klöppels vernachlässigt.
Berechne, in welchem Verhältnis der Anschlagpunkt die Länge des Klöppels teilt.

Erreichbare BE-Anzahl: 6

1.7

Eine Gießerei weiß, dass nach dem Gießen genau $10\,\%$ der Glocken einen optischen Fehler und genau $20\,\%$ der Glocken einen Klangfehler besitzen.
Die Gießerei ist der Auffassung, dass damit nach dem Gießen genau $70\,\%$ aller Glocken keinen optischen Fehler und keinen Klangfehler besitzen.
Gib an, unter welcher Bedingung die Auffassung der Gießerei falsch ist.
Begründe deine Angabe.

Erreichbare BE-Anzahl: 3

1.8

Für die Aufhängung der Klöppel werden Bolzen verwendet. Die Länge dieser Bolzen ist normalverteilt mit dem Erwartungswert $\mu = 10,0\,\text{cm}$ und der Standardabweichung $\sigma= 0,1\,\text{cm}.$
Zeige, dass ein Bolzen mit einer Wahrscheinlichkeit von $0,8186$ eine Länge zwischen $9,9\,\text{cm}$ und $10,2\,\text{cm}$ besitzt.
Einem Lager werden $12$ Bolzen zufällig entnommen.
Ermittle die Wahrscheinlichkeit dafür, dass darunter mindestens $10$ Bolzen eine Länge zwischen $9,9\,\text{cm}$ und $10,2\,\text{cm}$ besitzen.
Es werden $10$ Bolzen mit einer Länge zwischen $9,9\,\text{cm}$ und $10,2\,\text{cm}$ benötigt.
Bestimme, wie viele Bolzen dem Lager mindestens entnommen werden müssen, damit mit einer Wahrscheinlichkeit von mindestens $98\,\%$ die $10$ benötigten Bolzen enthalten sind.

Erreichbare BE-Anzahl: 7

Bildnachweise [nach oben]

[1]

1.1

Lage des Punkts zeigen

Rechenweg anzeigen

$g(0,00)= 2,20$

Der Punkt $P$ hat also die Koordinaten $P(0,00\mid 2,20).$ Es gilt:

Rechenweg anzeigen

$j(0,00)= 2,20$

Die Koordinaten von $P$ erfüllen also auch die Funktionsgleichung von $j.$ $P$ liegt demnach auf dem Graphen von $j.$

Winkelgröße berechnen

Der Winkel $\alpha$ entspricht dem größeren der beiden Winkel, die die beiden Graphen von $g$ und $j$ im Schnittpunkt $P$ einschließen.

Der Schnittwinkel der beiden Graphen kann mit der entsprechenden Formel berechnet werden. Die Steigung von $g$ kann aus der Funktionsgleichung abgelesen werden: $m_g = 2,8.$
Die Steigung des Graphen von $j$ an der Stelle $x=0,00$ ergibt sich mithilfe der ersten Ableitung:

$\(\begin{array}[t]{rll} j$

Der Schnittwinkel beträgt also:

$\begin{array}[t]{rll} \tan \alpha &=& \dfrac{2,8+0,07}{1-0,07\cdot 2,8} &\quad \scriptsize \mid\; \tan^{-1} \\[5pt] \alpha&\approx& 74,4^{\circ} \end{array}$

Da dies aber kein stumpfer Winkel ist, ist der Gegenwinkel zu $\alpha$ gesucht:

$\alpha = 180^{\circ}- 74,4^{\circ} = 105,6^{\circ}$

Der Winkel $\alpha$ ist ca. $105,6^{\circ}$ groß.

1.2

Die Materialdicke ausgehend vom Punkt $Q$ wird entlang der Geraden $n$ gemessen, die senkrecht zum Graphen von $f$ durch den Punkt $Q$ verläuft.

1. Schritt: Geradengleichung aufstellen

$g(-0,50)= 2,8\cdot (-0,50)+2,20$ $=0,80$

$Q(-0,50\mid g(-0,50))$ $=Q(-0,50 \mid 0,80)$

Damit $n$ senkrecht zu $f$ verläuft, muss für ihre Steigung gelten:

$\begin{array}[t]{rll} m_n\cdot m_f&=& -1 &\quad \scriptsize \mid\;:m_f \\[5pt] m_n&=& -\frac{1}{m_f} &\quad \scriptsize \mid\; m_f = 2,0\\[5pt] m_n &=& -\frac{1}{2,0 } \\[5pt] &=& -0,5 \end{array}$

Mithilfe einer Punktprobe mit den Koordinaten von $Q(-0,50 \mid 0,80)$ ergibt sich für die Gleichung von $n:$

$\begin{array}[t]{rll} y &=& m_n \cdot x + b \\[5pt] 0,80&=& -0,5\cdot (-0,50)+b \\[5pt] 0,8 &=& 0,25 + b \quad \scriptsize \mid\; -0,25 \\[5pt] 0,55 &=& b \end{array}$

Eine Gleichung von $n$ lautet also $n: y = -0,50x +0,55.$

2. Schritt: Schnittpunkt bestimmen

Rechenweg anzeigen

$\begin{array}[t]{rll} f(x)&=& n(x) \\[5pt] x &=& -0,82 \end{array}$

Einsetzen in eine der beiden Gleichungen liefert die zugehörige $y$ -Koordinate:

$\begin{array}[t]{rll} f(-0,82)&=& 2,0\cdot (-0,82) +2,60 \\[5pt] &=& 0,96 \\[5pt] \end{array}$

Die Geraden zu $f$ und $n$ schneiden sich also im Punkt $S(-0,82\mid 0,96).$

3. Schritt: Abstand berechnen

Die Materialdicke entspricht dem Abstand des Schnittpunkts von $n$ und $f$ zum Punkt $Q.$

Rechenweg anzeigen

$d(S,Q)\approx 3,6\,\text{cm}$

Die Materialdicke beträgt ausgehend vom Punkt $Q$ ca. $3,6\,\text{cm}.$

1.3

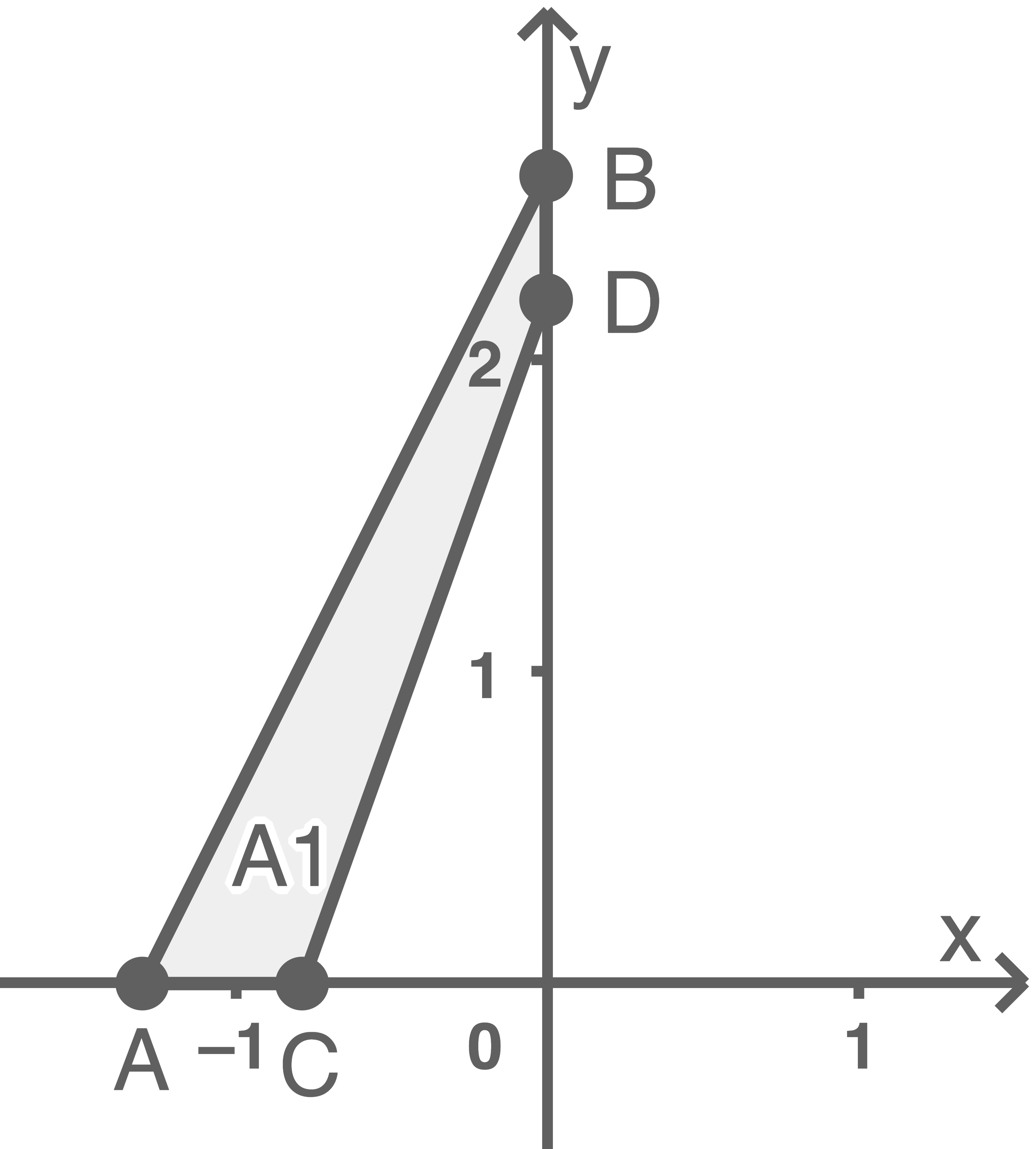
1. Schritt: Inhalt der Querschnittsfläche der Glockenhaube bestimmen

$A\left(-\dfrac{13}{10} \,\bigg \vert \, 0\right) \quad$ $B(0,0\mid 2,6) \quad$ $C\left(-\dfrac{11}{14}\,\bigg \vert \, 0\right) \quad$ $D(0,0\mid 2,2)$

flächeninhalt berechnen, querschnitt, querschnittsfläche

Skizze

Das Dreieck $AOB$ hat den Flächeninhalt:
$\begin{array}[t]{rll} A_{AOB}&=&\dfrac{1}{2} \cdot \dfrac{13}{10} \cdot 2,60 \\[5pt] &=& 1,69 \end{array}$
Das Dreieck $COD$ hat den Flächeninhalt:
$\begin{array}[t]{rll} A_{COD}&=&\dfrac{1}{2} \cdot \dfrac{11}{14} \cdot 2,20 \\[5pt] &=& \dfrac{121}{140} \end{array}$

$\begin{array}[t]{rll} A_1&=& 2\cdot \left(A_{AOB}-A_{COD}\right) \\[5pt] &=& 2\cdot \left( 1,69 -\dfrac{121}{140} \right) \\[5pt] &=& \dfrac{289}{175} \end{array}$

2. Schritt: Inhalt der Querschnittsfläche des Glockenkörpers bestimmen

$\blacktriangleright$ TI nspire CAS

menu $\to$ 4: Analysis $\to$ 3: Integral

$\blacktriangleright$ Casio Classpad II

keyboard $\to$ Math2 $\to$ $\int_{\Box}^{\Box}\Box$

Rechenweg anzeigen

$A_2=7,14$

3. Schritt: Gesamtflächeninhalt bestimmen

Insgesamt ergibt sich:

$\begin{array}[t]{rll} A&=& A_1+ A_2 \\[5pt] &\approx& \frac{289}{175}+7,14 \\[5pt] &\approx& 8,79\,\text{[FE]} \end{array}$

Da eine Längeneinheit $10\,\text{cm}$ entspricht, beträgt der Flächeninhalt der Querschnittsfläche der Glocke ca. $8,79\,\text{dm}^2.$

1.4

1. Schritt: Volumen der Glockenhaube berechnen

Die Glockenhaube bildet einen Kegel, aus dem ein kleinerer Kegel herausgelöst wird.

Der größere Kegel entsteht im Modell durch Rotation der Geraden $f$ und besitzt daher den Radius $r_f=2,6$ und die Höhe $h_f = \dfrac{13}{10}.$ Das Volumen ergibt sich daher zu:
$\begin{array}[t]{rll} V_f&=& \dfrac{1}{3}\cdot \pi \cdot r_f^2 \cdot h_f \\[5pt] &=& \dfrac{1}{3}\cdot \pi \cdot 2,6^2 \cdot \dfrac{13}{10} \\[5pt] &=& \dfrac{2.197}{750}\pi \\[5pt] \end{array}$
Der kleinere Kegel entsteht im Modell durch Rotation der Geraden $g$ und besitzt daher den Radius $r_g=2,2$ und die Höhe $h_g = \dfrac{11}{14}.$ Das Volumen ergibt sich daher zu:
$\begin{array}[t]{rll} V_g&=& \dfrac{1}{3}\cdot \pi \cdot r_g^2 \cdot h_g \\[5pt] &=& \dfrac{1}{3}\cdot \pi \cdot 2,2^2 \cdot \dfrac{11}{14} \\[5pt] &=& \dfrac{1.331}{1.050}\pi \\[5pt] \end{array}$

Das Volumen der Glockenhaube beträgt also:

$\begin{array}[t]{rll} V_{\text{Haube}}&=& V_f -V_g \\[5pt] &=& \dfrac{2.197}{750}\pi- \dfrac{1.331}{1.050}\pi \\[5pt] &\approx& 5,22 \end{array}$

2. Schritt: Volumen des Glockenkörpers berechnen

Der Glockenkörper besteht im Modell ebenfalls aus einem größeren Rotationskörper, aus dem ein kleinerer Rotationskörper herausgelöst wird.

Der äußere Rotationskörper entsteht durch Rotation von $h$ und $k.$ Mit dem Taschenrechner folgt:

Rechenweg anzeigen
$V_{h,k}\approx 304,13$

$\begin{array}[t]{rll} V_{h,k}&=& \pi \cdot \displaystyle\int_{0}^{7,11}\left(h(x)\right)^2\;\mathrm dx + \pi\cdot \displaystyle\int_{7,11}^{7,9}\left(k(x)\right)^2\;\mathrm dx \\[5pt] &\approx& \pi\cdot \left( 78,832+ 17,975\right) \\[5pt] &\approx& 304,13 \\[5pt] \end{array}$
Der innere Rotationskörper entsteht durch Rotation von $j,$ sodass sein Volumen wie oben berechnet werden kann:
$\begin{array}[t]{rll} V_{j}&=& \pi \cdot \displaystyle\int_{0}^{7,90}\left(j(x)\right)^2\;\mathrm dx \\[5pt] &\approx& 232,97 \\[5pt] \end{array}$

Das Volumen des Glockenkörpers beträgt also:

$\begin{array}[t]{rll} V_{\text{Körper}}&=& V_{h,k} -V_j \\[5pt] &=& 304,13- 232,97 \\[5pt] &=& 71,16 \end{array}$

3. Schritt: Masse berechnen

Das Gesamtvolumen der Glocke beträgt:

$\begin{array}[t]{rll} V_{\text{Gesamt}}&=& V_{\text{Haube}} + V_{\text{Körper}} \\[5pt] &=& 5,22 \,\text{[VE]} + 71,16 \,\text{[VE]} \\[5pt] &=& 76,38\,\text{[VE]} \\ &=& 76,38\,[\text{dm}^3]\\ &=& 76\,380 \,[\text{cm}^3] \end{array}$

Mit der Dichte ergibt sich dann die Masse der Glocke:

$\begin{array}[t]{rll} m&=& 76\,380\,\text{cm}^3 \cdot 8,5 \,\dfrac{\text{g}}{\text{cm}^3}\\[5pt] &\approx& 649\,230\,\text{g} \\[5pt] &\approx& 649\,\text{kg} \end{array}$

Die Gesamtmasse der Glocke beträgt ca. $649\,\text{kg}.$

1.5

Mittelwert aller Innendurchmesser vergleichen

1. Schritt: Mittelwert aller Innendurchmesser berechnen

Der Innendurchmesser des Glockenkörpers an der Stelle $x$ wird durch die Funktion $d(x)=2\cdot j(x)$ beschrieben. Mit der in der Aufgabenstellung angegebenen Formel und dem CAS ergibt sich:

Rechenweg anzeigen

$\overline{d} \approx 5,93\,\left[\text{dm}\right]$

2. Schritt: Innendurchmesser bestimmen

Der Innendurchmesser an der Stelle $x=3,95$ ergibt sich mithilfe des CAS zu:

$\begin{array}[t]{rll} d(3,95)&=& 2\cdot j(3,95) \\[5pt] &\approx& 5,40 \,\left[\text{dm}\right] \end{array}$

Der Mittelwert aller Innendurchmesser des Glockenkörpers entspricht also nicht dem Innendurchmesser an der Stelle $x=3,95.$

Mittelwert mit dem arithmetischen Mittel vergleichen

1. Schritt: Kleinsten und Größten Innendurchmesser bestimmen

Mit dem Taschenrechner können Minimum und Maximum des Graphen von $d$ berechnet werden.

$\blacktriangleright$ TI nspire CAS

menu $\to$ 6: Graph analysieren $\to$ 3: Maximum / Minimum

$\blacktriangleright$ Casio Classpad II

Analyse $\to$ Grafische Lösung $\to$ Maximum / Minimum

Der Graph von $d$ besitzt im Intervall $[0,00;7,90]$ einen Tiefpunkt mit den Koordinaten $T(0,7\mid 4,351)$ und keinen Hochpunkt. Der kleinste Innendurchmesser des Glockenkörpers beträgt also $d_{min} \approx 4,35\,\text{dm}.$ Der größte Innendurchmesser ergibt sich durch einen Vergleich der Intervallränder:

$\begin{array}[t]{rll} d(0,00)&=& 4,40 \\[5pt] d(7,90)&\approx& 9,54 \end{array}$

Der größte Innendurchmesser des Glockenkörpers beträgt also $d_{max}\approx 9,54 \,\text{dm}.$

2. Schritt: Arithmetisches Mittel berechnen und vergleichen

$\begin{array}[t]{rll} \dfrac{9,54+4,35}{2}&=& 6,95 \,[\text{dm}] \end{array}$

Das arithmetische Mittel aus kleinstem und größtem Innendurchmesser beträgt ca. $6,95\,\text{dm}$ und stimmt daher nicht mit dem Mittelwert aller Innendurchmesser von $5,93\,\text{dm}$ überein.

1.6

1. Schritt: Koordinaten des Anschlagpunkts bestimmen

Der Klöppel kann durch ein Geradenstück beschrieben werden. Die Gerade ist eine Tangente $t$ an den Graphen von $j$ im Anschlagpunkt $A$ und verläuft durch den Koordinatenursprung $O.$

Die Tangente $t$ hat die Steigung $\(m_t = j$ und als $y$ -Achsenabschnitt Null, da sie durch den Koordinatenursprung verläuft. Außerdem verläuft sie durch den Punkt $A(x_a\mid j(x_a)).$ Es gilt also folgende Gleichung für $t:$

$\(\begin{array}[t]{rll} y&=& j$

Es ist:

$\begin{array}[t]{rll} j(x)&=& 0,05x^2-0,07x+2,20 \\[5pt] j‘(x)&=& 0,1x-0,07 \end{array}$

Einsetzen in die Tangentengleichung liefert:

Rechenweg anzeigen

$\(\begin{array}[t]{rll} j(x_a)&=& j$

Die zugehörige $y$ -Koordinate ist $j(6,63) \approx 3,94,$ also $A(6,63\mid 3,94).$

2. Schritt: Abstand und Teilverhältnis berechnen

Die Strecke von der Befestigung bis zum Anschlagpunkt entspricht dem Abstand von $A$ und $O.$

$\begin{array}[t]{rll} d(O,A)&=& \sqrt{6,63^2+3,94^2} \\[5pt] &\approx& 7,71\,\left[\text{dm} \right] \\[5pt] &\approx& 77\,[\text{cm}] \end{array}$

Der Klöppel ist insgesamt $100\,\text{cm}$ lang.

$100\,\text{cm}-77\,\text{cm}=23\,\text{cm}$

Der Anschlagpunkt teilt den Klöppel also ungefähr im Verhältnis $77:23.$

1.7

Für jede Glocke muss eine der folgenden Möglichkeiten gelten:

Die Glocke hat einen Klangfehler.
Die Glocke hat einen optischen Fehler.
Die Glocke hat einen Klangfehler und einen optischen Fehler.
Die Glocke hat keinen optischen Fehler und keinen Klangfehler.

Die Summe der jeweiligen Anteile muss daher $100\,\%$ betragen. Wenn für 4. ein Anteil von $70\,\%$ gilt, müssen sich die restlichen $30\,\%$ auf 1. -3. verteilen.
Gibt es aber Glocken, die beide Fehler haben, so überschneidet sich der Anteil von $10\,\%$ der optischen Fehler mit dem Anteil von $20\,\%$ der Klangfehler, sodass die Summe nicht $100\,\%$ ergibt.

Die Auffassung der Gießerei ist also falsch, wenn beide Fehler auf derselben Glocke auftreten können.

1.8

Wahrscheinlichkeit nachweisen

Betrachtet wird die Zufallsgröße $L,$ die die zufällige Länge eines Bolzens beschreibt. Diese ist laut Aufgabenstellung normalverteilt mit $\mu = 10,0\,\text{cm}$ und $\sigma = 0,1\,\text{cm}.$

Die gesuchte Wahrscheinlichkeit lässt sich mithilfe des CAS bestimmen:

$\blacktriangleright$ TI nspire CAS

menu $\to$ 5 $\to$ 5 $\to$ E: Binomial Cdf

$\blacktriangleright$ Casio Classpad II

Interaktiv $\to$ Verteilungsfunktionen $\to$ Diskret $\to$ binomial CDf

$\begin{array}[t]{rll} P(9,9\leq L \leq 10,2)&\approx& 0,8186 \\[5pt] \end{array}$

Wahrscheinklichkeit ermitteln

Die Zufallsgröße $X$ beschreibt die zufällige Anzahl der Bolzen mit einer Länge zwischen $9,9\,\text{cm}$ und $10,2\,\text{cm}.$ $X$ ist binomialverteilt mit $n=12$ und $p= 0,8186.$
Die gesuchte Wahrscheinlichkeit kann mithilfe des CAS berechnet werden.

$\begin{array}[t]{rll} P(X\geq 10)&=& 1- P(X\leq 9) \\[5pt] &\approx& 1- 0,3752 \\[5pt] &=& 0,6248 \\[5pt] \end{array}$

Mit einer Wahrscheinlichkeit von ca. $62,48\,\%$ besitzen unter $12$ Bolzen mindestens $10$ die gewünschte Länge.

Anzahl der Bolzen berechnen

Gesucht ist nun ein $n,$ sodass Folgendes gilt:
$n$ soll nun so bestimmt werden, dass folgende Gleichung erfüllt ist:

$\begin{array}[t]{rll} P(X\geq 10)&\geq& 0,98 \\[5pt] 1-P(X\leq 9)&\geq& 0,98 &\quad \scriptsize \mid\;-1 \\[5pt] -P(X\leq 9)&\geq& -0,02 &\quad \scriptsize \mid\;\cdot (-1) \\[5pt] P(X\leq 9)&\leq& 0,02 \end{array}$

Systematisches Ausprobieren mit dem CAS liefert:

$\begin{array}[t]{rll} n=15& P(X\leq 9) &\approx& 0,0400 \\[5pt] n=20& P(X\leq 9) &\approx& 0,0002 \\[5pt] n=17& P(X\leq 9) &\approx& 0,0060 \\[5pt] n=16& P(X\leq 9) &\approx& 0,0160 \\[5pt] \end{array}$

Es müssen also mindestens $16$ Bolzen aus dem Lager entnommen werden, damit mit einer Wahrscheinlichkeit von mindestens $98\,\%$ $10$ Bolzen mit der richtigen Länge dabei sind.