Pflichtbereich

In den Teilaufgaben 1.1 bis 1.5 ist von den jeweils fünf Auswahlmöglichkeiten genau eine Antwort richtig. Kreuze das jeweilige Feld an.

1.1

Für welchen Wert $t$ hat der zum Punkt $A(-4\mid t\mid 4)$ gehörende Ortsvektor den Betrag $9?$

	$t=0$
	$t=1$
	$t=7$
	$t=9$
	$t=49$

1.2

Der Punkt $B(-1\mid2\mid 3)$ wird an der Ebene $x=1$ gespiegelt. Der Spiegelpunkt $\(B$ besitzt die Koordinaten:

	$\(B$
	$\(B$
	$\(B$
	$\(B$
	$\(B$

1.3

Der Punkt $C$ teilt die Strecke $\overline{A B}$ im Verhältnis 1:1. Welche Aussage ist falsch?

	$\overrightarrow{A B}=2 \cdot \overrightarrow{A C}$
	$\overrightarrow{A B}=2 \cdot \overrightarrow{C B}$
	$\overrightarrow{A B}=2 \cdot \overrightarrow{B C}$
	$\overrightarrow{A C}=\overrightarrow{C B}$
	$\overrightarrow{A B}=\overrightarrow{A C}+\overrightarrow{C B}$

1.4

Für welchen Wert $r$ sind die Vektoren $\pmatrix{r\\3\\1}$ und $\pmatrix{1\\2-r\\2}$ orthogonal zueinander?

	$r=1$
	$r=2$
	$r=3$
	$r=4$
	$r=5$

1.5

Die Ebene $2 \cdot x-3 \cdot z=4$

	verläuft durch den Koordinatenursprung.
	enthält den Punkt $(0\mid0\mid1).$
	verläuft parallel zur $y$ -Achse.
	schneidet die $y$ -Achse.
	verläuft parallel zur $x$ - $z$ -Ebene.

(5 BE)

Für einen Wert $a$ ist die in $\mathbb{R}$ definierte Funktion $\(f$ mit $\(f$ die erste Ableitungsfunktion einer ganzrationalen Funktion $f.$

2.1

Der Graph von $f$ hat einen Extrempunkt.
Gib die Art dieses Extrempunkts an.

(1 BE)

2.2

Die Tangente an den Graphen von $f$ im Punkt $(1\mid-1)$ verläuft parallel zur Geraden mit der Gleichung $y=4 \cdot x-2025.$
Ermittle eine Gleichung von $f.$

(4 BE)

Gegeben ist die in $\mathbb{R}$ definierte ganzrationale Funktion $f$ mit $f(x)=\frac{1}{3} \cdot x^3-x.$

3.1

Einer der Graphen I, II und III in der Abbildung stellt den Graphen von $f$ dar.

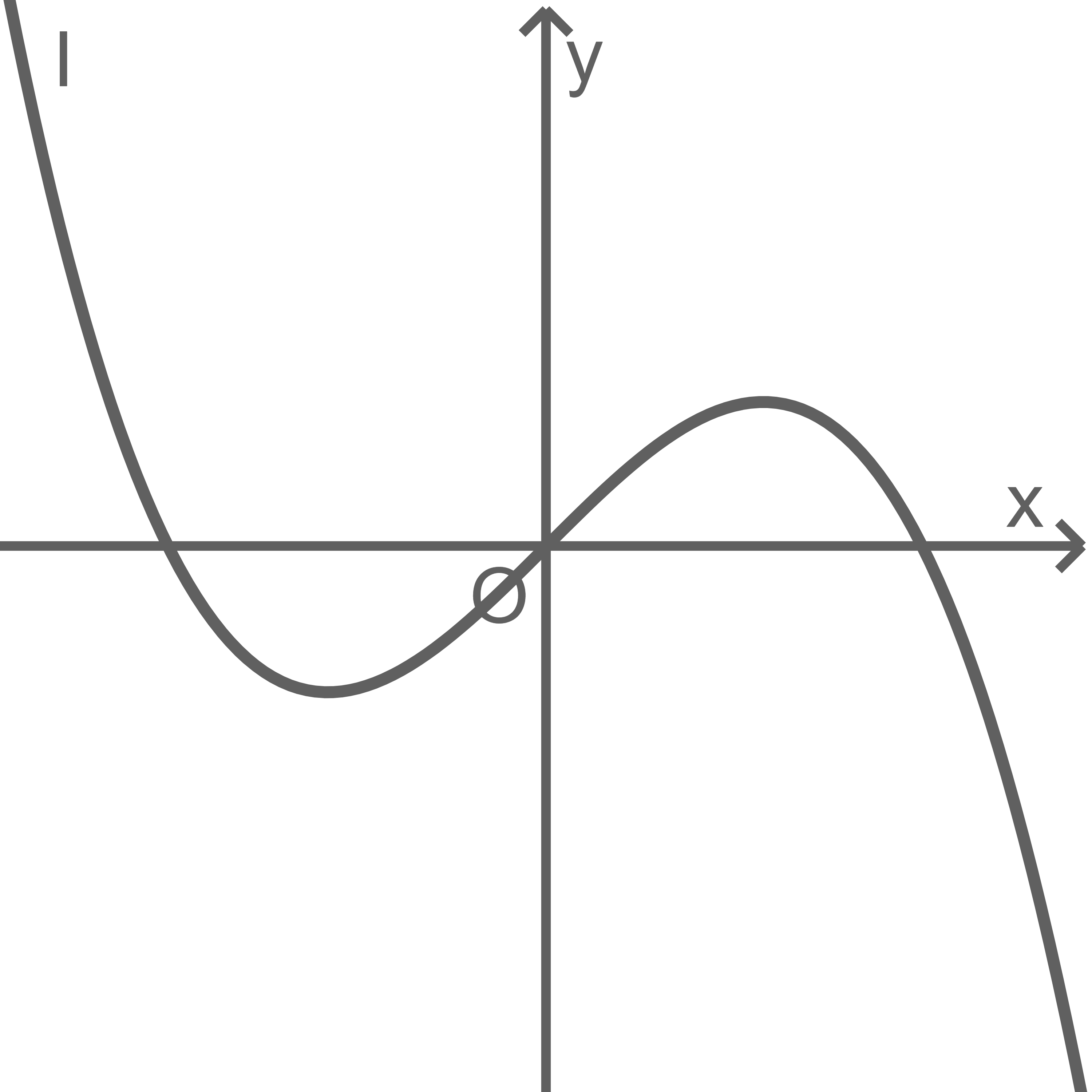
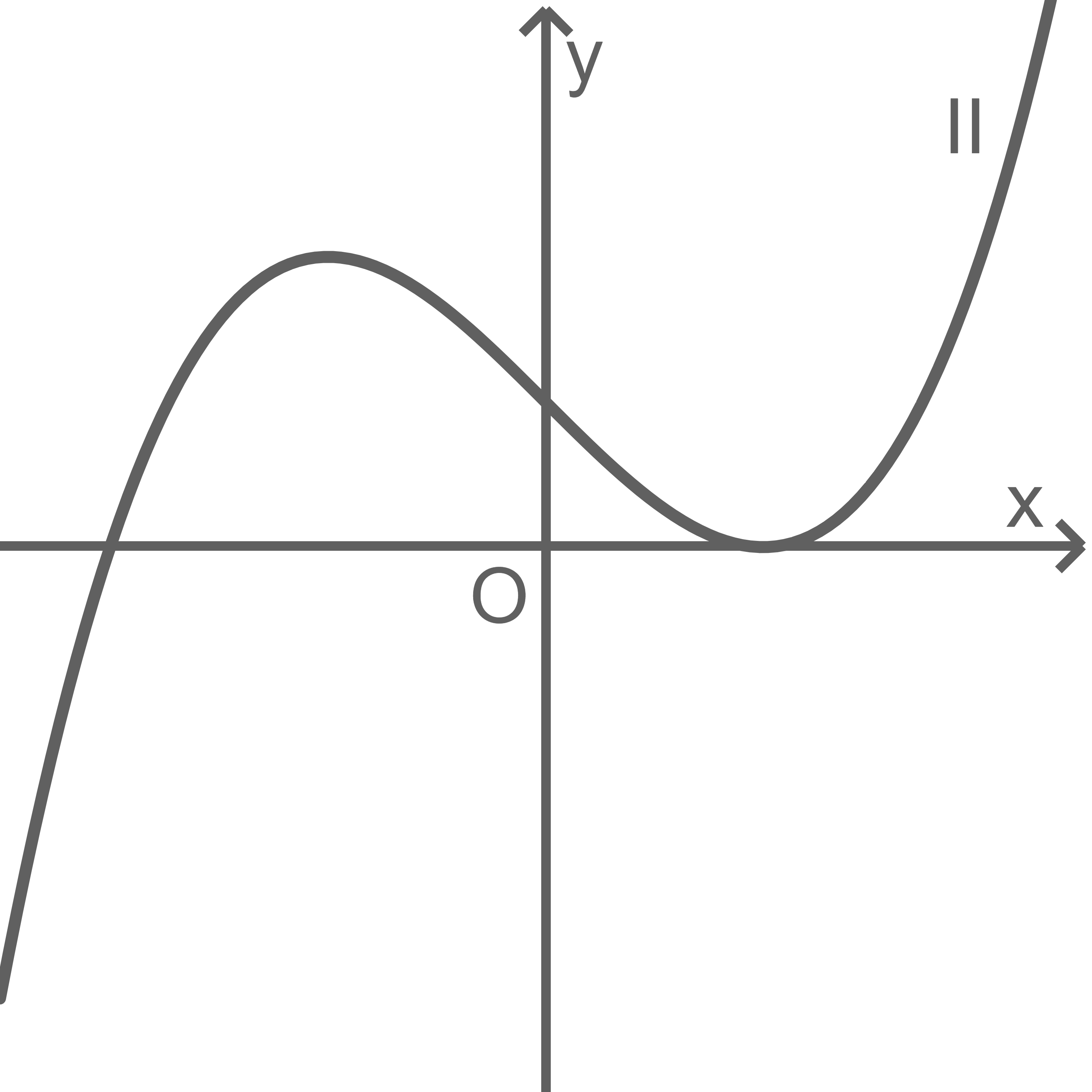
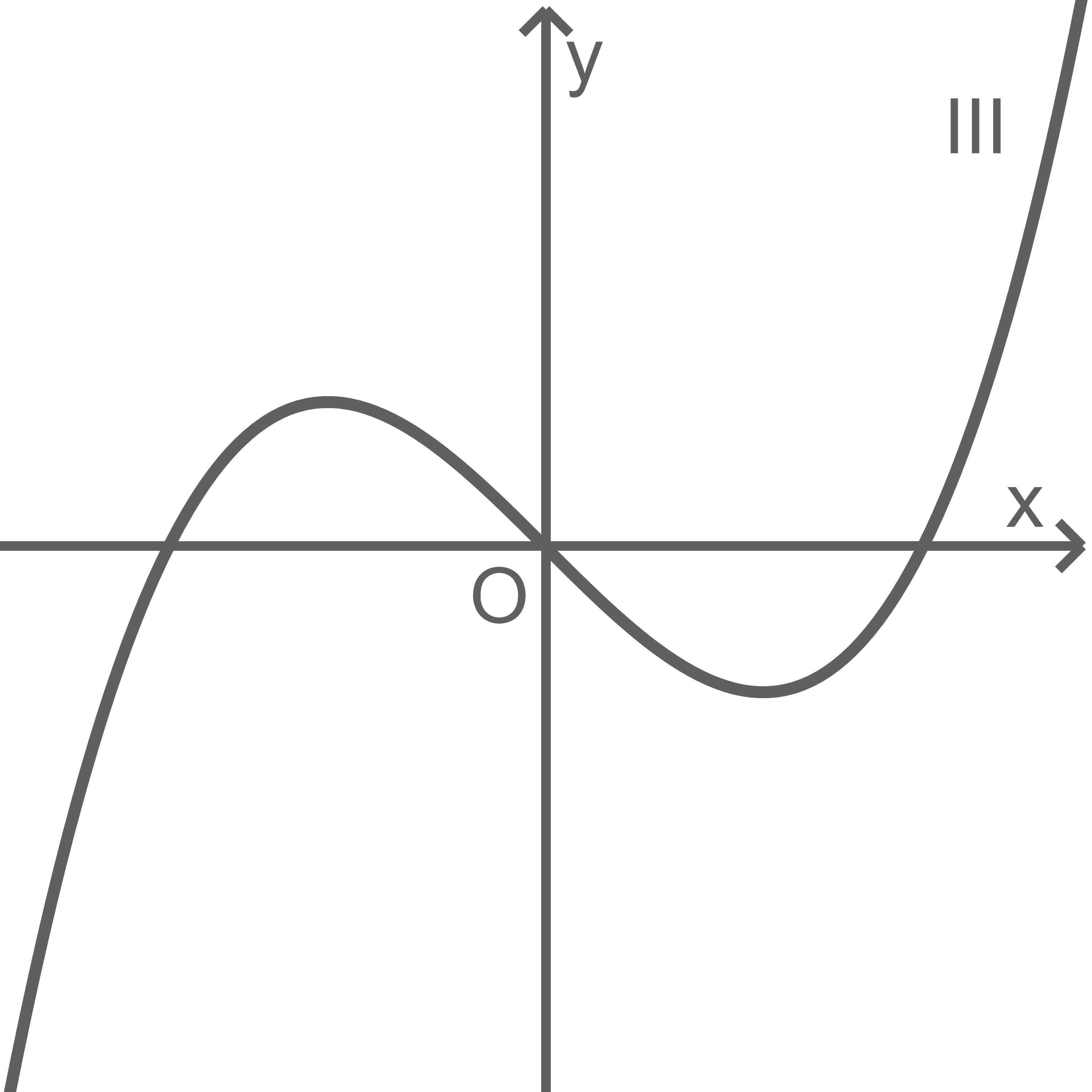
Gib diesen Graphen an und begründe, dass die beiden anderen Graphen dafür nicht infrage kommen.

(3 BE)

3.2

Berechne $\displaystyle\int_{0}^{1}f(x)\;\mathrm dx.$

(2 BE)

Die Abbildung zeigt die Wahrscheinlichkeitsverteilung einer binomialverteilten Zufallsgröße $X$ mit $E(X)=4.$

4.1

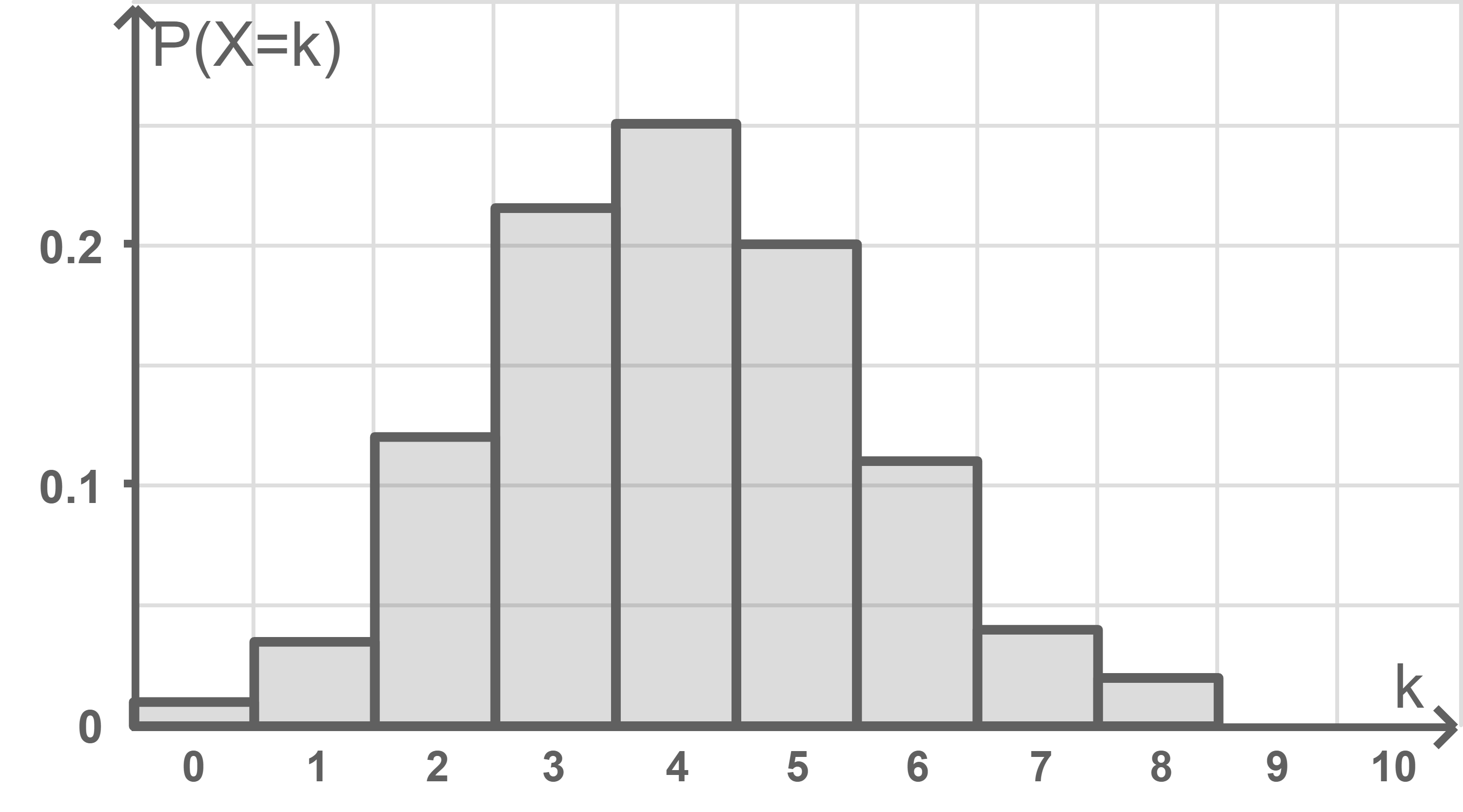
Ermittle unter Verwendung der Abbildung einen Näherungswert für die Wahrscheinlichkeit, dass $X$ um höchstens $1$ vom Erwartungswert abweicht.

(2 BE)

4.2

Beschreibe ein Zufallsexperiment, bei dem die Wahrscheinlichkeit eines Ereignisses mit dem Term $\displaystyle\sum_{k=0}^{5}\pmatrix{10\\k}\cdot 0,4^k \cdot 0,6^{10-k}$ berechnet werden kann.
Gib dieses Ereignis an.

(3 BE)

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?

1.1

$\begin{array}[t]{rlll} \left\vert\pmatrix{-4\\t\\4}\right\vert&=&9 \\[5pt] \sqrt{(-4)^2+t^2+4^2}&=&\sqrt{32+t^2} \\[5pt] \sqrt{32+t^2}&=&9 &\mid\;^2 \\[5pt] 32+t^2&=&81 &\mid\;-32 \\[5pt] t^2&=&49 &\mid\;\sqrt{\;} \\[5pt] t&=&\pm7 \end{array}$

Die dritte Antwort, $t=7,$ ist somit richtig.

1.2

Der Punkt $B$ ist $1-(-1)=2\;\text{LE}$ von der Ebene $x=1$ entfernt. Da sich nur die $x$ -Koordinate um diesen Betrag ändert, besitzt der Spiegelpunkt die Koordinaten $\(B$ Antwort fünf ist somit korrekt.

1.3

Da $C$ die Strecke $\overline{AB}$ teilt, besitzt der Vektor $\overrightarrow{BC}$ eine andere Orientierung als der Vektor $\overrightarrow{AB}.$ Die Gleichung $\overrightarrow{AB}=2\cdot\overrightarrow{BC}$ kann somit nicht stimmen und die dritte Aussage ist falsch.

1.4

$\begin{array}[t]{rlll} \pmatrix{r\\3\\1}\cdot\pmatrix{1\\2-r\\2}&=&0 \\[5pt] r+3\cdot(2-r)+2&=&0 \\[5pt] -2r+8&=&0 &\mid\;-8\\[5pt] -2r&=&-8 &\mid\;:(-2)\\[5pt] r&=&4 \end{array}$

Antwort vier, $r=4,$ ist damit korrekt.

1.5

Die angegebene Ebenengleichung besitzt kein $y$ -Wert und verläuft somit parallel zur $y$ -Achse. Antwort drei ist somit die richtige Antwort.

2.1

Die Funktionsgleichung von $f$ lautet $3x^2+ax+c$ für eine reelle Zahl $c.$ Da der Vorfaktor von $x^2$ positiv ist, ist der Graph eine nach oben geöffnete Parabel und $f$ besitzt somit einen Tiefpunkt.

2.2

Da die Tagente von $f$ im Punkt $(1\mid-1)$ parallel zur Geraden $y=4x-2025$ verläuft, folgt:

$\(\begin{array}[t]{rlll} f$

Einsetzen des Punktes $(1\mid-1)$ in die resultierende Gleichung $f(x)=3x^2-2x+c$ liefert:

$\begin{array}[t]{rlll} 3\cdot1^2-2\cdot1+c&=&-1 \\[5pt] 1+c&=&-1 &\mid\;-1 \\[5pt] c&=&-2 \end{array}$

Die Funktion $f$ besitzt somit die Gleichung $f(x)=3x^2-2x-2.$

3.1

Graph I kommt nicht infrage, da $x^3$ schneller wächst als $x$ und somit $\lim\limits_{x\to+\infty}f(x)=\infty$ gelten muss.

Graph II kommt ebenfalls nicht infrage, da die Funktionsgleichung von $f$ kein konstantes Glied besitzt und somit eine Nullstelle im Koordinatenursprung besitzen muss.

Graph III stellt somit den Graphen von $f$ dar.

3.2

Rechenweg anzeigen

$\displaystyle\int_{0}^{1}f(x)\;\mathrm dx = -\dfrac{5}{12}$

4.1

$P(3\leq X\leq5)\approx0,7$

4.2

Zufallsexperiment beschreiben

Eine Urne enthält sechs weiße und vier schwarze Kugeln. Es wird zehn mal zufällig jeweils eine Kugel mit Zurücklegen aus der Urne gezogen.

Ereignis angeben

Es werden insgesamt höchstens fünf schwarze Kugeln gezogen.

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?