Aufgabe 1: Aufgeblasen
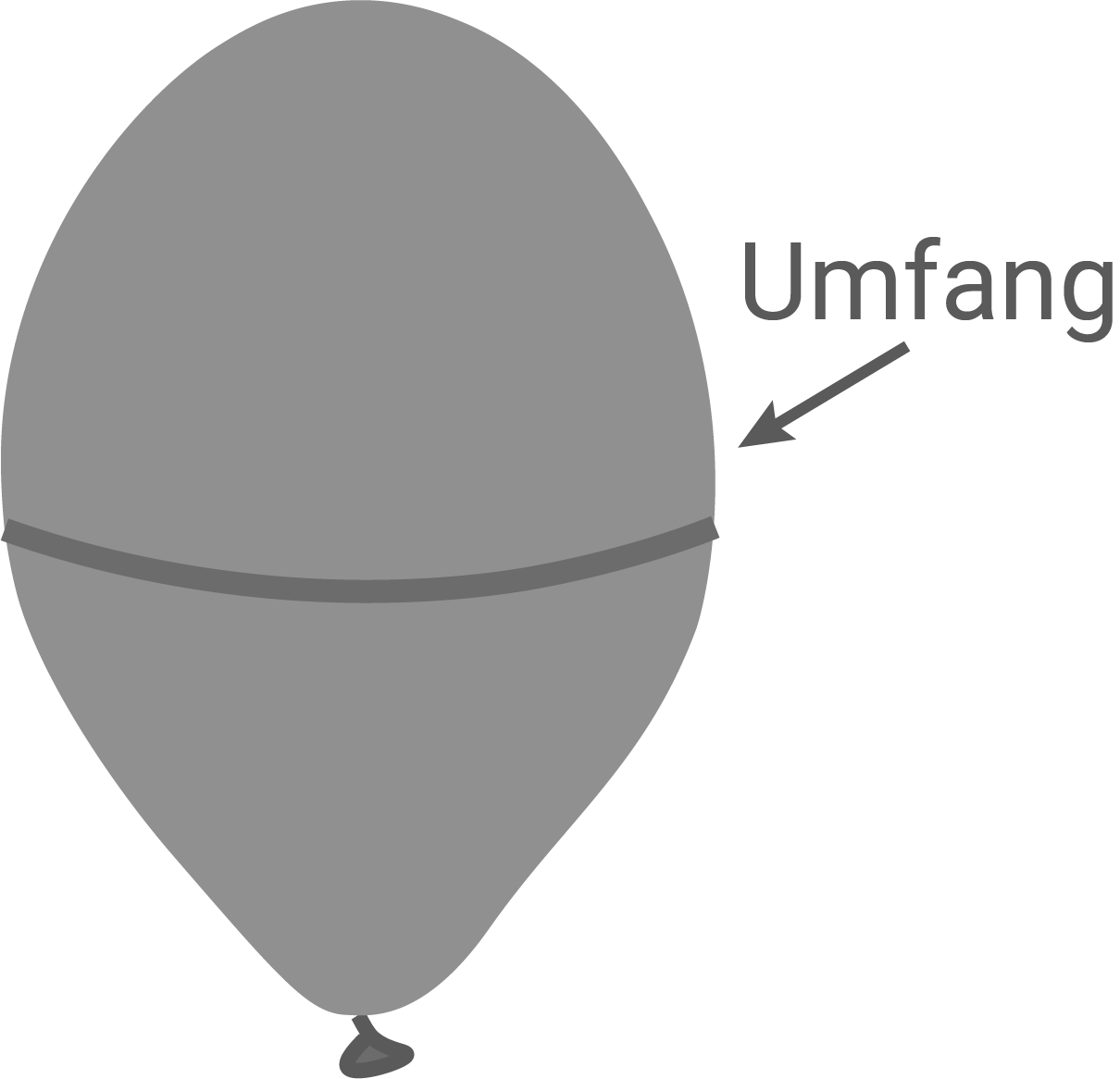
Lino möchte das Volumen eines Luftballons bestimmen. Er misst dafür bei einem Luftballon einen Umfang von 
(Abbildung 1).
Lino betrachtet den Luftballon vereinfacht als Kugel.
Bestätige rechnerisch, dass er so das Volumen des Ballons mit 
abschätzen kann.
Begründe, warum das tatsächliche Volumen des Luftballons größer sein muss als die Abschätzung durch diese Kugel.
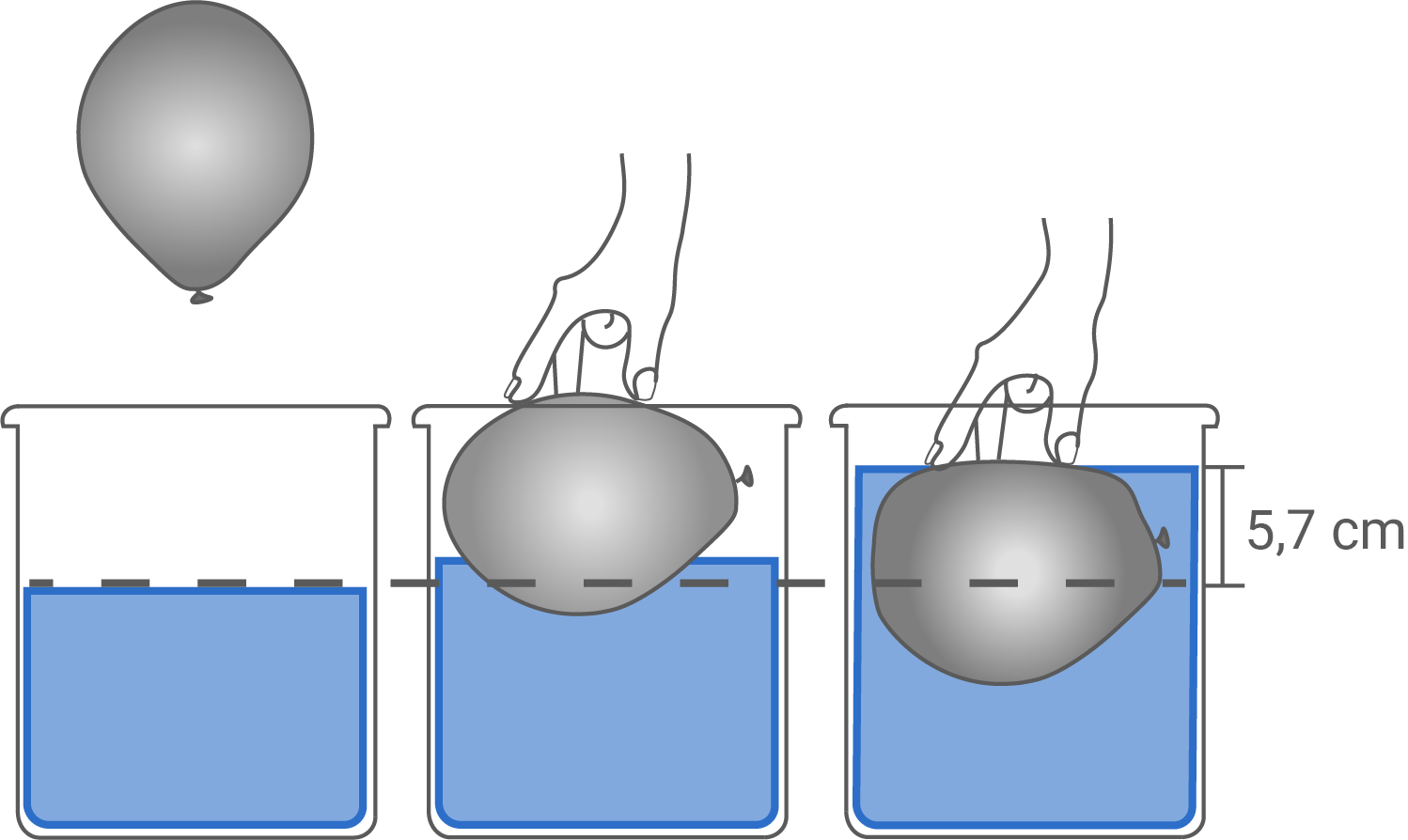
Lino möchte das Volumen des Ballons noch genauer bestimmen. Dafür verwendet er einen Glaszylinder mit einer Grundfläche von 
und füllt 
Wasser hinein.
Berechne die Höhe des Wasserstands in dem Glaszylinder.
Nun taucht Lino den Ballon ganz in das Wasser. Der Ballon verdrängt dabei die Wassermenge, die seinem Volumen entspricht. Dadurch steigt der Wasserspiegel im Zylinder um 
(Abbildung 2).
Zeige, dass der Luftballon ein Volumen von ca. 
hat.
Berechne, um wie viel Prozent das durch eine Kugel abgeschätzte Volumen von 
kleiner ist als das durch Eintauchen bestimmte Volumen von 
(nicht maßstabsgetreu)
Lino möchte zum Geburtstag seines kleinen Bruders einen großen Karton komplett mit Luftballons füllen, die alle jeweils ein Volumen von etwa 
haben.
Er behauptet: „Wenn ich den Rauminhalt des Kartons durch das Volumen eines Ballons teile, weiß ich genau, wie viele Ballons ich brauche.“
Linos Behauptung ist falsch.
Entscheide begründet, ob die Berechnung zu viele oder zu wenige Ballons ergibt.
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?Für den Umfang eines Kreises gilt:
nach 
umstellen:
![\(\begin{array}[t]{rlll}
U&=&2\cdot \pi \cdot r &\mid\;:(2\cdot \pi) \\[5pt]
\dfrac{U}{2\cdot \pi}&=&r \\[5pt]
\dfrac{55,8\;\text{cm}}{2\cdot \pi}&=&r \\[5pt]
r&\approx&8,9\;\text{cm}
\end{array}\)](https://www.schullv.de/resources/formulas/42891e5d0f1be912e910d4fc210fff6b4c92b82b3c465372bdc3418e2b063a2c_light.svg)
Volumen einer Kugel:
![\(\begin{array}[t]{rlll}
V&=&\dfrac{4}{3}\pi \cdot r^{3} \\[5pt]
V&=&\dfrac{4}{3}\pi \cdot (8,9\;\text{cm})^{3} \\[5pt]
V&\approx&2953\;\text{cm}^{3}
\end{array}\)](https://www.schullv.de/resources/formulas/c8e25ed5874f0cdfafde88789b178f7ce21dd2f61f1057413904cba9e9f79a67_light.svg)
Der Luftballon hat keine perfekte Kugelform, sondern ist meist an den Polen gestreckt. Bei gleichem Umfang entsteht dadurch ein größeres Volumen als bei einer Kugel. Die Kugel liefert deshalb nur eine zu kleine Abschätzung.
gegeben: Grundfläche 
Wasservolumen 
Für das Volumen eines Zylinders gilt:
Nach 
umstellen und Werte einsetzen:
Die Höhe des Wasserstandes beträgt etwa 
gegeben: Pegelanstieg 
Grundfläche 
Volumen des Ballons berechnen:
Das Volumen des Luftballons beträgt etwa 
Prozentuale Abweichung berechnen:
Das Kugelvolumen ist etwa 
kleiner.
Beim Einfüllen in den Karton bleibt Luft zwischen den Ballons. Dadurch wird der Karton nicht vollständig mit Ballonvolumen gefüllt. Die Berechnung ergibt daher zu viele Ballons.