Aufgabe 2: Bienen
Das Halten von Bienen wird in Deutschland in den letzten Jahren immer beliebter. Bienen sammeln ihren Honig in Waben, die sie selbst bauen (Abbildung 1).
Waben besteht aus ca. 
Zellen. Eine Zelle kann mit bis zu 
Honig gefüllt sein.
Entscheide rechnerisch, ob 
Waben ausreichen können, um 
Honig zu erhalten.
Jafra - La libertad de ser tú, Junio-dia-de-la-abeja, Bearbeitet von SchulLV, CC BY-SA 4.0
Die Zellen haben annähernd die Form von regelmäßigen Sechsecken (Abbildung 2).
Begründe, dass in jedem der Dreiecke die drei Innenwinkel gleich groß sind.
Leite die Formel
für den Flächeninhalt eines regelmäßigen Sechsecks her.
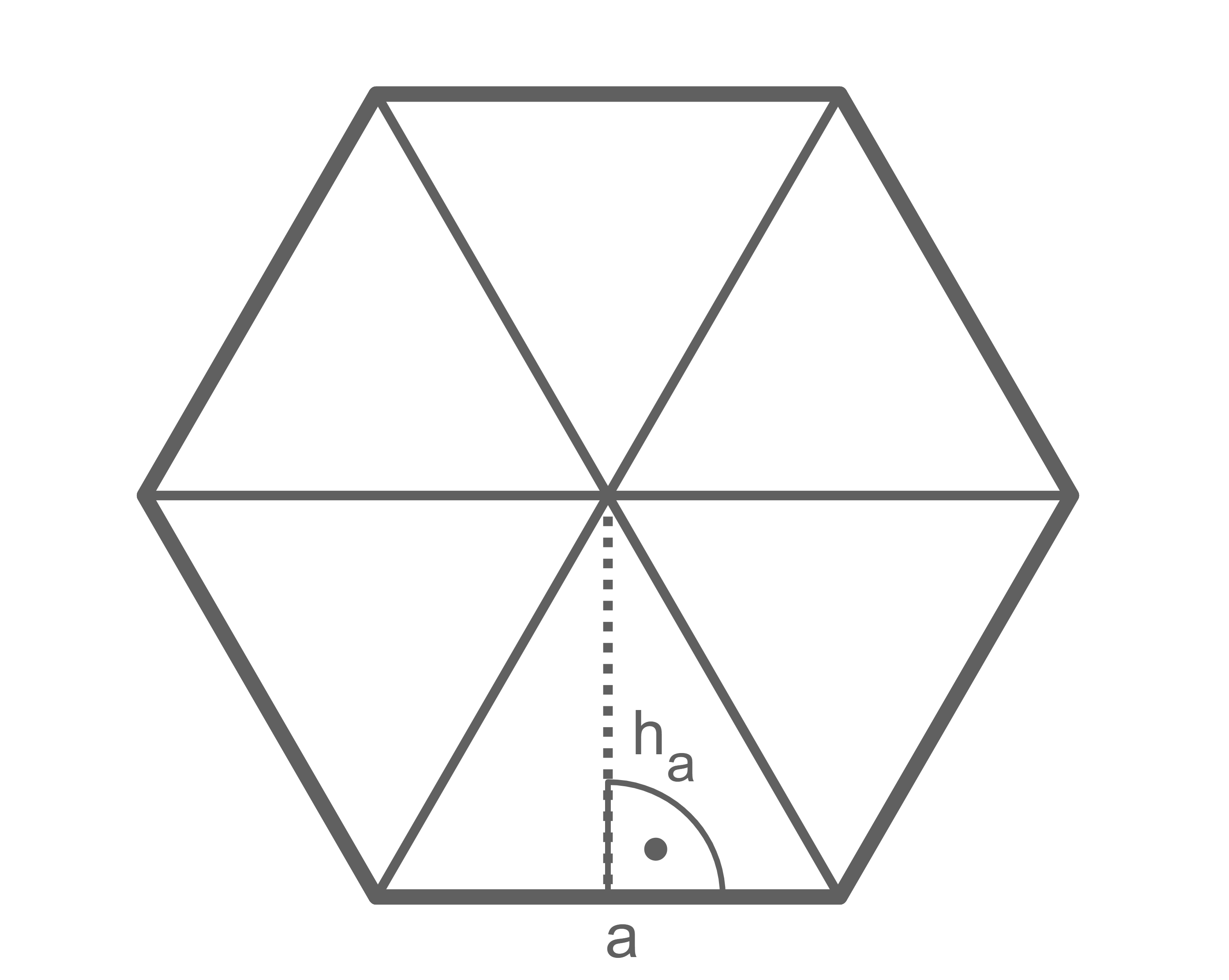
regelmäßiges Sechseck
Den Aufbau von Honigwaben kann man als mathematisches Muster betrachten. Man beginnt mit einer Anfangszelle. Alle anderen baugleichen sechseckigen Zellen werden lückenlos rings um diese Zelle gelegt.
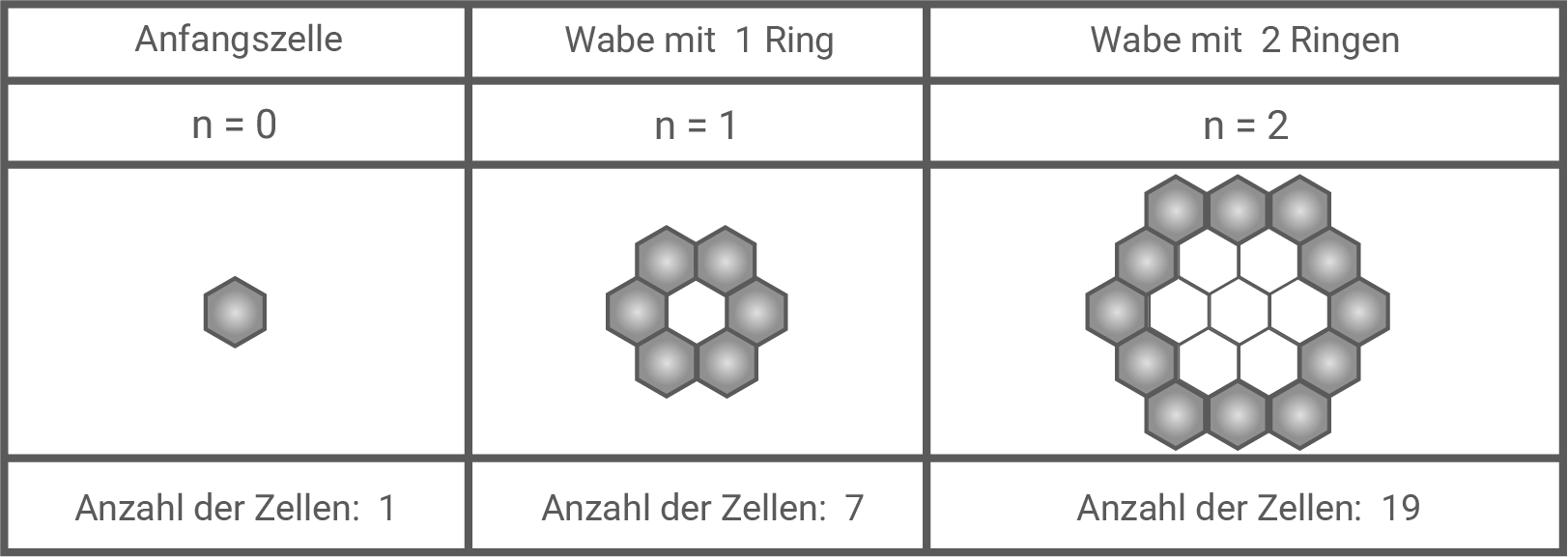
Begründe mithilfe der Abbildung 3, dass die Anzahl der Zellen im Muster nicht linear wächst.
Die Anzahl der Zellen kann mit folgender Formel berechnet werden:
(
: Anzahl an Ringen)
Berechne die Anzahl der Zellen für 
Ringe.
Bestimme rechnerisch die Anzahl der Zellen, die von einer Wabe mit 
Ringen zu einer Wabe mit 
Ringen neu hinzukommen.
Stelle einen allgemeinen Term auf, mit dem du den Zuwachs an Zellen von einer Wabe mit Ringen zur Wabe mit 
Ringen berechnen kannst und vereinfache diesen Term so weit wie möglich.
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?Honigmenge berechnen:
Waben reichen aus, da sie etwa 
Honig enthalten können.
In einem regelmäßigen Sechseck beträgt der Innenwinkel 
Wird das Sechseck durch Verbindung des Mittelpunktes mit den Ecken in sechs gleich große Dreiecke geteilt, wird jeder Innenwinkel halbiert. Dadurch entstehen in jedem Dreieck zwei Winkel von 
Da die Winkelsumme im Dreieck 
beträgt, muss der dritte Winkel in jedem Dreieck also ebenfalls 
betragen.
Höhe eines gleichseitigen Dreiecks:
Dreiecksfläche:
Sechseckfläche:
Die Abstände zwischen den Anzahlen der Zellen vergrößern sich von Ring zu Ring.
Von 
zu 
steigt die Zellzahl stärker als von 
zu 
Da die Zuwächse nicht konstant sind, wächst die Anzahl der Zellen nicht linear.
Bei 
Ringen gibt es 
Zellen.
Es kommen 
Zellen hinzu.
![\(\begin{array}[t]{rlll}
\Delta(n)&=&s_{n+1}-s_n \\[5pt]
&=&(1+3(n+1)+3(n+1)^{2})-(1+3n+3n^{2}) \\[5pt]
&=&(1+3n+3+3n^{2}+6n+3)-(1+3n+3n^{2}) \\[5pt]
&=&7+9n+3n^{2}-1-3n-3n^{2} \\[5pt]
&=&6n+6 \\[5pt]
\Delta(n)&=&6(n+1)
\end{array}\)](https://www.schullv.de/resources/formulas/6a9903a3606296db5658e184bf898e8421f3aeb6cc7d7cd6b24f35ec00fc6195_light.svg)
Der Zuwachs von auf 
Ringe beträgt immer 
Zellen.