Aufgabe 3: Dreieck und Parabel

Meltem zeichnet durch die Punkte $A(-3\mid 0),\,\ B(3\mid 0)$ und $C(0\mid 4,5)$ das gleichschenklige Dreieck $ABC$
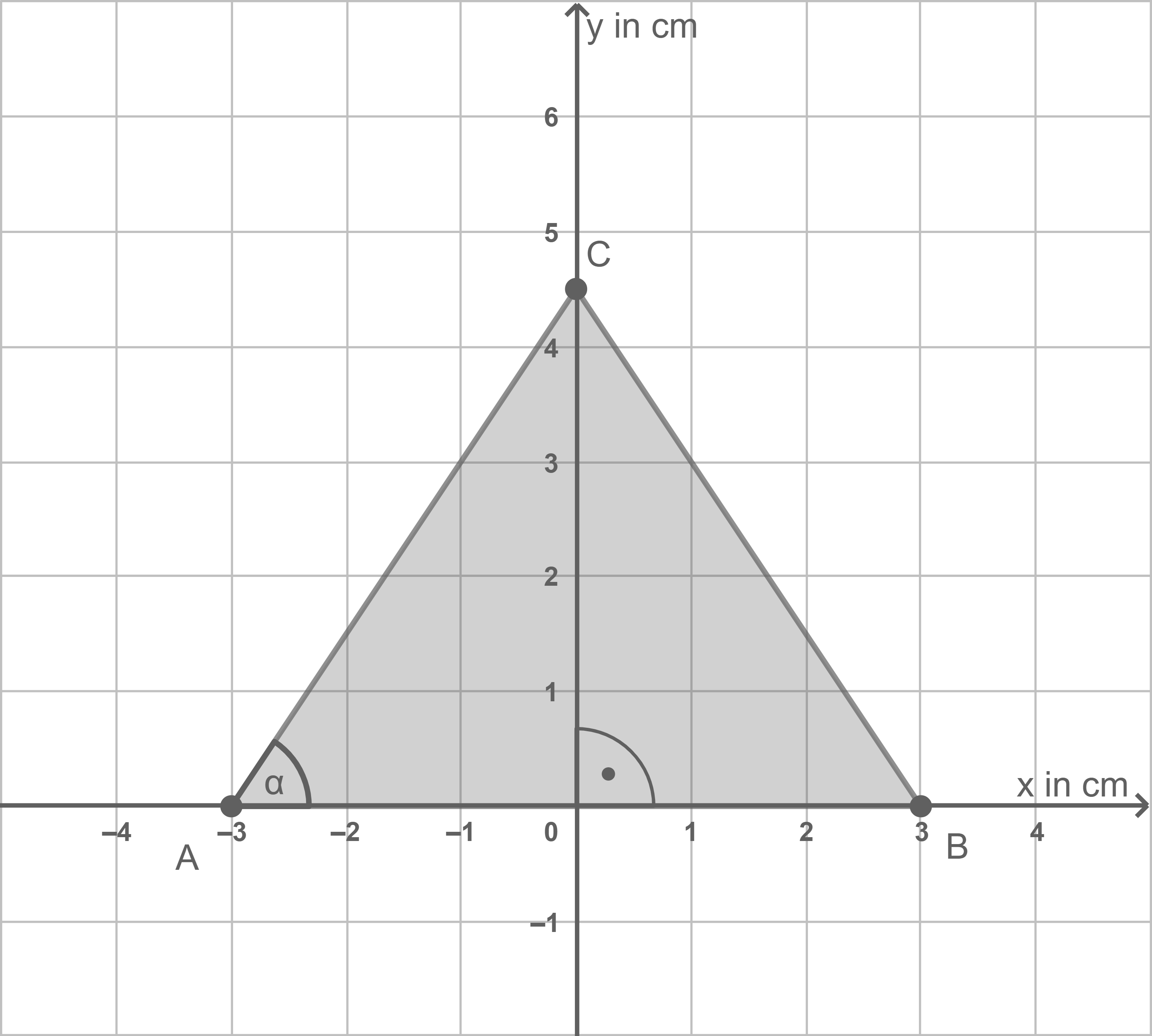
(Abbildung 1).

Berechne den Flächeninhalt des Dreiecks.

Bestimme den Umfang des Dreiecks.

Berechne die Größe des Winkels $\alpha.$

Koordinatensystem mit schattiertem Dreieck, Punkte A(-3,0), B(3,0), C(0,5), Winkel α an A

Abbildung 1: Dreieck

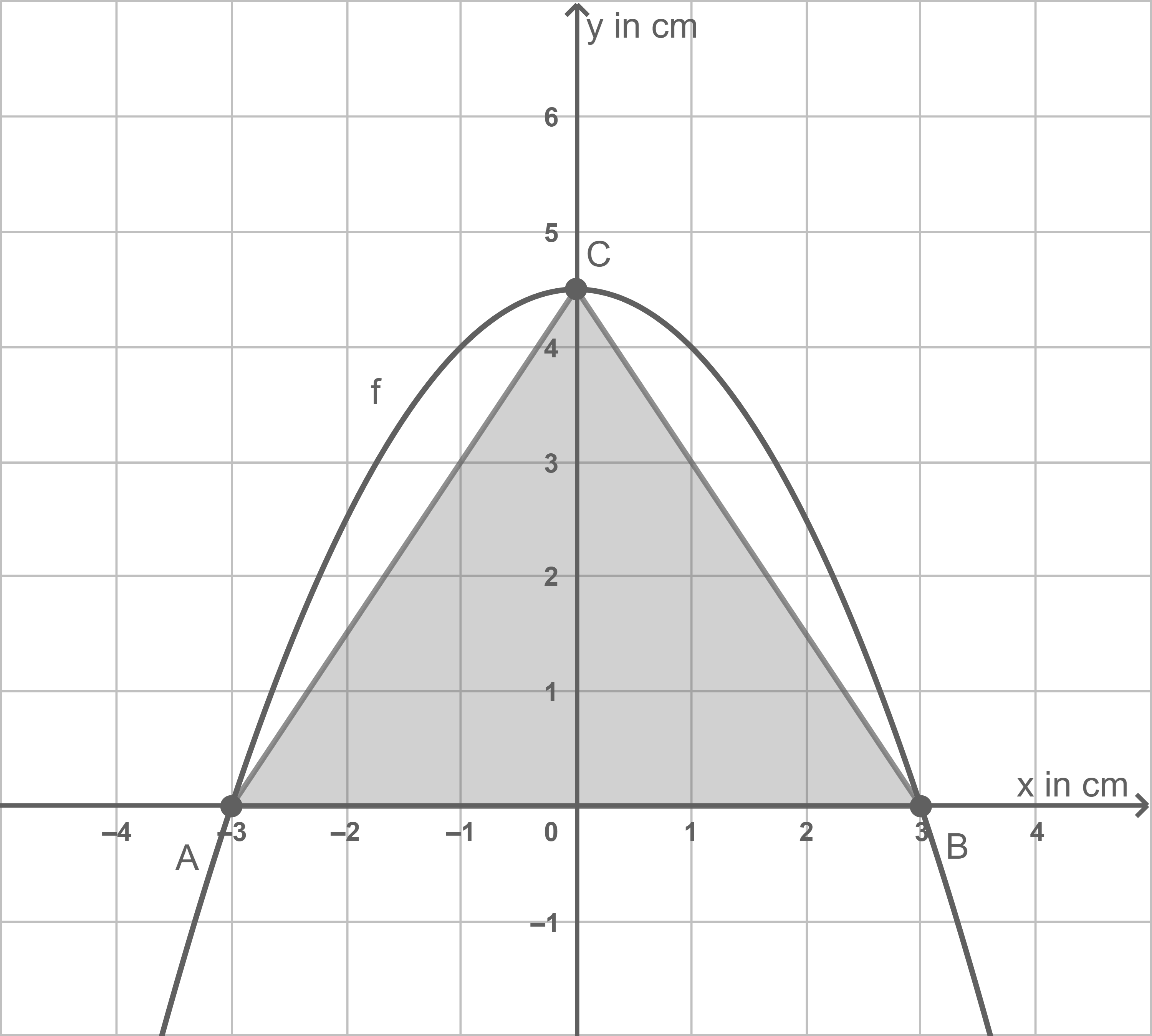
Meltem zeichnet über dem Dreieck die Parabel $f.$
Die Parabel verläuft durch die Punkte $A$ und $B$ sowie den Punkt $C$ als Scheitelpunkt (Abbildung 2).

Begründe, dass die Funktionsgleichung
$f(x)=a\cdot (x+3)\cdot (x-3)$ zu der Parabel passt und $a \lt0$ sein muss.

Bestimme den Wert des Faktors $a$ mithilfe des Punktes $C.$

Koordinatensystem mit schattiertem Dreieck zwischen A(-3,0), B(3,0), C(0,5) und Parabel f

Abbildung 2: Dreieck und Parabel

Meltem verschiebt nun den Punkt $C$ entlang der
$y$ -Achse. Die Parabel verläuft weiterhin durch die drei
Punkte $A,$ $B$ und $C.$ Beurteile die folgenden Aussagen. Kreuze an.

	richtig	falsch
Verschiebt Meltem den Punkt $C$ auf der $y$ -Achse nach oben, wird die Parabel gestaucht.		
Verschiebt Meltem den Scheitelpunkt $C$ auf den Punkt $(0\mid -1),$ ist die Parabel nach oben geöffnet.		
Der Flächeninhalt des Dreiecks bleibt unverändert, wenn Meltem den Punkt $C$ entlang der $y$ -Achse verschiebt.		

Meltem möchte nun erreichen, dass das Dreieck $ABC$ einen rechten Winkel bei $C (0\mid 4,5)$ hat und zugleich die drei Punkte $A,$ $B$ und $C$ eine neue Parabel festlegen. Sie möchte aber nur die Lage der Punkte $A$ und $B$ verändern.

(1)

Beschreibe eine Möglichkeit, die Lage der Punkte $A$ und $B$ zu wählen, und bestimme für diesen Fall die Koordinaten von $A$ und $B.$

(2)

Bestimme die Funktionsgleichung der Parabel durch die drei Punkte.

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?

Grundseite $g$ berechnen:

$AB= \left| 3\;\text{cm}-(-3\;\text{cm})\right|=6\;\text{cm}$

Höhe $h:$

$h=y_c=4,5\;\text{cm}$

Formel Flächeninhalt Dreieck:

$A=\frac{1}{2}\cdot g\cdot h$

$g$ und $h$ einsetzen:

$A=\frac{1}{2}\cdot 6\;\text{cm}\cdot 4,5\;\text{cm}=13,5\;\text{cm}^{2}$

Rechtwinkliges Dreieck bilden mit:

Grundseite $g:$ $A$ zur Mitte der Seite $AB$
Höhe $h:$ senkrechte Strecke vom Punkt $C$ zur Grundseite

$AC$ mit Hilfe des Satz des Pythagoras bestimmen:

$AC^{2}=g^{2}+h^{2}$

$\begin{array}[t]{rlll} AC&=&\sqrt{(0\;\text{cm}-(-3\;\text{cm}))^{2}+(4,5\;\text{cm}-0\;\text{cm})^{2}} \\[5pt] &=&\sqrt{9\;\text{cm}^{2}+20,25\;\text{cm}^{2}} \\[5pt] &\approx&5,41\;\text{cm} \end{array}$

Da $ABC$ gleichschenklig ist:

$BC=AC$

Umfang $U$ berechnen:

Rechenweg anzeigen

$U\approx 16,82\;\text{cm}$

$\begin{array}[t]{rlll} \sin(\alpha)&=&\dfrac{h}{AC} \\[5pt] \sin(\alpha)&=&\dfrac{4,5\;\text{cm}}{5,41\;\text{cm}} \\[5pt] \sin(\alpha)&\approx&0,83 \;\text{cm} \\[5pt] \alpha &=& \sin^{-1}(0,83\;\text{cm}) \\[5pt] \alpha &\approx&56,1^\circ \end{array}$

Nullstellen aus der Zeichnung ablesen:

$x=3$ und $x=-3$

Eine Parabel mit den Nullstellen $-3$ und $3$ hat die allgemeine Form:

$f(x)=a(x+3)(x-3)$

Der Scheitelpunkt liegt bei $C$ oberhalb der $x$ -Achse, was bedeutet das die Parabel nach unten geöffnet ist und $a$ negativ sein muss. Denn der Faktor $a$ legt fest, in welche Richtung die Parabel geöffnet ist.

Punkt $C$ in $f(x)$ einsetzen, um $a$ zu erhalten:

$4,5=a(0+3)(0-3)$

$4,5=-9a$

$a=-\dfrac{1}{2}$

Daraus ergibt sich folgende Gleichung:

$f(x)=-\dfrac{1}{2}(x+3)(x-3)$

	richtig	falsch
Verschiebt Meltem den Punkt $C$ auf der $y$ -Achse nach oben, wird die Parabel gestaucht.		
Verschiebt Meltem den Scheitelpunkt $C$ auf den Punkt $(0\mid -1)$ , ist die Parabel nach oben geöffnet.		
Der Flächeninhalt des Dreiecks bleibt unverändert, wenn Meltem den Punkt $C$ entlang der $y$ -Achse verschiebt.		

Falsch, weil eine größere Höhe die Parabel streckt, nicht staucht.
Richtig, da bei $C(0 \mid -1)$ der Faktor $a \gt 0$ ist.
Falsch, weil sich die Höhe des Dreiecks und damit sein Flächeninhalt ändert.

(1)

Da das Dreieck symmetrisch zur $y$ -Achse ist und der Scheitelpunkt $C(0\mid 4,5)$ oberhalb der $x$ -Achse liegt, müssen die Punkte $A$ und $B$ denselben Abstand von der $y$ -Achse haben wie $C$ in der Höhe. Deshalb werden $A(-4,5\mid 0)$ und $B(4,5\mid 0)$ gewählt.So entsteht bei $C$ ein rechter Winkel.