Wahlaufgaben
Wahlaufgabe Arithmetik/Algebra
Gib das Ergebnis in Stunden an.
Löse die Gleichung.
Karl möchte den großen Tank seines Autos vollständig auffüllen.
Zehn Liter sind noch im Tank.
Am Morgen kostet ein Liter Diesel und am Abend nur
Berechne die Einsparung, wenn Karl am Abend statt am Morgen tankt.
Sein Auto verbraucht durchschnittlich Diesel auf
Ermittle die Strecke, die Karl mit dem vollen Tank seines Autos maximal zurücklegen kann.
Wahlaufgabe Geometrie 1
Das rechteckige Dach eines Schuppens ist lang und
breit.
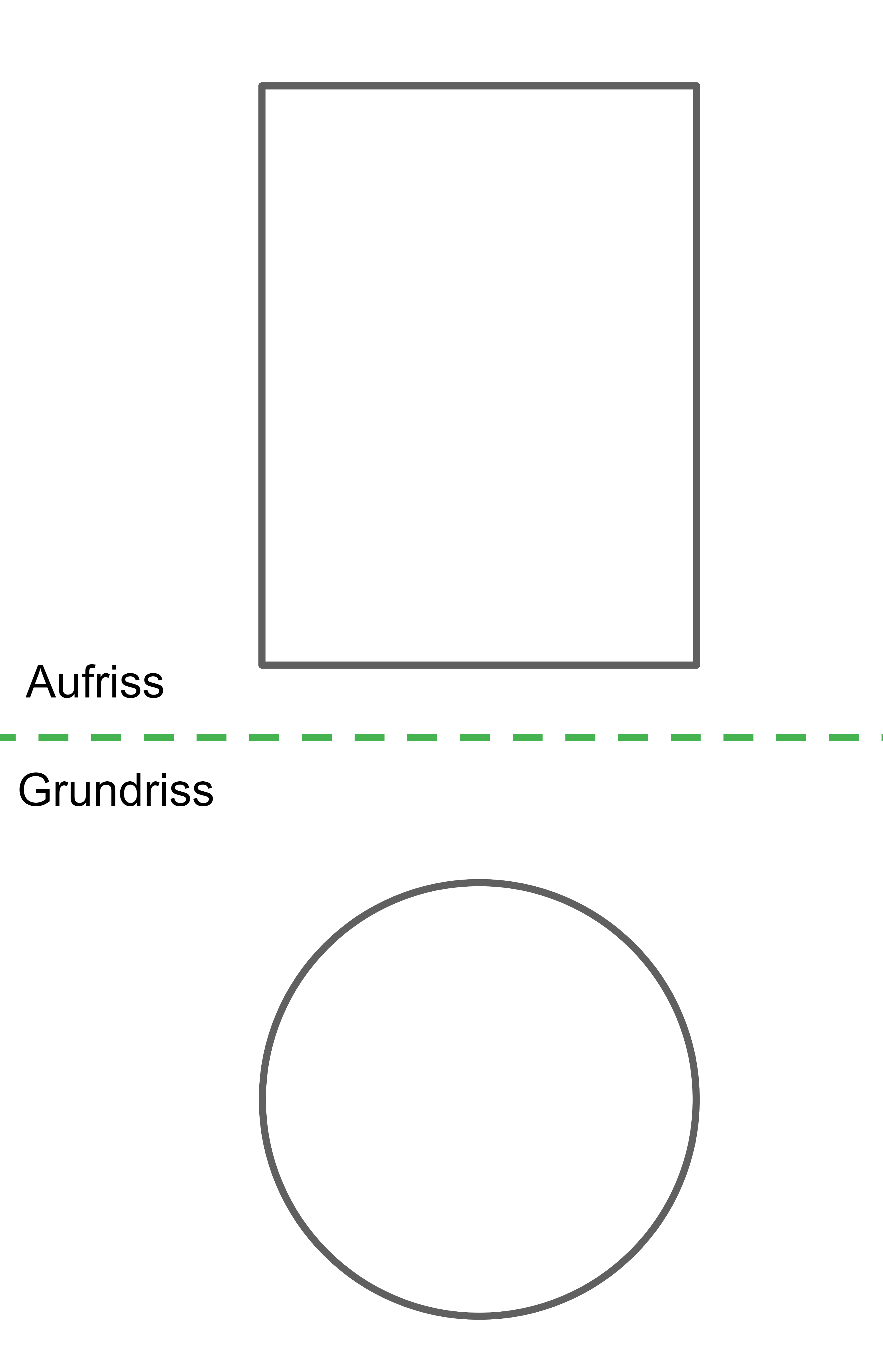
Das Regenwasser wird in einem Regenfass aufgefangen. Das leere, zylinderförmige Regenfass hat einen Durchmesser von und ist
hoch.
Bei einem kräftigen Regen sind Regenwasser je Quadratmeter auf das Dach gefallen.

Zeige rechnerisch, dass die Regentonne das gesamte Regenwasser von diesem Dach aufnehmen kann.
Stelle die Regentonne im Zweitafelbild in einem geeigneten Maßstab auf unliniertem Papier dar.
Wahlaufgabe Stochastik
In einer 5. Klasse wurde gezählt, wie viele Farbstifte die Schülerinnen und Schüler täglich mitbringen. Die Ergebnisse wurden notiert.
| Mädchen | Anzahl der Farbstifte |
| Maria | |
| Janina | |
| Laura | |
| Hanna | |
| Lena | |
| Tina | |
| Kristina |
| Jungen | Anzahl der Farbstifte |
| Jacob | |
| Erik | |
| Max | |
| John | |
| Jannik | |
| Nico |
Stelle die Gesamtanzahl der Farbstifte der Mädchen und die Gesamtanzahl der Farbstifte der Jungen in einem Diagramm dar.
Gib die Spannweite für die Anzahl der Farbstifte der Mädchen an.
Berechne das arithmetische Mittel für die Anzahl der Farbstifte der Mädchen.
Erik und Max haben die Verteilung der Farbstifte der Jungen in einem Kreisdiagramm dargestellt.
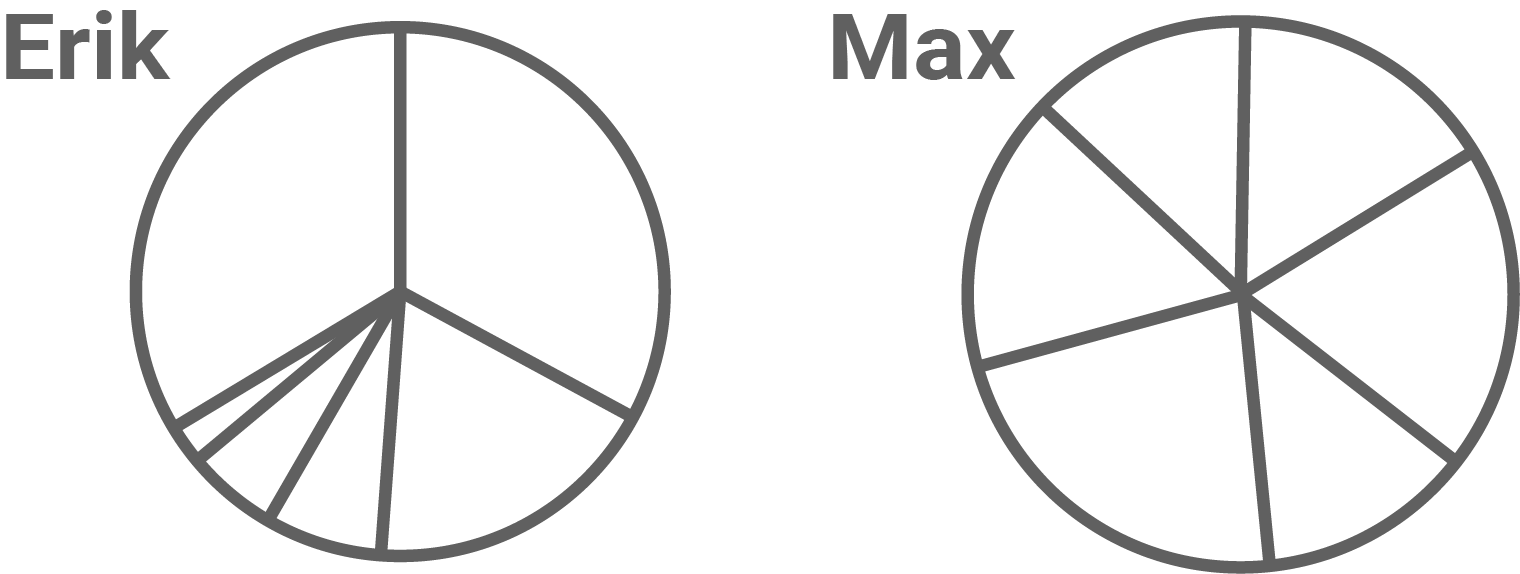
Eines der Kreisdiagramme ist richtig dargestellt.
Begründe, welches Diagramm falsch ist.
Kerstin hat einen gestreiften Strumpf.
In einer Schublade befinden sich fünf gestreifte und acht gepunktete Strümpfe.
Sie nimmt wahllos einen heraus und zieht diesen an.
Gib die Wahrscheinlichkeit dafür an, dass Kerstin jetzt einen gestreiften und einen gepunkteten Strumpf trägt.
Wahlaufgabe Geometrie 2
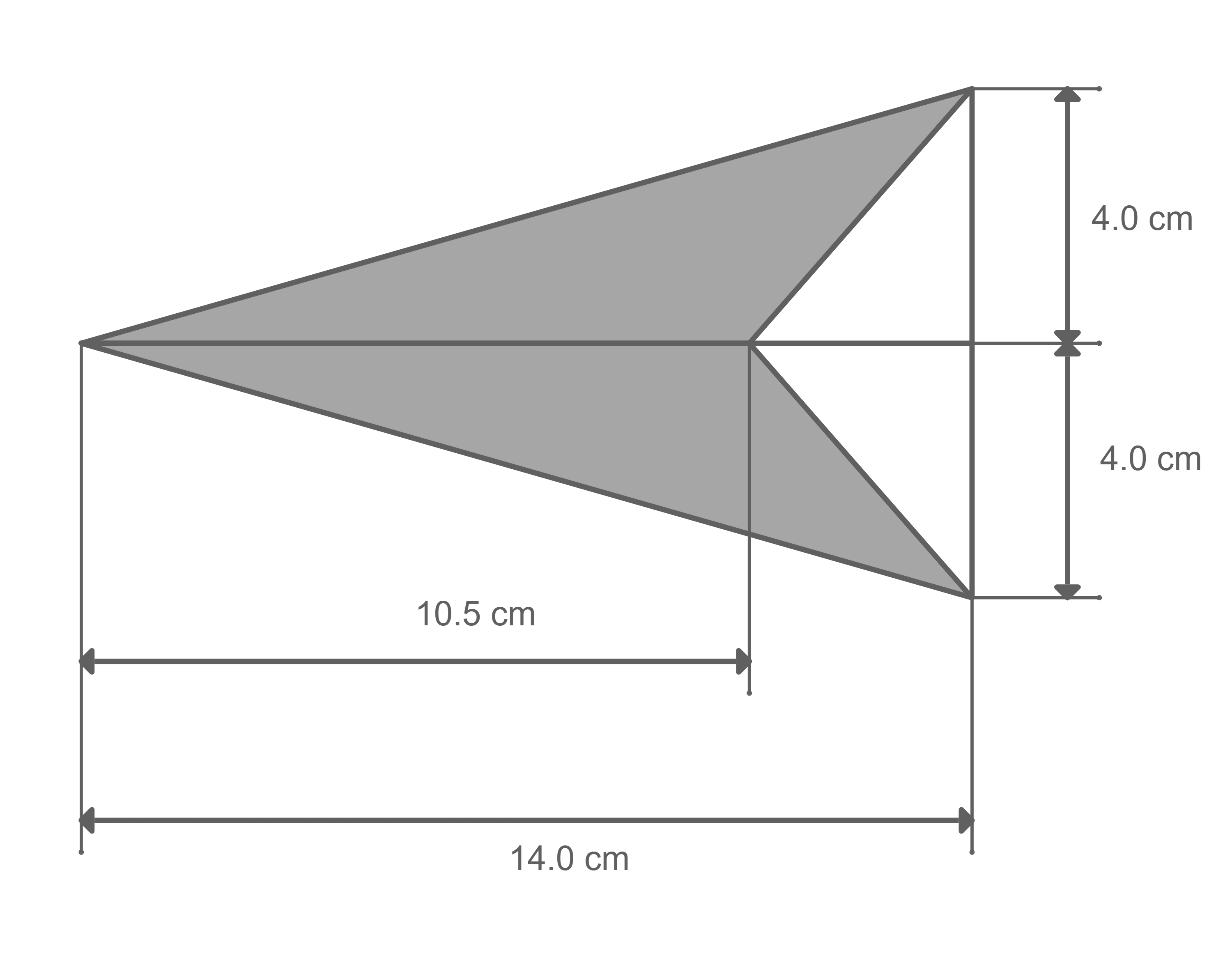
Die Figur ist Teil eines Logos an der Wand einer Schule.
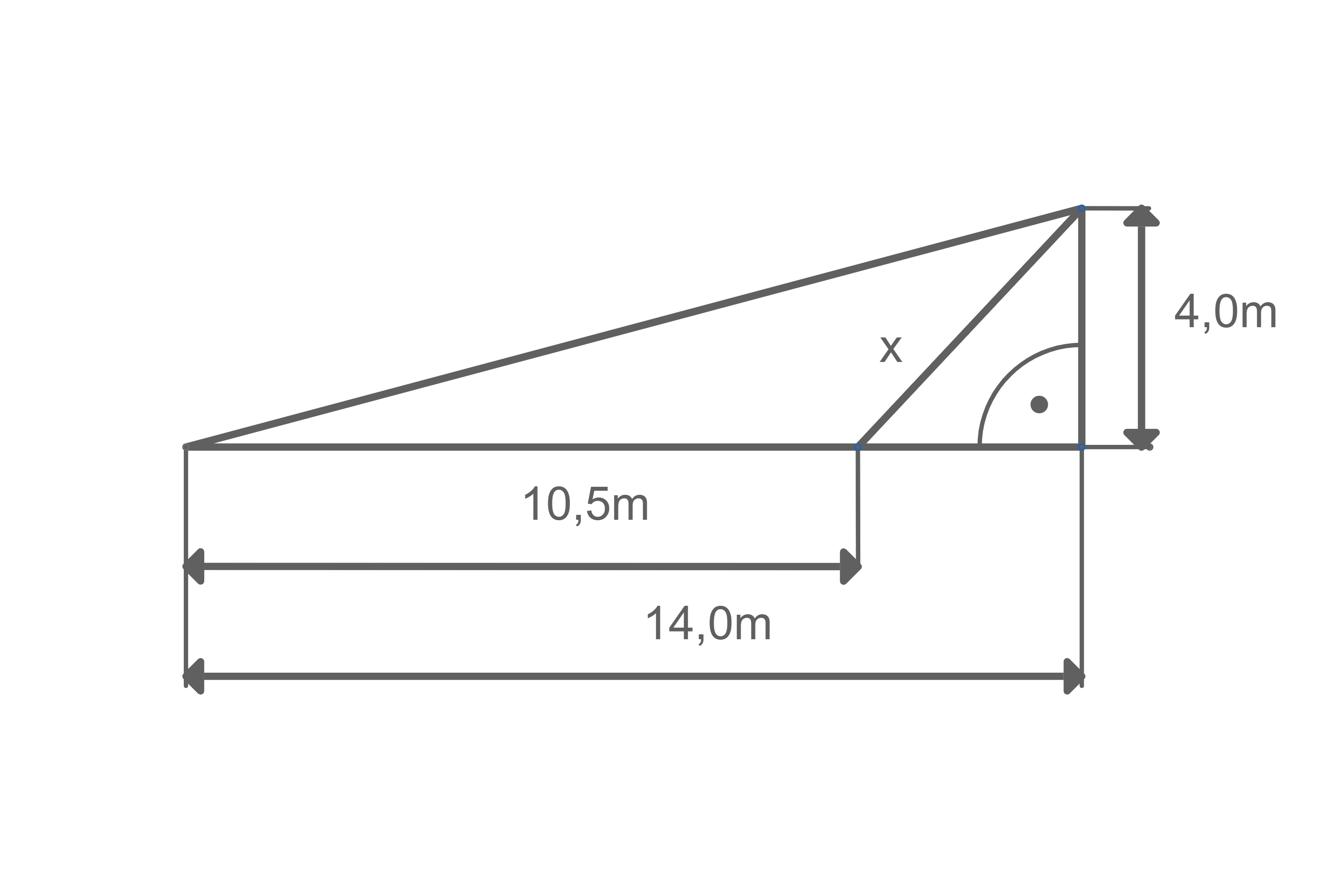
Berechne die Länge der Seite
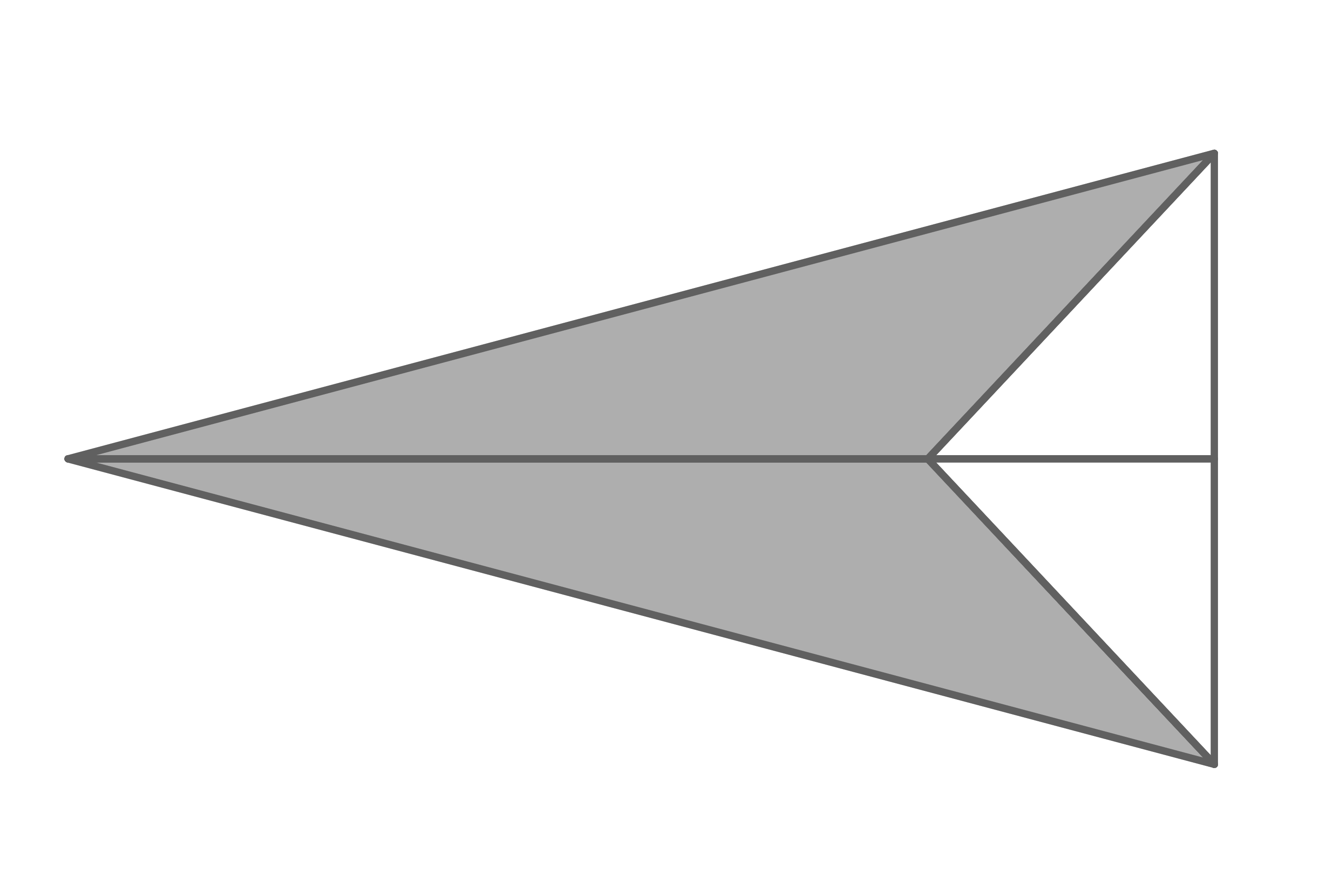
Im gesamten Logo muss die grau dargestellte Fläche neu gestrichen werden. Dafür liegen zwei Angebote vor.
Angebot Firma A: Festpreis
Angebot Firma B: je Quadratmeter und
Gerüst
Zeige rechnerisch, dass das Angebot der Firma B günstiger ist.
Zeichne das Schullogo im Maßstab auf unliniertem Papier.
Wahlaufgabe Funktionen
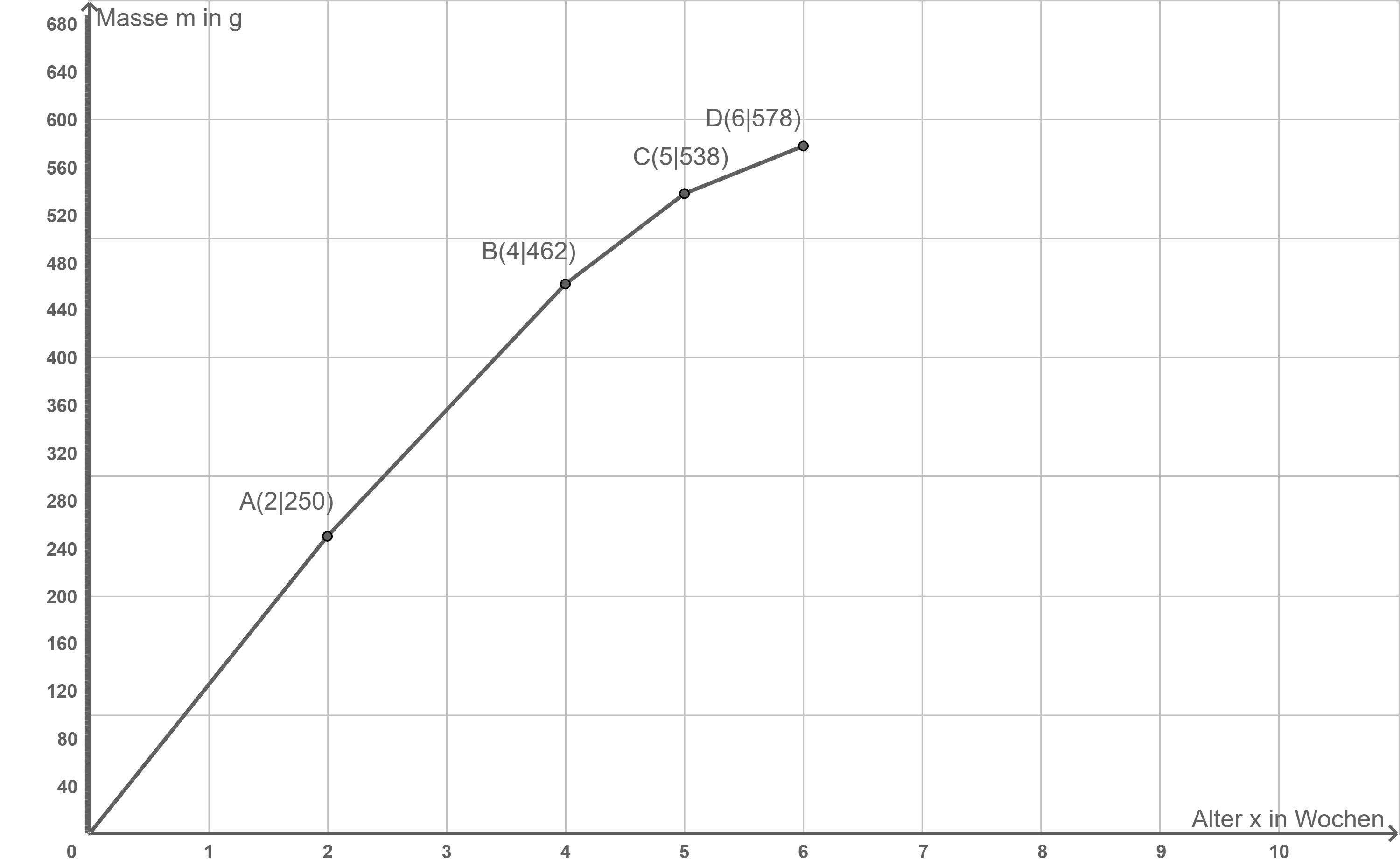
.jpg)
| Alter |
Masse |
Stelle die Masse in Abhängigkeit vom Alter in einem Koordinatensystem graphisch dar.
Jens hat den Term aufgestellt, mit dem er die Masse
Katzenbabys berechnen kann. Für
setzt er dazu das Alter in Wochen ein.
Zeige an einem Beispiel, dass der Term für die Berechnung der gemessenen Werte näherungsweise verwendet werden kann.
Berechne die Masse des Katzenbabys zum Zeitpunkt der Geburt. Begründe, dass der Term für diese Berechnung nicht geeignet ist.
Ein Radfahrer und ein Wanderer
bewegen sich aufeinander zu.
(siehe Abbildung)
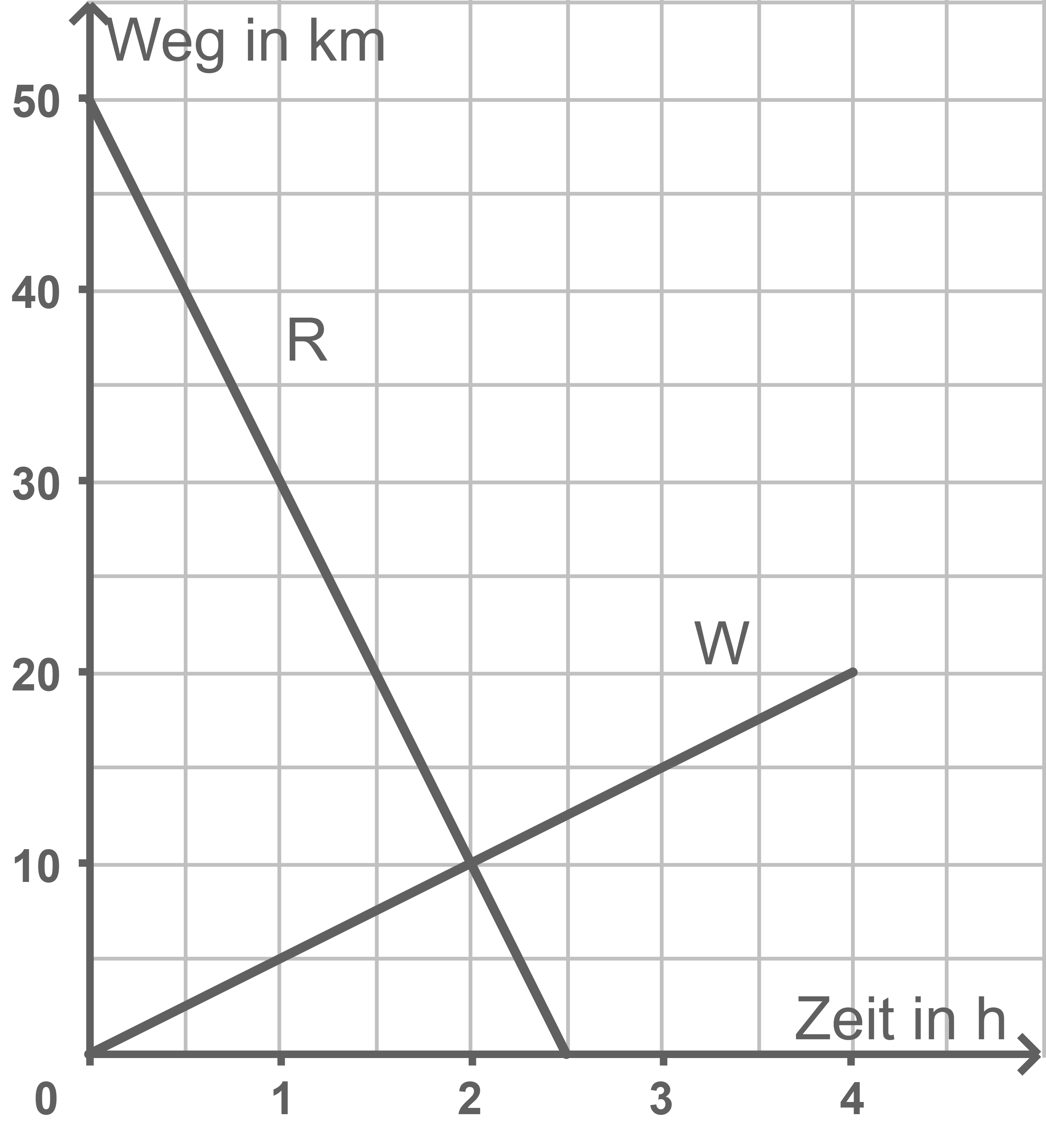
Gib die Aussagen an, die für den dargestellten Sachverhalt zutreffen.
(A) Der Wanderer läuft
in einer Stunde.
(B) Beide treffen sich nach zwei Stunden.
(C) Der Radfahrer fährt
in einer Stunde.
(D) In einer halben Stunde legt der Radfahrer
zurück.
(E) Der Radfahrer und der Wanderer sind beim Start
voneinander entfernt.
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?Kosten morgens:
Kosten abends:
Kosten morgens - Kosten abends:
Karl würde sparen.
Die maximale Strecke, die Karl mit vollem Tank zurücklegen kann, beträgt ca.
Volumen der Regentonne:
bzw.
(Faktor
von
zu
Fläche des Dachs:
Volumen des Regens:
bzw.
da
Nun können wir das Volumen der Tonne und das des Regens vergleichen und merken:
folglich ist die Regentonne groß genug.
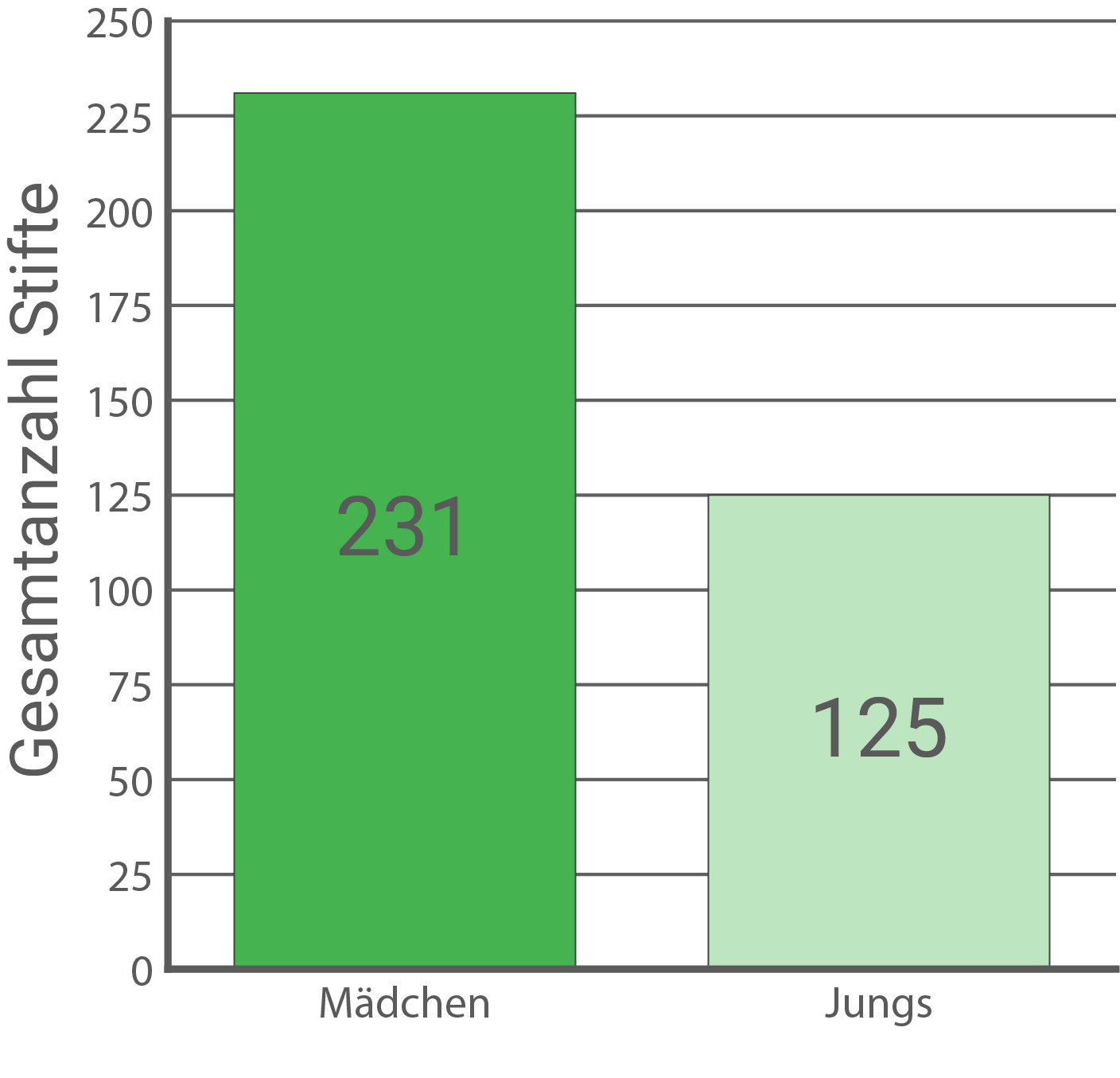
Um die Spannweite für die Anzahl der Farbstifte der Mädchen zu berechnen, muss die minimale Anzahl von der maximalen abgezogen werden:
Die Spannweite der Anzahl der Farbstifte der Mädchen beträgt Farbstifte.
Um das arithmetische Mittel der Anzahl der Farbstifte zu erhalten, muss die Gesamtzahl der Stifte durch die Anzahl der Personen, denen diese gehören, geteilt werden:
Das arithmetische Mittel der Anzahl der Farbstifte der Mädchen beträgt Farbstifte.
Begründung: Max’ Diagramm ist falsch, da er alle Anteile etwa gleich groß dargestellt hat.
Die Wahrscheinlichkeit setzt sich aus der Anzahl gepunkteter Strümpfe geteilt durch die Anzahl aller Strümpfe zusammen.
Also beträgt die Wahrscheinlichkeit, dass Kerstin einen gepunkteten Strumpf aus der Schublade zieht da es
gepunktete Strümpfe und
Strümpfe insgesamt gibt.
Um errechnen zu können, muss zuerst die andere fehlende Seite des kleinen Dreiecks berechnet werden. Hierfür zieht man die Länge der Unterseite des linken Dreiecks von der Gesamtlänge der Unterseite des zusammengesetzten Dreiecks ab:
Satz des Pythagoras anwenden:
Wurzel ziehen, um zu erhalten:
Die Länge der Seite beträgt etwa
Zur Bestimmung des Flächeninhalts des grauen Dreiecks wird der Flächeninhalt des großen Dreiecks berechnet und dann der des kleinen abgezogen. Die Formel lautet Also:
Da dies aber nur den Flächeninhalt des halben Logos ergibt, muss dieser noch verdoppelt werden:
Nun kann der Preis berechnet werden:
für das Gerüst:
Da ist, ist das Angebot B günstiger.
z.B. für
Dies entspricht näherungsweise also kann diese Formel verwendet werden.
Hier setzen:
Da es nicht möglich ist, eine negative Masse zu besitzen, funktioniert die Formel in diesem Ausnahmefall nicht.
Richtige Antworten: