Ableitung
Bei der mittleren Änderungsrate wird die Änderung in einem Intervall berechnet.
 für
für  berechnet. Gibt es einen solchen Grenzwert, dann ist die Funktion differenzierbar.
Dieser Grenzwert wird als Ableitung von
berechnet. Gibt es einen solchen Grenzwert, dann ist die Funktion differenzierbar.
Dieser Grenzwert wird als Ableitung von  an der Stelle
an der Stelle  bezeichnet.
Die Schreibweise für die Ableitung ist:
bezeichnet.
Die Schreibweise für die Ableitung ist: 
 mit der Steigung
mit der Steigung  verläuft, wird Tangente genannt.
verläuft, wird Tangente genannt.
Momenentane Änderungsrate
Wird das Intervall immer weiter verringert, bis es nur noch ein "Punkt" ist, dann spricht man von der momentanen Änderungsrate. Dabei wird der Grenzwert des DifferenzenquotientenTangente
Die Gerade, die durch den Punkt
1
Gegeben ist die Normalparabel  mit
mit 
a)
Ermittle grafisch die Ableitung an der Stelle 
b)
Bestimme rechnerisch die Ableitung an der Stelle  mit dem Grenzwert des Differenzenquotienten.
mit dem Grenzwert des Differenzenquotienten.
c)
Bestimme rechnerisch die Ableitung an der Stelle  mit dem Grenzwert des Differenzenquotienten.
mit dem Grenzwert des Differenzenquotienten.
2
Gegeben ist die Funktion  Bestimme jeweils rechnerisch die Ableitung an der angegeben Stelle.
Bestimme jeweils rechnerisch die Ableitung an der angegeben Stelle.

Ableitung an der Stelle

Ableitung an der Stelle

Ableitung an der Stelle

Ableitung an der Stelle
a)
Ableitung an der Stelle
b)
Ableitung an der Stelle
c)
Ableitung an der Stelle
d)
Ableitung an der Stelle
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
1
a)
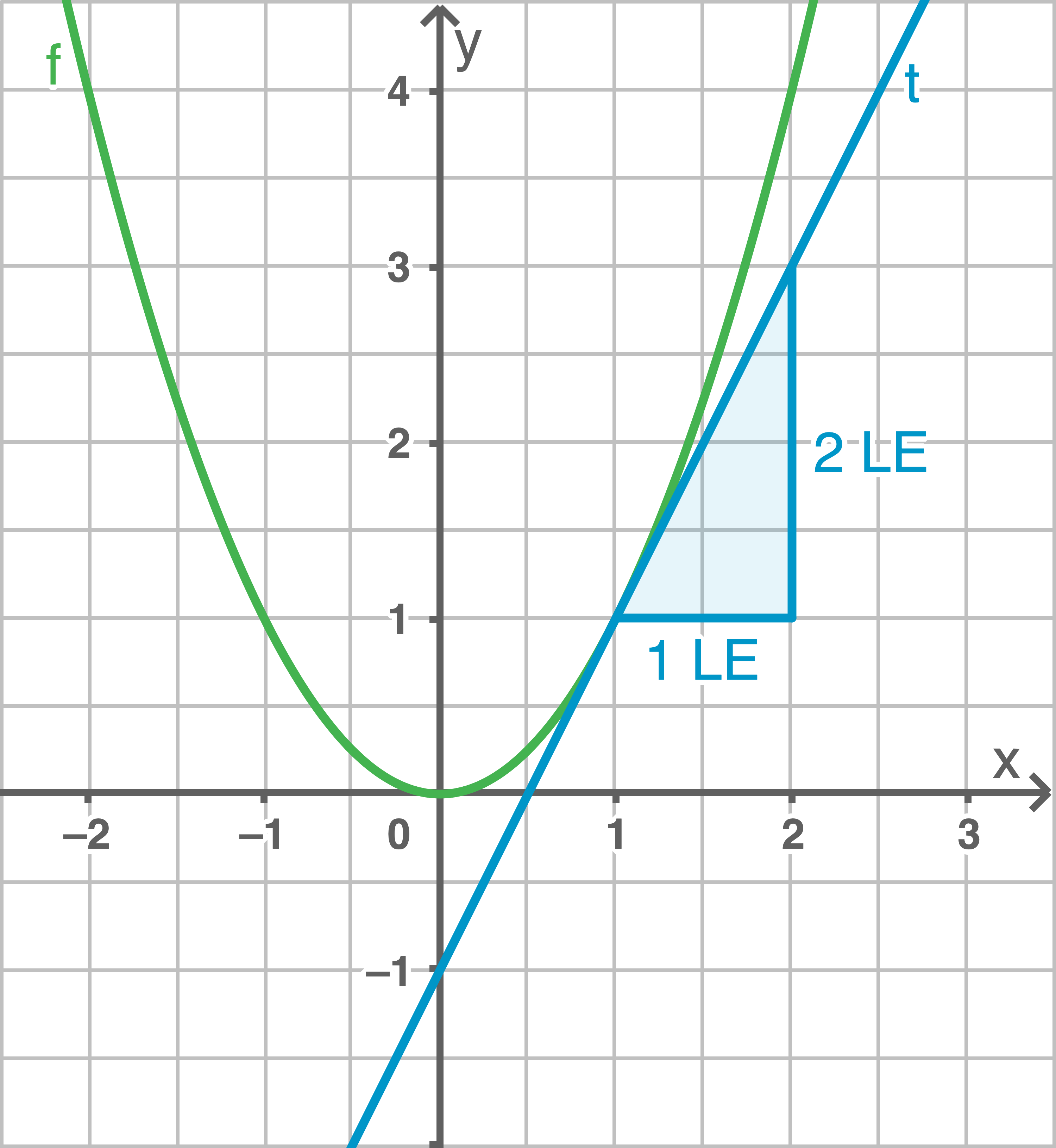
b)
c)
2
a)
b)
c)
d)