Wahlteil B
Aufgabe 1
a)
Gegeben ist die zusammengesetzte Figur (Maße in cm).
- Zeige, dass der Umfang der Figur
beträgt.
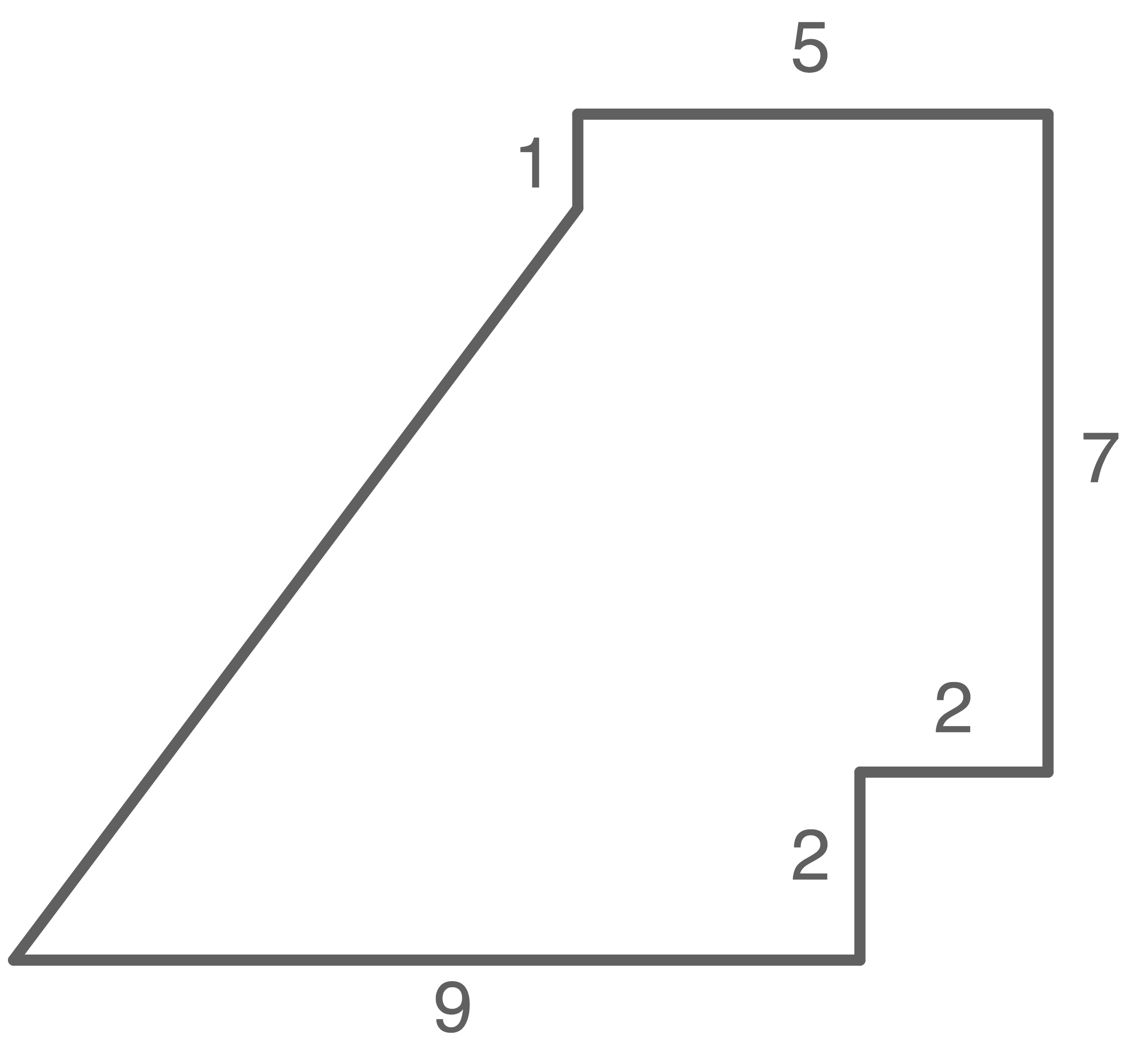
(Skizze nicht maßstabsgetreu)
- Erkläre, wie Ludwig zu diesem Term gekommen ist.
- Veranschauliche deinen Lösungsweg in der Skizze.
- Gib dazu den passenden Term an.

(Skizze nicht maßstabsgetreu)
Term: 
Ein Rechteck hat einen Flächeninhalt von Die Seite
- Bestimme die Seitenlängen
und
des Rechtecks.
(5 Pkt.)
b)
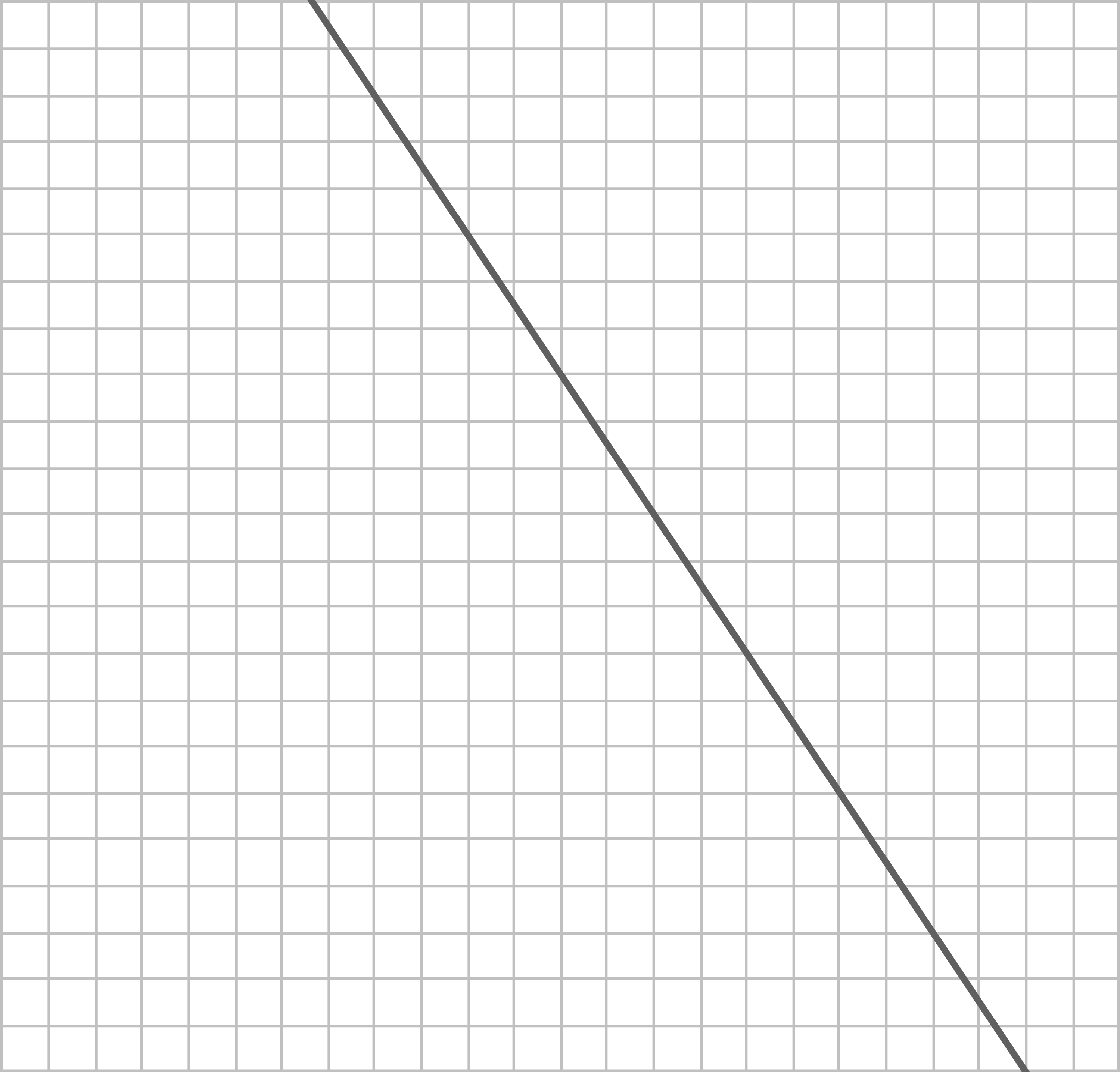
Eine Gerade mit der Funktionsgleichung  wurde gezeichnet.
wurde gezeichnet.
 Leider hat Luca seine Zahlenkombination vergessen.
Leider hat Luca seine Zahlenkombination vergessen.
Er kann sich nur an Folgendes erinnern: - Die Ziffern werden von links nach rechts immer um eins größer. - Die letzte Ziffer ist eine ungerade Zahl.

- Zeichne ein vollständig beschriftetes Koordinatensystem so ein, dass der Graph der Funktionsgleichung korrekt eingetragen ist.
| -3 | -8 |
| -2 | -5 |
| -1 | -2 |
| 0 | 1 |
| 1 | 4 |
| 2 | 7 |
| 3 | 10 |
- Beschreibe anhand der Wertetabelle, wie die Funktionsgleichung dieser linearen Funktion bestimmt werden kann.
Luca hat sich ein Fahrradschloss gekauft. Das Schloss besitzt 4 Einstellringe mit den Ziffern von 0 bis 9. Bei der Zahlenkombination kann jede Ziffer mehrfach vorkommen.
- Berechne die Anzahl aller Kombinationsmöglichkeiten.

Er kann sich nur an Folgendes erinnern: - Die Ziffern werden von links nach rechts immer um eins größer. - Die letzte Ziffer ist eine ungerade Zahl.
- Gib alle Kombinationsmöglichkeiten an.
- Bestimme die prozentuale Wahrscheinlichkeit, dass alle vier Ziffern gleich sind.
(5 Pkt.)
Aufgabe 2
a)
Auf der Oberfläche des quadratischen Prismas mit  und
und  liegt der Streckenzug
liegt der Streckenzug 
- Berechne die Länge des Streckenzuges
- Zeichne das Netz des Prismas und trage den Streckenzug ein.
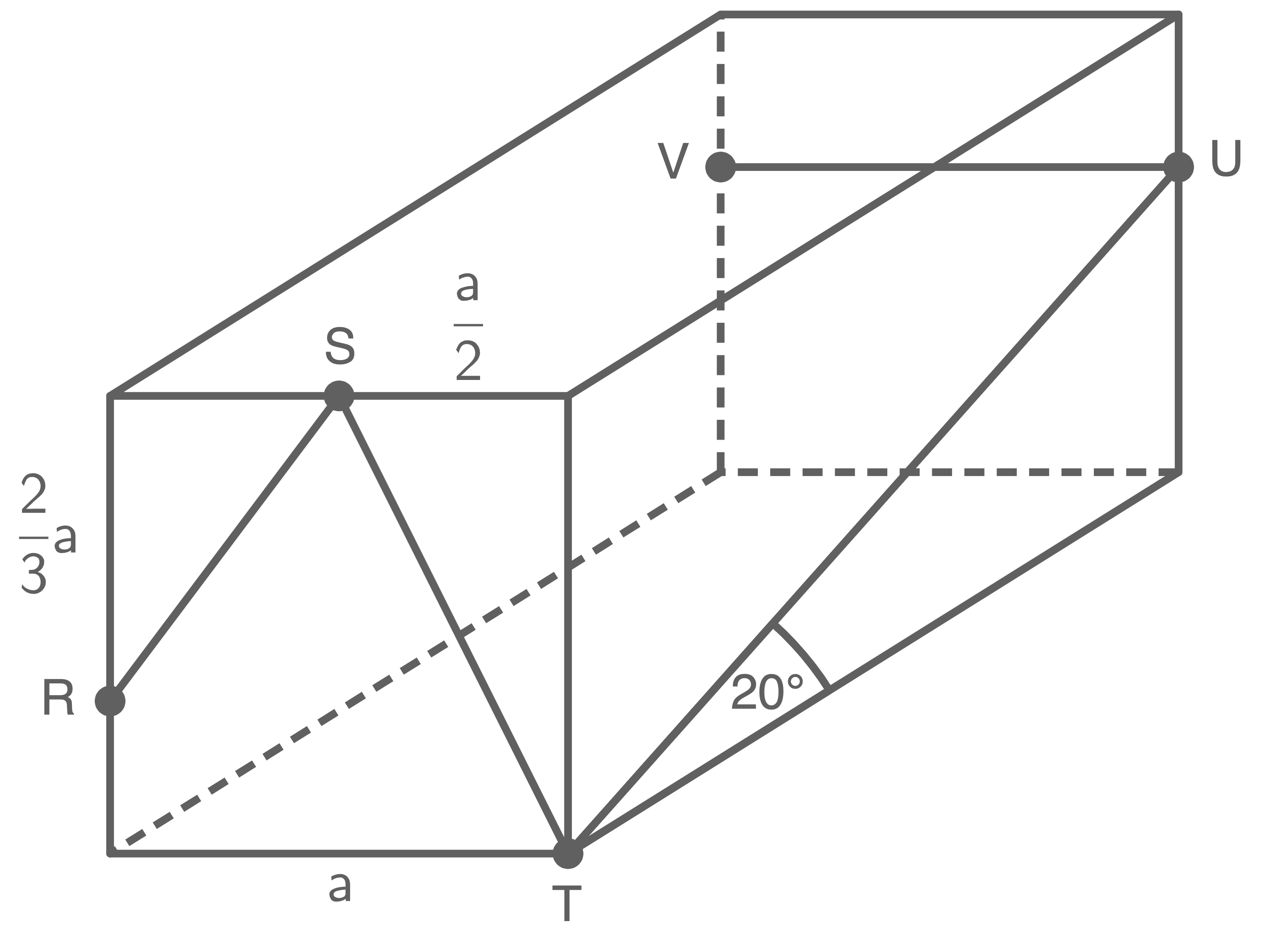
Skizze nicht maßstäblich
- Nimm Stellung und begründe deine Entscheidung.
(5 Pkt.)
b)
Zu einer verschobenen, nach unten geöffneten Normalparabel gehört folgende Wertetabelle:
 besitzt nur negative
besitzt nur negative  -Werte“. Hat Till Recht?
-Werte“. Hat Till Recht?

| -3 | -10 |
| -2 | |
| -1 | |
| 0 | |
| 1 | |
| 2 | -5 |
| 3 | -10 |
- Bestimme die Funktionsgleichung der Parabel.
- Vervollständige die Wertetabelle.
- Begründe deine Entscheidung durch Argumentation.
- Löse die Gleichung.
(5 Pkt.)
Aufgabe 3
a)
In einen Kreis mit dem Radius  wurde der Mantel einer quadratischen Pyramide eingezeichnet.
wurde der Mantel einer quadratischen Pyramide eingezeichnet.
- Berechne die Oberfläche der Pyramide.
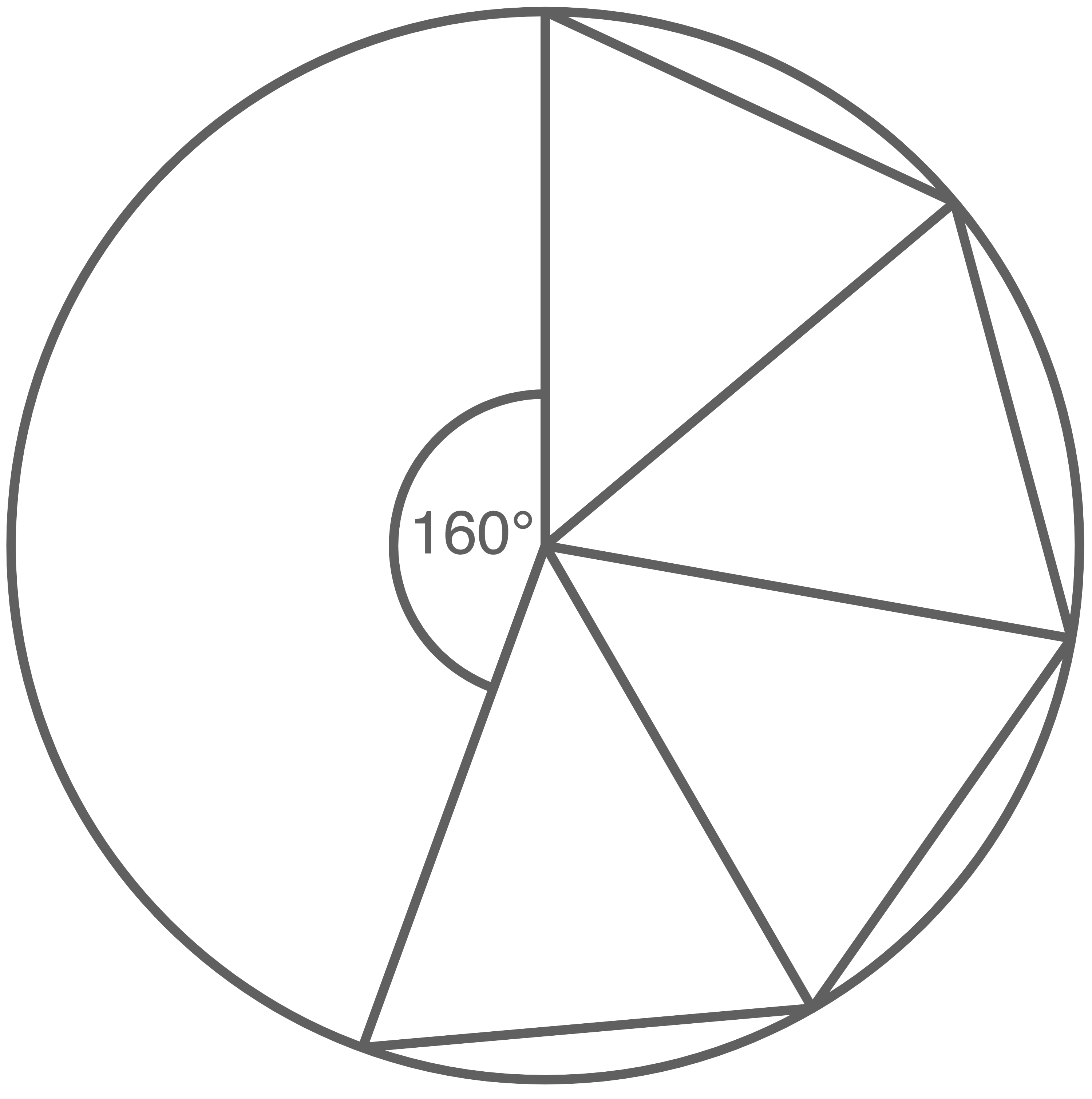
(Skizze nicht maßstabsgetreu)
(Skizze nicht maßstabsgetreu)
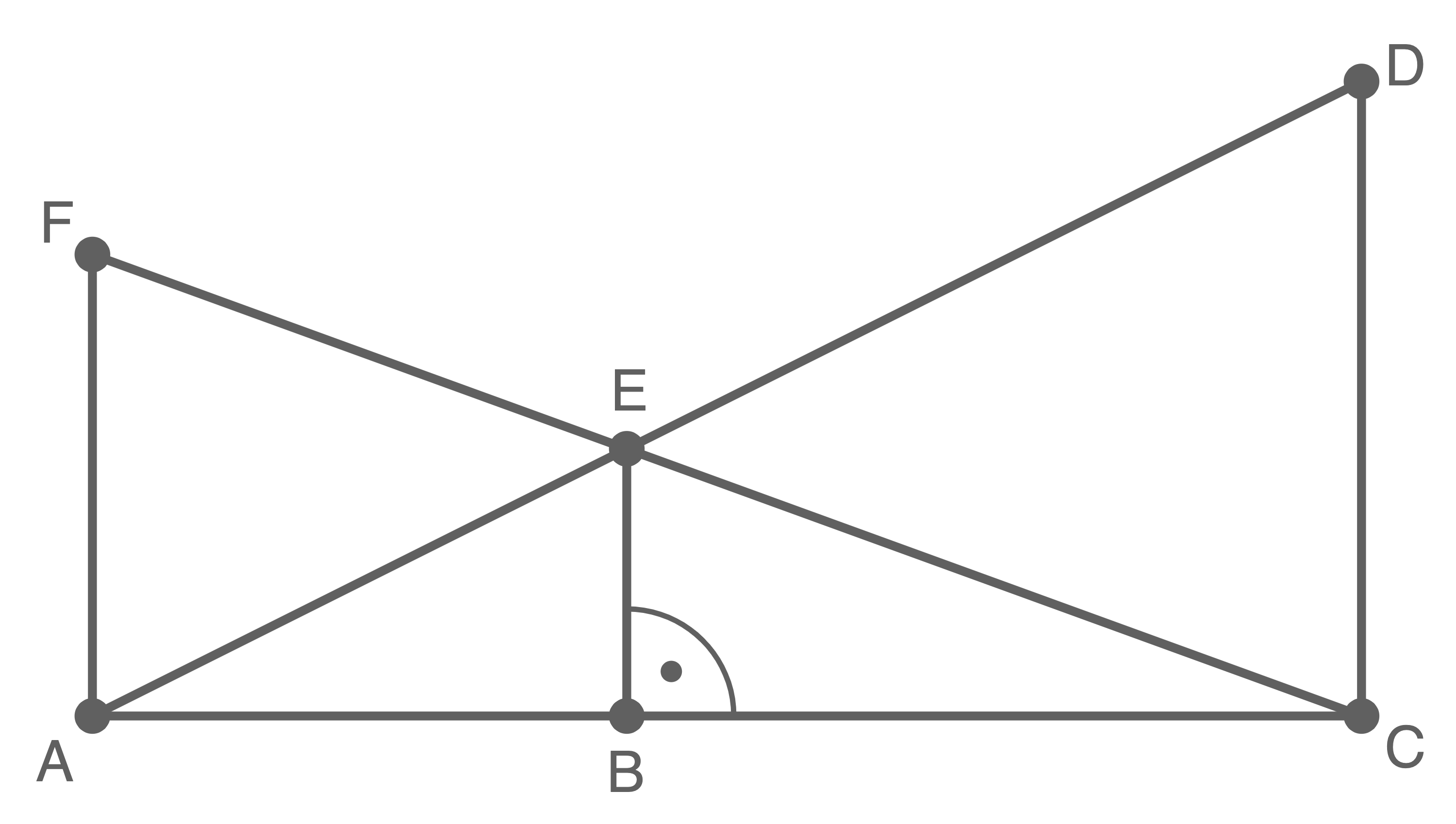
- Kreuze die richtigen Verhältnisgleichungen an.
- Stelle eine Verhältnisgleichung zur Berechnung von
auf.
Verwende hierzu den 2. Strahlensatz.
(5 Pkt.)
b)
Frau Steiner möchte sich ein neues E-Bike für  kaufen.
Ein Fahrradhändler wirbt mit folgender Rabattaktion:
kaufen.
Ein Fahrradhändler wirbt mit folgender Rabattaktion:
 Rabatt bei Kauf eines E-Bikes!!!
Bei Barzahlung gibt es nochmals
Rabatt bei Kauf eines E-Bikes!!!
Bei Barzahlung gibt es nochmals  Skonto.
Frau Steiner rechnet aus, wie viel sie nun für das E-Bike bezahlen muss:
Skonto.
Frau Steiner rechnet aus, wie viel sie nun für das E-Bike bezahlen muss:
![\(\begin{array}[t]{rll}
100\,\%&\mathrel{\widehat{=}}& 5\,200\,\text € & \\[5pt]
1\,\%&\mathrel{\widehat{=}}& 52\,\text € & \\[5pt]
17\,\%&\mathrel{\widehat{=}}& 884\,\text € \\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/a0f6317e67c5ff562eb3e6d82e6df0dd736607c06370891f418586b3e3f4a5b2_light.svg)


Die Höhe des Kegels ist genauso groß wie der Durchmesser der Kugel.
Der Kegel und die Kugel haben das gleiche Volumen.
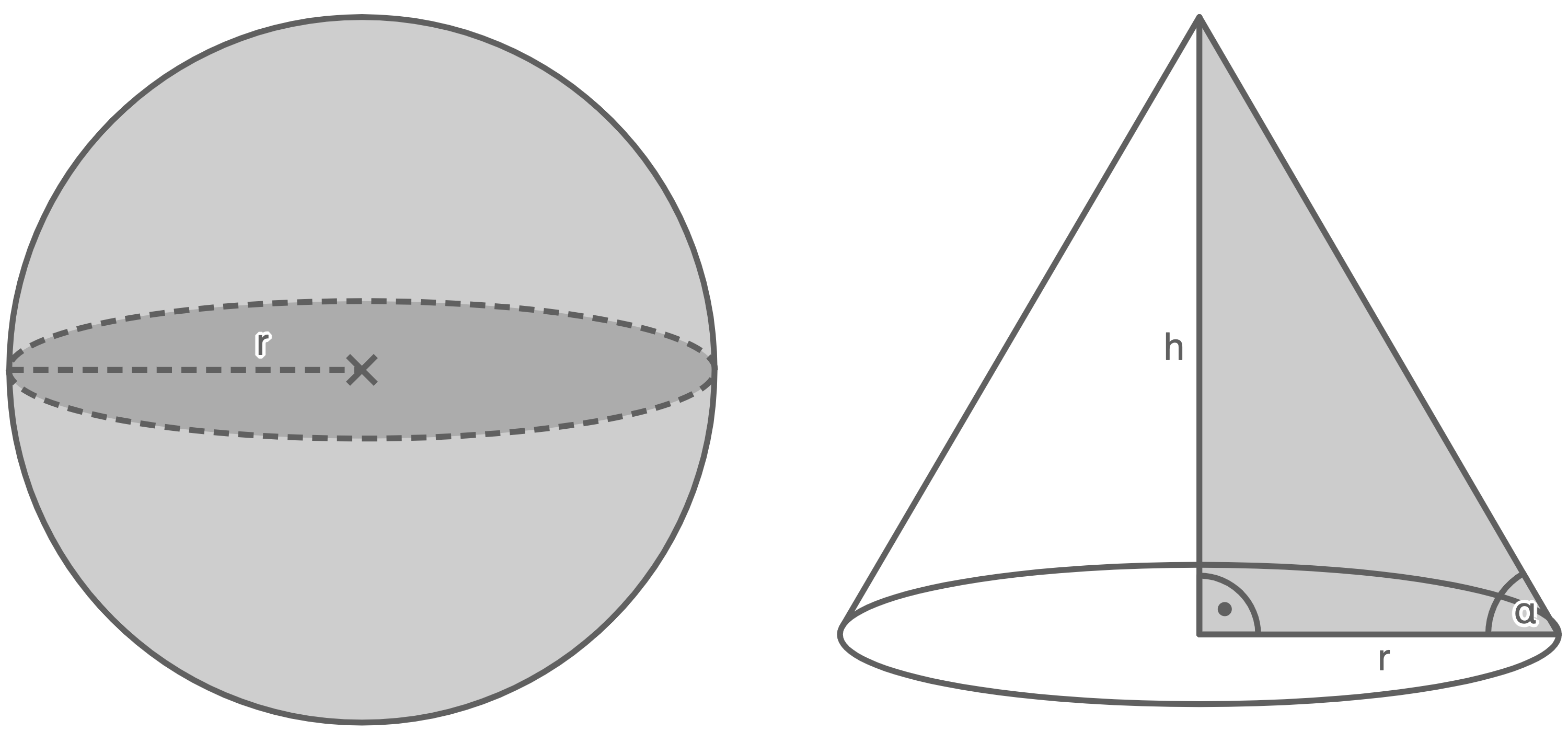
Wie verändert sich das Volumen des Kegels, wenn die Höhe gleich bleibt?
- Beschreibe und erkläre, was Frau Steiner falsch gemacht hat.
- Berechne den Kaufpreis des E-Bikes nach dem Angebot des Fahrradhändlers.
Die Höhe des Kegels ist genauso groß wie der Durchmesser der Kugel.
Der Kegel und die Kugel haben das gleiche Volumen.

(Skizzen nicht maßstabsgetreu)
- Bestimme den Neigungswinkel
des Kegels.
Wie verändert sich das Volumen des Kegels, wenn die Höhe gleich bleibt?
- Kreuze an.
Das Volumen des Kegels bleibt gleich. Das Volumen des Kegels vergrößert sich. Das Volumen des Kegels verkleinert sich.
(5 Pkt.)
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?Lösung 1
a)
Umfang berechnen
Mit dem Satz des Pythagoras kann die Länge  der fehlenden Strecke berechnet werden:
Für den Umfang des Trapezes folgt:
Term erklären
Die Figur wurde in die folgenden Teilflächen zerlegt:
der fehlenden Strecke berechnet werden:
Für den Umfang des Trapezes folgt:
Term erklären
Die Figur wurde in die folgenden Teilflächen zerlegt:
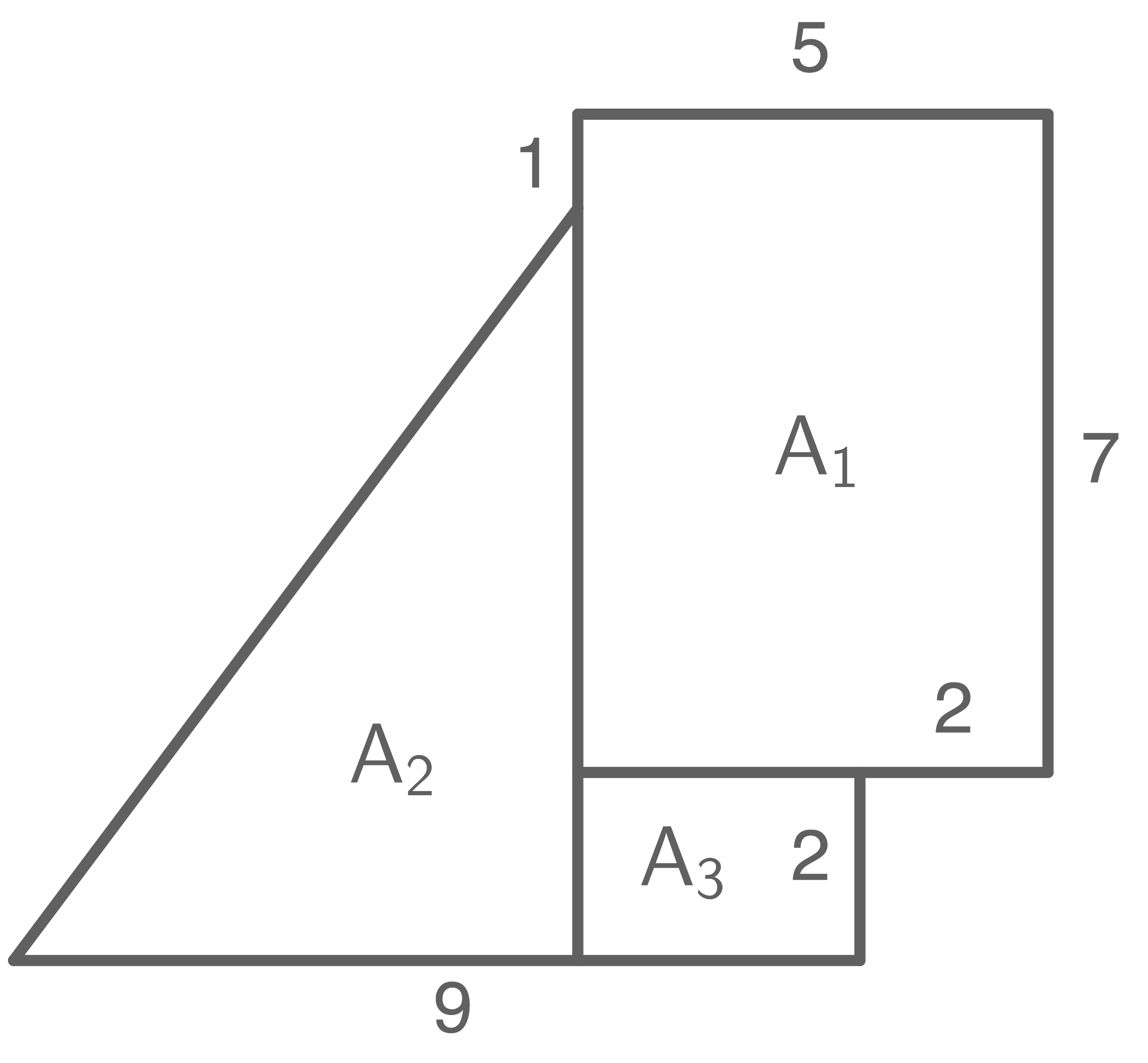 Mit dem Term
Mit dem Term  wird der Flächeninhalt
wird der Flächeninhalt  des Rechtecks berechnet.
Mit dem Term
des Rechtecks berechnet.
Mit dem Term  wird der Flächeninhalt
wird der Flächeninhalt  des Dreiecks berechnet.
Mit dem Term
des Dreiecks berechnet.
Mit dem Term  wird der Flächeninhalt
wird der Flächeninhalt  des Rechtecks berechnet.
Lösungsweg veranschaulichen und Term angeben
des Rechtecks berechnet.
Lösungsweg veranschaulichen und Term angeben
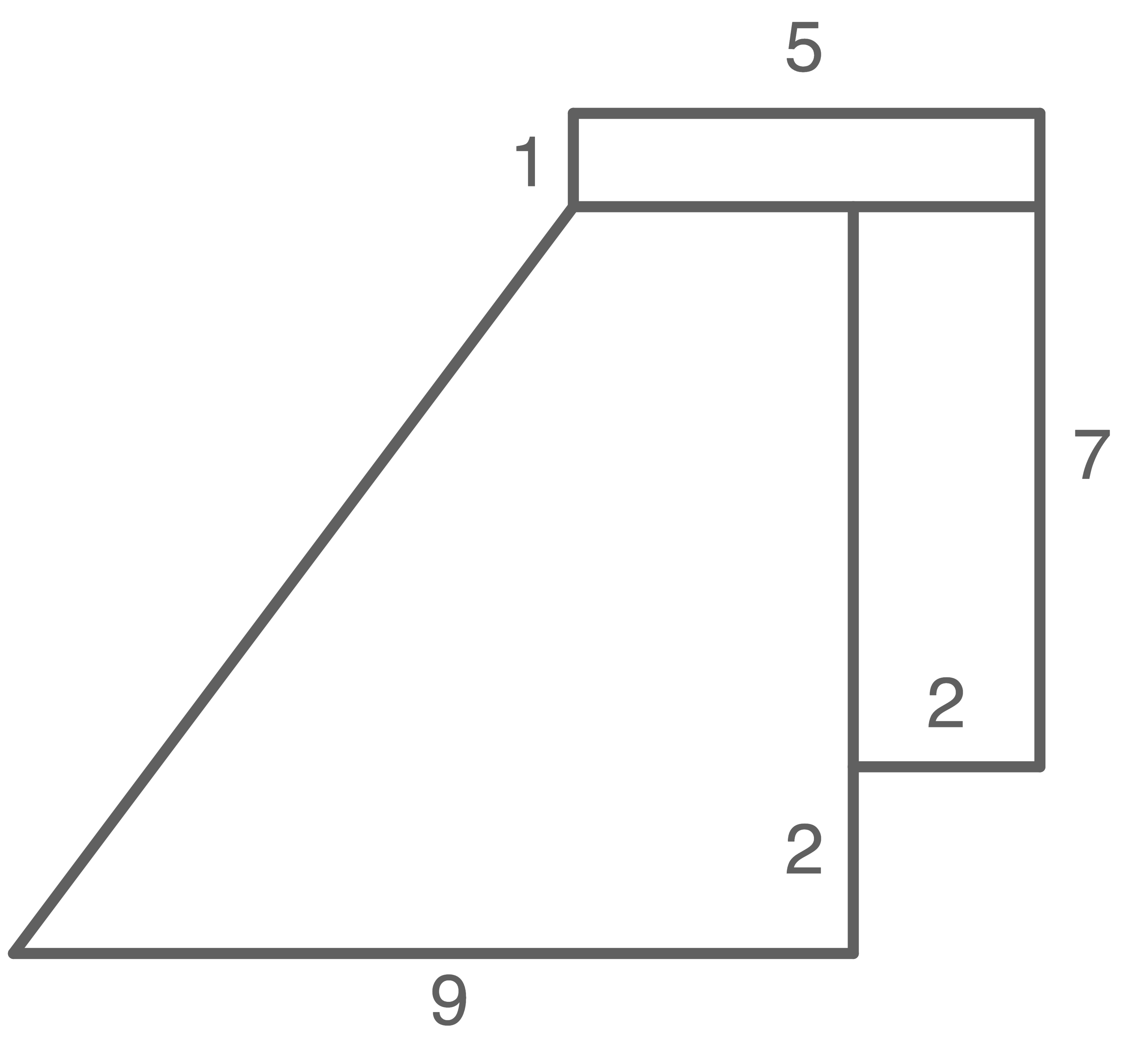
![\(\begin{array}[t]{rll}
a\cdot b&=& 108 \\[5pt]
3b\cdot b&=& 108 \\[5pt]
3b^2&=& 108 \quad \scriptsize \mid\; :3 \\[5pt]
b^2&=& 36 \quad \scriptsize \mid\; \sqrt{\,} \\[5pt]
b&=& 6
\end{array}\)](https://www.schullv.de/resources/formulas/bc4a795822d4b46756ac5927dfaae4c77167656bb643f1b8fc63c082c5e6d032_light.svg) Daraus folgt
Daraus folgt  Das Rechteck hat die Seitenlängen
Das Rechteck hat die Seitenlängen  und
und 


Term: 
Seitenlängen des Rechtecks bestimmen
Es muss gelten:
b)
Koordinatensystem einzeichnen
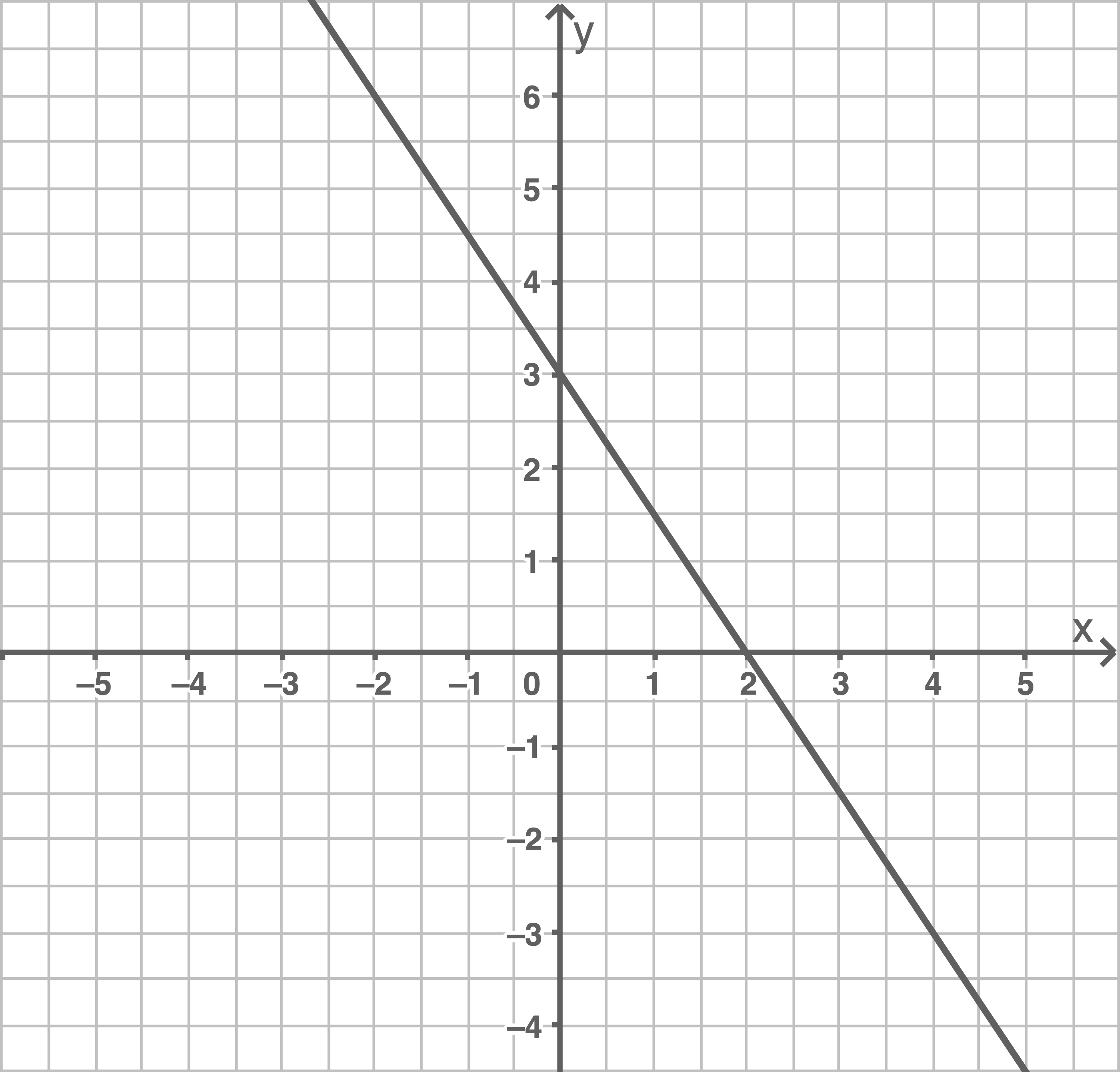 Beschreiben, wie Funktionsgleichung bestimmt werden kann
Der
Beschreiben, wie Funktionsgleichung bestimmt werden kann
Der  -Achsenabschnitt
-Achsenabschnitt  ist gegeben durch den
ist gegeben durch den  -Wert an der Stelle
-Wert an der Stelle  also
also  Die Steigung
Die Steigung  lässt sich berechnen, indem die Differenz der
lässt sich berechnen, indem die Differenz der  -Werte bei einem Schritt entlang der
-Werte bei einem Schritt entlang der  -Achse berechnet wird:
-Achse berechnet wird:
 Insgesamt gilt also
Insgesamt gilt also  Anzahl Kombinationsmöglichkeiten berechnen
Es gibt
Anzahl Kombinationsmöglichkeiten berechnen
Es gibt  Kombinationsmöglichkeiten.
Kombinationsmöglichkeiten angeben
Kombinationsmöglichkeiten.
Kombinationsmöglichkeiten angeben
 Wahrscheinlichkeit für vier gleiche Ziffern angeben
Es gibt insgesamt
Wahrscheinlichkeit für vier gleiche Ziffern angeben
Es gibt insgesamt  Kombinationsmöglichkeiten und
Kombinationsmöglichkeiten und  mögliche Kombinationen mit 4 gleichen Ziffern.
mögliche Kombinationen mit 4 gleichen Ziffern.


Lösung 2
a)
Länge des Streckenzugs berechnen
![\(\begin{array}[t]{rll}
\overline{RS}^2&=& \left(\dfrac{2}{3}\cdot 3\right)^2+\left(\dfrac{3}{2}\right)^2 \quad \scriptsize \mid\; \sqrt{\,} \\[5pt]
\overline{RS}&=& \sqrt{\left(\dfrac{2}{3}\cdot 3\right)^2+\left(\dfrac{3}{2}\right)^2} \\[5pt]
\overline{RS}&=& 2,5
\end{array}\)](https://www.schullv.de/resources/formulas/c98e7d79730dc83be0ac819be69ffbfb973f80682edce8681365769a0dd89342_light.svg)
![\(\begin{array}[t]{rll}
\overline{ST}^2&=& \left(\dfrac{3}{2}\right)^2+3^2 \quad \scriptsize \mid\; \sqrt{\,} \\[5pt]
\overline{ST}&=& \sqrt{\left(\dfrac{3}{2}\right)^2+3^2} \\[5pt]
\overline{ST}&=& 3,35
\end{array}\)](https://www.schullv.de/resources/formulas/bf2096bb0ab4fbf936b2445074a8e61c4f0f6c50e0903caf7bb30fa268075e73_light.svg)
![\(\begin{array}[t]{rll}
\cos(20°)&=& \dfrac{2\cdot 3}{\overline{TU}} \quad \scriptsize \mid\; \cdot \overline{TU} \\[5pt]
\cos(20°)\cdot \overline{TU}&=& 6 \quad \scriptsize \mid\; :\cos(20°) \\[5pt]
\overline{TU}&=& \dfrac{6}{\cos(20°)} \\[5pt]
\overline{TU}&=& 6,39
\end{array}\)](https://www.schullv.de/resources/formulas/d3a806067cd64bc0daf4a2f8efa736db92b08f6d9c8571907987f9e7e5a11e8e_light.svg)
 Insgesamt ergibt sich damit die Länge des Streckenzugs:
Insgesamt ergibt sich damit die Länge des Streckenzugs:
![\(2,5+3,35+6,39+3=15,24\,\text{[cm]}\)](https://www.schullv.de/resources/formulas/4c10c87727d29bd3792a2b4e0db4074eb2e21491c5ce5db5343dadf271e8402d_light.svg) Netz mit Streckenzug zeichnen
Netz mit Streckenzug zeichnen
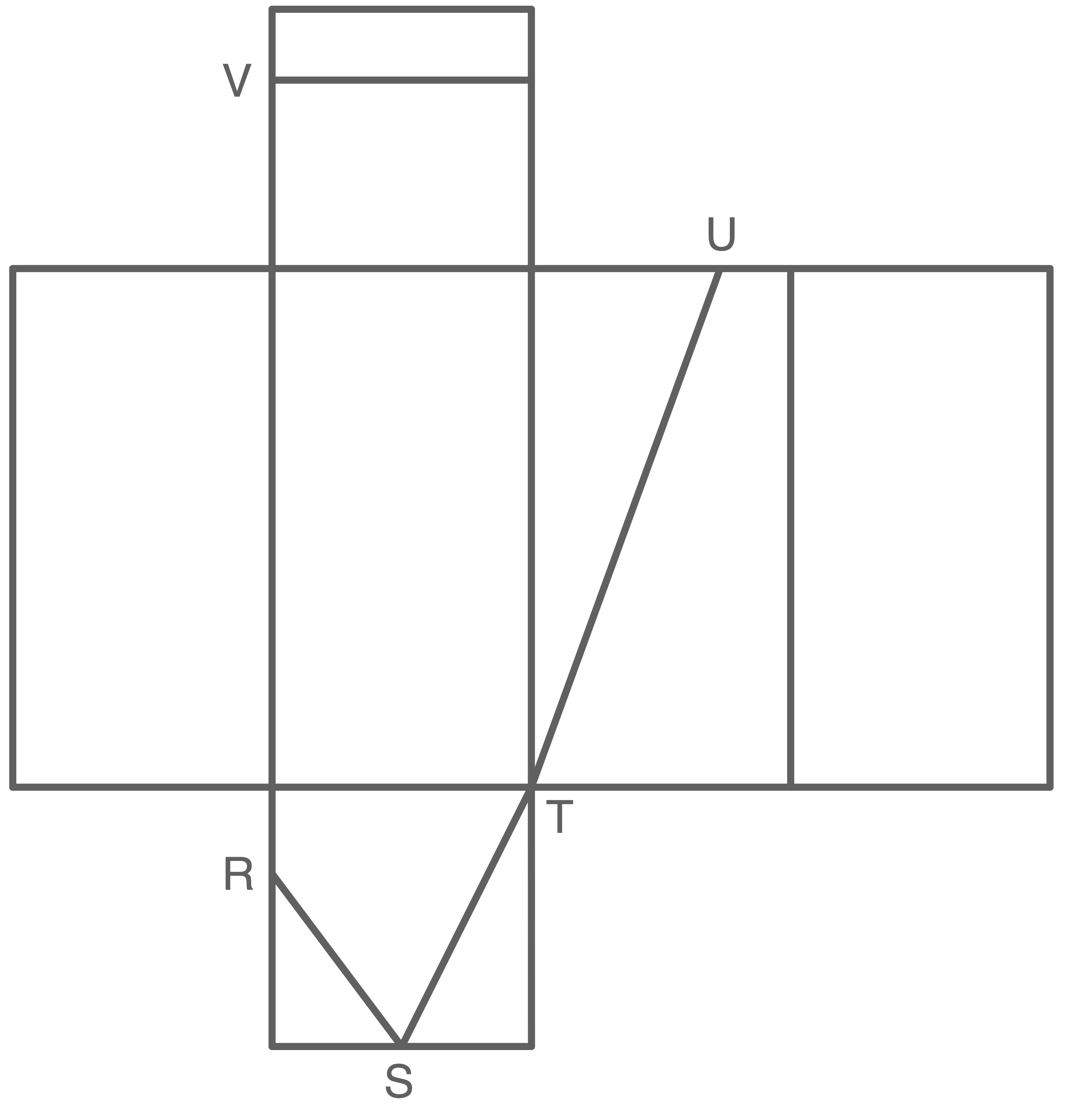 Behauptung überprüfen
Emils Behauptung ist falsch. Bei einer Verdopplung der Seitenlängen der Grundfläche vervierfacht sich das Volumen
Behauptung überprüfen
Emils Behauptung ist falsch. Bei einer Verdopplung der Seitenlängen der Grundfläche vervierfacht sich das Volumen  des Prismas:
des Prismas:


b)
Funktionsgleichung bestimmen
Es handelt sich um eine nach unten geöffnete Parabel der Form  Einsetzen der Koordinaten des Punktes
Einsetzen der Koordinaten des Punktes  liefert:
liefert:
![\(\begin{array}[t]{rll}
-10&=& -3^2+c \\[5pt]
-10&=& -9+c \quad \scriptsize \mid\; +9 \\[5pt]
-1&=& c
\end{array}\)](https://www.schullv.de/resources/formulas/729a49979faca221b902fff8c3c6b6c4fa414f2a46991683b4c0c7ae15418bb0_light.svg) Die Parabel hat die Funktionsgleichung
Die Parabel hat die Funktionsgleichung  Wertetabelle vervollständigen
Wertetabelle vervollständigen
Behauptung überprüfen
Till hat nicht Recht.
Liegt der Scheitelpunkt bei einer solchen Normalparabel oberhalb der  -Achse, gilt also
-Achse, gilt also  so besitzt die Parabel auch positive
so besitzt die Parabel auch positive  -Werte.
Gleichung lösen
Das Produkt der beiden Terme ist gleich null, wenn einer der beiden Faktoren gleich null ist.
-Werte.
Gleichung lösen
Das Produkt der beiden Terme ist gleich null, wenn einer der beiden Faktoren gleich null ist.
![\(\begin{array}[t]{rll}
3x+6&=& 0 \quad \scriptsize \mid\; -6\\[5pt]
3x&=& -6 \quad \scriptsize \mid\; :3 \\[5pt]
x_1&=& -2
\end{array}\)](https://www.schullv.de/resources/formulas/50d351edcb47e690ec04004fd943f47ef696b7721913a9017d7851a2d5f84898_light.svg)
![\(\begin{array}[t]{rll}
4-2x&=& 0 \quad \scriptsize \mid\; -4 \\[5pt]
-2x&=& -4 \quad \scriptsize \mid\; :(-2) \\[5pt]
x_2&=& 2
\end{array}\)](https://www.schullv.de/resources/formulas/2c4cc9155cd33f3b521af69389f88c0d99bacc257c53fde1be7ce45d92eec7be_light.svg)

| -3 | -10 |
| -2 | -5 |
| -1 | -2 |
| 0 | -1 |
| 1 | -2 |
| 2 | -5 |
| 3 | -10 |
Lösung 3
a)
Oberfläche der Pyramide berechnen
Winkel  an der Spitze einer dreieckigen Seitenfläche berechnen:
an der Spitze einer dreieckigen Seitenfläche berechnen:
 Länge der Grundseite
Länge der Grundseite  einer dreieckigen Seitenfläche mit dem Kosinussatz berechnen:
einer dreieckigen Seitenfläche mit dem Kosinussatz berechnen:
![\(\begin{array}[t]{rll}
a^2&=& 8^2+8^2-2\cdot 8\cdot 8\cdot \cos(50°) \quad \scriptsize \mid\; \sqrt{\,} \\[5pt]
a&=& \sqrt{8^2+8^2-2\cdot 8\cdot 8\cdot \cos(50°)} \\[5pt]
a&=& 6,76\,\text{[cm]}
\end{array}\)](https://www.schullv.de/resources/formulas/e8712cbc061600c6ab89361fc21aed4419698145ef729b936ba77d7ebe8cc5ee_light.svg) Für die Höhe
Für die Höhe  einer dreieckigen Seitenfläche gilt mit dem Satz des Pythagoras:
einer dreieckigen Seitenfläche gilt mit dem Satz des Pythagoras:
![\(\begin{array}[t]{rll}
h_s^2+\left(\dfrac{a}{2}\right)^2&=& r^2 \\[5pt]
h_s^2+\left(\dfrac{6,76}{2}\right)^2&=& 8^2 \quad \scriptsize \mid\; -\left(\dfrac{6,76}{2}\right)^2 \\[5pt]
h_s^2&=& 8^2-\left(\dfrac{6,76}{2}\right)^2 \quad \scriptsize \mid\; \sqrt{\,} \\[5pt]
h_s&=& \sqrt{8^2-\left(\dfrac{6,76}{2}\right)^2} \\[5pt]
h_s&=& 7,25\,\text{[cm]}
\end{array}\)](https://www.schullv.de/resources/formulas/62e1e5f0dd07b82efd028cb60a7aa4c3e4e7a30c26fd3811abce559436b25eba_light.svg) Damit lässt sich schließlich die Oberfläche der Pyramide berechnen:
Damit lässt sich schließlich die Oberfläche der Pyramide berechnen:
![\(\begin{array}[t]{rll}
O&=& 4\cdot \dfrac{1}{2}\cdot a\cdot h_s+a^2 \\[5pt]
&=& 4\cdot \dfrac{1}{2}\cdot 6,76\cdot 7,25+6,76^2 \\[5pt]
&=& 143,72\,[\text{cm}^2]
\end{array}\)](https://www.schullv.de/resources/formulas/ee2d56fb67136eab5100f52b264f62790fb03e33e3813e04364af00d4a31ac8b_light.svg) Richtige Verhältnisgleichungen ankreuzen
Richtige Verhältnisgleichungen ankreuzen
Verhältnisgleichung aufstellen
Es gibt viele verschiedene Möglichkeiten, zum Beispiel 
b)
Erklären, was Frau Steiner falsch gemacht hat
Frau Steiner hat beide Rabatte vom selben Grundwert abgezogen.
Der Grundwert vermindert sich jedoch nach der ersten Preissenkung. Der zweite Rabatt muss daher vom neuen Grundwert abgezogen werden.
Kaufpreis berechnen




![\(\begin{array}{rcl}
100\,\% & \mathrel{\widehat{=}}& 5\,200\,\text €\\[5pt]
1\,\% & \mathrel{\widehat{=}}& 52\,\text €\\[5pt]
15\,\% & \mathrel{\widehat{=}}& 780\,\text €
\end{array}\)](https://www.schullv.de/resources/formulas/cf3e7a96d1fe7a72645ddac6d7b2195b7192d1c35050c5a854d894eca939262a_light.svg)



 Kaufpreis nach
Kaufpreis nach  Rabatt:
Rabatt:





![\(\begin{array}{rcl}
100\,\% & \mathrel{\widehat{=}}& 4\,420\,\text €\\[5pt]
1\,\% & \mathrel{\widehat{=}}& 44,20\,\text €\\[5pt]
2\,\% & \mathrel{\widehat{=}}& 88,40\,\text €
\end{array}\)](https://www.schullv.de/resources/formulas/787150c345e8eb47b775e4cd686ae04291c9c654c517b01dc39f9bec371be3d0_light.svg)



 Kaufpreis nach weiteren
Kaufpreis nach weiteren  Rabatt:
Rabatt:
 Neigungswinkel des Kegels berechnen
Volumen der Kugel berechnen:
Neigungswinkel des Kegels berechnen
Volumen der Kugel berechnen:
![\(\begin{array}[t]{rll}
V_\text{Kugel}&=& \dfrac{4}{3}\cdot \pi\cdot (25\,\text{cm})^3 \\[5pt]
&=& 65\,449,85\,\text{cm}^3
\end{array}\)](https://www.schullv.de/resources/formulas/98ca68def3987610edfae4b0812fc75108851ce3f6b81969b3f68810a2723bf0_light.svg) Da das Volumen der Kugel so groß ist wie das des Kegels, lässt sich damit der Radius des Kegels berechnen:
Da das Volumen der Kugel so groß ist wie das des Kegels, lässt sich damit der Radius des Kegels berechnen:
![\(\begin{array}[t]{rll}
65\,449,85\,\text{cm}^3&=& \dfrac{1}{3}\cdot \pi\cdot r^2 \cdot 2\cdot 25\,\text{cm} \\[5pt]
65\,449,85\,\text{cm}^3&=& 52,36\,\text{cm} \cdot r^2 \quad \scriptsize \mid\; :52,36\,\text{cm} \\[5pt]
1\,250,95\,\text{cm}^2&=& r^2 \quad \scriptsize \mid\; \sqrt{\,} \\[5pt]
35,37\,\text{cm}&=& r_\text{Kegel}
\end{array}\)](https://www.schullv.de/resources/formulas/33710224893f63b9c0436fe999748d7088f9a6f2ae497fac7df7ae5426c33cf8_light.svg) Damit lässt sich der Winkel
Damit lässt sich der Winkel  mit dem Tangens berechnen:
mit dem Tangens berechnen:
![\(\begin{array}[t]{rll}
\tan(\alpha)&=& \dfrac{h}{r_\text{Kegel}} \\[5pt]
\tan(\alpha)&=& \dfrac{50\,\text{cm}}{35,37\,\text{cm}} \quad \scriptsize \mid\; \tan^{-1} \\[5pt]
\alpha&=& 54,75°
\end{array}\)](https://www.schullv.de/resources/formulas/0efee5c37a5f3d8e2d93cce88612211d5a1b9708253cf52dbe235afd2ff0b994_light.svg) Ankreuzen, wie sich Volumen verändert
Ankreuzen, wie sich Volumen verändert
| Das Volumen des Kegels bleibt gleich. | |
| Das Volumen des Kegels vergrößert sich. | |
| Das Volumen des Kegels verkleinert sich. |