Wahlaufgaben
Wahlaufgabe 1
a)
Das Zelt hat etwa die Form einer Halbkugel.
.png)
.png)
- Berechne die Bodenfläche im Zelt möglichst genau.
- Wie viele Quadratmeter hat die vollständig geschlossene Hülle?
(2 Pkt.)
b)
Laura möchte sich einen neuen Computer kaufen. Dieser kostet 
Sie hat gespart. Für den Rest muss sie einen Ratenkredit aufnehmen.
gespart. Für den Rest muss sie einen Ratenkredit aufnehmen.
Die Bank macht ihr ein Angebot: Zinssatz p.a.
p.a.
Sie hat
Die Bank macht ihr ein Angebot: Zinssatz
- Wie hoch ist ihre Restschuld nach fünf Monaten, wenn sie eine monatliche Rate in Höhe von
bezahlt?
Wie viel Euro Zinsen hat sie bis zu diesem Zeitpunkt bezahlt? - Stelle den Verlauf der Restschuld für jeden Monat in einem aussagekräftigen Diagramm dar.
(2 Pkt.)
c)
Das Koordinatensystem zeigt fünf Parabeln.
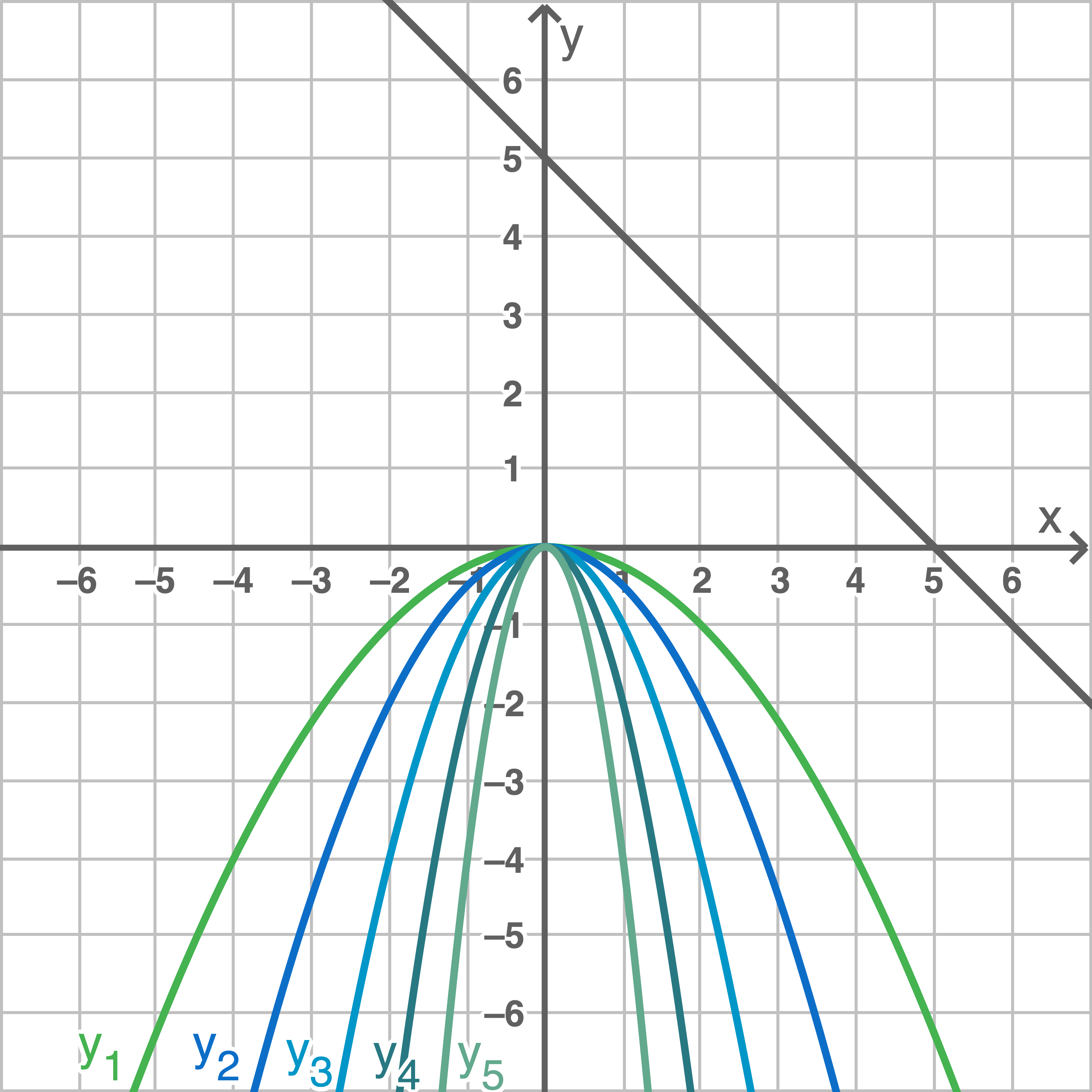

- Gib zu zwei dieser Parabeln die dazugehörige Gleichung an.
- Berechne die Schnittpunkte einer neuen Parabel
mit der eingezeichneten Geraden.
(2 Pkt.)
Wahlaufgabe 2
a)
Florian hält diese sieben Karten (siehe Abbildung) der gleichen Farbe in der Hand.


- Wie viele Möglichkeiten mit zwei Karten gibt es, damit jeweils eine unterschiedliche Zahlenkombination entsteht?
Die Reihenfolge spielt dabei keine Rolle. Gib diese Kombinationsmöglichkeiten an.
- Ermittle, mit welcher Wahrscheinlichkeit genau die Summe
gezogen wird.
Die Reihenfolge muss beachtet werden.
(2 Pkt.)
b)
Direkt nach dem Melken enthält ein Liter Milch durchschnittlich  Keime.
Keime.
Wird die Milch nach dem Melken nicht gekühlt, verdoppelt sich die Anzahl der Keime stündlich.
Ein Liter gekühlte Milch enthält nach fünf Stunden nur Keime.
Keime.
Wird die Milch nach dem Melken nicht gekühlt, verdoppelt sich die Anzahl der Keime stündlich.
- Wie viele Keime enthält ein Liter ungekühlte Milch nach fünf Stunden?
Ein Liter gekühlte Milch enthält nach fünf Stunden nur
- Bestimme die Wachstumsrate der Keime.
Wachstumsrate
=
Prozentsatz des Wachstums
=
Prozentsatz des Wachstums
(2 Pkt.)
c)
Wird an diesem Rechteck die kurze Seite um  und die lange Seite um
und die lange Seite um  verlängert, so beträgt der Umfang des neuen Rechtecks
verlängert, so beträgt der Umfang des neuen Rechtecks 
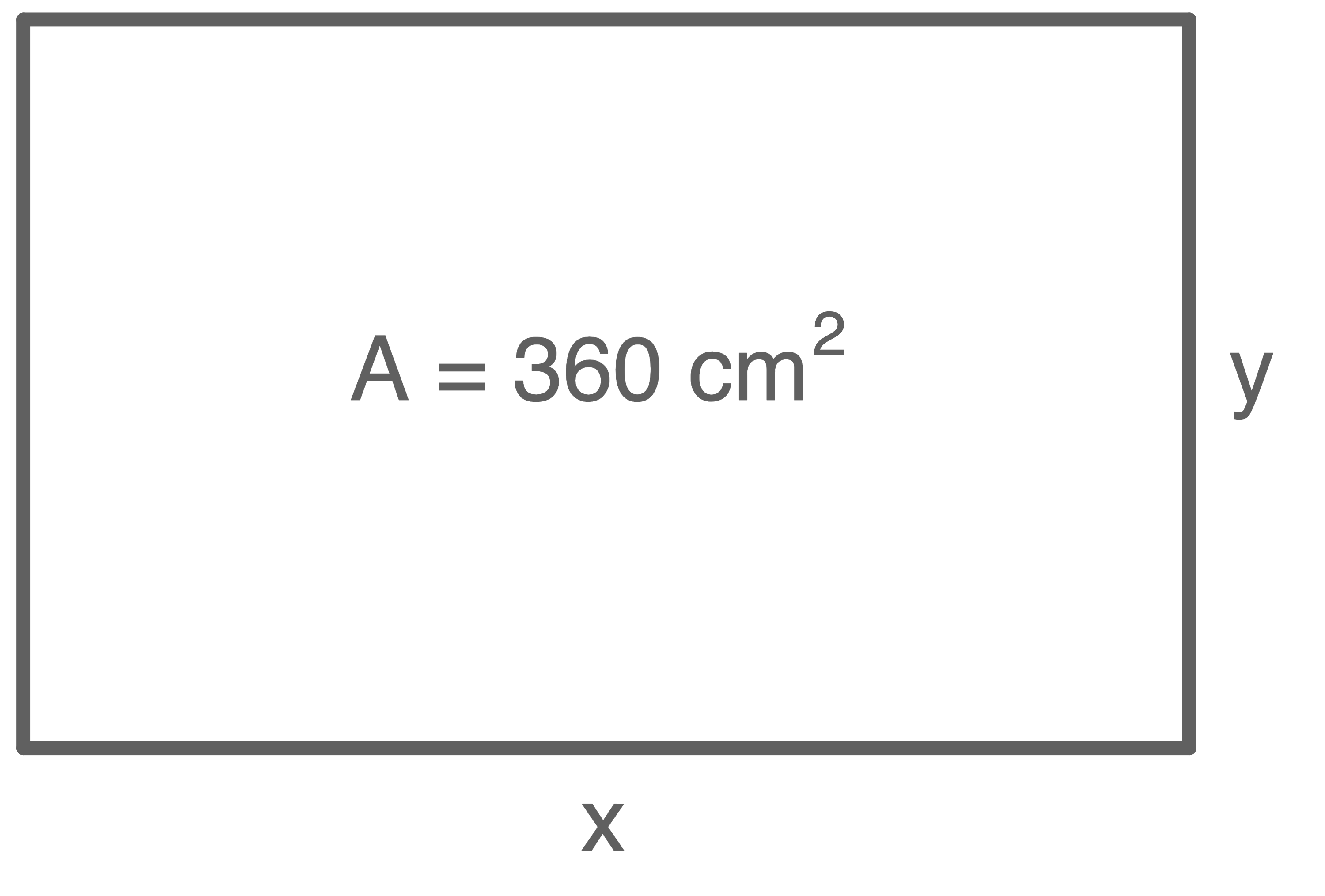

(Skizze nicht maßstabsgetreu)
- Stelle zwei Gleichungen auf.
- Berechne die Länge und Breite des ursprünglichen Rechtecks.
(2 Pkt.)
Wahlaufgabe 3
a)
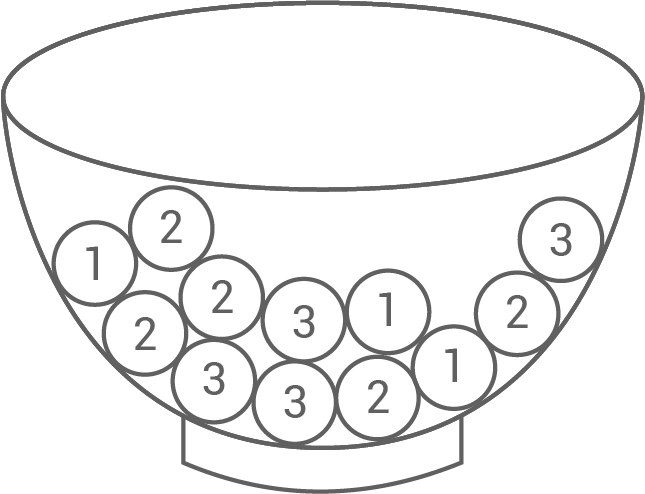
In einem Behälter liegen  Kugeln.
Kugeln.
Sie sind mit oder
oder  oder
oder  beschriftet.
beschriftet.
Es werden zwei Kugeln ohne Zurücklegen gezogen.
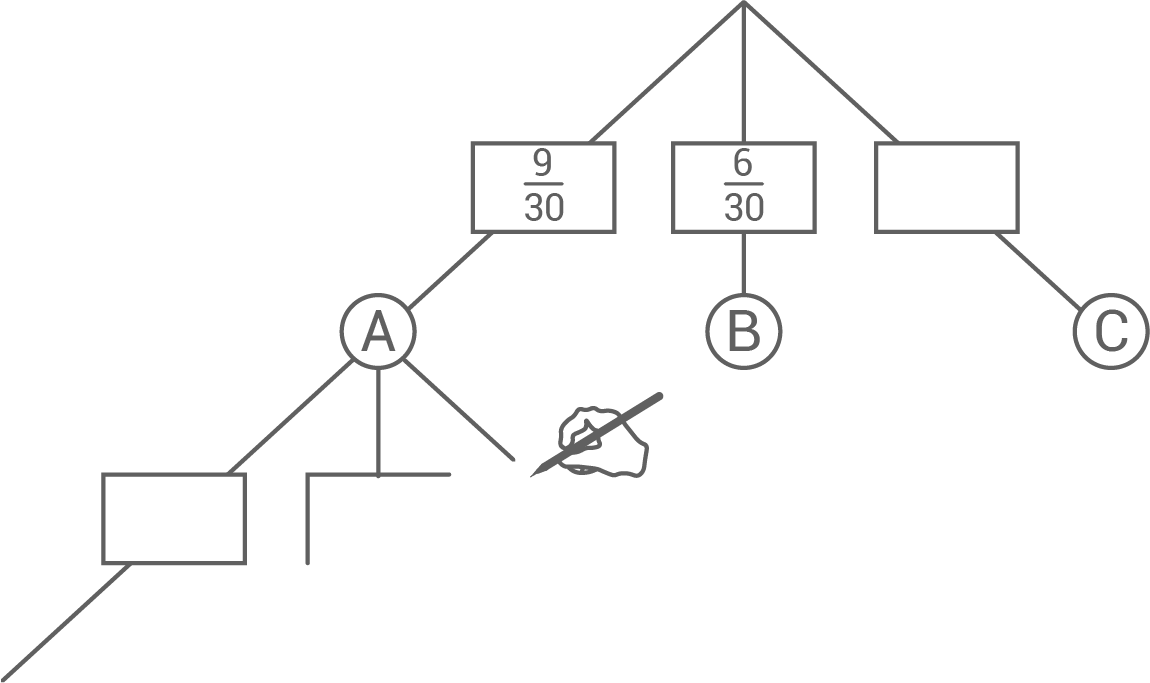
Sie sind mit
Es werden zwei Kugeln ohne Zurücklegen gezogen.

Abbildung 1
- Übertrage und vervollständige das Baumdiagramm (Abbildung 1).

Abbildung 2
- Wie groß ist die Wahrscheinlichkeit, dass die erste gezogene Zahl größer als die zweite gezogene Zahl ist?
(2 Pkt.)
b)
Ein gebrauchtes Auto kostet  Im ersten Jahr beträgt der Wertverlust
Im ersten Jahr beträgt der Wertverlust  ab dem zweiten Jahr durchschnittlich
ab dem zweiten Jahr durchschnittlich 
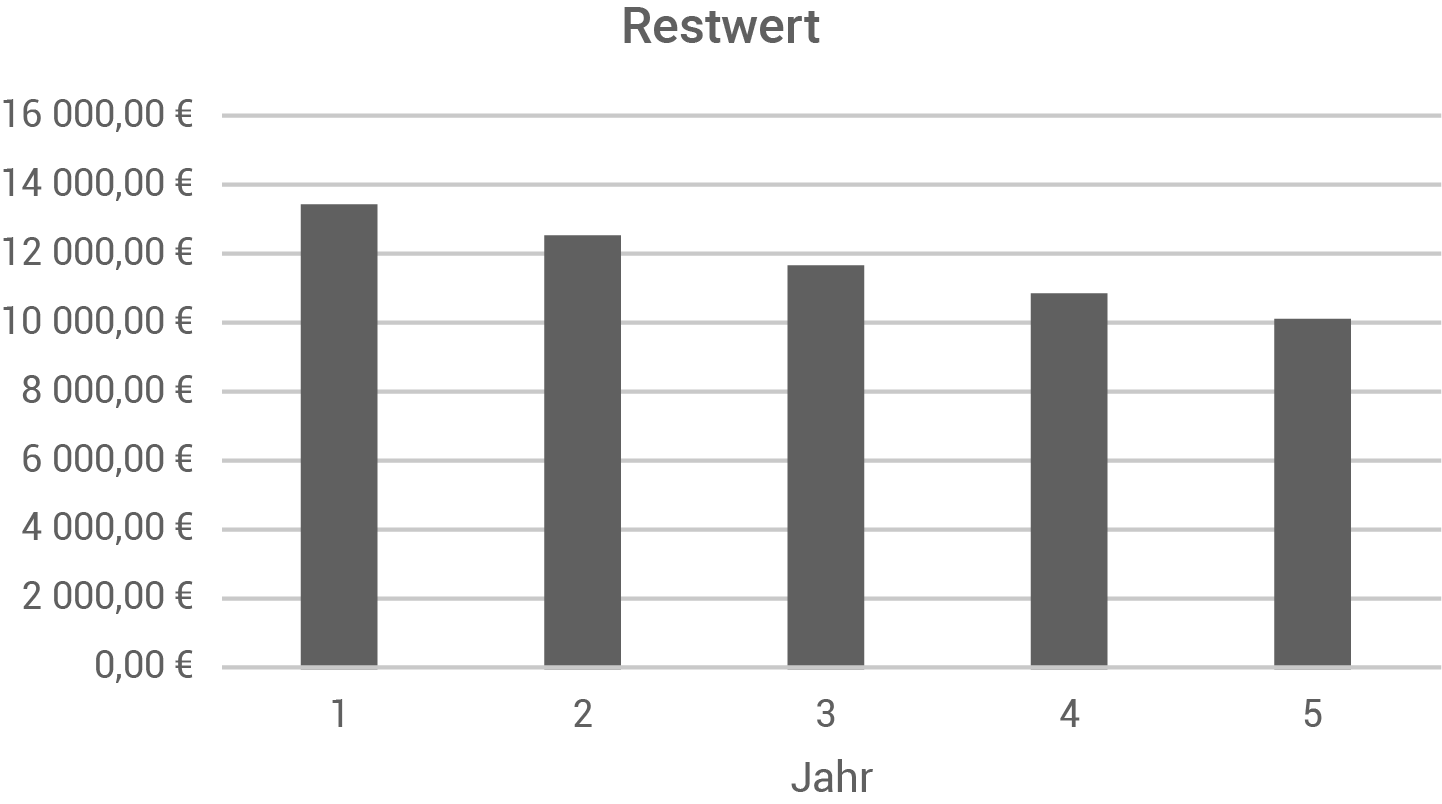
- Bestimme die Restwerte jeweils zum Jahresende der ersten fünf Jahre nach dem Kauf.
- Erstelle für diese Restwerte ein aussagekräftiges Diagramm.
(2 Pkt.)
c)
Von einem Dreieck  kennt man die Höhe
kennt man die Höhe 
 und
und 
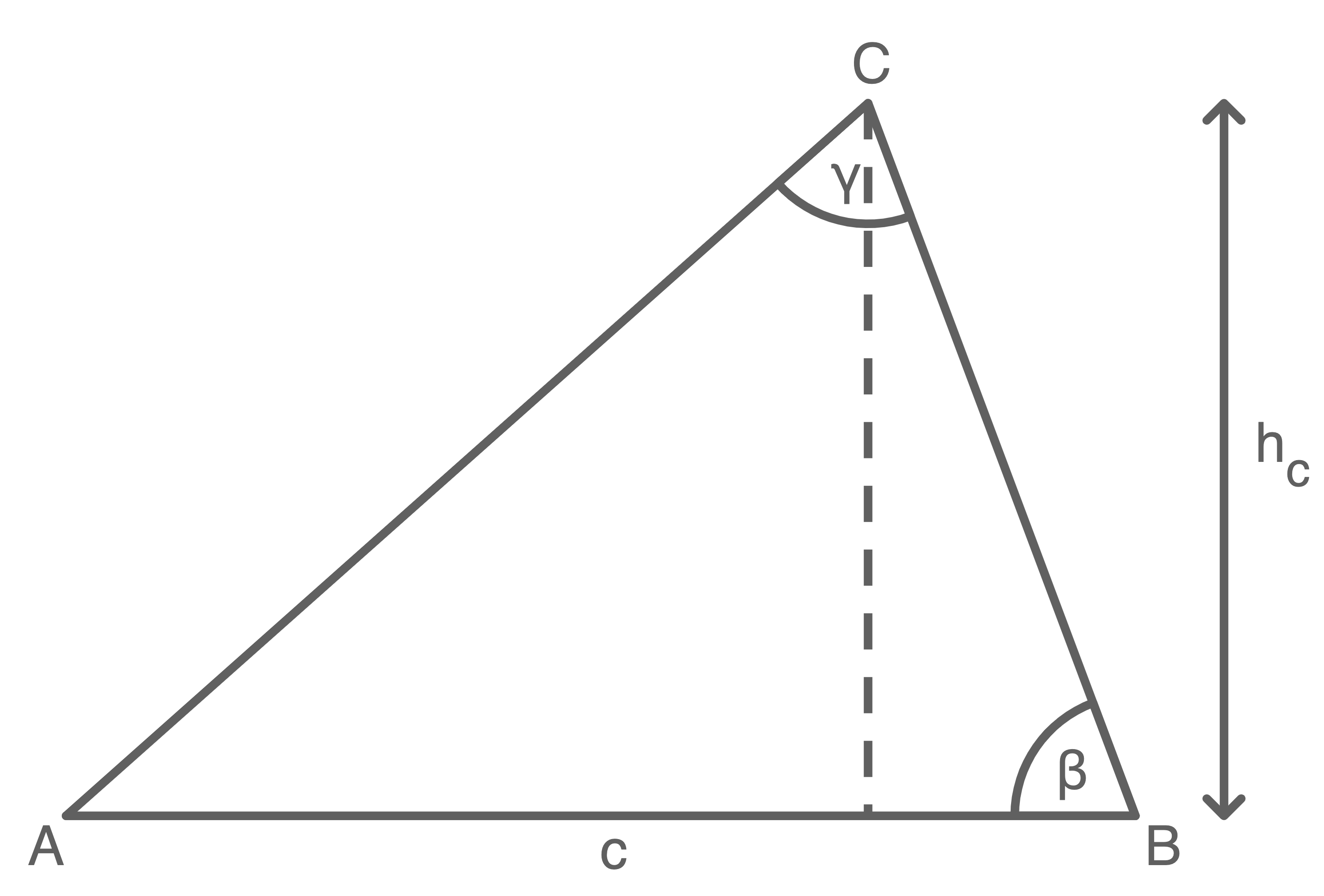
 dieses Dreiecks über die Seite
dieses Dreiecks über die Seite  hinaus auf das Doppelte verlängert, erhält man den Punkt
hinaus auf das Doppelte verlängert, erhält man den Punkt 

(Skizze nicht maßstabsgetreu)
- Berechne die Fläche des Dreiecks.
- Berechne den Umfang des neuen Dreiecks
Wahlaufgabe 4
a)
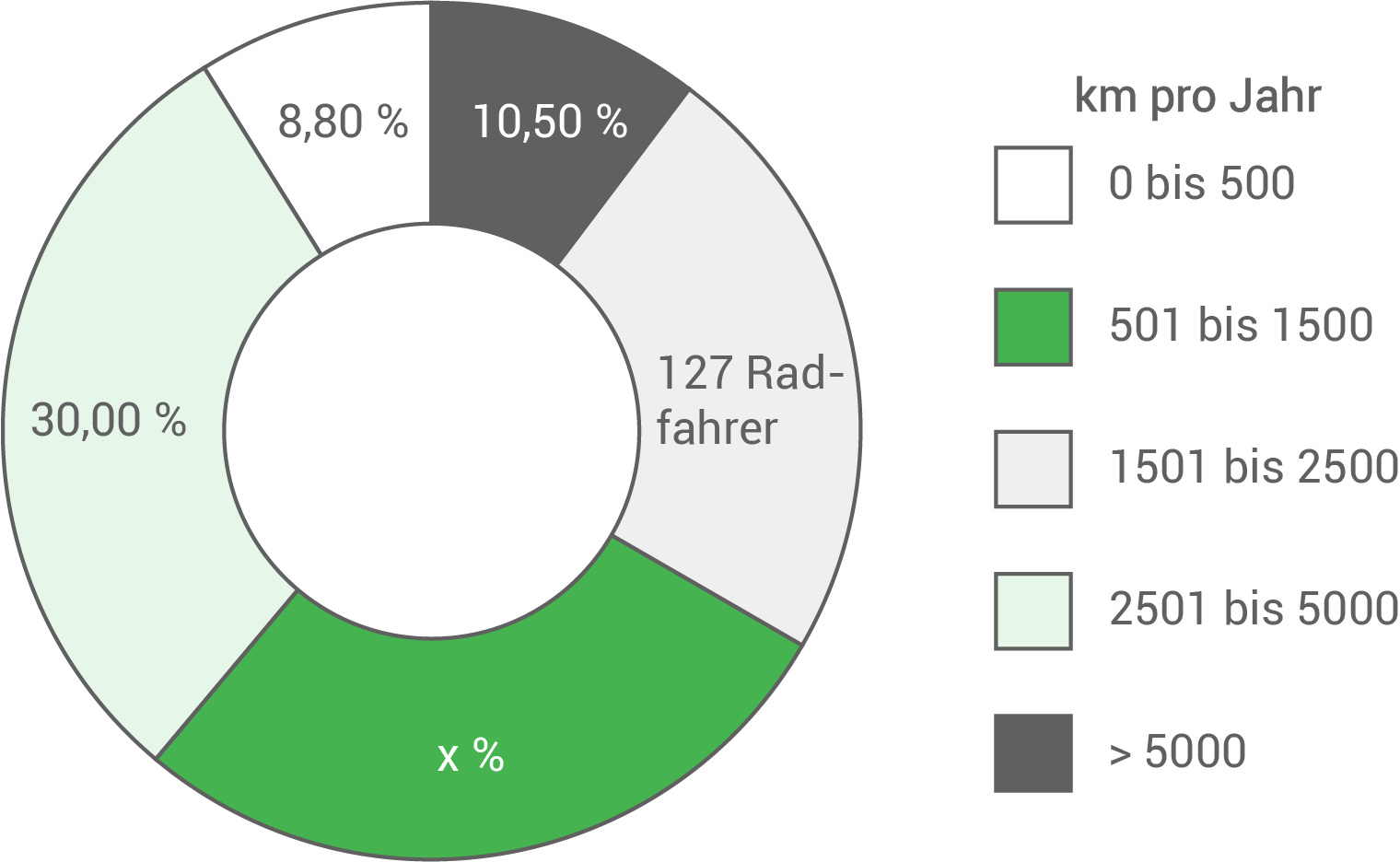
- Berechne die fehlenden Prozentwerte.
- Zwei Aussagen lassen sich eindeutig belegen.
Nenne und begründe diese Aussagen.:
Mehr als die Hälfte der Befragten fährt bis zuKilometer pro Jahr.
:
Jährlich fahren genauRadfahrer mehr als
Kilometer.
MindestensRadfahrer fahren weniger als
Kilometer pro Jahr.
:
Genau einer vonBefragten fährt über
Kilometer pro Jahr.
:
Junge Menschen fahren mehr Fahrrad als ältere Menschen.
(2 Pkt.)
b)
Elvira gewinnt einen Hubschrauberflug zu den bayrischen Königsschlössern Herrenchiemsee, Neuschwanstein und Linderhof.
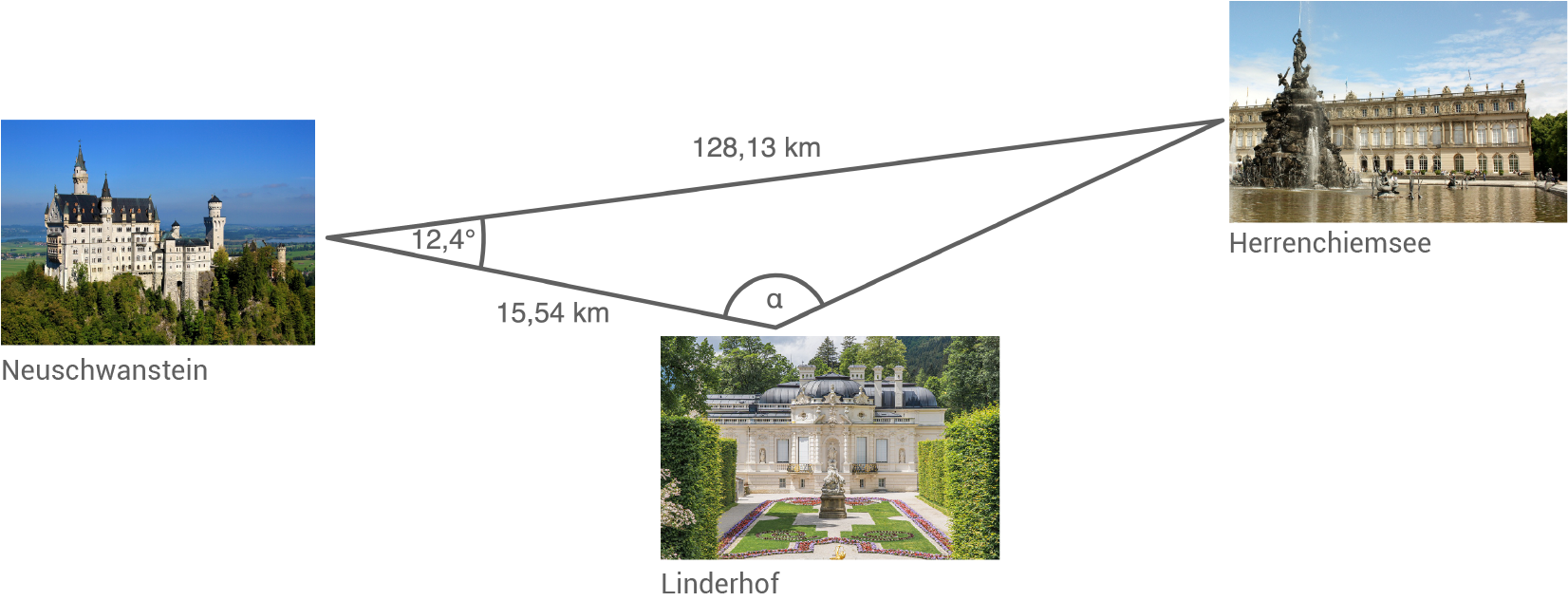

(Skizze nicht maßstabsgetreu)
- Berechne die gesamte Flugstrecke.
- Überprüfe die Behauptung: Der Winkel bei Schloss Linderhof ist ungefähr doppelt so groß wie die beiden anderen Winkel zusammen!
(2 Pkt.)
c)
Am Rande unseres Sonnensystems wird ein neuer Planet vermutet. Seine Masse kann man bereits mit  angeben.
angeben.

Der Erdradius misst  Die mittlere Dichte der Erde beträgt
Die mittlere Dichte der Erde beträgt 
- Vergleiche die Masse des neuen Planeten mit der Masse der Erde.
- Bestimme den Radius des neuen Planeten anhand des Schaubilds.
Masse = Volumen  Dichte
Die Maßzahlen sind gerundet.
Dichte
Die Maßzahlen sind gerundet.
Betrachte beide Planeten als Kugeln.
Vergleich der Oberflächen der Planeten
Betrachte beide Planeten als Kugeln.

(2 Pkt.)
Lösung 1
a)
Die Bodenfläche berechnen
Der Maßstab bedeutet:  in der Abbildung entspricht
in der Abbildung entspricht  in der Wirklichkeit.
Durch Abmessen im Bild ergibt sich für den Durchmesser:
in der Wirklichkeit.
Durch Abmessen im Bild ergibt sich für den Durchmesser:  Hinweis: Je nach Bildschirmgröße kann die Messung variieren. Die Vorgehensweise bleibt jedoch die gleiche.
Somit gilt für den Durchmesser in der Wirklichkeit:
Hinweis: Je nach Bildschirmgröße kann die Messung variieren. Die Vorgehensweise bleibt jedoch die gleiche.
Somit gilt für den Durchmesser in der Wirklichkeit:


![\(\begin{array}{rcl}
1\,\text{cm} & \mathrel{\widehat{=}}& 0,80\,\text{m}\\[5pt]
9\,\text{cm} & \mathrel{\widehat{=}}& 7,20\,\text{m}\\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/bf04324b746498a8f457274ea638e67698c47121ef55efbfd5d021716d5b8d07_light.svg)

 Daraus folgt für den Radius:
Daraus folgt für den Radius:  Damit lässt sich die Bodenfläche berechnen:
Damit lässt sich die Bodenfläche berechnen:
![\(\begin{array}[t]{rll}
A_{\text{Kreis}}&=&\pi\cdot r^2 \\[5pt]
A_{\text{Kreis}}&=&\pi\cdot (3,60\,\text{m})^2 \\[5pt]
A_{\text{Kreis}}&\approx& \boldsymbol{40,7\,\text{m}^2} \\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/2d422607b4ad03e165602841a4dc3b7bde0d4f9beef39cbec149110b4afa1d48_light.svg) Wie viele Quadratmeter hat die vollständig geschlossene Hülle?
Wie viele Quadratmeter hat die vollständig geschlossene Hülle?
![\(\begin{array}[t]{rll}
O&=&\dfrac{1}{2}\cdot 4\cdot \pi\cdot r^2 \\[5pt]
O&=&\dfrac{1}{2}\cdot 4\cdot \pi\cdot (3,6\,\text{m})^2 \\[5pt]
O&\approx&\boldsymbol{81,4\,\text{m}^2} \\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/b8470a6798628a3060f34a35537274c49ff3a13c16b1c0ec16ddd8bb1bbf1bf0_light.svg)
b)
Wie hoch ist Lauras Restschuld nach fünf Monaten?
Kredithöhe:  Monatlicher Zinssatz:
Monatlicher Zinssatz:  Beispiel zur Berechnung der Monatszinsen
Beispiel zur Berechnung der Monatszinsen
 Beispiel zur Berechnung der Summe
Beispiel zur Berechnung der Summe
 Beispiel zur Berechnung der Schulden am Ende
Beispiel zur Berechnung der Schulden am Ende
 Lauras Restschuld nach fünf Monaten beträgt
Lauras Restschuld nach fünf Monaten beträgt  Wie viel Euro Zinsen hat Laura bis zu diesem Zeitpunkt bezahlt?
Wie viel Euro Zinsen hat Laura bis zu diesem Zeitpunkt bezahlt?

 Sie hat bis zu diesem Zeitpunkt
Sie hat bis zu diesem Zeitpunkt  Zinsen bezahlt.
Den Verlauf der Restschuld in einem Diagramm darstellen
Zinsen bezahlt.
Den Verlauf der Restschuld in einem Diagramm darstellen


c)
Zu zwei der Parabeln die dazugehörige Gleichung angeben




 Schnittpunkte berechnen
Die Funktionsgleichung der eingezeichneten Geraden:
Schnittpunkte berechnen
Die Funktionsgleichung der eingezeichneten Geraden:  Damit gilt:
Damit gilt:
![\(\begin{array}[t]{rll}
(x-2)^2+1&=&-x+5 & \\[5pt]
x^2-4x+4+1&=&-x+5 & \\[5pt]
x^2-4x+5&=&-x+5 &\quad \scriptsize \mid\;+x \\[5pt]
x^2-3x+5&=&5 &\quad \scriptsize \mid\;-5 \\[5pt]
x^2-3x&=&0 &\\[5pt]
x\cdot (x-3)&=&0 &
\end{array}\)](https://www.schullv.de/resources/formulas/8f7804884e3a8078a73964e3ad8799f0751c1d7acf61ceea0cb2d8927117ad33_light.svg) Mit dem Satz vom Nullprodukt folgt:
Mit dem Satz vom Nullprodukt folgt:


 -Werte berechnen:
-Werte berechnen:

 Somit gilt für die Schnittpunkte:
Somit gilt für die Schnittpunkte:  und
und 
Lösung 2
a)
Wie viele Möglichkeiten gibt es?
Es gibt 8 Kombinationsmöglichkeiten.
Mit welcher Wahrscheinlichkeit wird genau die Summe 17 gezogen?
Es gilt:

![\(\begin{array}[t]{rll}
&=& P(7;10)+P(10;7)+P(8;9)+P(9;8)\\[5pt]
&=& \dfrac{1}{7}\cdot \dfrac{2}{6}+\dfrac{2}{7}\cdot \dfrac{1}{6}+\dfrac{2}{7}\cdot \dfrac{2}{6}+\dfrac{2}{7}\cdot \dfrac{2}{6}\\[5pt]
&=& \boldsymbol{\dfrac{2}{7}}\\[5pt]
&\approx& 0,286=\boldsymbol{28,6\,\%}\\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/775510ed0e51cf82f3e3598ae60a6a7387be6f86331dc38914bab1a2325158c1_light.svg)
| Karte 1 | Karte 2 |
|---|---|
| 7 | 8 |
| 7 | 9 |
| 7 | 10 |
| 8 | 8 |
| 8 | 9 |
| 8 | 10 |
| 9 | 9 |
| 9 | 10 |
b)
Wie viele Keime enthält ein Liter ungekühlte Milch nach fünf Stunden?
 Nach 5 Stunden enthält ein Liter Milch
Nach 5 Stunden enthält ein Liter Milch  Keime.
Die Wachstumsrate bestimmen
Gegeben:
Keime.
Die Wachstumsrate bestimmen
Gegeben:
![\(\begin{array}[t]{rll}
W_n&=&W_0\cdot q^n & \\[5pt]
W_5&=&W_0\cdot q^5 &\quad \scriptsize \mid\;:W_0 \\[5pt]
\dfrac{W_5}{W_0}&=&q^5 \\[5pt]
q^5&=& \dfrac{W_5}{W_0}&\quad \scriptsize \mid\;\sqrt[5]{\,\,} \\[5pt]
q&=& \sqrt[5]{\dfrac{W_5}{W_0}}& \\[5pt]
q&=& \sqrt[5]{\dfrac{1\,000}{500}}& \\[5pt]
q&\approx&1,149& \\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/4accddd56a5fc677611cc0d15ebc239b6494f18c8d2b9d95a98511eecbfdc706_light.svg)
 Die Wachstumsrate beträgt
Die Wachstumsrate beträgt 
c)
Zwei Gleichungen aufstellen
![\(\begin{array}[t]{rll}
\text{(I)}&x\cdot y&=&360 \\[5pt]
\text{(II)}&2\cdot (x+5)+2\cdot (y+3)&=&92\\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/47c1bca3f98ba68fc14536e24fc75a7b10f13b994570cfdbda4a31f3a3f15e92_light.svg) Länge und Breite des ursprünglichen Rechtecks berechnen
Gleichung
Länge und Breite des ursprünglichen Rechtecks berechnen
Gleichung  nach
nach  auflösen
auflösen
![\(\begin{array}[t]{rll}
\text{(I)}&x\cdot y&=&360 &\quad \scriptsize \mid\;:y \\[5pt]
\text{(I](https://www.schullv.de/resources/formulas/c18d460b296b5d1935a84ec3e7e1c9013e69118ab9a4279af4f51d2f4f625079_light.svg) Gleichung
Gleichung  in Gleichung
in Gleichung  einsetzen
einsetzen
![\(\begin{array}[t]{rll}
2\cdot (x+5)+2\cdot (y+3)&=&92& \\[5pt]
2\cdot \left(\dfrac{360}{y}+5\right)+2\cdot (y+3)&=& 92 \\[5pt]
\dfrac{720}{y}+10+2y+6&=&92\\[5pt]
\dfrac{720}{y}+2y+16&=&92&\quad \scriptsize \mid\;-92 \\[5pt]
\dfrac{720}{y}+2y-76&=&0&\quad \scriptsize \mid\;\cdot y\\[5pt]
720+2y^2-76y&=&0&\quad \scriptsize \mid\;:2\\[5pt]
y^2-38y+360&=&0
\end{array}\)](https://www.schullv.de/resources/formulas/73bce5adce9f1d02e6bbfc750785084669bc692cceb68f8df0c482a301aa601d_light.svg)
![\(\begin{array}[t]{rll}
y_{1/2}&=&-\dfrac{-38}{2}\pm\sqrt{\left(\dfrac{-38}{2}\right)^2-360}&\\[5pt]
y_{1/2}&=&19\pm\sqrt{1}&\\[5pt]
y_{1}&=&19+1=20&\\[5pt]
y_{2}&=&19-1=18&\\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/2e1a7db8a8293034c26660cf295710d78a84a09336f390bb742ac4e8676a3f71_light.svg)
 in Gleichung
in Gleichung  einsetzen
einsetzen

 in Gleichung
in Gleichung  einsetzen
einsetzen
 Die Seitenlängen des ursprünglichen Rechtecks sind
Die Seitenlängen des ursprünglichen Rechtecks sind  und
und 
Lösung 3
a)
Baumdiagramm vervollständigen
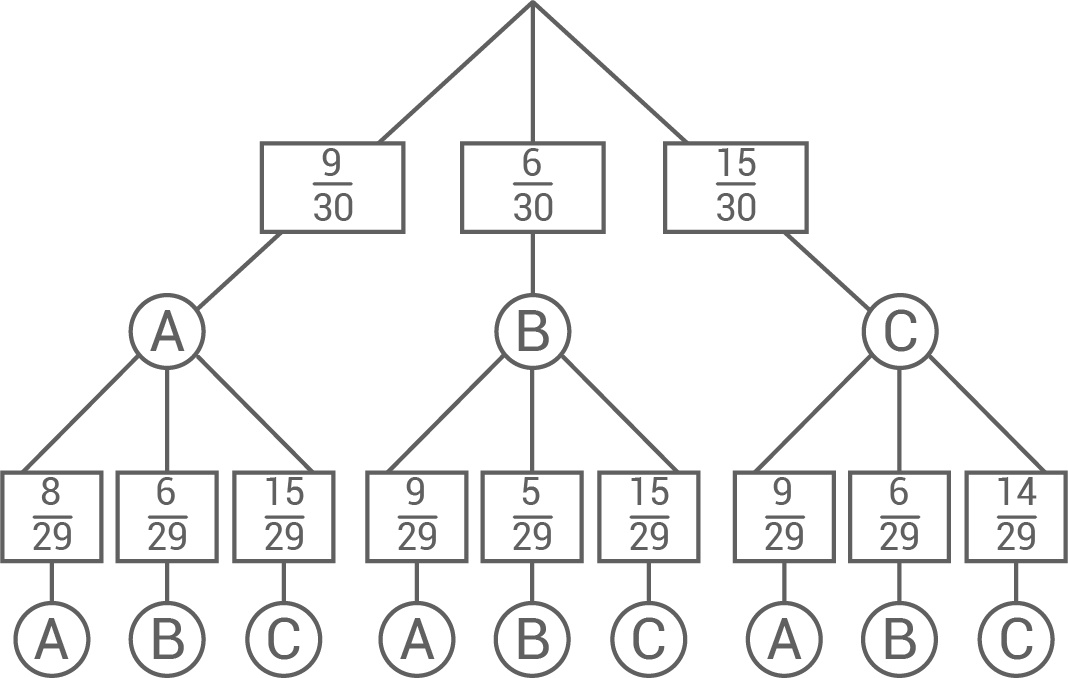 Wie groß ist die Wahrscheinlichkeit, dass die erste gezogene Zahl größer als die zweite gezogene Zahl ist?
Es gilt:
Wie groß ist die Wahrscheinlichkeit, dass die erste gezogene Zahl größer als die zweite gezogene Zahl ist?
Es gilt:

![\(\begin{array}[t]{rll}
&=&P(2;1)+P(3;1)+P(3;2) &\\[5pt]
&=&\dfrac{5}{12}\cdot \dfrac{3}{11}+\dfrac{4}{12}\cdot \dfrac{3}{11}+\dfrac{4}{12}\cdot \dfrac{5}{11} &\\[5pt]
&=&\boldsymbol{\dfrac{47}{132}} &\\[5pt]
&\approx& 0,356=\boldsymbol{35,6\,\%} &\\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/bcc216c4687bf41741ca540364924563201c26262cedbc9c3bae0e04a5ad8144_light.svg)

b)
Restwerte jeweils zum Jahresende der ersten fünf Jahre bestimmen
Beispiel zur Berechnung des Wertverlusts

 Beispiel zur Berechnung des Restwerts
Beispiel zur Berechnung des Restwerts
 Für die Restwerte ein Diagramm erstellen
Für die Restwerte ein Diagramm erstellen

c)
Flächeninhalt des Dreiecks berechnen
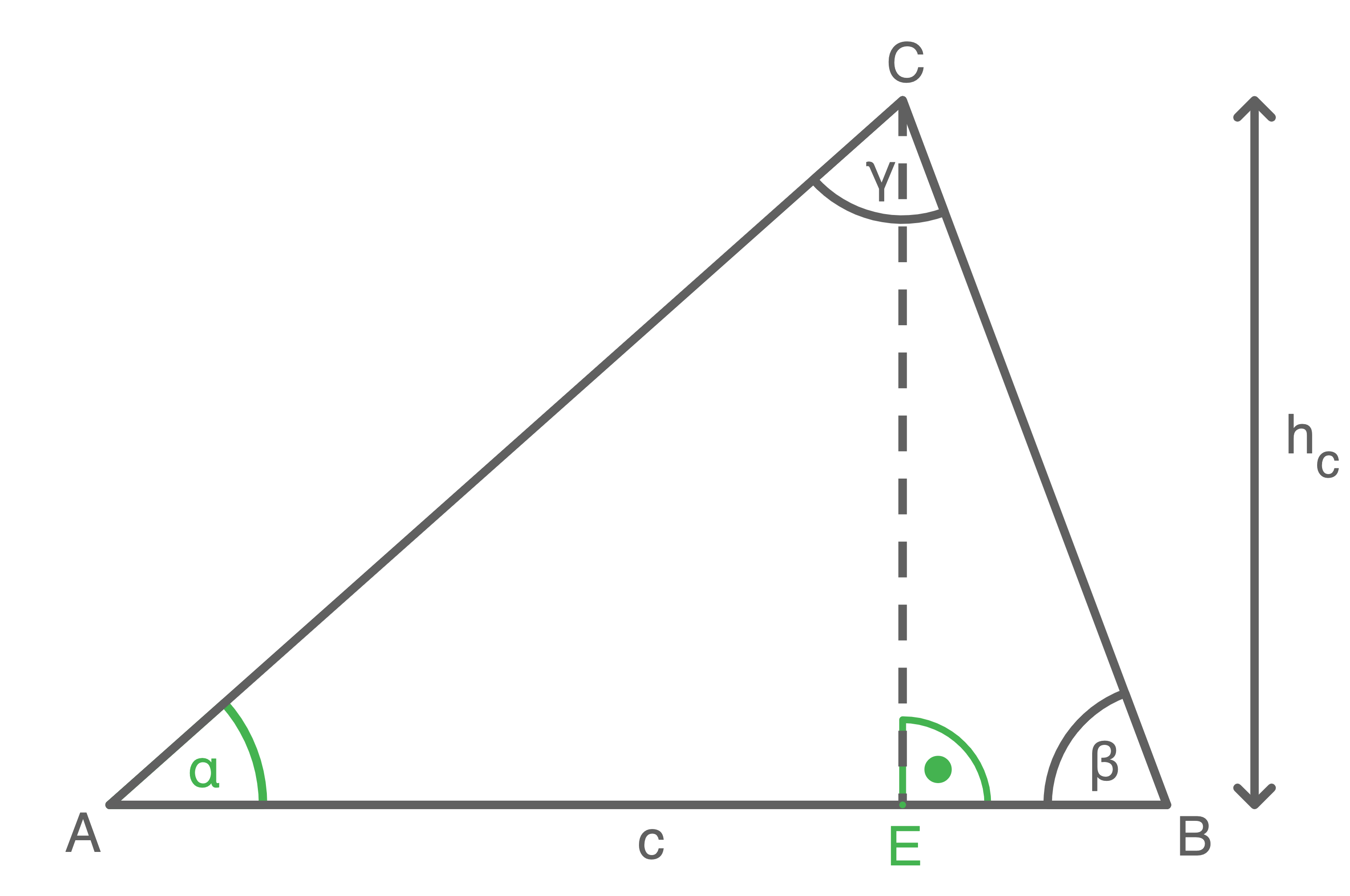 Größe des Winkels
Größe des Winkels  berechnen
berechnen
 Länge von
Länge von  berechnen
berechnen
![\(\begin{array}[t]{rll}
\tan(\alpha)&=& \dfrac{\overline{h_c}}{\overline{AE}}&\quad \scriptsize \mid\;\cdot \overline{AE} \\[5pt]
\tan(\alpha)\cdot \overline{AE}&=& h_c&\quad \scriptsize \mid\;:\tan(\alpha) \\[5pt]
\overline{AE}&=& \dfrac{h_c}{\tan(\alpha)} \\[5pt]
\overline{AE}&=& \dfrac{5,2\,\text{cm}}{\tan(50^{\circ})} \\[5pt]
\overline{AE}&\approx& 4,36\,\text{cm}
\end{array}\)](https://www.schullv.de/resources/formulas/f9842218ae21e0ca4c1105d1051293612b144ea327df95604560d7829f5d400c_light.svg) Länge von
Länge von  berechnen
berechnen
![\(\begin{array}[t]{rll}
\tan(\beta)&=&\dfrac{h_c}{\overline{EB}} &\quad \scriptsize \mid\;\cdot \overline{EB} \\[5pt]
\tan(\beta)\cdot \overline{EB}&=&h_c &\quad \scriptsize \mid\; :\tan(\beta)\\[5pt]
\overline{EB}&=&\dfrac{h_c}{\tan(\beta)} &\\[5pt]
\overline{EB}&=&\dfrac{5,2\,\text{cm}}{\tan(59^{\circ})} &\\[5pt]
\overline{EB}&\approx&3,12\,\text{cm}
\end{array}\)](https://www.schullv.de/resources/formulas/d5f51d3fd18a16e26306eff8cb8b2ac2a539eda7916656a33bc3ebd3d881a55d_light.svg) Länge von c berechnen
Länge von c berechnen
![\(\begin{array}[t]{rll}
c&=& \overline{AE}+\overline{EB}& \\[5pt]
&=& 4,36\,\text{cm}+3,12\,\text{cm}& \\[5pt]
&=& 7,48\,\text{cm}
\end{array}\)](https://www.schullv.de/resources/formulas/d289948eefc8fe7831ee8eb63faab04b1b67735adf22de2a3a777142f723eb34_light.svg) Flächeninhalt berechnen
Flächeninhalt berechnen
![\(\begin{array}[t]{rll}
A&=& \dfrac{c\cdot h_c}{2}\\[5pt]
A&=& \dfrac{7,48\,\text{cm}\cdot 5,2\,\text{cm}}{2}\\[5pt]
A&\approx& \boldsymbol{19,45\,\text{cm}^2}
\end{array}\)](https://www.schullv.de/resources/formulas/d24ade1d4a23677d2d3efef81bf7f5c00d5f9a5284da0873195d65922f5500eb_light.svg) Umfang des neuen Dreiecks berechnen
Umfang des neuen Dreiecks berechnen
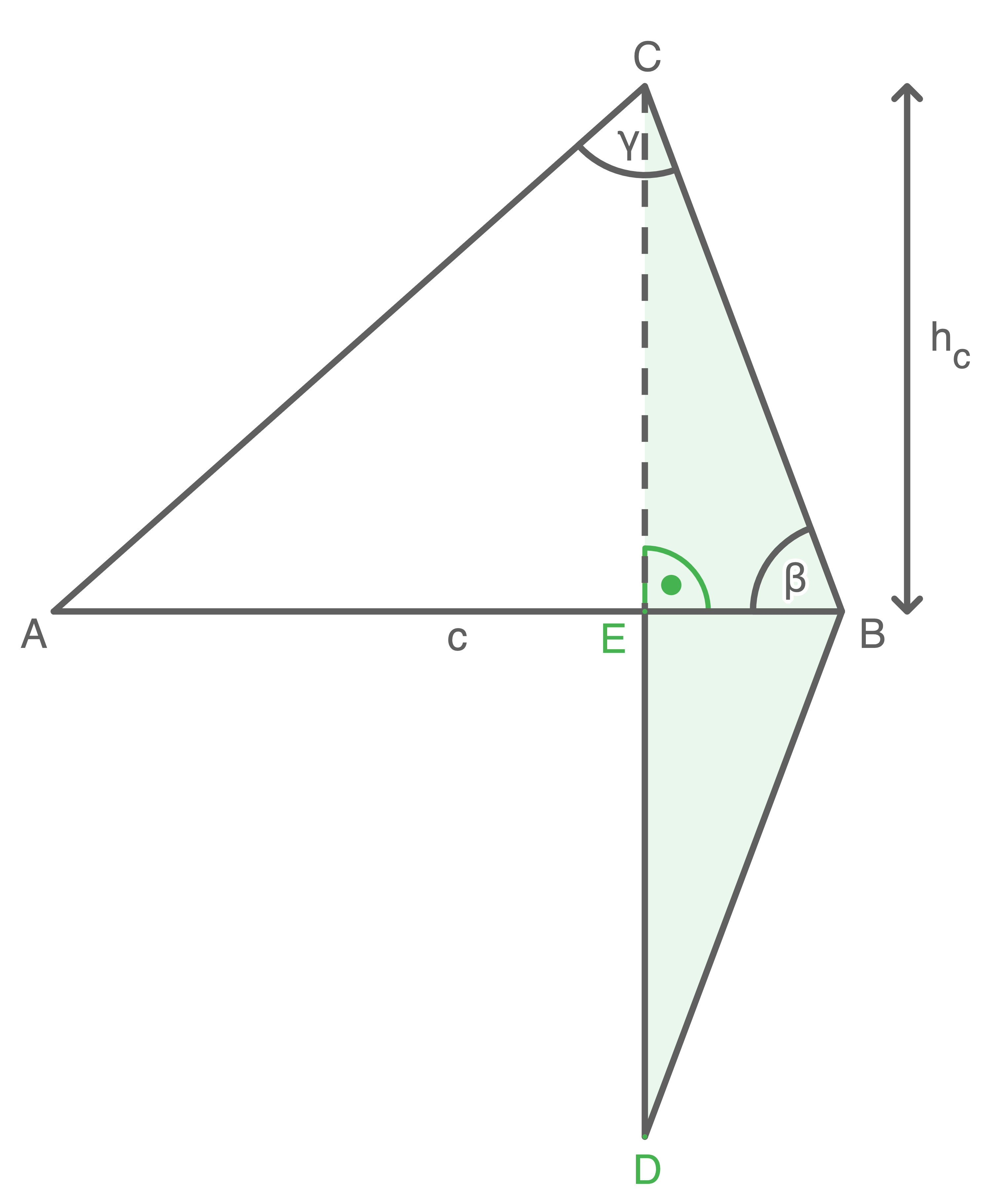 Länge von
Länge von  berechnen
berechnen
![\(\begin{array}[t]{rll}
\overline{BC}^2&=&h_c^{\,\,\,2}+\overline{EB}^2 &\quad \scriptsize \mid\;\sqrt{\,\,} \\[5pt]
\overline{BC}&=&\sqrt{h_c^{\,\,\,2}+\overline{EB}^2} & \\[5pt]
\overline{BC}&=&\sqrt{(5,2\,\text{cm})^{2}+(3,12\,\text{cm})^2} & \\[5pt]
\overline{BC}&\approx&6,1\,\text{cm}
\end{array}\)](https://www.schullv.de/resources/formulas/16db133ce96752b73489a970657390f999b098e55a1c9102f841426fc4ff031a_light.svg) Umfang berechnen
Umfang berechnen
![\(\begin{array}[t]{rll}
u&=&2\cdot h_c+2\cdot\overline{BC} \\[5pt]
u&=&2\cdot 5,2\,\text{cm}+2\cdot6,1\,\text{cm} \\[5pt]
u&=&\boldsymbol{22,6\,\text{cm}}
\end{array}\)](https://www.schullv.de/resources/formulas/42010f0d54b32361fd71b2e234e64148f1c369203712de307d4ed7c211712f0b_light.svg)


Lösung 4
a)
Fehlende Prozentwerte berechnen
Prozentwert für das Segment „1501 bis 2500 km“
 Prozentwert für das Segment „501 bis 1500 km“
Prozentwert für das Segment „501 bis 1500 km“

 Zwei Aussagen nennen, die sich eindeutig belegen lassen
Aussage
Zwei Aussagen nennen, die sich eindeutig belegen lassen
Aussage  lässt sich belegen
Es fahren
lässt sich belegen
Es fahren  der Befragten bis zu
der Befragten bis zu  pro Jahr. Das ist mehr als die Hälfte der Befragten.
Aussage
pro Jahr. Das ist mehr als die Hälfte der Befragten.
Aussage  lässt sich belegen
Es fahren
lässt sich belegen
Es fahren  der Befragten weniger als
der Befragten weniger als  pro Jahr. Das sind
pro Jahr. Das sind  Personen, also mindestens
Personen, also mindestens 
b)
Gesamte Länge der Flugstrecke berechnen
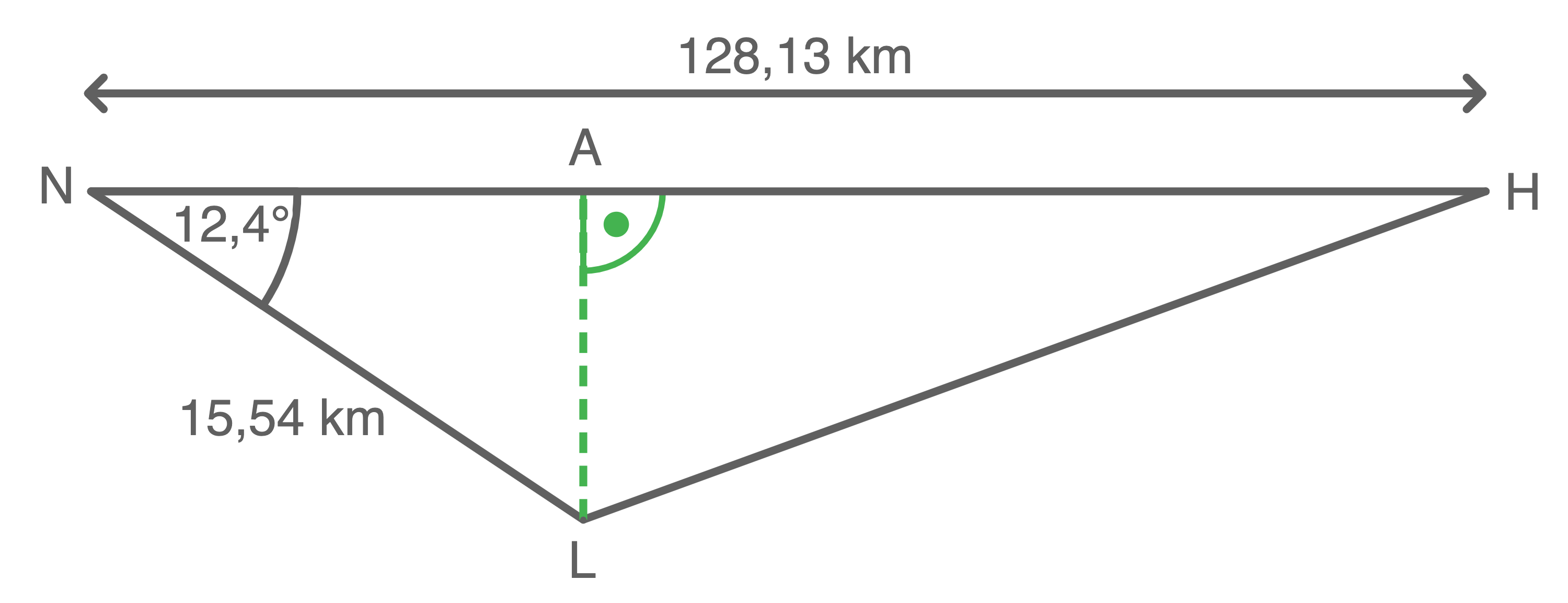 Länge von
Länge von  berechnen
berechnen
![\(\begin{array}[t]{rll}
\cos(12,4^{\circ})&=& \dfrac{\overline{NA}}{15,54\,\text{km}}\quad \scriptsize \mid\;\cdot 15,54\,\text{km} \\[5pt]
\cos(12,4^{\circ})\cdot 15,54\,\text{km} &=& \overline{NA}\\[5pt]
\overline{NA}&=& \cos(12,4^{\circ})\cdot 15,54\,\text{km} \\[5pt]
\overline{NA}&\approx& 15,18\,\text{km} \\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/4a9bc96a7b10db01a7822a6ef8d7174dadce1e7e8a873d63ca00500f846138d9_light.svg) Länge von
Länge von  berechnen
berechnen
![\(\begin{array}[t]{rll}
\overline{AH}&=&\overline{NH}-\overline{NA} \\[5pt]
&=&128,13\,\text{km}-15,18\,\text{km} \\[5pt]
&=&112,95\,\text{km}
\end{array}\)](https://www.schullv.de/resources/formulas/5e65a144e506111a06d196c75e2604c9e452ce9d36e1bda66222d8d89840bf5f_light.svg) Länge von
Länge von  berechnen
berechnen
![\(\begin{array}[t]{rll}
\sin(12,4^{\circ})&=&\dfrac{\overline{AL}}{15,54\,\text{km}} \quad \scriptsize \mid\; \cdot 15,54\,\text{km}\\[5pt]
\sin(12,4^{\circ}) \cdot 15,54\,\text{km}&=&\overline{AL}\\[5pt]
\overline{AL}&=&\sin(12,4^{\circ}) \cdot 15,54\,\text{km}\\[5pt]
\overline{AL}&\approx&3,34\,\text{km}
\end{array}\)](https://www.schullv.de/resources/formulas/3df297619c8e74c46de52af552e5b91455a36690d902eb3fb034491f3a9ed6d1_light.svg) Länge von
Länge von  berechnen
berechnen
![\(\begin{array}[t]{rll}
\overline{LH}^2&=&\overline{AL}^2+\overline{AH}^2 &\quad \scriptsize \mid\; \sqrt{\,\,}\\[5pt]
\overline{LH}&=&\sqrt{\overline{AL}^2+\overline{AH}^2}\\[5pt]
\overline{LH}&=&\sqrt{(3,34\,\text{km})^2+(112,95\,\text{km})^2}\\[5pt]
\overline{LH}&\approx&113\,\text{km}
\end{array}\)](https://www.schullv.de/resources/formulas/7223e81c9866d01663929e9a3a1e1d64b253ca2481422e45711c80cf90826513_light.svg) Gesamte Länge der Flugstrecke berechnen
Gesamte Länge der Flugstrecke berechnen

![\(\begin{array}[t]{rll}
&=& 15,54\,\text{km}+113\,\text{km}+128,13\,\text{km} \\[5pt]
&=&\boldsymbol{256,67\,\text{km}}
\end{array}\)](https://www.schullv.de/resources/formulas/f3bb73c3d96bebe7df3c4bd5cc5c467829f56bb6e2d067c2a703a8a58efd1f3c_light.svg) Behauptung überprüfen
Größe des Winkels bei Schloss Herrenchiemsee
Behauptung überprüfen
Größe des Winkels bei Schloss Herrenchiemsee
![\(\begin{array}[t]{rll}
\tan(\alpha)&=&\dfrac{\overline{AL}}{\overline{AH}} \\[5pt]
\tan(\alpha)&=&\dfrac{3,34\,\text{km}}{112,95\,\text{km}} &\quad \scriptsize \mid\; \tan^{-1}\\[5pt]
\alpha&=&\dfrac{3,34\,\text{km}}{112,95\,\text{km}} \\[5pt]
\alpha&\approx&\boldsymbol{1,7^{\circ}}
\end{array}\)](https://www.schullv.de/resources/formulas/fc93d70684e7e74b302be8af64fbfe412baef7789b588ab700a5378c19ab89ec_light.svg) Größe des Winkels bei Schloss Linderhof
Größe des Winkels bei Schloss Linderhof
 Die Winkel bei Schloss Herrenchiemsee und Neuschwanstein ergeben zusammen:
Die Winkel bei Schloss Herrenchiemsee und Neuschwanstein ergeben zusammen:  Das Doppelte von
Das Doppelte von  ist
ist  Somit ist die Behauptung falsch.
Somit ist die Behauptung falsch.

c)
Masse des neuen Planeten mit der Masse der Erde vergleichen
Volumen der Erde berechnen
![\(\begin{array}[t]{rll}
V&=&\dfrac{4}{3}\cdot \pi\cdot r^3 &\\[5pt]
V&=&\dfrac{4}{3}\cdot \pi\cdot (6\,370\,\text{km})^3 &\\[5pt]
V&\approx&1,083\cdot 10^{12}\,\text{km}^3 &\\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/59ce6e71b60e7ed6c53e9d8990a89e9e2f79b92f6b9302e1754545eaccb371cc_light.svg) Masse der Erde berechnen
Masse der Erde berechnen
![\(\begin{array}[t]{rll}
m&=&1,083\cdot 10^{12}\,\text{km}^3 \cdot 5,515\cdot 10^{12}\,\frac{\text{kg}}{\text{km}^3} \\[5pt]
m&\approx&0,597\cdot 10^{25}\,\text{kg}
\end{array}\)](https://www.schullv.de/resources/formulas/e9c403d0e335e9618b84ec70033045a21bf172e988e75d1dcbab94e99ddbb3f4_light.svg) Der neue Planet ist ca. 10-mal schwerer als die Erde.
Radius des neuen Planeten bestimmen
Oberflächeninhalt der Erde berechnen
Der neue Planet ist ca. 10-mal schwerer als die Erde.
Radius des neuen Planeten bestimmen
Oberflächeninhalt der Erde berechnen
![\(\begin{array}[t]{rll}
O&=&4\cdot \pi\cdot r^2 \\[5pt]
O&=&4\cdot \pi\cdot (6\,370\,\text{km})^2 \\[5pt]
O&\approx&509\,904\,364\,\text{km}^2 \\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/00064c97f6d2b6212a0b051d43d5440c24f1789c6d059ac337acadbdf3f8215b_light.svg) Oberflächeninhalt des neuen Planeten berechnen
Oberflächeninhalt des neuen Planeten berechnen




![\(\begin{array}{rcl}
7,3\,\% & \mathrel{\widehat{=}}& 509\,904\,364\,\text{km}^2\\[5pt]
1\,\% & \mathrel{\widehat{=}}& 69\,849\,912,88\,\text{km}^2\\[5pt]
100\,\% & \mathrel{\widehat{=}}& 6\,984\,991\,288\,\text{km}^2
\end{array}\)](https://www.schullv.de/resources/formulas/f2ddc8e6c3d28898be69532660ce0f487f4f4ff160e66019741052a5c90be6e7_light.svg)



 Radius des neuen Planeten berechnen
Radius des neuen Planeten berechnen
![\(\begin{array}[t]{rll}
O&=&4\cdot \pi\cdot r^2 &\quad \scriptsize \mid\; :4\\[5pt]
\dfrac{O}{4}&=& \pi\cdot r^2 &\quad \scriptsize \mid\; :\pi\\[5pt]
\dfrac{O}{4\cdot \pi}&=& r^2 \\[5pt]
r^2&=& \dfrac{O}{4\cdot \pi} &\quad \scriptsize \mid\; \sqrt{\,\,}\\[5pt]
r&=& \sqrt{\dfrac{6\,984\,991\,288\,\text{km}^2}{4\cdot \pi}} \\[5pt]
r&\approx& \boldsymbol{23\,576\,\text{km}^2}
\end{array}\)](https://www.schullv.de/resources/formulas/366e474923297d2c970aefbe119cdbadf8f23558cb0d61de33b8de60ce848061_light.svg)