Wahlaufgaben
Wahlaufgabe 1
a)
In einer Kiste befinden sich sechs blaue, vier grüne und eine schwarze Kugel. Es wird zweimal ohne Hinschauen und ohne Zurücklegen gezogen.
- Erstelle dazu ein Baumdiagramm
- Wie groß ist die Wahrscheinlichkeit, zuerst eine schwarze und dann eine grüne Kugel zu ziehen?
- Wie groß ist die Wahrscheinlichkeit, zwei gleichfarbige Kuglen zu ziehen?
(2 Pkt.)
b)
Die Zahl der Nutzer stieg anschließend um
*Messenger-Dienste: z.B. WhatsApp, Skype, Facebook Messenger, Snapchat,...
- Wie viele Menschen nutzten nach
Monaten den Messenger-Dienst?
- Nach wie vielen Monaten hatte der Messenger-Dienst bei gleichem Wachstum erstmals mehr als
Millionen Nutzer?
- Berechne die jeweilige monatliche Zunahme der Nutzer für die Monate Mai bis Oktober 2013 und stelle diese in einem aussagekräftigen Diagramm dar.
(2 Pkt.)
c)
Ein Metalllwürfel wird in ein mit Wasser gefülltes zylinderförmiges Gefäß gegeben.
Der Wasserspiegel steigt dadurch um an.
an.
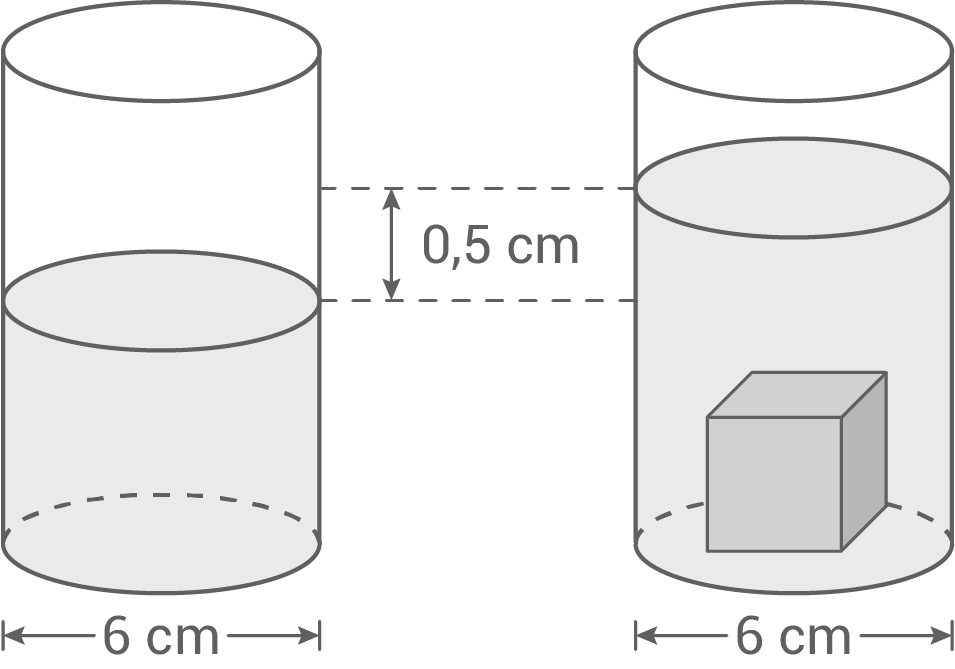
 ist doppelt so lang wie die eines Würfels
ist doppelt so lang wie die eines Würfels 
Der Wasserspiegel steigt dadurch um

(Skizze nicht maßstabsgetreu)
Volumen der verdrängten Flüssigkeit
=
Volumen des Würfels
=
Volumen des Würfels
- Berechne die Kantenlänge des Metallwürfels.
- Vergleiche das Volumen der beiden Würfel prozentual.
(2 Pkt.)
Wahlaufgabe 2
a)
Die abgebildete Person ist etwa  groß.
groß.



- Ermittle das Volumen und die Oberfläche (ohne die kreisförmige Grundfläche) der Halbkugel.
- Bestimme den Flächeninhalt des größtmöglichen regelmäßigen Fünfecks, das in den Kreis passt.
(2 Pkt.)
b)
Ein Gebrauchtwagen kostet 
Von seinen Eltern bekommt Julian für die Anzahlung. Den Rest finanziert er über einen Ratenkredit.
für die Anzahlung. Den Rest finanziert er über einen Ratenkredit.
Von seinen Eltern bekommt Julian
- Anzahlung:
- Monatliche Rate:
- Zins:
p.a.
- Ergänze die Tabelle für die ersten sechs Monate der Kreditlaufzeit.
Monat Kredit in €
MonatsanfangRate in € Zins in € Tilgung in € Kredit in €
Monatsende
- Welcher Betrag des Kredits ist nach 6 Monaten getilgt?
(2 Pkt.)
c)
Der Bogen der abgebildeten Talbrücke kann durch die Funktionsgleichung  beschrieben werden.
beschrieben werden.

(Skizze nicht maßstabsgetreu)
- Berechne den Abstand zwischen Punkt
und Punkt
- Berechne die Strecke
auf der
-Achse.
(2 Pkt.)
Wahlaufgabe 3
a)
Im Dachbereich eines Hauses ist ein Zimmer eingebaut.
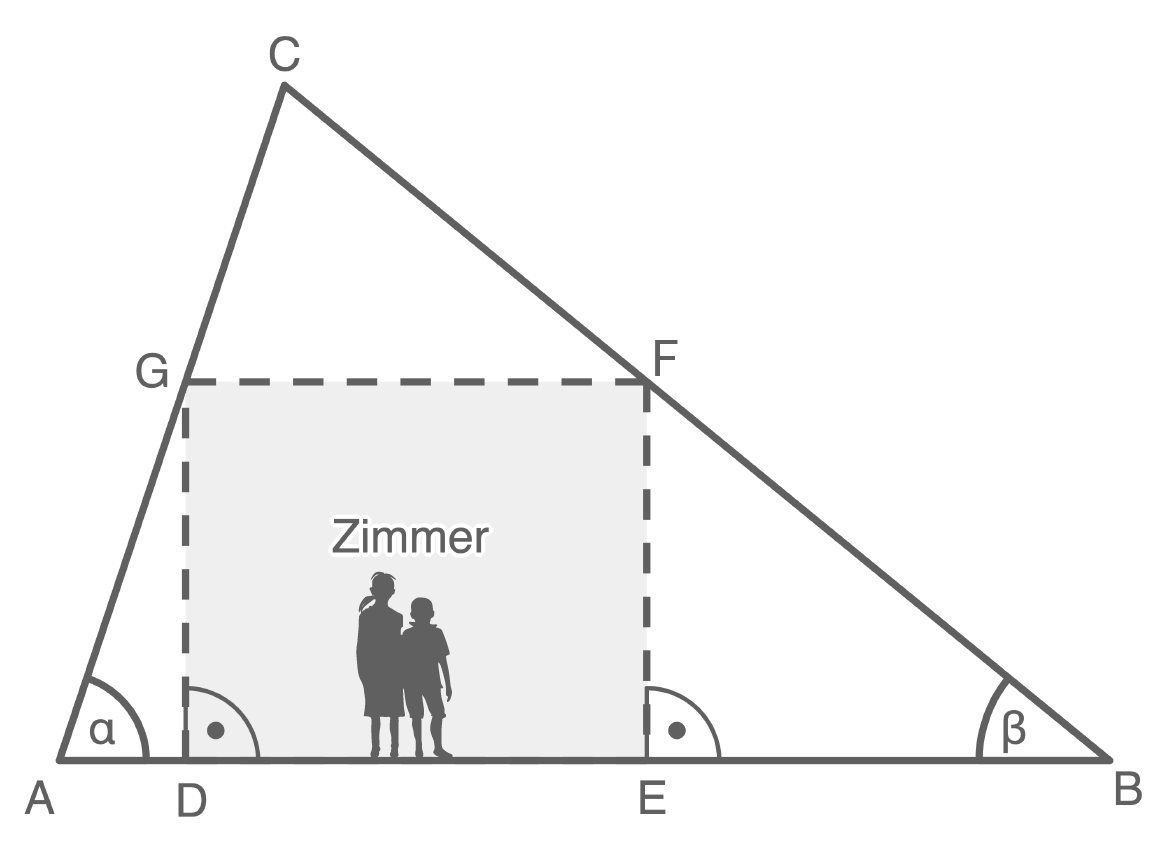
 genau
genau  betragen.
betragen.

(Skizze nicht maßstabsgetreu)
- Berechne
- Berechne nun die maximale Länge der Strecke
.
(2 Pkt.)
b)
Im Jahr 2010 wurden für Kaffeemaschinen  Kaffee in Kapseln verkauft.
Kaffee in Kapseln verkauft.
2015 waren es Kaffee.
Kaffee.
 gerechnet.
gerechnet.
2015 waren es
- Berechne das durchschnittliche jährliche Wachstum für die Zeit von 2010 bis 2015 in Prozent.
- Wie viele Kapseln werden im Jahr 2018 verkauft, wenn jede Kaffeekapsel
Kaffee enthält?
(2 Pkt.)
c)
Die abgebildete Parabel  wird zuerst an der
wird zuerst an der  -Achse, dann an der
-Achse, dann an der  -Achse gespiegelt.
-Achse gespiegelt.
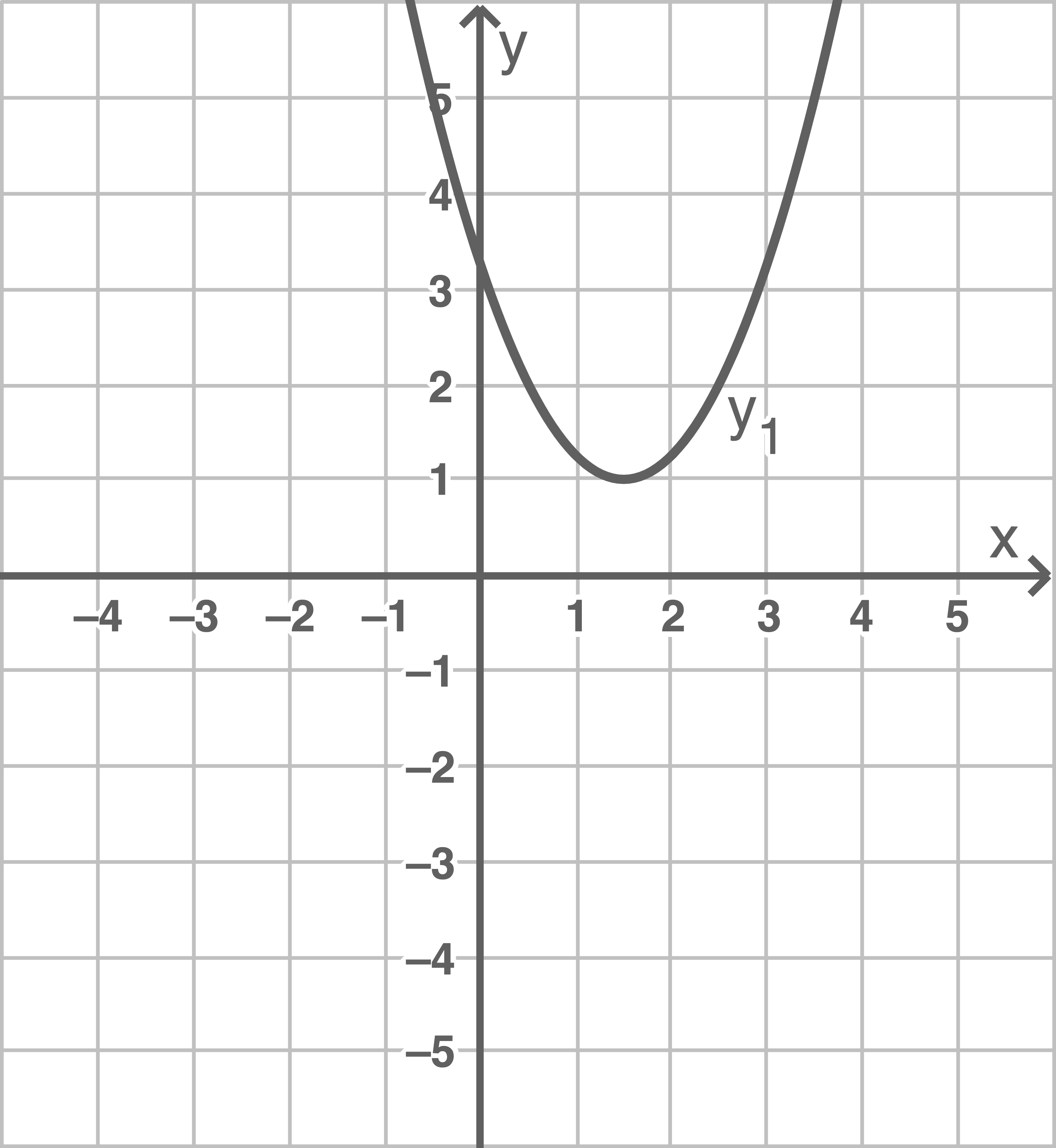

(Skizze nicht maßstabsgetreu)
- Gib die neue Funktionsgleichung an.
- Überprüfe rechnerisch, ob die Gerade mit der Funktionsgleichung
die abgebildete Parabel
schneidet, und bestimme gegebenenfalls den Schnittpunkt.
(2 Pkt.)
Wahlaufgabe 4
a)
Im 17. Jahrhundert besiedelten Holländer das Gebiet des heutigen New Yorks.
1626 kauften sie die Insel Manhattan von den Ureinwohnern Nordamerikas. Sie bezahlten mit Waren im Wert von Dollar.
Dollar.
(Quelle: NYC Government)
1626 kauften sie die Insel Manhattan von den Ureinwohnern Nordamerikas. Sie bezahlten mit Waren im Wert von
- Bestimme den Wert der Insel im Jahr 2018 bei einer angenommenen jährlichen Wertsteigerung von
.
| Jahr | Einwohner |
|---|---|
| 1800 | |
| 1850 | |
| 1900 | |
| 1950 | |
| 2000 |
- In welchem Zeitabschnitt war die prozentuale Zunahme der Bevölkerung am größten?
Berechne den entsprechenden Prozentsatz.
(2 Pkt.)
b)
Patrick kauft sich einen Spielzeugsafe. Dieser hat 3 Tasten, die mit  ,
,  und
und  beschriftet sind (siehe Abbildung).
beschriftet sind (siehe Abbildung).
 Es können damit 3-stellige Kombinationen gebildet werden.
Es können damit 3-stellige Kombinationen gebildet werden.
Der „Innenraum“ des Safes hat ein Volumen von 
- Wie viele unterschiedliche Kombinationen gibt es, bei denen eine Zahl genau zweimal vorkommt? Die Zahlenfolge muss beachtet werden.
Eine quatratische Pyramide hat das gleiche Volumen.
Bei dieser Pyramide ist die Seitenlänge
- Berechne die Höhe
der quadratischen Pyramide.
(2 Pkt.)
c)
Eine Bergbahn fährt von der Talstation über die Mittelstation zur Bergstation.
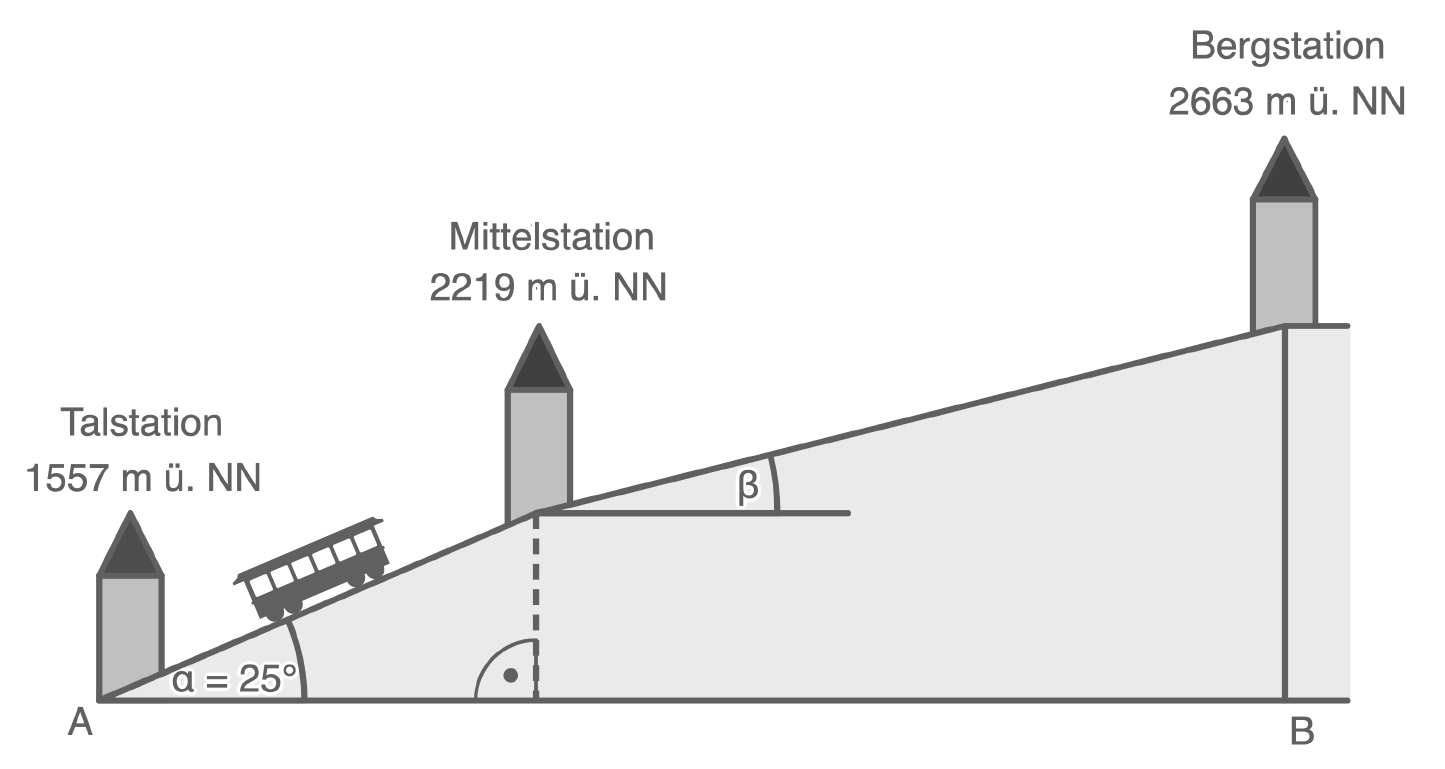


(Skizze nicht maßstabsgetreu)
- Berechne die Streckenlänge zwischen der Tal- und der Mittelstation.
- Berechne den Winkel
- Berechne den Abstand
(2 Pkt.)
Lösung 1
a)
Baumdiagramm erstellen
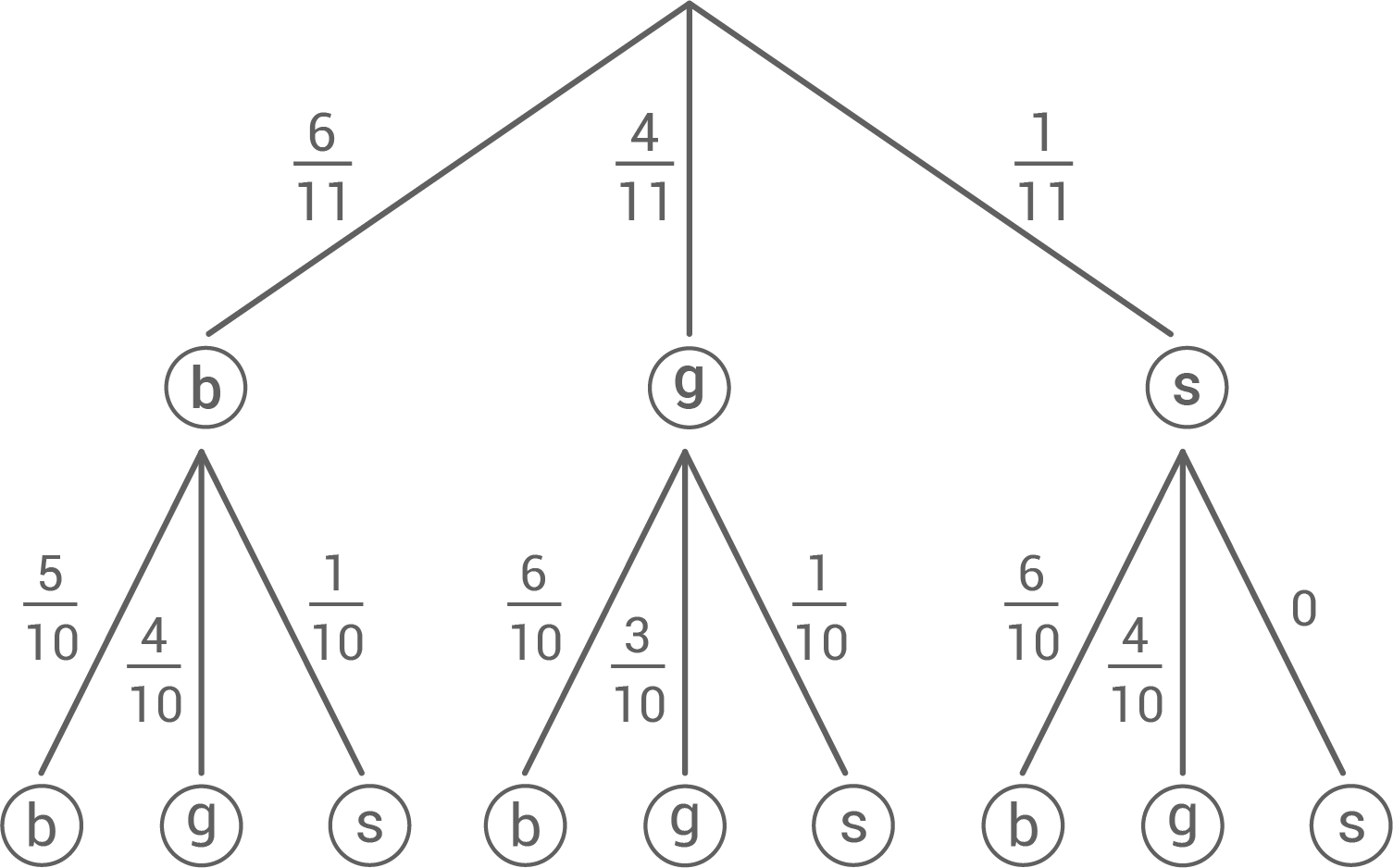 Wie groß ist die Wahrscheinlichkeit, zuerst eine schwarze und dann eine grüne Kugel zu ziehen?
Wie groß ist die Wahrscheinlichkeit, zuerst eine schwarze und dann eine grüne Kugel zu ziehen?
![\(\begin{array}[t]{rll}
P(\text{s; g})&=&\dfrac{1}{11}\cdot \dfrac{4}{10} \\[5pt]
&=&\boldsymbol{\dfrac{2}{55}} \\[5pt]
&\approx&0,036=\boldsymbol{3,6\,\%}
\end{array}\)](https://www.schullv.de/resources/formulas/102afd5fb4f66039a1a86cd5728dbdcf62944cbf543a4905a33cfd6b2ee5282d_light.svg) Wie groß ist die Wahrscheinlichkeit, zwei gleichfarbige Kuglen zu ziehen?
Wie groß ist die Wahrscheinlichkeit, zwei gleichfarbige Kuglen zu ziehen?

![\(\begin{array}[t]{rll}
=&P(\text{b; b})+P(\text{g; g})+P(\text{s; s}) \\[5pt]
=&\dfrac{6}{11}\cdot\dfrac{5}{10} +\dfrac{4}{11}\cdot\dfrac{3}{10}+\dfrac{1}{11}\cdot0 \\[5pt]
=&\boldsymbol{\dfrac{21}{55}}\\[5pt]
\approx&0,382=\boldsymbol{38,2\,\%}
\end{array}\)](https://www.schullv.de/resources/formulas/a21303d65b3e442e2d53d9e26f2484c461889fe135c3e301bd48d923d06197fc_light.svg)

b)
Wie viele Menschen nutzten nach 24 Monaten den Messenger-Dienst?
Gegeben:
![\(\begin{array}[t]{rll}
W_n&=&W_0\cdot \left(1+\dfrac{p}{100}\right)^n \\[5pt]
W_{24}&=&200\,\text{Mio.}\cdot \left(1+\dfrac{6}{100}\right)^{24} \\[5pt]
W_{24}&\approx&\boldsymbol{809,8 \,\text{Mio.}}
\end{array}\)](https://www.schullv.de/resources/formulas/df902ce6de67f0d7cded06b60defb69e118865986bf194da29df312ed4779082_light.svg) Nach 24 Monaten nutzten ca.
Nach 24 Monaten nutzten ca.  Menschen den Messenger-Dienst.
Nach wie vielen Monaten hatte der Messenger-Dienst erstmals mehr als 300 Mio. Nutzer?
Menschen den Messenger-Dienst.
Nach wie vielen Monaten hatte der Messenger-Dienst erstmals mehr als 300 Mio. Nutzer?
![\(\begin{array}{ll}
\text{April}& 200\,\text{Mio.}\\[15pt]
\text{Mai}& 212\,\text{Mio.}\\[15pt]
\text{Juni}& \approx 224,7\,\text{Mio.}\\[15pt]
\text{Juli}& \approx 238,2\,\text{Mio.}\\[15pt]
\text{August}& \approx 252,5\,\text{Mio.}\\[15pt]
\text{September}& \approx 267,7\,\text{Mio.}\\[15pt]
\text{Oktober}& \approx 283,8\,\text{Mio.}\\[15pt]
\text{November}& \approx 300,8\,\text{Mio.}
\end{array}\)](https://www.schullv.de/resources/formulas/5efb1700b3139303d82328494f2706b92c1cd05bba43980864fc0d32115bc14d_light.svg)













 Nach 7 Monaten, also im November 2013, waren es erstmals mehr als 300 Mio. Nutzer.
Die monatliche Zunahme der Nutzer berechnen
Mai
Nach 7 Monaten, also im November 2013, waren es erstmals mehr als 300 Mio. Nutzer.
Die monatliche Zunahme der Nutzer berechnen
Mai
 Juni
Juni
 Juli
Juli
 August
August
 September
September
 Oktober
Oktober
 Ergebnisse in einem Diagramm darstellen
Ergebnisse in einem Diagramm darstellen
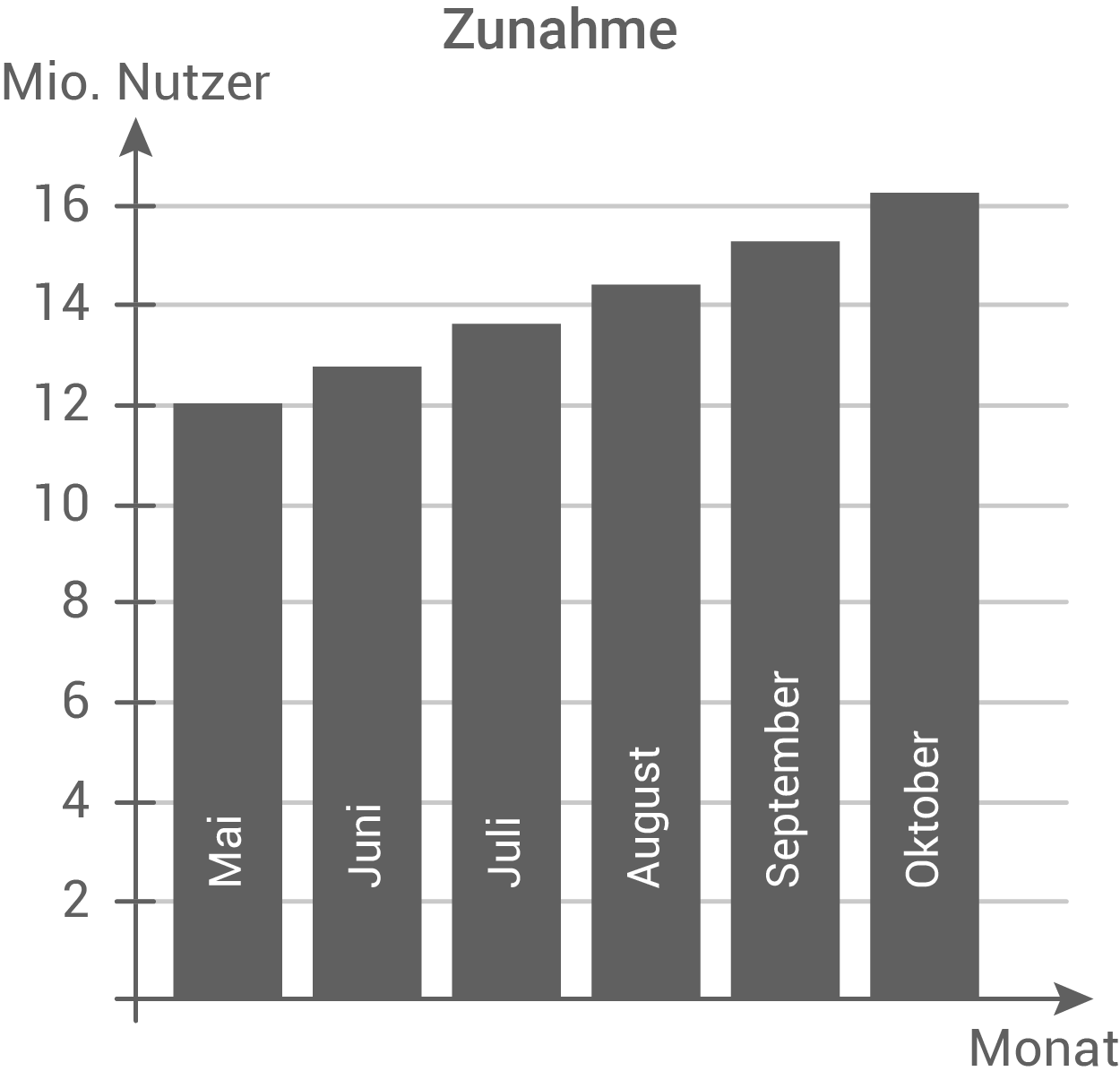
Nutzer
Monate

c)
Kantenlänge des Metallwürfels berechnen
Volumen der verdrängten Flüssigkeit:
![\(\begin{array}[t]{rll}
V&=&\pi\cdot r^2\cdot h \\[5pt]
V&=&\pi\cdot (3\,\text{cm})^2\cdot 0,5\,\text{cm} \\[5pt]
V&\approx&14,137\,\text{cm}^3
\end{array}\)](https://www.schullv.de/resources/formulas/11d082ec89360fa379a4fd377ec7226c7aa0905b2e3d4e9f45e73d28631b8999_light.svg) Da das Volumen der verdrängten Flüssigkeit dem Volumen des Würfels entspricht, kann damit die Kantenlänge berechnet werden:
Da das Volumen der verdrängten Flüssigkeit dem Volumen des Würfels entspricht, kann damit die Kantenlänge berechnet werden:
![\(\begin{array}[t]{rll}
V&=&a^3\\[5pt]
a^3&=&V&\quad \scriptsize \mid\;\sqrt[3]{\,\,} \\[5pt]
a&=&\sqrt[3]{V} \\[5pt]
a&=&\sqrt[3]{14,137\,\text{cm}^3} \\[5pt]
a&\approx&\boldsymbol{2,4\,\text{cm}}
\end{array}\)](https://www.schullv.de/resources/formulas/ce207dab23ad5ac1e396bfa134d3eae53037d02ca57d1d4301f93516309ca068_light.svg) Volumen der beiden Würfel prozentual vergleichen
Volumen von Würfel A:
Volumen der beiden Würfel prozentual vergleichen
Volumen von Würfel A:  Volumen von Würfel B:
Volumen von Würfel B:  Prozentualer Vergleich:
Prozentualer Vergleich:
Das Volumen von Würfel A ist um größer als das Volumen von Würfel B, also um
größer als das Volumen von Würfel B, also um  Alternativer prozentualer Vergleich:
Alternativer prozentualer Vergleich:
Das Volumen von Würfel A ist 8-mal so groß wie das Volumen von Würfel B.
Das Volumen von Würfel A beträgt also des Volumens von Würfel B.
des Volumens von Würfel B.
Das Volumen von Würfel A ist um
Das Volumen von Würfel A ist 8-mal so groß wie das Volumen von Würfel B.
Das Volumen von Würfel A beträgt also
Lösung 2
a)
Volumen der Halbkugel ermitteln
Um den realen Durchmesser der Halbkugel berechnen zu können, werden der Durchmesser und die Größe der Person in der Abbildung abgemessen:




![\(\begin{array}{rcl}
2,1\,\text{cm} & \mathrel{\widehat{=}}& 1,45\,\text{m}\\[5pt]
1\,\text{cm} & \mathrel{\widehat{=}}& \dfrac{1,45}{2,1}\,\text{m}\\[5pt]
5,2\,\text{cm} & \mathrel{\widehat{=}}&\dfrac{1,45}{2,1}\cdot 5,2\,\text{m}\\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/465ebb84955f44c275429072af124e2940b573300faa40a108100527e880bc89_light.svg)




 Damit folgt für den Radius:
Damit folgt für den Radius:  Damit folgt für das Volumen:
Damit folgt für das Volumen:
![\(\begin{array}[t]{rll}
V_H&=&\dfrac{1}{2}\cdot\dfrac{4}{3}\cdot \pi\cdot r^3 \\[5pt]
V_H&=&\dfrac{2}{3}\cdot \pi\cdot (1,8\,\text{m})^3 \\[5pt]
V_H&\approx&\boldsymbol{12,2\,\text{m}^3}
\end{array}\)](https://www.schullv.de/resources/formulas/53f4e7f80d476fdf9aa8ba3d7389d810f13545022dca31920f82b68a1f7cd7fd_light.svg) Oberflächinhalt der Halbkugel ermitteln
Oberflächinhalt der Halbkugel ermitteln
![\(\begin{array}[t]{rll}
O_H&=&\dfrac{1}{2}\cdot 4\cdot \pi\cdot r^2 &\\[5pt]
O_H&=&2\cdot \pi\cdot (1,8\,\text{m})^2 &\\[5pt]
O_H&\approx&\boldsymbol{20,4\,\text{m}^2}
\end{array}\)](https://www.schullv.de/resources/formulas/e6e9476645cbd32c0a0162afddf7a7b5f9df7067cb9b094c5222ce1791a99ec0_light.svg) Flächeninhalt des größtmöglichen regelmäßigen Fünfecks bestimmen
Ein regelmäßiges Fünfeck besteht aus
Flächeninhalt des größtmöglichen regelmäßigen Fünfecks bestimmen
Ein regelmäßiges Fünfeck besteht aus  kongruenten Dreiecken mit dem Mittelpunktswinkel
kongruenten Dreiecken mit dem Mittelpunktswinkel  und den Schenkeln
und den Schenkeln 
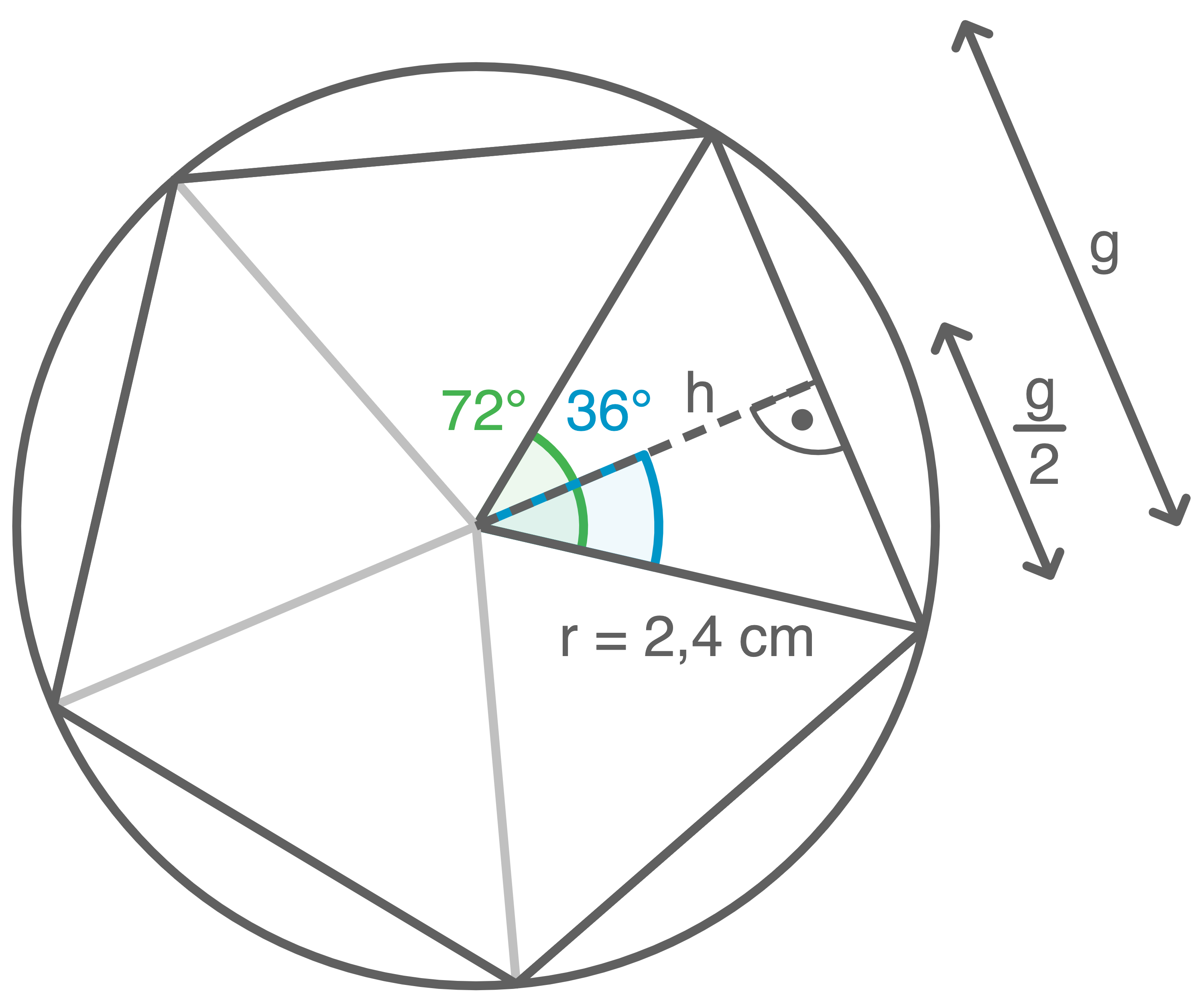 Formel zur Berechnung des Flächeninhalts des Fünfecks:
Formel zur Berechnung des Flächeninhalts des Fünfecks:  Dafür wird zunächst die Höhe
Dafür wird zunächst die Höhe  berechnet:
berechnet:
![\(\begin{array}[t]{rll}
\cos\left(\dfrac{\alpha}{2}\right)&=& \dfrac{h}{r}&\quad \scriptsize \mid\;\cdot r \\[5pt]
\cos\left(\dfrac{\alpha}{2}\right)\cdot r&=& h& \\[5pt]
h&=& \cos\left(\dfrac{\alpha}{2}\right)\cdot r& \\[5pt]
h&=& \cos(36^{\circ})\cdot 2,4\,\text{m}& \\[5pt]
h&\approx& 1,94\,\text{m}
\end{array}\)](https://www.schullv.de/resources/formulas/d3b29004c48b7e1b05583ac845e522fa8de1e7a4230568990f6cc589471eefee_light.svg) Damit kann die Länge von
Damit kann die Länge von  berechnet werden:
berechnet werden:
![\(\begin{array}[t]{rll}
\left(\dfrac{g}{2}\right)^2+h^2&=&r^2 &\scriptsize \mid\;-h^2 \\[5pt]
\left(\dfrac{g}{2}\right)^2&=&r^2-h^2 &\scriptsize \mid\;\sqrt{\,\,} \\[5pt]
\dfrac{g}{2}&=&\sqrt{r^2-h^2} \\[5pt]
\dfrac{g}{2}&=&\sqrt{(2,4\,\text{m})^2-(1,94\,\text{m})^2} \\[5pt]
\dfrac{g}{2}&\approx&1,41\,\text{m}&\scriptsize \mid\;\cdot 2 \\[5pt]
g&=&2,82\,\text{m}
\end{array}\)](https://www.schullv.de/resources/formulas/bf7502cee6d40b6dc79e8d41e5005542dbf389847158d9bdfecd60697a6b7fd3_light.svg) Damit folgt für den Flächeninhalt:
Damit folgt für den Flächeninhalt:
![\(\begin{array}[t]{rll}
A&=& 5\cdot \dfrac{g\cdot h}{2} \\[5pt]
A&=& 5\cdot \dfrac{2,82\,\text{m}\cdot 1,94\,\text{m}}{2} \\[5pt]
A&=& \boldsymbol{13,677\,\text{m}^2}
\end{array}\)](https://www.schullv.de/resources/formulas/63d6611ea88083986f73109059176ee25746c9b181342e9ab9a7489fa396d0df_light.svg)
- Durchmesser in der Abbildung:
- Größe der Person in der Abbildung:

b)
Tabelle für die ersten sechs Monate der Kreditlaufzeit ergänzen
Da Julian bereits  von seinen Eltern bekommen hat, muss er nur noch einen Kredit in Höhe von
von seinen Eltern bekommen hat, muss er nur noch einen Kredit in Höhe von  aufnehmen.
Welcher Betrag des Kredits ist nach 6 Monaten getilgt?
aufnehmen.
Welcher Betrag des Kredits ist nach 6 Monaten getilgt?


c)
Abstand zwischen Punkt  und Punkt
und Punkt  berechnen
Da
berechnen
Da  und
und  die Nullpunkte der Parabel bilden, wird die Funkionsgleichung der Parabel gleich Null gesetzt:
die Nullpunkte der Parabel bilden, wird die Funkionsgleichung der Parabel gleich Null gesetzt:
![\(\begin{array}[t]{rll}
-0,05\cdot(x-20)^2+45&=& 0&\\[5pt]
-0,05\cdot(x^2-40x+400)+45&=& 0& \\[5pt]
-0,05x^2+2x-20+45&=& 0&\\[5pt]
-0,05x^2+2x+25&=& 0& \scriptsize \mid\;:(-0,05) \\[5pt]
x^2-40x-500&=& 0& \\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/424b346cec3e5614d9de7ca0560a4548f6dfbca1750700d1708ca281137ff891_light.svg)
![\(\begin{array}[t]{rll}
x_{1/2}&=& -\dfrac{-40}{2}\pm\sqrt{\left(\dfrac{-40}{2}\right)^2+500}& \\[5pt]
x_{1/2}&=& 20\pm\sqrt{900}& \\[5pt]
x_{1}&=& 20+30=50& \\[5pt]
x_{2}&=& 20-30=-10
\end{array}\)](https://www.schullv.de/resources/formulas/f62905925c4182262caa1afa581b6d8aa7338b52860f898bec50013593cf9cff_light.svg) Daraus folgt:
Daraus folgt:  und
und  Der Abstand zwischen
Der Abstand zwischen  und
und  beträgt
beträgt  Strecke
Strecke  auf der
auf der  -Achse berechnen
Die Strecke
-Achse berechnen
Die Strecke  bildet den vertikalen Abstand zwischen dem Scheitelpunkt der Parabel und ihrem Schnittpunkt mit der
bildet den vertikalen Abstand zwischen dem Scheitelpunkt der Parabel und ihrem Schnittpunkt mit der  -Achse.
Koordinaten des Schnittpunkts mit der
-Achse.
Koordinaten des Schnittpunkts mit der  -Achse bestimmen:
-Achse bestimmen:
![\(\begin{array}[t]{rll}
y&=& -0,05\cdot (x-20)^2+45& \\[5pt]
y&=& -0,05\cdot (0-20)^2+45&\\[5pt]
y&=& -0,05\cdot 20^2+45& \\[5pt]
y&=& -20+45& \\[5pt]
y&=& 25
\end{array}\)](https://www.schullv.de/resources/formulas/05a70a93006025067a318c7b609d34b662cd35468f5f806127882c318d6bfd00_light.svg)
 Koordinaten des Scheitelpunkts der Parabel bestimmen:
Eine Parabel mit
Koordinaten des Scheitelpunkts der Parabel bestimmen:
Eine Parabel mit  hat den Scheitelpunkt
hat den Scheitelpunkt  Somit kann der Scheitelpunkt anhand der Funktionsgleichung
Somit kann der Scheitelpunkt anhand der Funktionsgleichung  abgelesen werden.
abgelesen werden.
 Daraus folgt:
Daraus folgt: 
Lösung 3
a)
Länge von  berechnen
berechnen
![\(\begin{array}[t]{rll}
\tan(\beta)&=&\dfrac{\overline{EF}}{\overline{BE}} &\quad \scriptsize \mid\; \cdot\overline{BE} \\[5pt]
\tan(\beta)\cdot\overline{BE}&=&\overline{EF}& \\[5pt]
\overline{EF}&=&\tan(\beta)\cdot\overline{BE}&\\[5pt]
\overline{EF}&=&\tan(33^{\circ})\cdot3,8\,\text{m} \\[5pt]
\overline{EF}&\approx&\boldsymbol{2,47\,\text{m}}
\end{array}\)](https://www.schullv.de/resources/formulas/dff5a6af58124986d85e2c846792764050aededee148d0a83bd1615a7f31e100_light.svg) Maximale Länge von
Maximale Länge von  berechnen
Länge von
berechnen
Länge von  berechnen
berechnen
![\(\begin{array}[t]{rll}
\tan(\alpha)&=&\dfrac{\overline{DG}}{\overline{AD}} &\quad \scriptsize \mid\;\cdot \overline{AD} \\[5pt]
\tan(\alpha)\cdot \overline{AD}&=&\overline{DG}&\quad \scriptsize \mid\;: \tan(\alpha)\\[5pt]
\overline{AD}&=&\dfrac{\overline{DG}}{\tan(\alpha)}\\[5pt]
\overline{AD}&=&\dfrac{2,2\,\text{m}}{\tan(55^{\circ})}\\[5pt]
\overline{AD}&\approx&1,54\,\text{m}
\end{array}\)](https://www.schullv.de/resources/formulas/4cb170678d700a20043bdbb347e2be9747432e8e4fd0e59a399a3b68d1dc4d9d_light.svg) Länge von
Länge von  berechnen
berechnen
![\(\begin{array}[t]{rll}
\tan(\beta)&=&\dfrac{\overline{EF}}{\overline{BE}} &\quad \scriptsize \mid\;\cdot \overline{BE} \\[5pt]
\tan(\beta)\cdot \overline{BE}&=&\overline{EF} &\quad \scriptsize \mid\;: \tan(\beta)\\[5pt]
\overline{BE}&=&\dfrac{\overline{EF}}{\tan(\beta)} &\\[5pt]
\overline{BE}&=&\dfrac{2,2\,\text{m}}{\tan(33^{\circ})} &\\[5pt]
\overline{BE}&\approx&3,39\,\text{m}
\end{array}\)](https://www.schullv.de/resources/formulas/dadd09bd7f7d58fce77a56c42a2d2f116a71fae434e7f9205eaaa3ddfcbd7146_light.svg) Maximale Länge von
Maximale Länge von  berechnen
berechnen
![\(\begin{array}[t]{rll}
\overline{DE}&=&\overline{AB}-\overline{AD}-\overline{BE}\\[5pt]
\overline{DE}&=&8,5\,\text{m}-1,54\,\text{m}-3,39\,\text{m}\\[5pt]
\overline{DE}&=&\boldsymbol{3,57\,\text{m}}
\end{array}\)](https://www.schullv.de/resources/formulas/5d24d62eba399e18c2353d216150987e2a2ec67dd478d75ab7c9856c350c01b2_light.svg)
b)
Das durchschnittliche jährliche Wachstum in Prozent berechnen
Gegeben:
![\(\begin{array}[t]{rll}
W_n&=& W_0\cdot q^n \\[5pt]
W_5&=& W_0\cdot q^5&\quad \scriptsize \mid\;:W_0 \\[5pt]
\dfrac{W_5}{W_0}&=& q^5\\[5pt]
q^5&=&\dfrac{W_5}{W_0}&\quad \scriptsize \mid\;\sqrt[5]{\,\,} \\[5pt]
q&=&\sqrt[5]{\dfrac{W_5}{W_0}}\\[5pt]
q&=&\sqrt[5]{\dfrac{20\,900\,\text{t}}{6\,600\,\text{t}}}\\[5pt]
q&\approx&1,259
\end{array}\)](https://www.schullv.de/resources/formulas/dbaeb9bf0eaed29f99a938e463e4194ebbce12be20539789736e04b49a5be617_light.svg) Das durchschnittliche Wachstum beträgt:
Das durchschnittliche Wachstum beträgt:

 Wie viele Kapseln werden im Jahr 2018 verkauft?
Kaffee im Jahr 2018 in Tonnen berechnen
Gegeben:
Wie viele Kapseln werden im Jahr 2018 verkauft?
Kaffee im Jahr 2018 in Tonnen berechnen
Gegeben:
![\(\begin{array}[t]{rll}
W_n&=& W_0\cdot \left(1+\dfrac{p}{100}\right)^n\\[5pt]
W_3&=& 20\,900\,\text{t}\cdot \left(1+\dfrac{23}{100}\right)^3\\[5pt]
W_3&\approx& 38\,892,12\,\text{t}
\end{array}\)](https://www.schullv.de/resources/formulas/284bc0ac03685794b42ed18e1686bd19bd9117ba2f6d6ca38db4a75dfbc9ddaa_light.svg) Anzahl der Kaffee-Kapseln im Jahr 2018 berechnen
Anzahl der Kaffee-Kapseln im Jahr 2018 berechnen

 Im Jahr 2018 wurden
Im Jahr 2018 wurden  Kaffee-Kapseln verkauft.
Kaffee-Kapseln verkauft.
Kaffee
Jahre
Kaffee
Kaffee
Jahre
c)
Neue Funktionsgleichung angeben
 Rechnerisch überprüfen, ob die Gerade die abgebildete Parabel schneidet
Rechnerisch überprüfen, ob die Gerade die abgebildete Parabel schneidet
![\(\begin{array}[t]{rll}
(x-1,5)^2+1&=& -4x+7 \\[5pt]
x^2-3x+2,25+1&=& -4x+7\\[5pt]
x^2-3x+3,25&=& -4x+7&\quad \scriptsize \mid\;+4x \\[5pt]
x^2+x+3,25&=&7&\quad \scriptsize \mid\;-7 \\[5pt]
x^2+x-3,75&=&0\\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/109ce930b6ccba4b5cf696b7168653109c3040397e29281baeafc341878b9ee7_light.svg)
![\(\begin{array}[t]{rll}
x_{1/2}&=&-\dfrac{1}{2}\pm\sqrt{\left(\dfrac{1}{2}\right)^2+3,75}\\[5pt]
x_{1/2}&=&-0,5\pm\sqrt{4}\\[5pt]
x_{1}&=&-0,5+2=1,5\\[5pt]
x_{2}&=&-0,5-2=-2,5
\end{array}\)](https://www.schullv.de/resources/formulas/5a8e13df4dd6533ca26a415752375b278bc5076b0a0f4f7fca708eab50bc7759_light.svg) Somit schneiden sich die Gerade und die Parabel: Einmal an der Stelle
Somit schneiden sich die Gerade und die Parabel: Einmal an der Stelle  und an der Stelle
und an der Stelle  Um die Schnittpunkte zu bestimmen, muss noch jeweils die
Um die Schnittpunkte zu bestimmen, muss noch jeweils die  -Koordinate berechnet werden:
-Koordinate berechnet werden:
![\(\begin{array}[t]{rll}
y_1&=&-4\cdot x_1+7 \\[5pt]
y_1&=&-4\cdot 1,5+7 \\[5pt]
y_1&=&1
\end{array}\)](https://www.schullv.de/resources/formulas/4df643931d78d6c68a19f2f02ff65c27d72c02aaf017ed248181ad52d393fe2e_light.svg)

![\(\begin{array}[t]{rll}
y_2&=&-4\cdot x_1+7 \\[5pt]
y_2&=&-4\cdot (-2,5)+7 \\[5pt]
y_2&=&17
\end{array}\)](https://www.schullv.de/resources/formulas/46df39749cf5a6be55099b8877feaeab9b4a6cb739e458387eb4c31e8c415259_light.svg)

Lösung 4
a)
Wert der Insel im Jahr 2018 bestimmmen
Gegeben:
![\(\begin{array}[t]{rll}
W_n&=&W_0\cdot \left(1+\dfrac{p}{100}\right)^n \\[5pt]
W_{392}&=&24\,\text{Dollar}\cdot \left(1+\dfrac{5}{100}\right)^{392} \\[5pt]
W_{392}&=&4\,857\,541\,024 \\[5pt]
W_{392}&\approx&\boldsymbol{4,858\,\text{Mrd. Dollar}}
\end{array}\)](https://www.schullv.de/resources/formulas/d7e59de7540213fe667b4d02ccdd5976153f82fa7c440c213014405bd4ed72a5_light.svg) In welchem Zeitabschnitt war die prozentuale Zunahme der Bevölkerung am größten?
Formel zur Berechnung der prozentualen Zunahme:
In welchem Zeitabschnitt war die prozentuale Zunahme der Bevölkerung am größten?
Formel zur Berechnung der prozentualen Zunahme:  1800 - 1850
1800 - 1850

Jahre
- Absolute Zunahme:
- Prozentuale Zunahme:
- Absolute Zunahme:
- Prozentuale Zunahme:
- Absolute Zunahme:
- Prozentuale Zunahme:
- Absolute Zunahme:
- Prozentuale Zunahme:
b)
Wie viele unterschiedliche Kombinationen gibt es, bei denen eine Zahl genau zweimal vorkommt?
Es gibt 18 unterschiedliche Kombinationen.
Höhe  der quadratischen Pyramide berechnen
der quadratischen Pyramide berechnen
![\(\begin{array}[t]{rll}
V&=& \dfrac{1}{3}\cdot G\cdot h& \\[5pt]
V&=& \dfrac{1}{3}\cdot a^2\cdot h& \\[5pt]
V&=& \dfrac{1}{3}\cdot (2h)^2\cdot h& \\[5pt]
V&=& \dfrac{1}{3}\cdot 4h^2\cdot h& \\[5pt]
V&=& \dfrac{1}{3}\cdot 4h^3&\\[5pt]
V&=& \dfrac{4}{3}\cdot h^3&\quad \scriptsize \mid\;\cdot \dfrac{3}{4} \\[5pt]
\dfrac{3}{4} \cdot V&=& h^3&\\[5pt]
h^3&=&\dfrac{3}{4} \cdot V&\quad \scriptsize \mid\;\sqrt[3]{\,\,} \\[5pt]
h&=&\sqrt[3]{\dfrac{3}{4} \cdot V}& \\[5pt]
h&=&\sqrt[3]{\dfrac{3}{4}\cdot 1\,755\,\text{cm}^3} & \\[5pt]
h&\approx&11\,\text{cm}
\end{array}\)](https://www.schullv.de/resources/formulas/5469418becb96167502abedc88727fbfd6650762db593a59d673abc524e9ae48_light.svg) Die Höhe der Pyramide beträgt ca.
Die Höhe der Pyramide beträgt ca. 
| 1 doppelt | 2 doppelt | 3 doppelt |
|---|---|---|
c)
Streckenlänge zwischen der Tal- und der Mittelstation berechnen
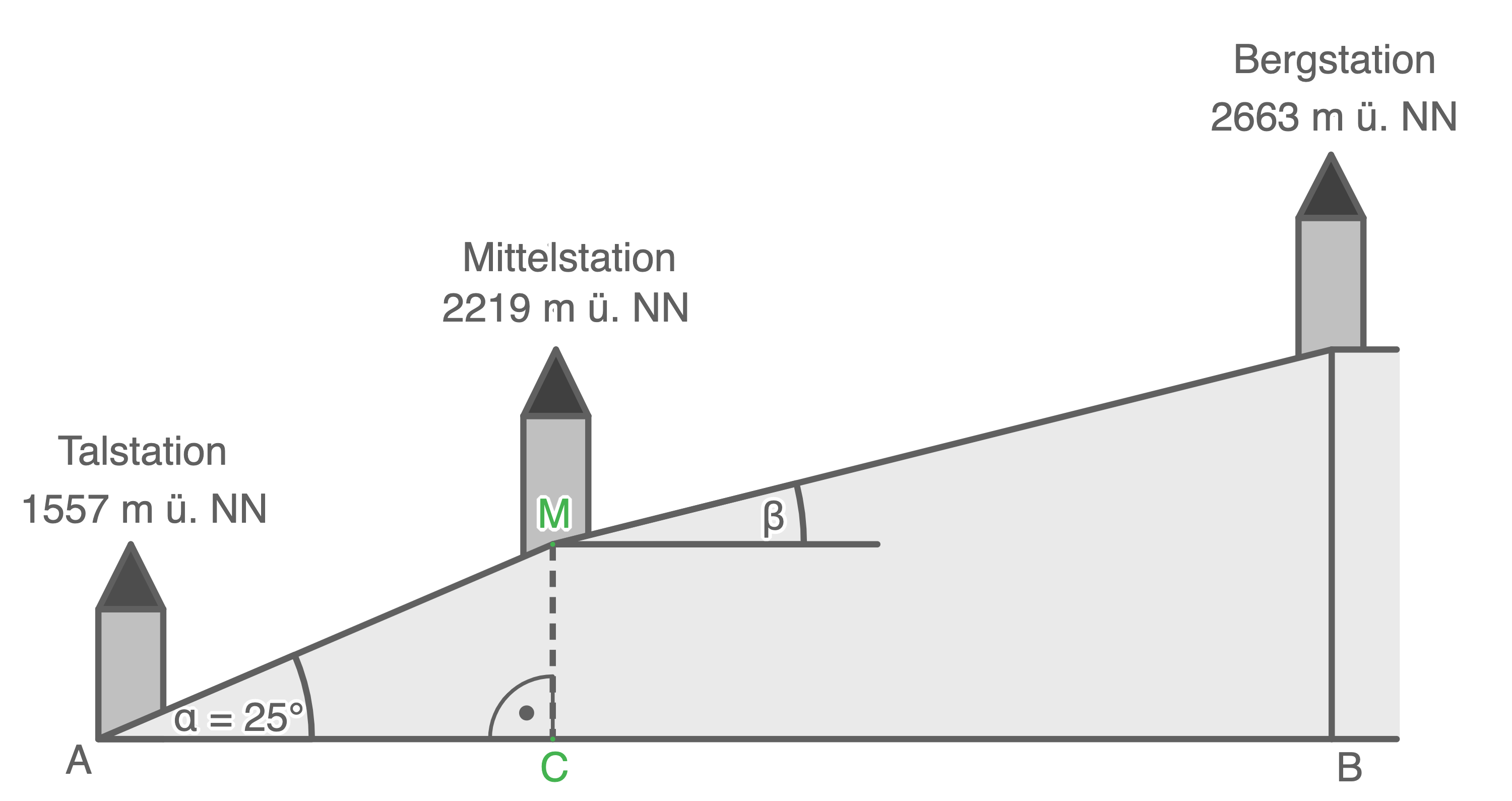 Streckenlänge von
Streckenlänge von  berechnen
berechnen
 Streckenlänge von
Streckenlänge von  berechnen
berechnen
![\(\begin{array}[t]{rll}
\sin(\alpha)&=& \dfrac{\overline{CM}}{\overline{AM}}&\quad \scriptsize \mid\;\cdot \overline{AM} \\[5pt]
\sin(\alpha)\cdot \overline{AM}&=&\overline{CM}&\quad \scriptsize \mid\;:\sin(\alpha)\\[5pt]
\overline{AM}&=&\dfrac{\overline{CM}}{\sin(\alpha)}&\\[5pt]
\overline{AM}&=&\dfrac{662\,\text{m}}{\sin(25^{\circ})}&\\[5pt]
\overline{AM}&\approx&\boldsymbol{1\,566\,\text{m}}
\end{array}\)](https://www.schullv.de/resources/formulas/9e5e2ac6264b293267c62cb2f1f4541a54702b45c91f3a6e068542b284b9df24_light.svg) Größe des Winkels
Größe des Winkels  berechnen
berechnen
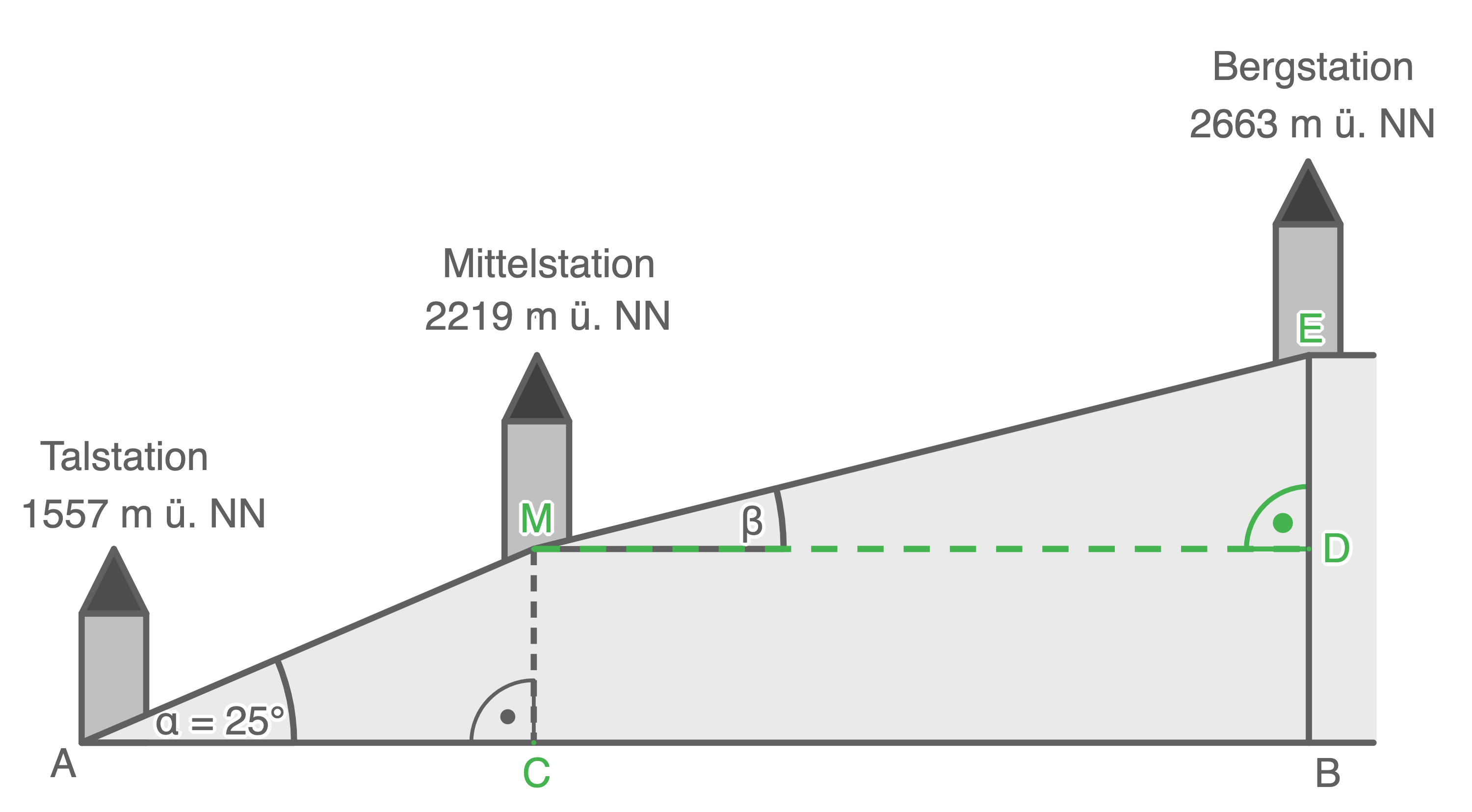 Streckenlänge von
Streckenlänge von  berechnen
berechnen
 Größe des Winkels
Größe des Winkels  berechnen
berechnen
![\(\begin{array}[t]{rll}
\sin(\beta)&=&\dfrac{\overline{DE}}{\overline{ME}} \\[5pt]
\sin(\beta)&=&\dfrac{444\,\text{m}}{2\,188\,\text{m}} \\[5pt]
\sin(\beta)&\approx&0,2029&\quad \scriptsize \mid\;\sin^{-1} \\[5pt]
\beta&\approx&\boldsymbol{11,7^{\circ}}
\end{array}\)](https://www.schullv.de/resources/formulas/9deec503fe5e631da4403ff19394b6242e1dc619a5553257f55a5f6a442cd1d6_light.svg) Abstand
Abstand  berechnen
Streckenlänge von
berechnen
Streckenlänge von  berechnen
berechnen
![\(\begin{array}[t]{rll}
\overline{AC}^2+\overline{CM}^2&=& \overline{AM}^2\quad\quad\quad\quad\quad\quad\quad \scriptsize \mid\;-\overline{CM}^2 \\[5pt]
\overline{AC}^2&=& \overline{AM}^2-\overline{CM}^2 \quad\quad\quad\scriptsize \mid\;\sqrt{\,\,}\\[5pt]
\overline{AC}&=& \sqrt{(1\,566\,\text{m})^2-(662\,\text{m})^2}\\[5pt]
\overline{AC}&\approx& 1\,419,19\,\text{m}
\end{array}\)](https://www.schullv.de/resources/formulas/5574195d7e151e5ff36c2870445cd39c538123540719350746739c8af9cdbc58_light.svg) Streckenlänge von
Streckenlänge von  berechnen
berechnen
![\(\begin{array}[t]{rll}
\overline{MD}^2+\overline{DE}^2&=& \overline{ME}^2&\scriptsize \mid\; -\overline{DE}^2\\[5pt]
\overline{MD}^2&=& \overline{ME}^2-\overline{DE}^2&\scriptsize \mid\;\sqrt{\,\,}\\[5pt]
\overline{MD}&=& \sqrt{\overline{ME}^2-\overline{DE}^2}\\[5pt]
\overline{MD}&=& \sqrt{2\,188\,\text{m}^2-444\,\text{m}^2}\\[5pt]
\overline{MD}&\approx& 2\,142,48\,\text{m}
\end{array}\)](https://www.schullv.de/resources/formulas/e9a35e389b1d22385b21640958147b09547f98f336a36b80a269271a02bd5671_light.svg) Abstand von
Abstand von  berechnen
berechnen
![\(\begin{array}[t]{rll}
\overline{AB}&=&\overline{AC}+\overline{BC} \\[5pt]
\overline{AB}&=&1\,419,19\,\text{m}+2\,142,48\,\text{m} \\[5pt]
\overline{AB}&=&\boldsymbol{3\,561,67\,\text{m}}
\end{array}\)](https://www.schullv.de/resources/formulas/67ebfd4015056fbf047dae69bb10bc5822e93ef63052fcada2e007b34f18db72_light.svg)

