Grundkenntnisse
1.
Löse die Gleichung.

(1 Pkt.)
2.
Löse das Gleichungssystem.

(1 Pkt.)
3.
Berechne die Höhe 
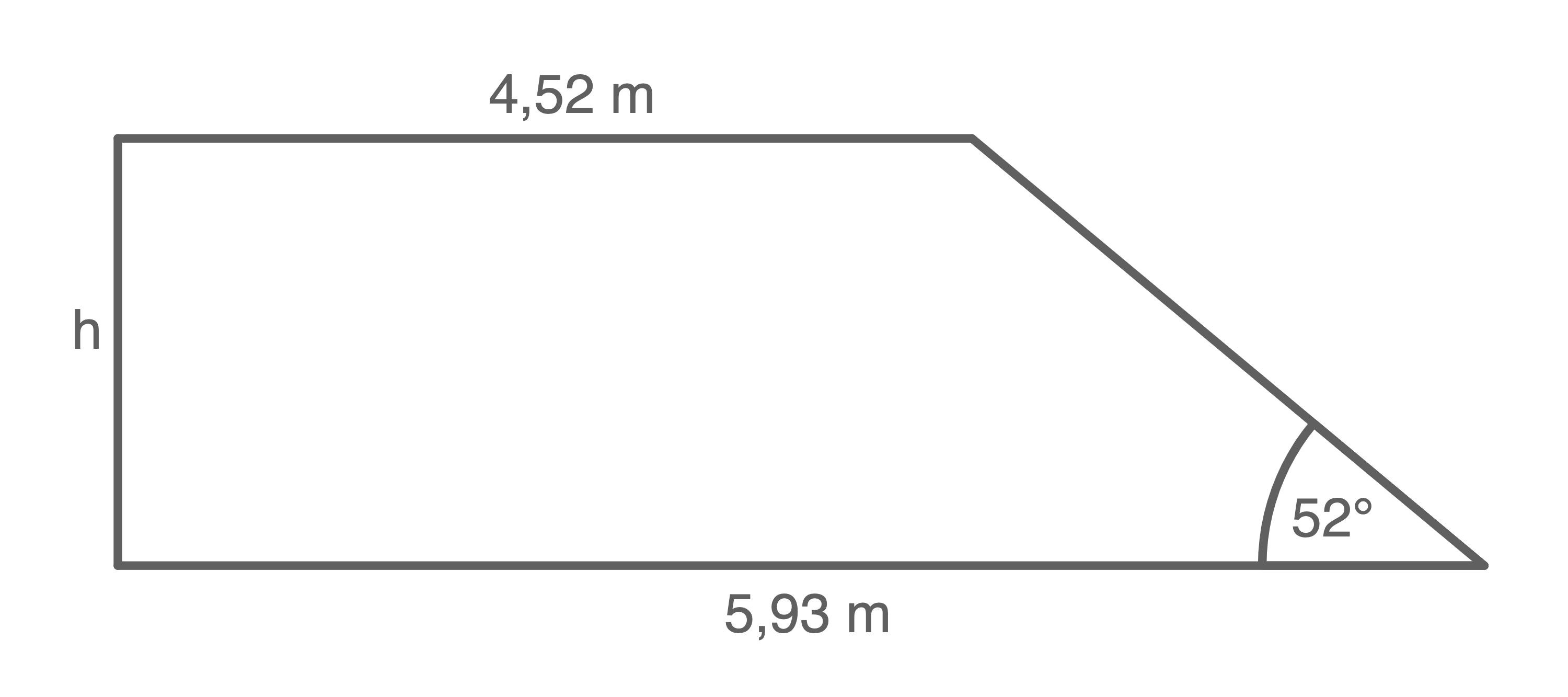

(Skizze nicht maßstabsgetreu)
(1 Pkt.)
4.
Ein Basketball für den Profibereich hat ein Volumen von  .
.
Berechne den Durchmesser des Balls. Betrachte den Ball als Kugel.
Berechne den Durchmesser des Balls. Betrachte den Ball als Kugel.
(1 Pkt.)
5.
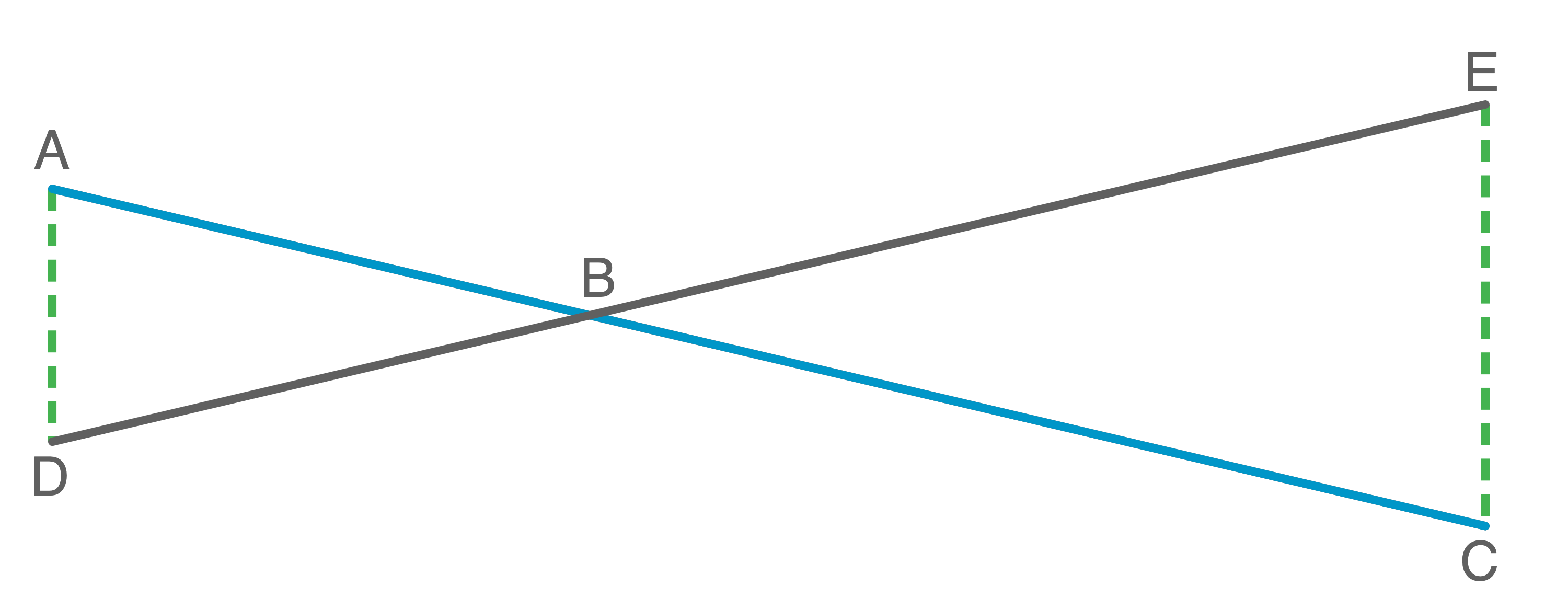
Berechne die Strecke  .
.
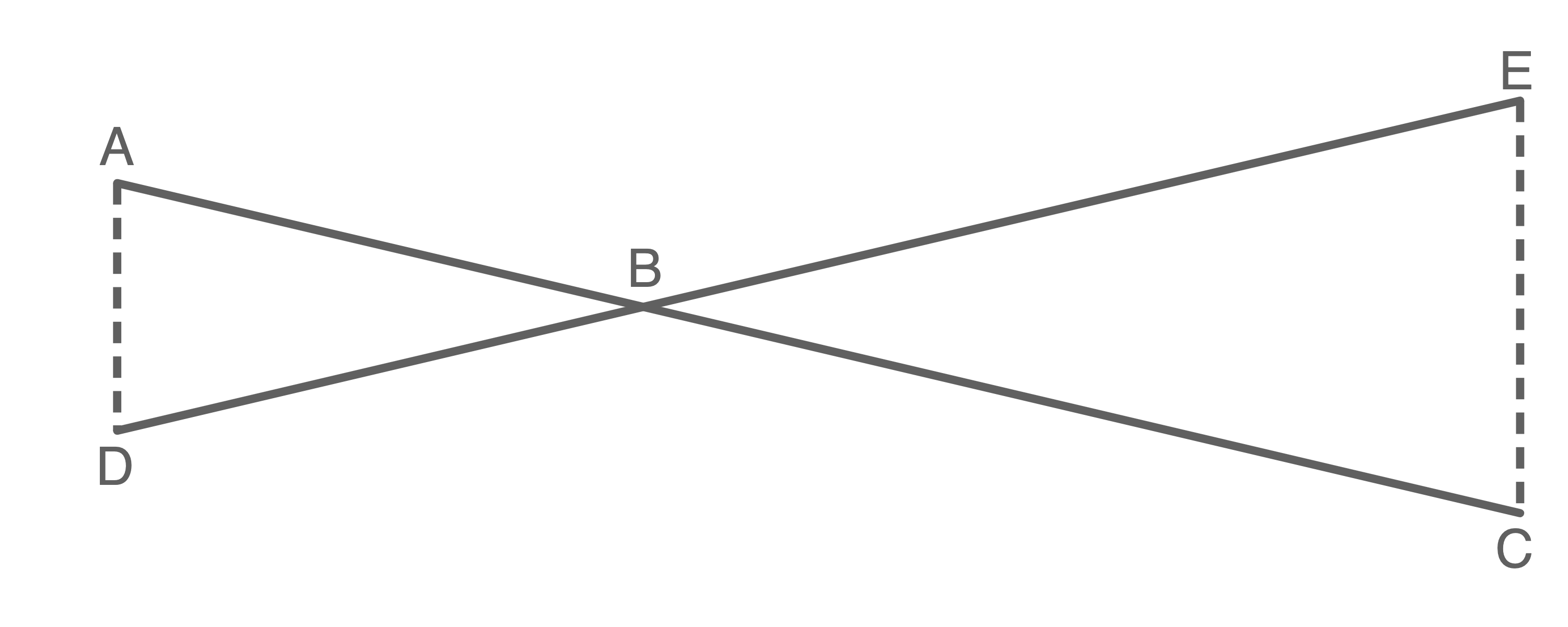





(Skizze nicht maßstabsgetreu)
(1 Pkt.)
6.
Ein Vollgummiball wird in einer Höhe von  fallen gelassen. Nach jedem Aufprall verringert sich die Sprunghöhe um
fallen gelassen. Nach jedem Aufprall verringert sich die Sprunghöhe um  .
Berechne die Sprunghöhe des Balls nach dem zwölften Aufprall.
.
Berechne die Sprunghöhe des Balls nach dem zwölften Aufprall.
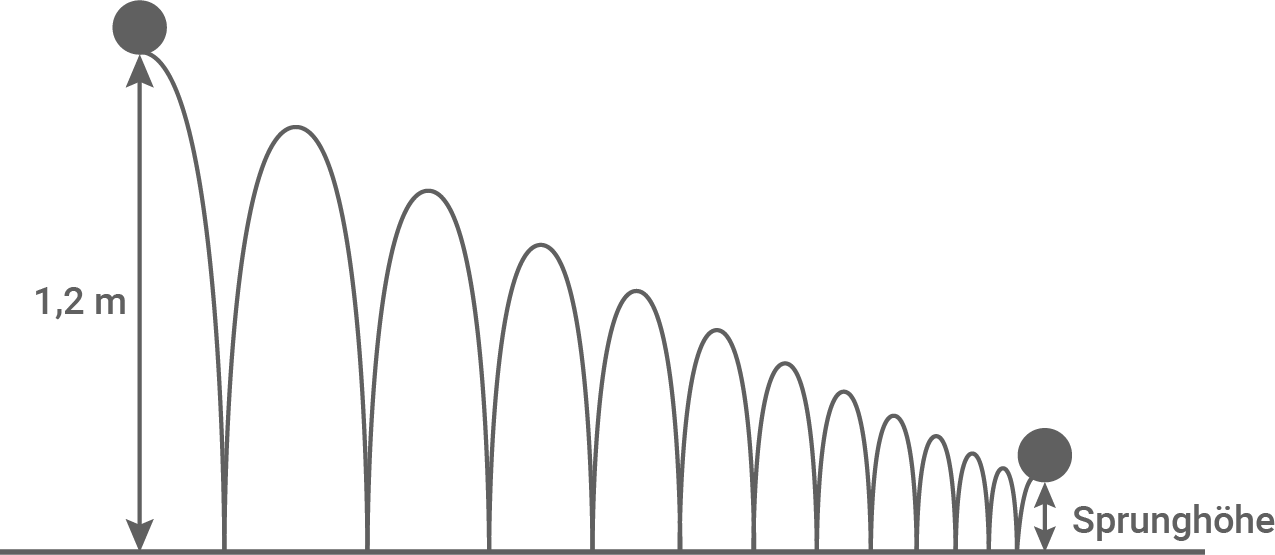

(Skizze nicht maßstabsgetreu)
(1 Pkt.)
7.
Die Parabel  wird um
wird um  Längeneinheiten nach links verschoben.
Bestimme die Funktionsgleichung der verschobenen Parabel.
Längeneinheiten nach links verschoben.
Bestimme die Funktionsgleichung der verschobenen Parabel.
(1 Pkt.)
8.
Gib an, welches der Angebote A bis D im Diagramm dargestellt ist.
A: 
B:
C:
D:
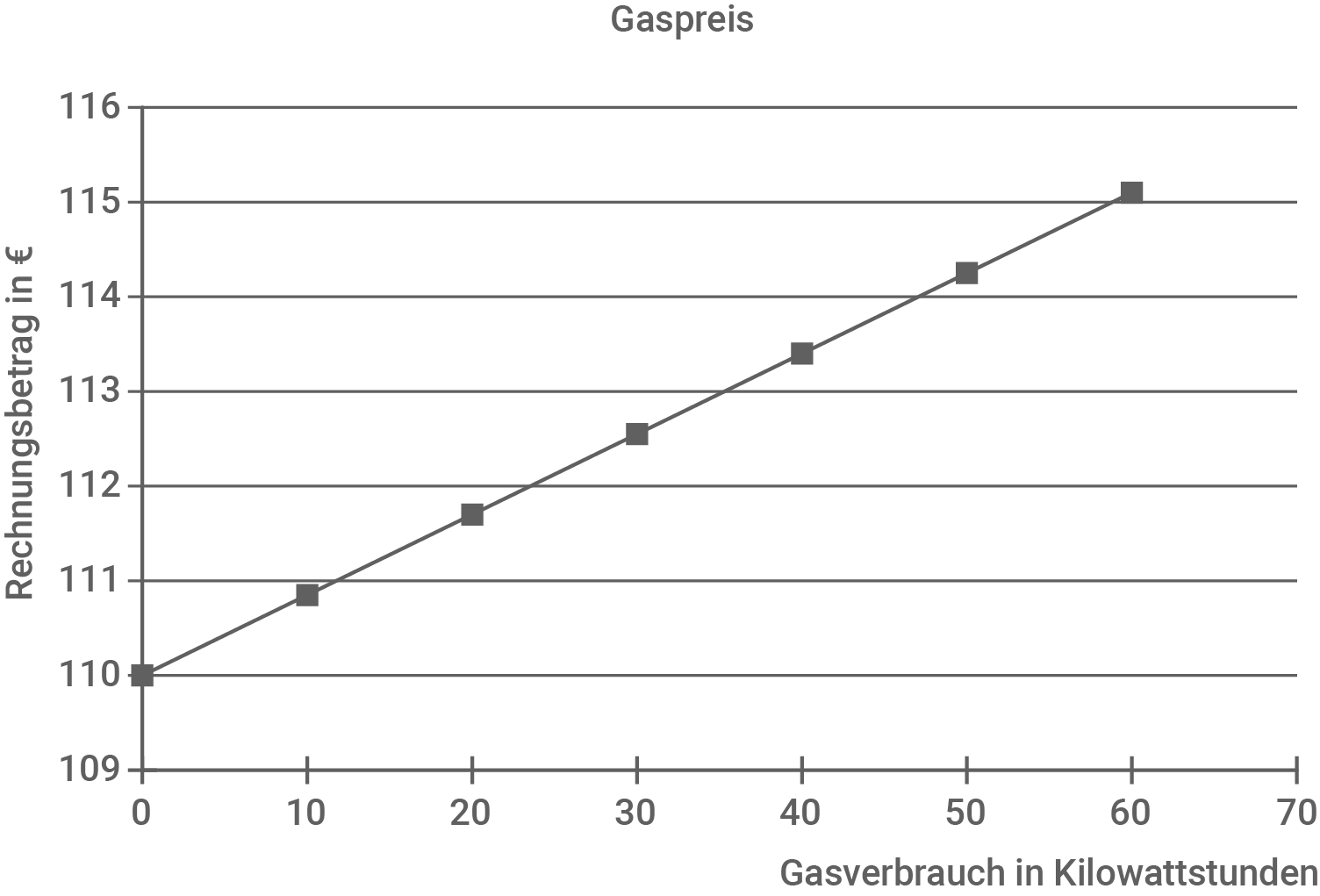
B:
C:
D:

(1 Pkt.)
9.
In einem Beutel befinden sich sechsunddreißig  -Euro-Münzen.
-Euro-Münzen.  Münzen haben die deutsche Prägung,
Münzen haben die deutsche Prägung,  die französische Prägung, die restlichen die spanische Prägung.
Zwei Münzen werden nacheinander ohne Hinschauen und ohne Zurücklegen gezogen.
Berechne die Wahrscheinlichkeit, dass keine Münze mit deutscher Prägung gezogen wird.
die französische Prägung, die restlichen die spanische Prägung.
Zwei Münzen werden nacheinander ohne Hinschauen und ohne Zurücklegen gezogen.
Berechne die Wahrscheinlichkeit, dass keine Münze mit deutscher Prägung gezogen wird.
(1 Pkt.)
10.
Der Landtag von Baden-Württemberg setzt sich aus  Abgeordneten zusammen, davon sind
Abgeordneten zusammen, davon sind  Abgeordnete von den GRÜNEN,
Abgeordnete von den GRÜNEN,  von der CDU,
von der CDU,  von der AfD,
von der AfD,  von der SPD,
von der SPD,  von der FDP/DVP und
von der FDP/DVP und  Abgeordnete sind fraktionslos.
Abgeordnete sind fraktionslos.
(Stand 01.01.2017) Wähle das zutreffende Diagramm aus und begründe deine Entscheidung.
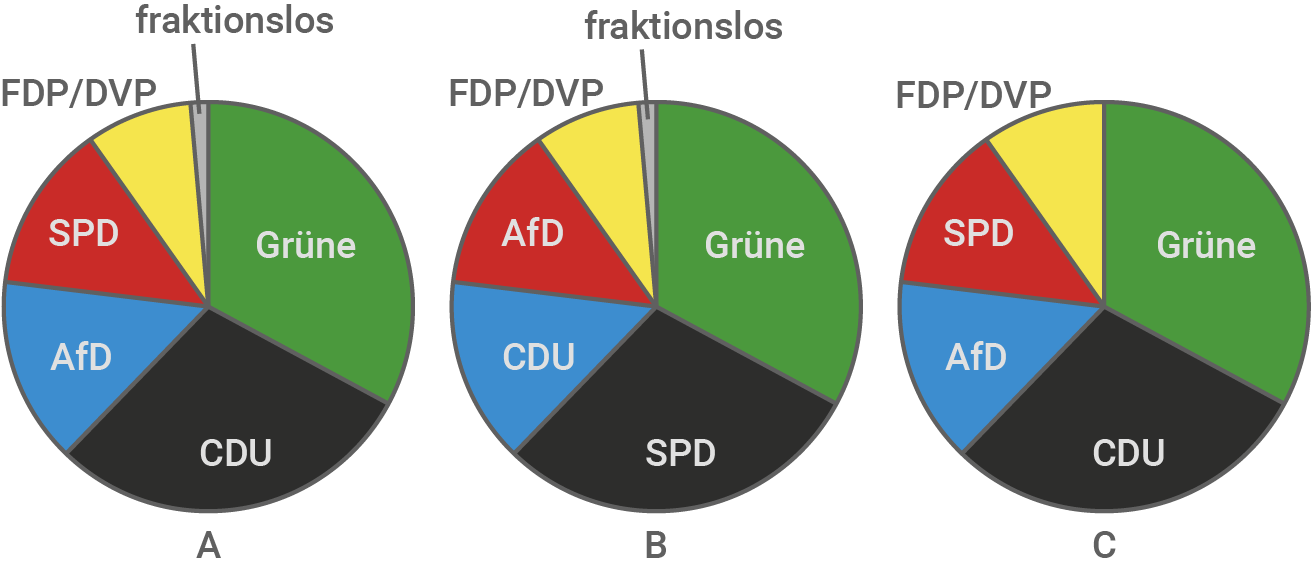
(Stand 01.01.2017) Wähle das zutreffende Diagramm aus und begründe deine Entscheidung.

(1 Pkt.)
1.
2.
Lösung über das Einsetzungsverfahren
Gleichung  nach
nach  auflösen
auflösen
![\(\begin{array}[t]{rll}
\text{(I)}\quad&4y&=& 8x-22 &\quad \scriptsize \mid\;:4 \\[5pt]
\text{(I](https://www.schullv.de/resources/formulas/af4ecb551024ff783ab814a15f025f597fa5eb62edec4d46097ccc451117f4af_light.svg) Gleichung
Gleichung  in Gleichung
in Gleichung  einsetzen
einsetzen
![\(\begin{array}[t]{rll}
6,5&=&y-0,5x \\[5pt]
6,5&=&(2x-5,5)-0,5x \\[5pt]
6,5&=&1,5x-5,5 &\quad \scriptsize \mid\;+5,5 \\[5pt]
12&=&1,5x&\quad \scriptsize \mid\;:1,5 \\[5pt]
\boldsymbol{x}&=& \boldsymbol{8}
\end{array}\)](https://www.schullv.de/resources/formulas/889622a0a0b9395346d47538c1550adb74ca1a804fcff7804b068adb6f6cd281_light.svg)
 in Gleichung
in Gleichung  einsetzen
einsetzen
![\(\begin{array}[t]{rll}
y&=& 2x-5,5 \\[5pt]
y&=& 2\cdot 8-5,5 \\[5pt]
\boldsymbol{y}&=& \boldsymbol{10,5}
\end{array}\)](https://www.schullv.de/resources/formulas/2f9a13920278a7e681973923a061d229741eb252000e3a3840c4b7c8c6b5bf88_light.svg)
Lösung über das Gleichsetzungsverfahren
Gleichung  nach
nach  auflösen
auflösen
![\(\begin{array}[t]{rll}
\text{(I)}\quad&4y&=& 8x-22 &\quad \scriptsize \mid\;:4 \\[5pt]
\text{(I](https://www.schullv.de/resources/formulas/af4ecb551024ff783ab814a15f025f597fa5eb62edec4d46097ccc451117f4af_light.svg) Gleichung
Gleichung  nach
nach  auflösen
auflösen
![\(\begin{array}[t]{rll}
\text{(II)}\quad&6,5&=&y-0,5x &\quad \scriptsize \mid\;+0,5x \\[5pt]
\text{(II](https://www.schullv.de/resources/formulas/5fc61e97416fc956b8f374aa6afdfe5615ca587cb560850e269ffe0609a4ae53_light.svg) Gleichung
Gleichung  und
und  gleichsetzen
gleichsetzen
![\(\begin{array}[t]{rll}
2x-5,5 &=& 6,5+0,5x&\quad \scriptsize \mid\;+5,5 \\[5pt]
2x &=& 12+0,5x&\quad \scriptsize \mid\;-0,5x \\[5pt]
1,5x &=& 12&\quad \scriptsize \mid\;:1,5\\[5pt]
\boldsymbol{x}&=& \boldsymbol{8}
\end{array}\)](https://www.schullv.de/resources/formulas/78ac40077f4e2e410af9316e76573bc434728f518ee94b24cd902c8a973a3bef_light.svg)
 in Gleichung
in Gleichung  einsetzen
einsetzen
![\(\begin{array}[t]{rll}
y&=& 2x-5,5 \\[5pt]
y&=& 2\cdot 8-5,5 \\[5pt]
\boldsymbol{y}&=& \boldsymbol{10,5}
\end{array}\)](https://www.schullv.de/resources/formulas/2f9a13920278a7e681973923a061d229741eb252000e3a3840c4b7c8c6b5bf88_light.svg)
3.
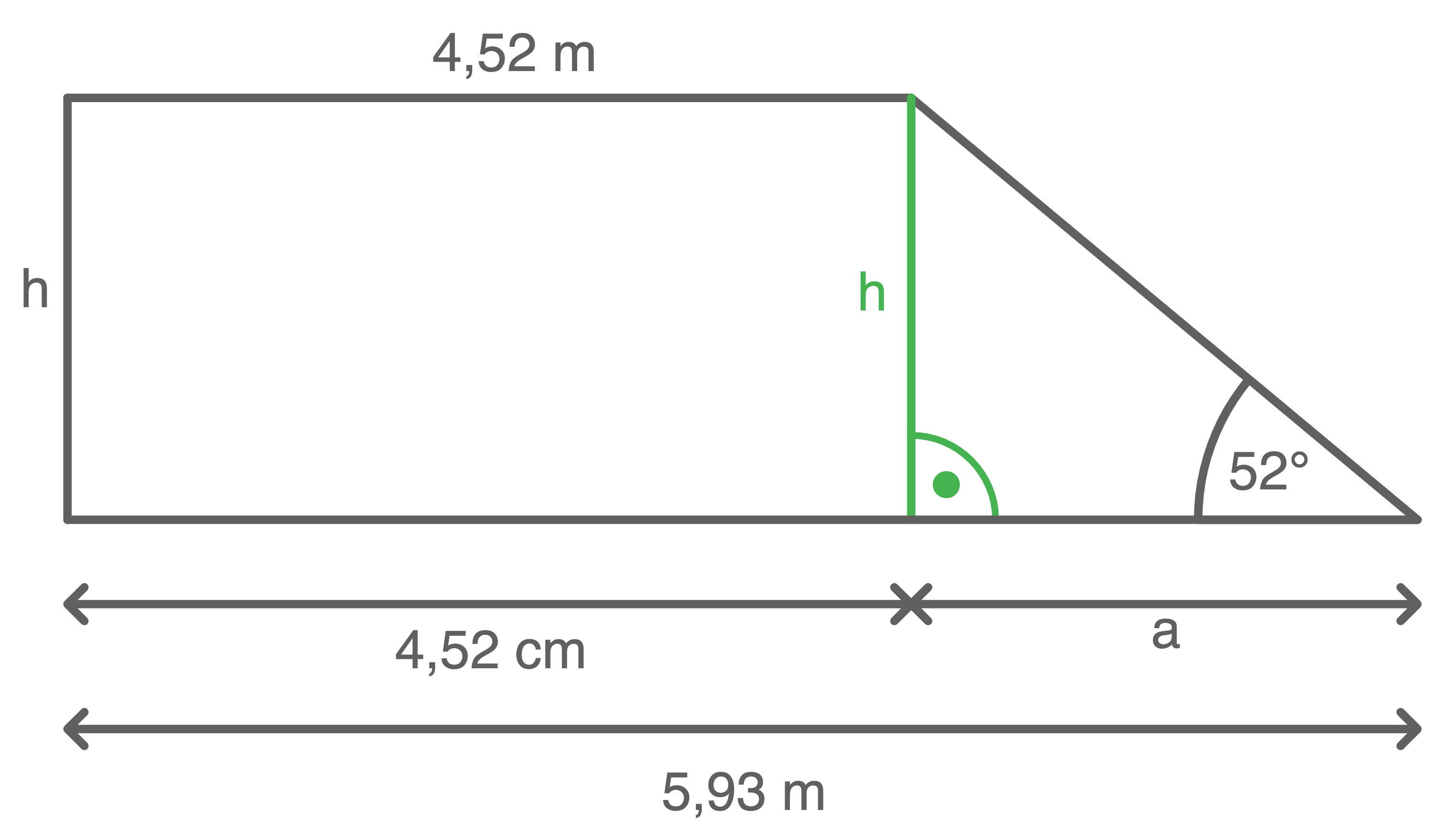
Länge von
4.
Um den Durchmesser zu berechnen, wird die Formel zur Berechnung des Volumens einer Kugel nach  umgestellt:
umgestellt:
![\(\begin{array}[t]{rll}
V&=&\dfrac{4}{3}\cdot \pi\cdot r^3 &\quad \scriptsize \mid\;\cdot \dfrac{3}{4} \\[5pt]
\dfrac{3}{4}\cdot V&=& \pi\cdot r^3 &\quad \scriptsize \mid\;:\pi \\[5pt]
\dfrac{3}{4}\cdot \dfrac{V}{\pi}&=& r^3 \\[5pt]
r^3&=& \dfrac{3}{4}\cdot \dfrac{V}{\pi}&\quad \scriptsize \mid\;\sqrt[3]{\,\,} \\[5pt]
r&=& \sqrt[3]{\dfrac{3}{4}\cdot \dfrac{V}{\pi}} \\[5pt]
r&=& \sqrt[3]{\dfrac{3}{4}\cdot \dfrac{7\,238,23\,\text{cm}^3}{\pi}} \\[5pt]
r&\approx& 12,0\,\text{cm}
\end{array}\)](https://www.schullv.de/resources/formulas/270693ff14c0f0953d45f8b9e68609823edb03c03ff286192a81ee46060cc9f4_light.svg) Daraus folgt für den Durchmesser:
Daraus folgt für den Durchmesser: 
5.
Mit dem 2. Strahlensatz die Länge von  berechnen:
berechnen:
![\(\begin{array}[t]{rll}
\dfrac{\overline{CE}}{\overline{AD}}&=& \dfrac{\overline{BC}}{\overline{AB}}&\quad \scriptsize \mid\; \cdot \overline{AB}\\[5pt]
\dfrac{\overline{CE}}{\overline{AD}}\cdot \overline{AB}&=& \overline{BC}\\[5pt]
\overline{BC}&=&\dfrac{\overline{CE}}{\overline{AD}}\cdot \overline{AB}\\[5pt]
\overline{BC}&=&\dfrac{0,96\,\text{m}}{0,80\,\text{m}}\cdot 1,20\,\text{m}\\[5pt]
\overline{BC}&=&1,44\,\text{m}\\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/05b64cdc7a8f1f7a4da3bdb24fcab49a2c6b63620fbe167aaec0beb7a9d8a411_light.svg) Damit kann nun die Länge von
Damit kann nun die Länge von  berechnet werden:
berechnet werden:
![\(\begin{array}[t]{rll}
\overline{AC}&=&\overline{AB}+\overline{BC} \\[5pt]
\overline{AC}&=&1,20\,\text{m}+1,44\,\text{m} \\[5pt]
\overline{AC}&=&\boldsymbol{2,64\,\text{m}}
\end{array}\)](https://www.schullv.de/resources/formulas/cbf443ce5d5e0fe4ddd6aa8f761678fa4f8e9cb043b205e3a05bf6f2d1ed155e_light.svg)

6.
Gegeben:
![\(\begin{array}[t]{rll}
W_n&=&W_0\cdot \left(1-\dfrac{p}{100}\right)^n \\[5pt]
W_{12}&=&1,2\,\text{m}\cdot \left(1-\dfrac{15}{100}\right)^{12} \\[5pt]
W_{12}&\approx&\boldsymbol{0,17\,\text{m}}
\end{array}\)](https://www.schullv.de/resources/formulas/a2349ba623bf4b287fd653b14780902298ba6e66dd8a2e5382976e2bd7defd48_light.svg) Die Sprunghöhe des Balls nach dem zwölften Aufprall beträgt
Die Sprunghöhe des Balls nach dem zwölften Aufprall beträgt 
7.
8.
Angebot C
9.
Anzahl der Münzen mit spanischer Prägung:  Für einen besseren Überblick hilft das Erstellen eines Baumdiagramms:
Für einen besseren Überblick hilft das Erstellen eines Baumdiagramms:
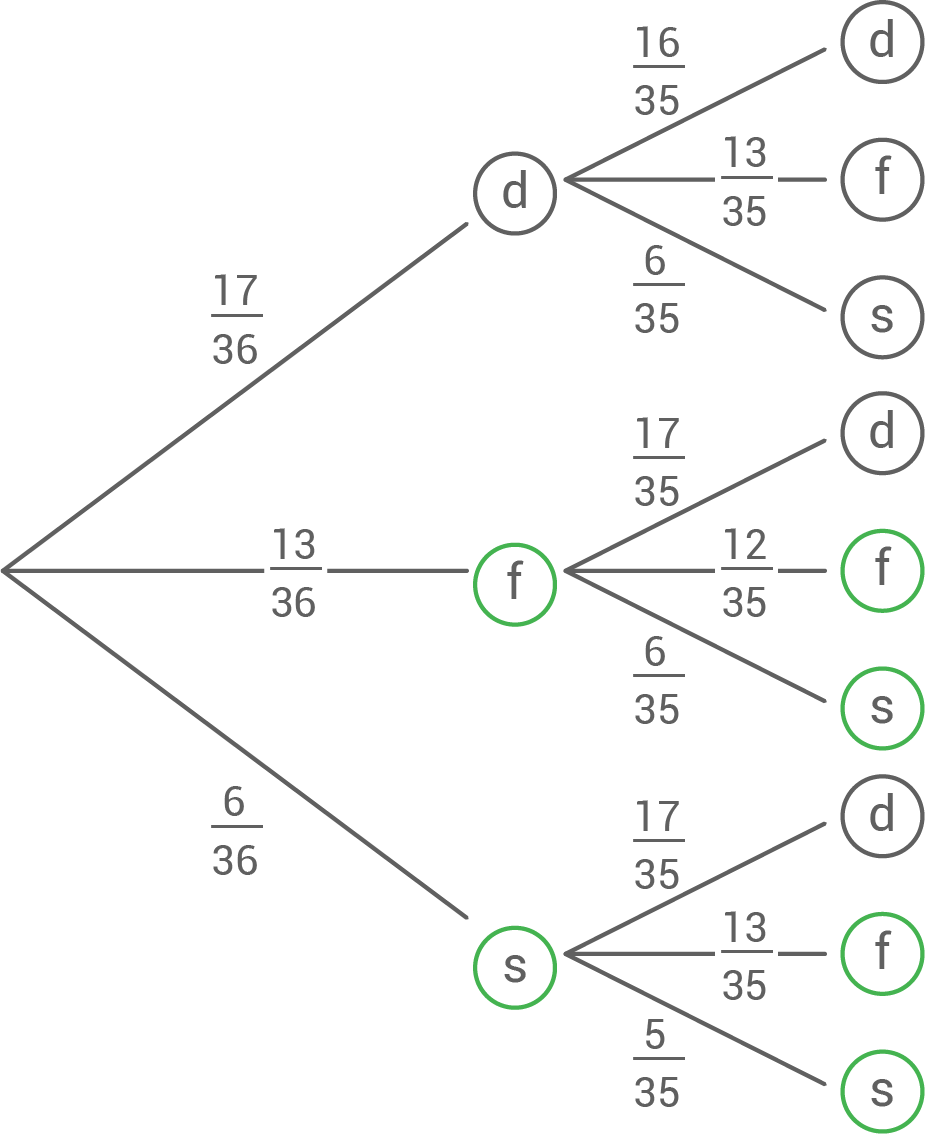 Damit lässt sich die Wahrscheinlichkeit berechnen, dass keine Münze mit deutscher Prägung gezogen wird
Damit lässt sich die Wahrscheinlichkeit berechnen, dass keine Münze mit deutscher Prägung gezogen wird  :
:

10.
Diagramm A
Begründung
- Diagramm B ist nicht zutreffend, da hier die SPD-Fraktion größer ist als die CDU-Fraktion.
- Diagramm C ist auch nicht zutreffend, da hier die fraktionslosen Abgeordneten fehlen.