Grundkenntnisse
1.
Löse die Gleichung.
(1 Pkt.)
2.
Löse das Gleichungssystem.
(1 Pkt.)
3.
Eine Person hält eine 
-Euro-Münze 
im Abstand von 
vor das Auge.
Die Münze deckt einen
hohen Baum vollständig ab.
Berechne die Entfernung der Baumspitze 
vom Auge.
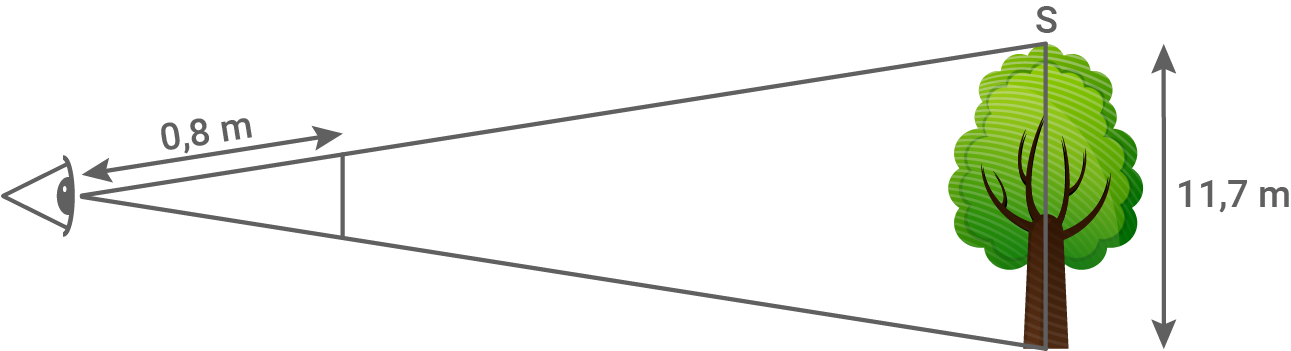
Die Münze deckt einen
(Skizze nicht maßstabsgetreu)
(1 Pkt.)
4.
Ein Eishockeyspieler schießt den Puck in einem Winkel von 
so in das Tor, dass er 
unter der Querstange einschlägt.
Berechne den Abstand 
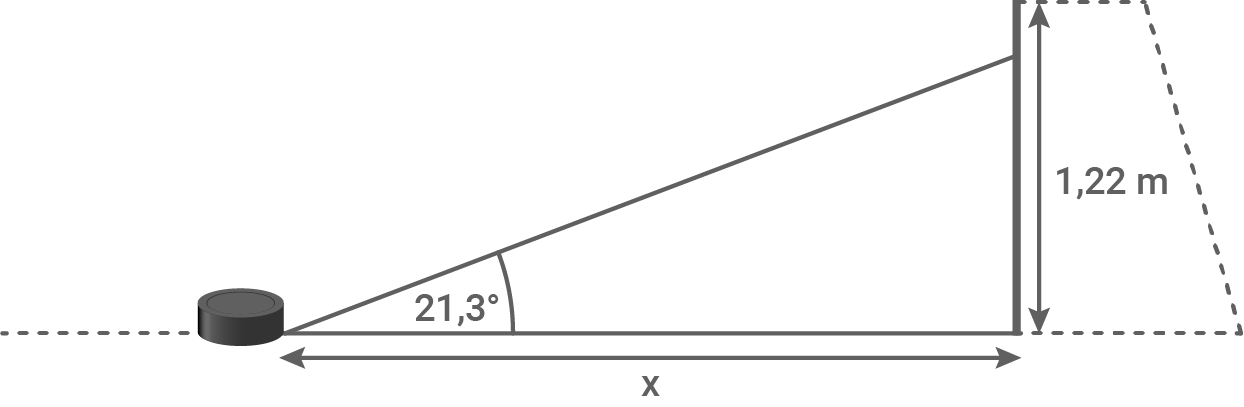
(Skizze nicht maßstabsgetreu)
(1 Pkt.)
5.
Eine Glaskugel hat ein Volumen von 
Sie wird in den kleinstmöglichen zylinderförmigen Karton verpackt.
Berechne den Innenradius und die Innenhöhe des Zylinders.
(1 Pkt.)
6.
Eine Reise kostet 
Überprüfe, ob die Reise von gespartem Geld bezahlt werden kann, wenn man
für 
Jahre zu einem Zinssatz von 
anlegt. Die Zinsen werden jährlich dem Sparbetrag gutgeschrieben.
Überprüfe, ob die Reise von gespartem Geld bezahlt werden kann, wenn man
(1 Pkt.)
7.
Die Parabel 
(siehe Abbildung) wird an der 
-Achse gespiegelt.
Welche Funktionsgleichung hat die neue Parabel?
Kreuze an.
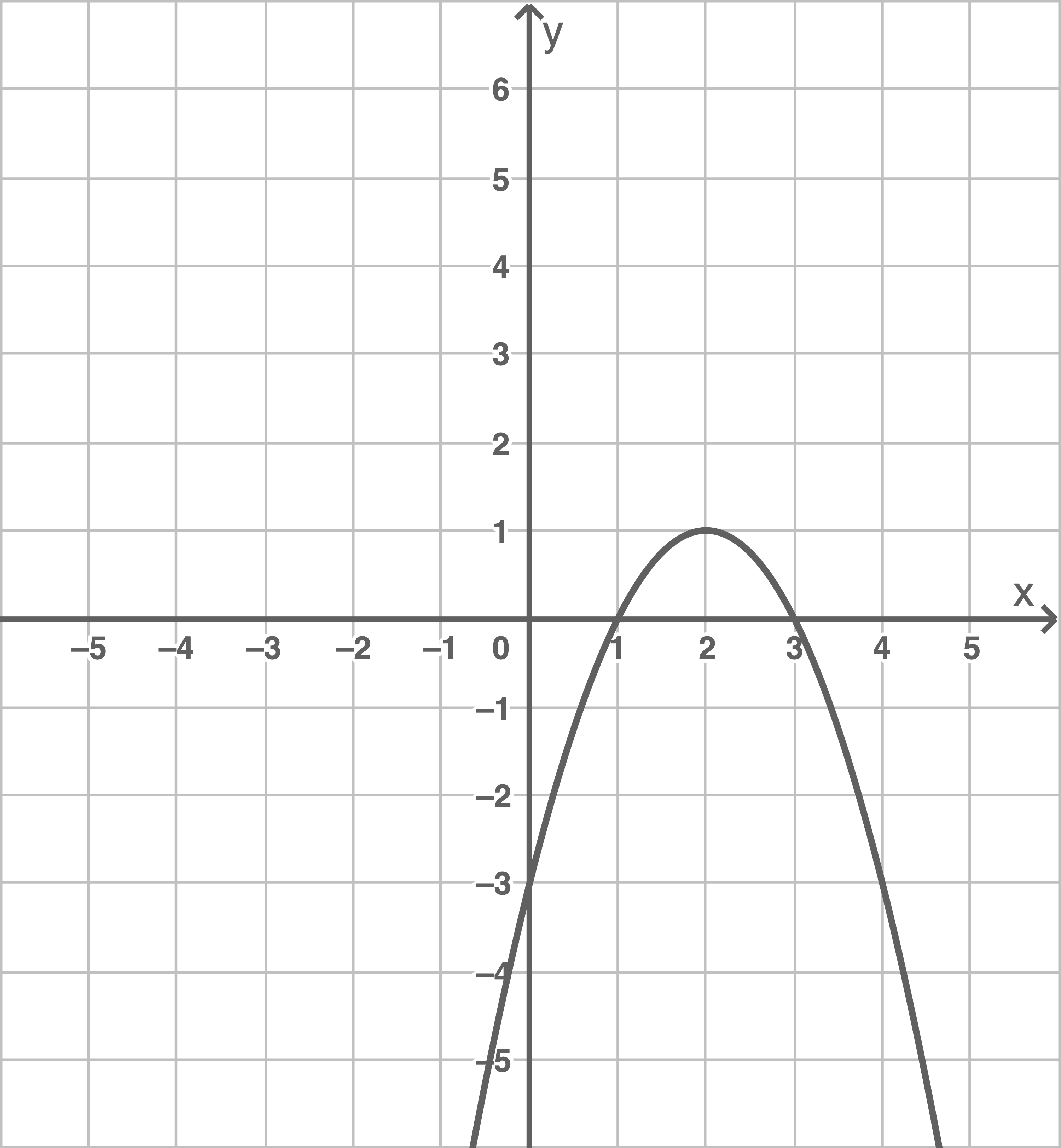
Kreuze an.
(1 Pkt.)
8.
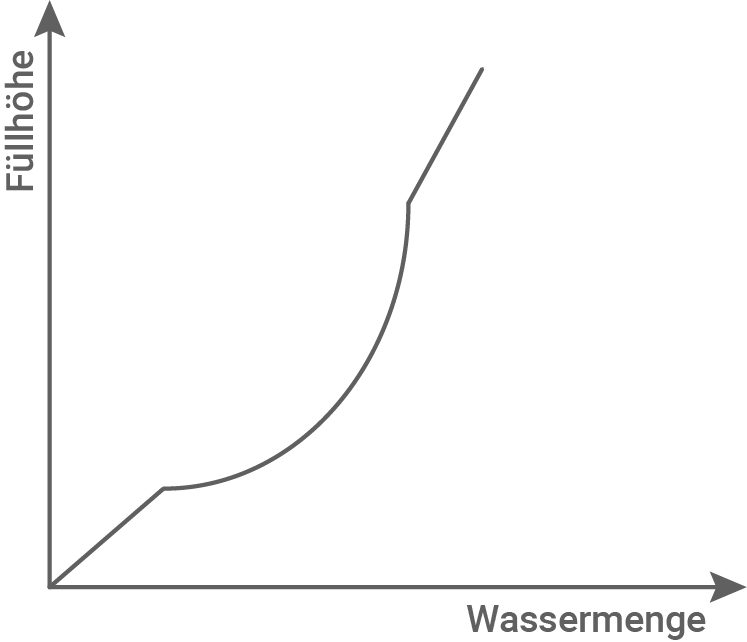
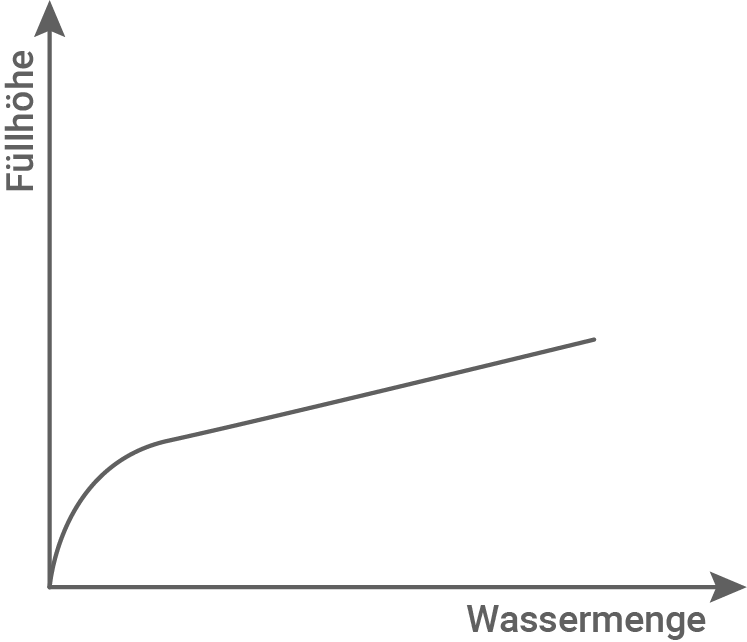
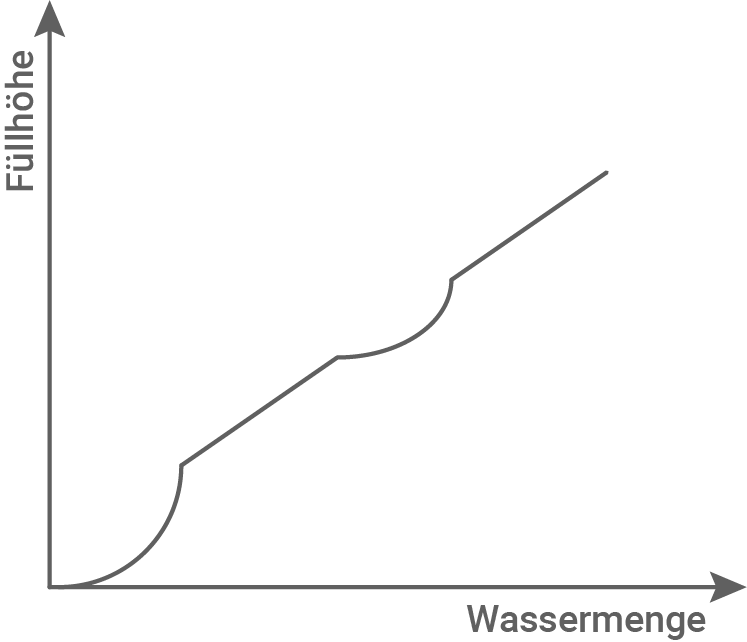
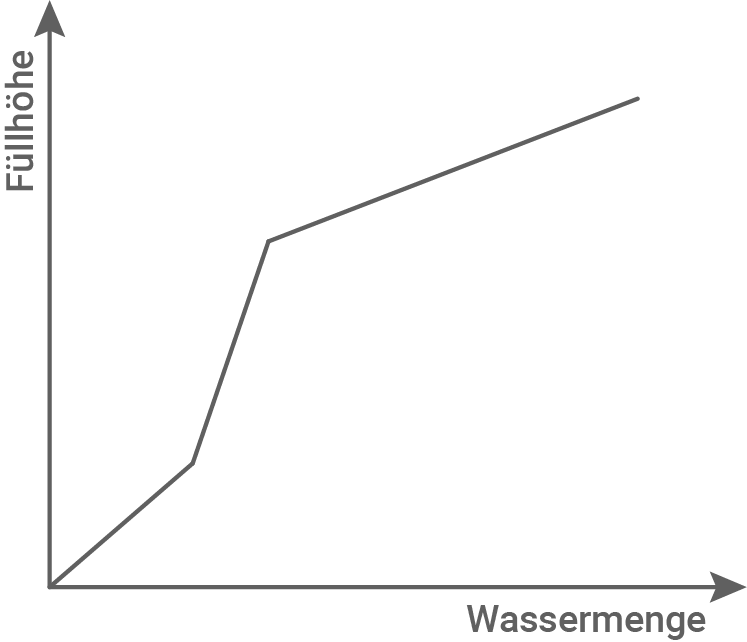
Die abgebildete Blumenvase wird befüllt.
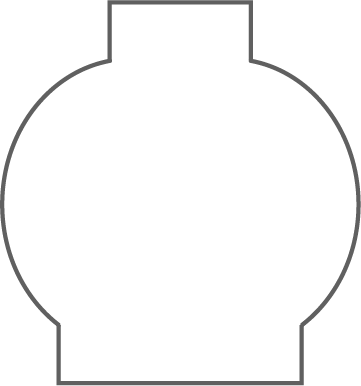Kreuze das richtige Fülldiagramm an.
Diagramm A
|
Diagramm B
|
Diagramm C
|
Diagramm D
|
(1 Pkt.)
9.
Lotta und ihre Freundinnen unterhalten sich über ihre Urlaubsziele.
Diese sind von Stuttgart aus durchschnittlich
entfernt.
Wo war Lotta im Urlaub?
Begründe die Auswahl deines Ergebnisses rechnerisch.
Diese sind von Stuttgart aus durchschnittlich
| Maria | Athen | |
| Betty | Rom | |
| Claudia | Kairo | |
| Sevtap | Antalya | |
| Lotta | ? | |
| Svenja | Hamburg | |
| Yvonne | Gardasee | |
| Riccarda | Berlin | |
Begründe die Auswahl deines Ergebnisses rechnerisch.
| Paris |
|
| Mallorca |
|
| Wien |
| Dublin |
|
| Amsterdam |
|
| Monaco |
(1 Pkt.)
10.
In einem Beutel befinden sich 
gelbe, rote, 
blaues und grüne Plättchen.
Es wird zweimal ohne Zurücklegen gezogen. Wie hoch ist die Wahrscheinlichkeit, ein gelbes und ein rotes Plättchen zu ziehen?
Die Reihenfolge spielt keine Rolle.
Es wird zweimal ohne Zurücklegen gezogen. Wie hoch ist die Wahrscheinlichkeit, ein gelbes und ein rotes Plättchen zu ziehen?
Die Reihenfolge spielt keine Rolle.
(1 Pkt.)
1.
2.
Lösung über das Einsetzungsverfahren
Gleichung 
nach 
auflösen
![\(\begin{array}[t]{rll}
\text{(I)}\quad&36&=& x + y&\quad \scriptsize \mid\;-x \\[5pt]
\text{(I](https://mathjax.schullv.de/1f49a64ddaae694a6300a791d946b633b298213b8fa020c66c1d66bb392b6c45?color=5a5a5a)
Gleichung 
in Gleichung 
einsetzen
![\(\begin{array}[t]{rll}
4x+2y&=&114 & \\[5pt]
4x+2\cdot (36-x)&=&114 & \\[5pt]
4x+72-2x&=&114 \\[5pt]
2x+72&=&114 &\quad \scriptsize \mid\;-72 \\[5pt]
2x&=&42 &\quad \scriptsize \mid\;:2 \\[5pt]
\boldsymbol{x}&=&\boldsymbol{21}
\end{array}\)](https://mathjax.schullv.de/58c8b8d79748063258aaf8eb2293411b671655e61b35edeaf2c2a08b914ae997?color=5a5a5a)
in Gleichung einsetzen
![\(\begin{array}[t]{rll}
y&=&36-x&\\[5pt]
y&=&36-21&\\[5pt]
\boldsymbol{y}&=&\boldsymbol{15}
\end{array}\)](https://mathjax.schullv.de/bd4214d1925f18a5a2d2c90e428dde37d1cb016267871e359d9bfcb99c7726cc?color=5a5a5a)
3.
Den 2. Strahlensatz anwenden:
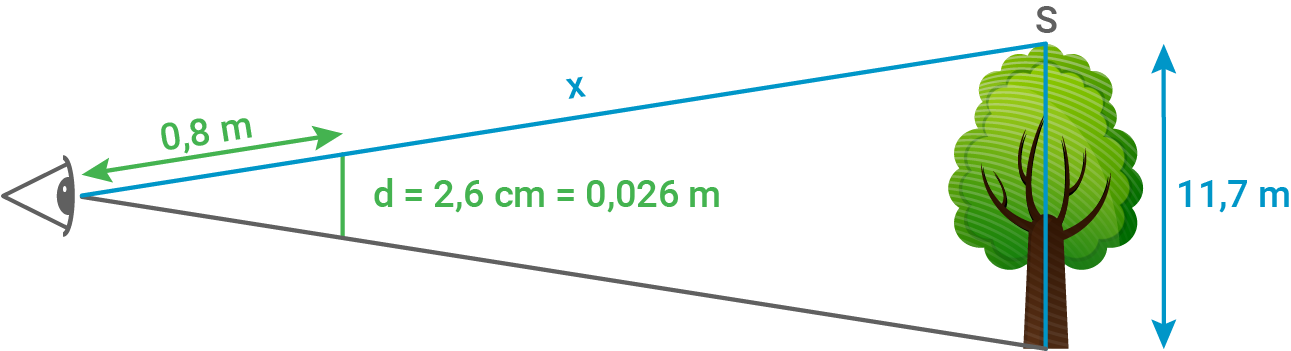
![\(\begin{array}[t]{rll}
\dfrac{11,7\,\text{m}}{x}&=& \dfrac{d}{0,8\,\text{m}}&\scriptsize \mid\;\cdot x \\[5pt]
11,7\,\text{m}&=& \dfrac{d}{0,8\,\text{m}}\cdot x&\scriptsize \mid\;\cdot \dfrac{0,8\,\text{m}}{d}\\[5pt]
11,7\,\text{m}\cdot \dfrac{0,8\,\text{m}}{d}&=& x&\\[5pt]
x&=&11,7\,\text{m}\cdot \dfrac{0,8\,\text{m}}{0,026\,\text{m}}&\\[5pt]
x&=&\boldsymbol{360\,\text{m}}&\\[5pt]
\end{array}\)](https://mathjax.schullv.de/27e189a356cbdd9f6a695b5a4243798c74734e0f700b899b379bff4339f151e8?color=5a5a5a)
4.
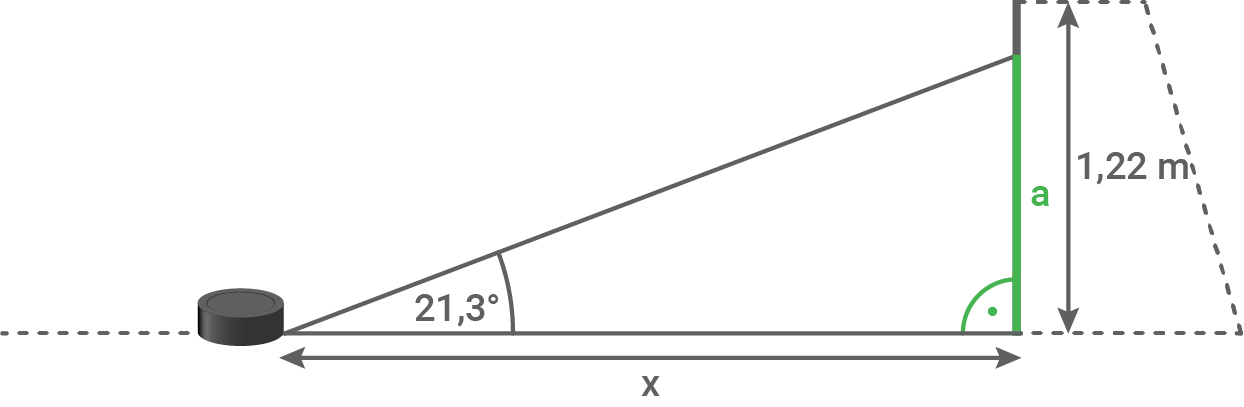
5.
Innenradius berechnen
Hilfsskizze
Der Radius des Zylinders entspricht dem Radius der Kugel.
Um den Radius zu berechnen, wird die Formel zur Berechnung des Volumens einer Kugel nach 
umgestellt:
![\(\begin{array}[t]{rll}
V&=&\dfrac{4}{3}\cdot \pi\cdot r^3 &\quad \scriptsize \mid\;\cdot \dfrac{3}{4} \\[5pt]
\dfrac{3}{4}\cdot V&=&\pi\cdot r^3 &\quad \scriptsize \mid\;:\pi\\[5pt]
\dfrac{3}{4}\cdot \dfrac{V}{\pi}&=&r^3 &\\[5pt]
r^3&=&\dfrac{3}{4}\cdot \dfrac{V}{\pi} &\quad \scriptsize \mid\;\sqrt[3]{\,\,}\\[5pt]
r&=& \sqrt[3]{\dfrac{3}{4}\cdot \dfrac{V}{\pi}} &\\[5pt]
r&=& \sqrt[3]{\dfrac{3}{4}\cdot \dfrac{524\,\text{cm}^3}{\pi}} &\\[5pt]
r&\approx& \boldsymbol{5\,\text{cm}}
\end{array}\)](https://mathjax.schullv.de/4e1189d2dcccb24b610174ba79cb835f41dd6d6538209ed266ca62cfff3241db?color=5a5a5a)
Innenhöhe des Zylinders berechnen
Die Höhe des Zylinders entspricht dem Durchmesser der Kugel.
6.
Gegeben:
![\(\begin{array}[t]{rll}
K_n&=&K_0\cdot \left(1+\dfrac{p}{100}\right)^n \\[5pt]
K_6&=&1\,990\,€\cdot \left(1+\dfrac{1,8}{100}\right)^6 \\[5pt]
K_6&=&1\,990\,€\cdot 1,18^6 \\[5pt]
K_6&\approx&2\,214,83\,€ \\[5pt]
\end{array}\)](https://mathjax.schullv.de/28c815efd3c0e2667033d7bc3416f4e6789917bb1f2028a099666663e8f4842d?color=5a5a5a)
Die Reise kann mit dem gesparten Geld bezahlt werden.
Jahre
7.
8.
Diagramm A
9.
Lotta und ihre Freundinnen sind insgesamt 
weit gereist.
Also beträgt Lottas Reisestrecke:
Lotta war in Wien im Urlaub.
10.
Wahrscheinlichkeiten beim 1. Zug:
![\(\begin{array}[t]{rll}
P(\text{gelb und rot})&=& P(\text{gelb; rot})+P(\text{rot; gelb}) \\[5pt]
&=& \dfrac{3}{8}\cdot \dfrac{2}{7}+\dfrac{2}{8}\cdot \dfrac{2}{7} \\[5pt]
&=& \boldsymbol{\dfrac{3}{14}} \\[5pt]
&\approx& \boldsymbol{21,4\,\%}
\end{array}\)](https://mathjax.schullv.de/cf35c25d7dee9cb1cd8567f3ebc837d925a8acaa9b464b6b496738eb5c4e7570?color=5a5a5a)