Pflichtaufgaben
1
Im Jahr 2015 verbrauchte Deutschlands Bevölkerung pro Kopf  Süßwaren.
Süßwaren.
 gesunken.
gesunken.
 jährlich.
jährlich.
| Arten von Süßwaren | Pro-Kopf-Verbrauch |
|---|---|
| Schokoladenwaren | |
| kakaohaltige Lebensmittel | |
| Zuckerwaren | |
| feine Backwaren | |
| Knabbergebäck | |
| Speiseeis |
Nach Bundesverband der Deutschen Süßwarenindustrie e.V.
a)
Stelle den Anteil von Schokoladenwaren an den insgesamt verbrauchten Süßwaren in einem Kreisdiagramm dar.
Vom Jahr 2014 zum Jahr 2015 ist der Pro-Kopf-Verbrauch von Speiseeis um
2 BE
b)
Berechne den Pro-Kopf-Verbrauch von Speiseeis für das Jahr 2014.
Die Süßwarenindustrie erwartet bis zum Jahr 2020 einen weiteren Anstieg des Verbrauchs von Knabbergebäck um
2 BE
c)
Berechne den Pro-Kopf-Verbrauch von Knabbergebäck, den die Süßwarenindustrie für das Jahr 2020 erwartet.
1 BE
2
Die Wertetabelle enthält Zahlenpaare der Funktion  mit
mit 
a)
Stelle die Funktion  grafisch dar und gib die Funktionsgleichung an.
grafisch dar und gib die Funktionsgleichung an.
2 BE
b)
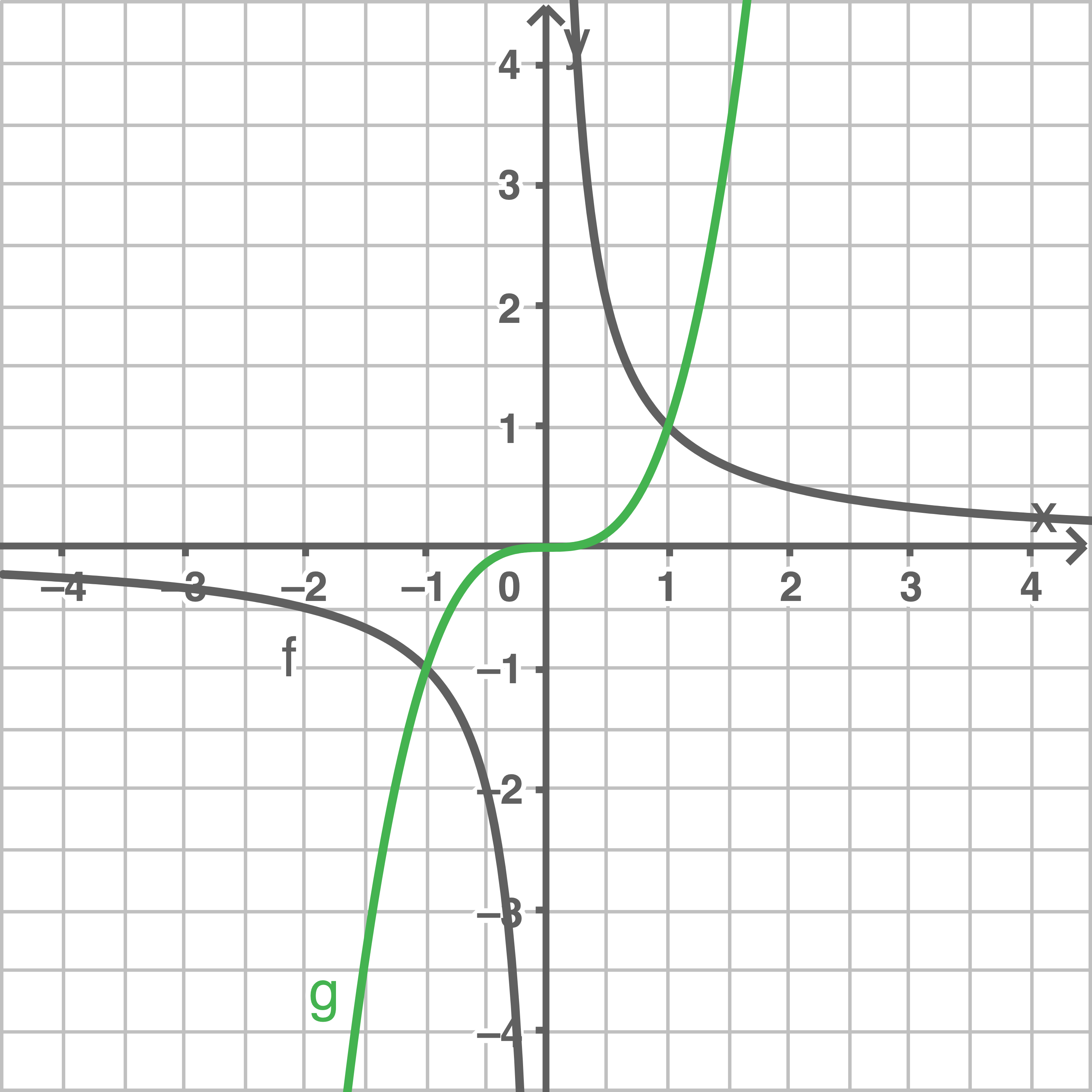
Skizziere den Graphen der Funktion  mit
mit  für mindestens
für mindestens  in dasselbe Koordinatensystem.
in dasselbe Koordinatensystem.
1 BE
c)
Gib eine gemeinsame Eigenschaft der Funktionen  und
und  an.
an.
1 BE
3
Die wahrscheinlich steilste Straße Deutschlands befindet sich in Deesbach im Landkreis Saalfeld-Rudolstadt. Die  lange Straße hat eine Steigung von
lange Straße hat eine Steigung von 
Berechne den Anstiegswinkel der Straße.
Berechne den Anstiegswinkel der Straße.
1 BE
4
Im Handel werden Sonnenschutzsegel in verschiedenen Formen angeboten.
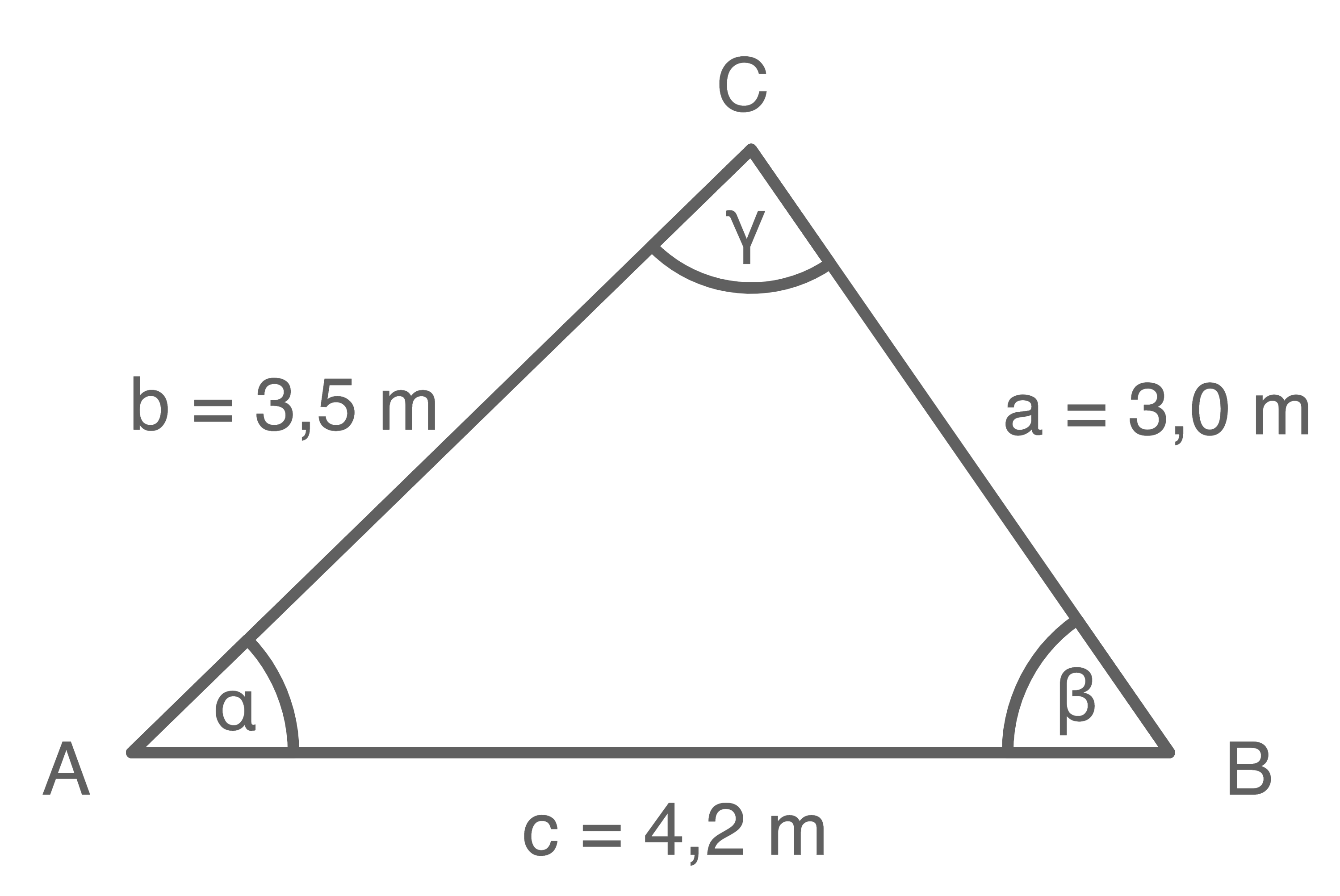
Ein Sonnenschutzsegel hat die Form eines Dreiecks mit den Seitenlängen
 und
und  Für das verwendete Material werden
Für das verwendete Material werden  je Quadratmeter angegeben.
Berechne die Masse dieses Sonnensegels.
je Quadratmeter angegeben.
Berechne die Masse dieses Sonnensegels.
Ein Sonnenschutzsegel hat die Form eines Dreiecks mit den Seitenlängen
3 BE
5
In einer Urne befinden sich 5 weiße und 5 schwarze Kugeln, die jeweils von 1 bis 5 nummeriert sind.
 ein.
ein.
a)
Berechne die Wahrscheinlichkeit dafür, dass beim einmaligen Ziehen eine Kugel mit der Zahl 4 entnommen wird.
Beim einmaligen Ziehen einer Kugel tritt ein anderes Ereignis mit einer Wahrscheinlichkeit von
1 BE
b)
Formuliere ein solches Ereignis in Worten.
1 BE
c)
Berechne die Wahrscheinlichkeit für das Ereignis:
„Beim zweimaligen Ziehen ohne Zurücklegen erhält man zwei schwarze Kugeln.“
1 BE
6
Im Wetterbericht wird eine Regenmenge von 20 Liter pro Quadratmeter angegeben. Diese Regenmenge wird in einem quaderförmigen Behälter mit einer Grundfläche von einem Quadratmeter aufgefangen.
Berechne die Höhe des Wasserstandes in diesem Behälter.
2 BE
7
Bei einem umlaufenden Sessellift befindet sich die Talstation in  Höhe und die Bergstation in
Höhe und die Bergstation in  Höhe. Je Minute überwinden die Sessel einen Höhenunterschied von
Höhe. Je Minute überwinden die Sessel einen Höhenunterschied von  Zwei Wanderer besteigen gleichzeitig den Lift, einer an der Berg- und der andere an der Talstation.
Zwei Wanderer besteigen gleichzeitig den Lift, einer an der Berg- und der andere an der Talstation.
 beschrieben werden.
beschrieben werden.
a)
Bestimme die Höhe, in der beide aneinander vorbeifahren.
Der Höhenunterschied der Talfahrt kann durch
1 BE
b)
Gib für die Bergfahrt die Gleichung an, die diese Fahrt beschreibt.
1 BE
8
Gegeben sind die folgenden Körper (Zylinder, Halbkugel und Kegel) mit jeweils demselben Radius. Für alle Körper gilt 
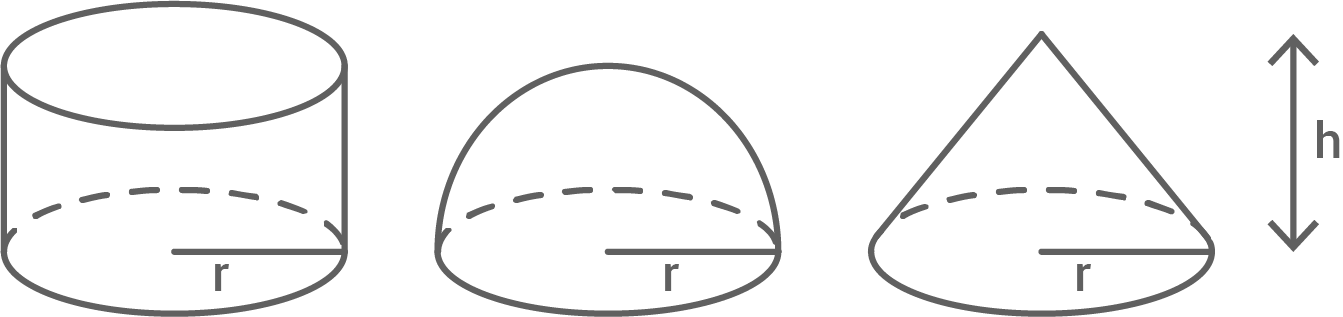

Skizzen nicht maßstäblich
a)
Stelle einen der Körper mit geeigneten Maßen im Zweitafelbild dar.
2 BE
b)
Berechne das Volumen des Kegels, wenn der Zylinder ein Volumen von  hat.
hat.
Marie behauptet: „Addiert man das Volumen der Halbkugel und das Volumen des Kegels, so erhält man das Volumen des Zylinders.“
1 BE
c)
Zeige an einem selbst gewählten Beispiel oder durch logische Schlussfolgerung, dass Maries Behauptung richtig ist.
1 BE
1
a)
Zuerst wird der prozentuale Anteil der Schokoladenwaren an den gesamten Süßwaren berechnet:
Lösung mit der Lösungsformel


![\(\begin{array}[t]{rll}
p\,\%&=& \dfrac{W}{G}\cdot 100\,\% \\[5pt]
p\,\%&=& \dfrac{9,79\,\text{kg}}{32,40\,\text{kg}}\cdot 100\,\% \\[5pt]
p\,\%&\approx& 30,2\,\%
\end{array}\)](https://www.schullv.de/resources/formulas/e1e736f56aadcf7078ff9d65fcdf2b9614c40697f5412f393f40b228c010c1bf_light.svg) Lösung mit Dreisatz
Lösung mit Dreisatz




![\(\begin{array}{rcl}
32,40\,\text{kg}& \mathrel{\widehat{=}}& 100\,\%\\[5pt]
1\,\text{kg} & \mathrel{\widehat{=}}& \dfrac{100}{32,40}\,\%\\[5pt]
9,79 \,\text{kg} & \mathrel{\widehat{\approx}}& 30,2\,\%\,€
\end{array}\)](https://www.schullv.de/resources/formulas/df8ad66afb7653b8530c4b3ae5adfe9ab966beab92a64c47d08437dca27eabd5_light.svg)



 Für die Größe des Mittelpunktswinkels des zugehörigen Kreissektors folgt daher:
Für die Größe des Mittelpunktswinkels des zugehörigen Kreissektors folgt daher:



Pro-Kopf-Verbrauch der gesamten Süßwaren
b)
Lösung mit der Lösungsformel


![\(\begin{array}[t]{rll}
G&=& \dfrac{W\cdot 100\,\%}{p\,\%} \\[5pt]
G&=& \dfrac{3,63\,\text{kg}\cdot 100\,\%}{88,3\,\%} \\[5pt]
G&\approx& 4,11\,\text{kg}
\end{array}\)](https://www.schullv.de/resources/formulas/5878b36db5fe11d79091733f38429ffdd083af184aba69bce157d5e7e74d4c29_light.svg) Lösung mit Dreisatz
Lösung mit Dreisatz




![\(\begin{array}{rrcll}
& 88,3\,\% &\mathrel{\widehat{=}}& 3,63\,\text{kg}\\[5pt]
& 1\,\% &\mathrel{\widehat{=}}& \dfrac{3,63}{88,3}\,\text{kg}\\[5pt]
& 100\,\%&\mathrel{\widehat{=}}& 4,11\,\text{kg}&
\end{array}\)](https://www.schullv.de/resources/formulas/d13bcbc35564a5fa03dc8c9a77af032ee51b7dd2e73d8b71880c487460a6c4f5_light.svg)



 Im Jahr 2014 wurden pro Kopf also ca.
Im Jahr 2014 wurden pro Kopf also ca.  Speiseeis verbraucht.
Speiseeis verbraucht.
c)
2
a)
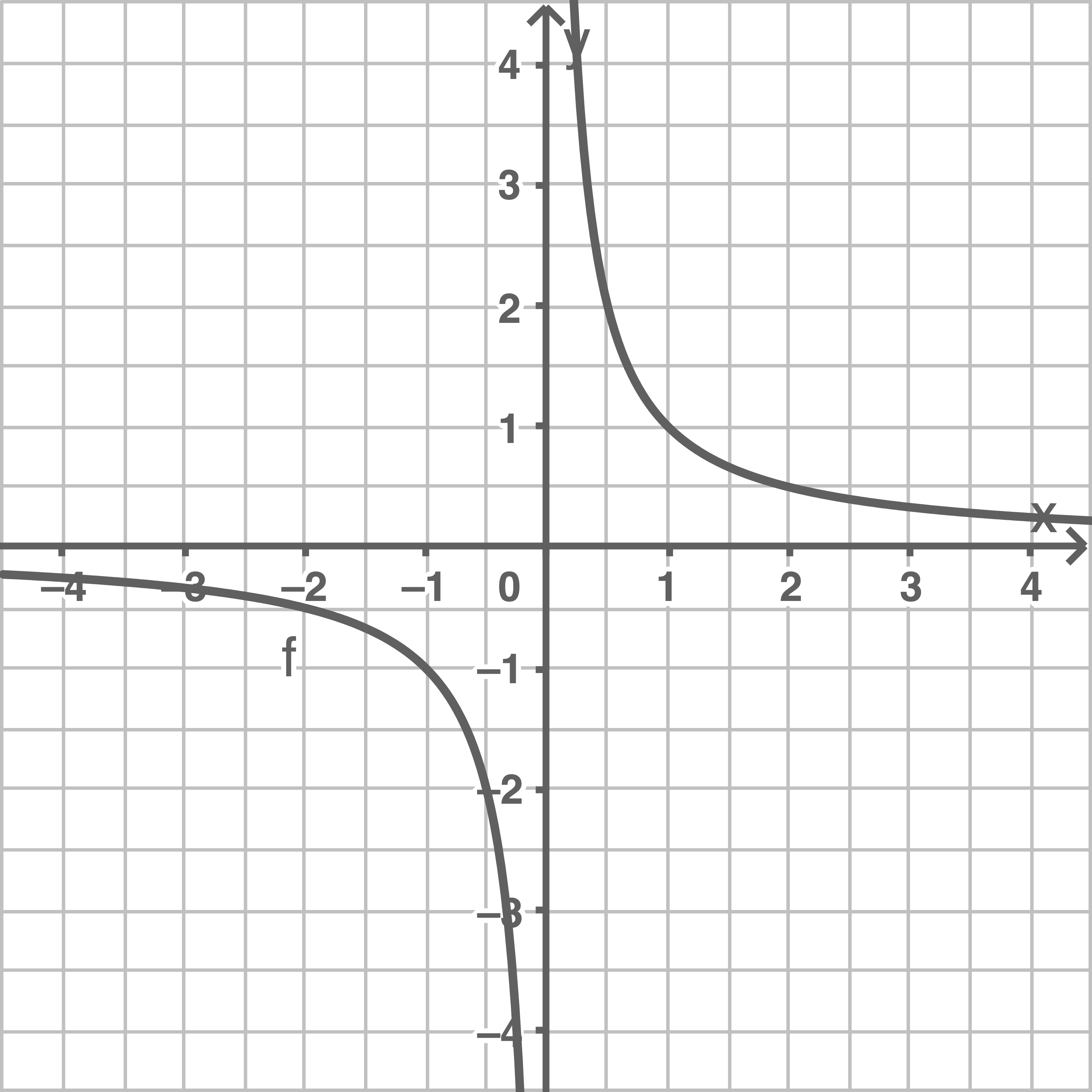
b)
Wertetabelle für  erstellen:
erstellen:
| -1,5 | -3,375 |
| -1 | -1 |
| -0,5 | -0,125 |
| 0 | 0 |
| 0,5 | 0,125 |
| 1 | 1 |
| 1,5 | 3,375 |

c)
Mögliche gemeinsame Eigenschaften:
- Beide Graphen verlaufen durch die Punkte
und
- Beide Graphen sind punktsymmetrisch zum Koordinatenursprung.
- Die Graphen beider Funktionen verlaufen im I. und III. Quadranten.
3
Ein Anstieg von  bedeutet pro
bedeutet pro  horizontaler Entfernung einen Höhenunterschied von
horizontaler Entfernung einen Höhenunterschied von  Skizze des Sachverhalts:
Skizze des Sachverhalts:
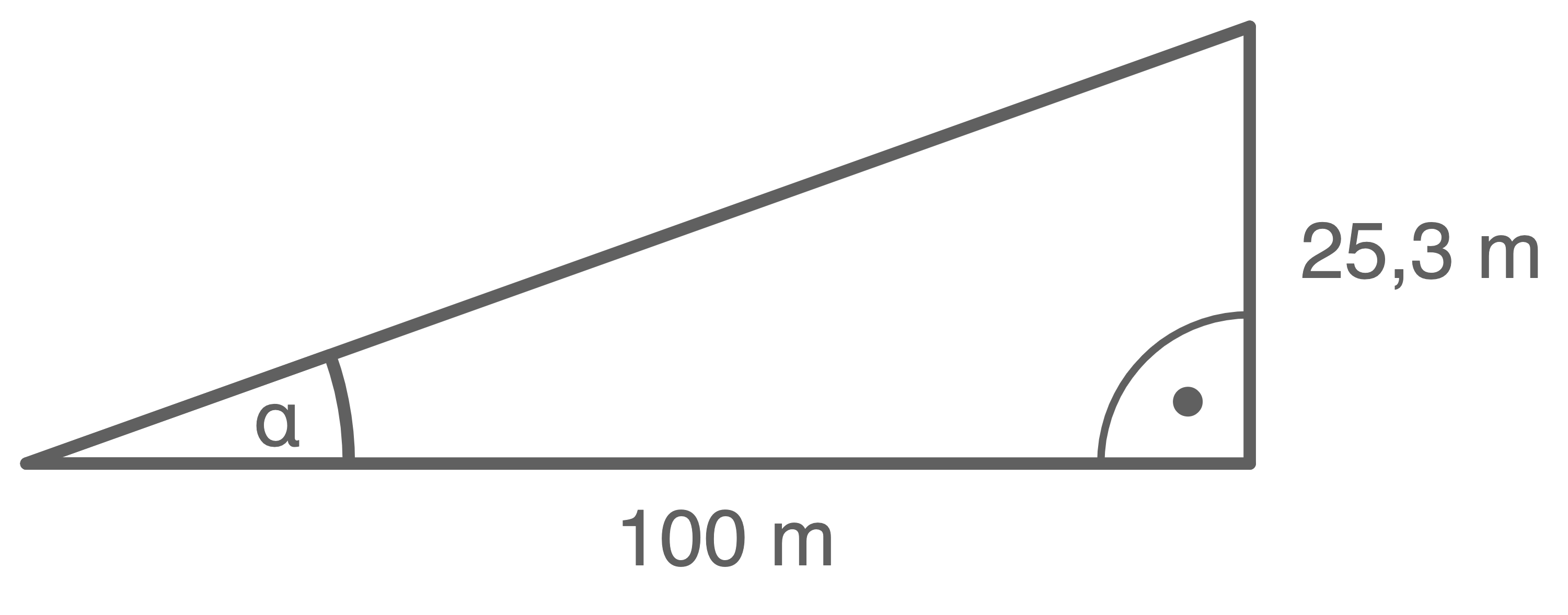 Der Winkel
Der Winkel  kann mit dem Tangens berechnet werden.
kann mit dem Tangens berechnet werden.
![\(\begin{array}[t]{rll}
\tan \alpha &=& \dfrac{\text{Gegenkathete}}{\text{Ankathete}} \\[5pt]
\tan \alpha &=& \dfrac{25,3\,\text{m}}{100\,\text{m}} \quad \scriptsize \mid\; \tan^{-1}\\[5pt]
\alpha&\approx& 14,2^{\circ}
\end{array}\)](https://www.schullv.de/resources/formulas/008a3586a863afee5fb6ca1204f4334f2783f6b6027df2e5551bf8610331a356_light.svg) Der Anstiegswinkel der Straße ist ungefähr
Der Anstiegswinkel der Straße ist ungefähr  groß.
groß.

4
5
a)
10 mögliche Ergebnisse: 5 weiße und 5 schwarze Kugeln
2 günstige Ergebnisse: 1 weiße und 1 schwarze Kugel mit Zahl 4![\(\begin{array}[t]{rll}
& P(\text{Kugel mit 4}) \\[5pt]
=& \dfrac{\text{Anzahl günstige Ergebnisse}}{\text{Anzahl mögliche Ergebnisse}} \\[5pt]
=& \dfrac{2}{10} \\[5pt]
=& \dfrac{1}{5}
\end{array}\)](https://www.schullv.de/resources/formulas/8bfc794f362be50bd7908bfba3e29b4415d9d578d829380c6cb7cb73b8e4c888_light.svg) Die Wahrscheinlichkeit für das Ziehen einer Kugel mit der Zahl 4 beträgt
Die Wahrscheinlichkeit für das Ziehen einer Kugel mit der Zahl 4 beträgt 
2 günstige Ergebnisse: 1 weiße und 1 schwarze Kugel mit Zahl 4
b)
Gesucht ist ein Ereignis, für dessen Eintreten 6 Kugeln infrage kommen. Es gibt beispielsweise 6 Kugeln mit ungeraden Zahlen. Ein mögliches Ereignis wäre also beispielsweise:
„Beim einmaligen Ziehen wird eine Kugel mit einer ungerade Zahl gezogen.“
c)
Es handelt sich um ein zweistufiges Zufallsexperiment mit Ziehen ohne Zurücklegen. Mit der Pfadmultiplikationsregel folgt:
 Mit einer Wahrscheinlichkeit von
Mit einer Wahrscheinlichkeit von  werden beim zweimaligen Ziehen ohne Zurücklegen zwei schwarze Kugeln gezogen.
werden beim zweimaligen Ziehen ohne Zurücklegen zwei schwarze Kugeln gezogen.
6
In dem Behälter mit der Grundfläche von einem Quadratmeter befinden sich 20 Liter Wasser:
 Mit der Formel für das Volumen eines Quaders ergibt sich:
Mit der Formel für das Volumen eines Quaders ergibt sich:
![\(\begin{array}[t]{rll}
V &=& G\cdot h \\[5pt]
0,02\,\text{m}^3 &=& 1\,\text{m}^2 \cdot h&\quad \scriptsize \mid\; : 1\,\text{m}^2\\[5pt]
0,02\,\text{m}&=& h
\end{array}\)](https://www.schullv.de/resources/formulas/b867b470be64c9ed6e6e01f434b3333b1d40d978b6e59749d2f68fdfff15d2af_light.svg) Die Höhe des Wasserstandes in dem Behälter beträgt
Die Höhe des Wasserstandes in dem Behälter beträgt 
7
a)
Da beide mit der gleichen Geschwindigkeit unterwegs sind, treffen sich die Wanderer in der Mitte:
 Die Wanderer fahren also in einer Höhe von
Die Wanderer fahren also in einer Höhe von  aneinander vorbei.
aneinander vorbei.
b)
Gesucht ist die Gleichung der Form  die die Bergfahrt beschreibt.
Im Gegensatz zur Talfahrt muss die Steigung bei der Bergfahrt positiv sein. Der Sessellift fährt aber genauso schnell den gleichen Anstieg hoch, wie er herunter fährt. Daher ist die Steigung
die die Bergfahrt beschreibt.
Im Gegensatz zur Talfahrt muss die Steigung bei der Bergfahrt positiv sein. Der Sessellift fährt aber genauso schnell den gleichen Anstieg hoch, wie er herunter fährt. Daher ist die Steigung  Der
Der  -Achsenabschnitt muss die Starthöhe sein, also
-Achsenabschnitt muss die Starthöhe sein, also  Die Gleichung, die die Bergfahrt beschreibt, lautet:
Die Gleichung, die die Bergfahrt beschreibt, lautet:

8
a)
Im Folgenden sind alle drei Zweitafelbilder aufgeführt. Es ist jedoch nur eines gefordert.
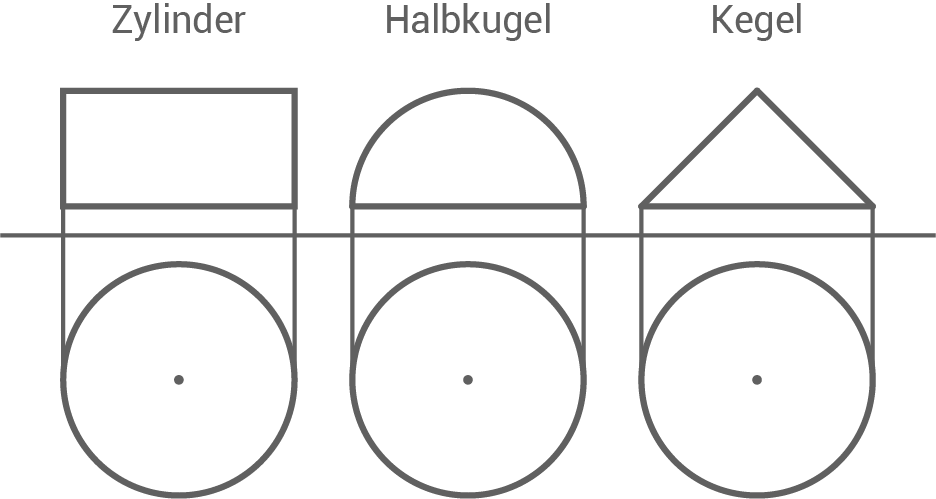
b)
Mit der Formel für das Volumen eines Zylinders lässt sich der Radius  berechnen:
berechnen:
![\(\begin{array}[t]{rll}
V&=& \pi \cdot r^2 \cdot h \quad \scriptsize \mid\;h=r\\[5pt]
450\,\text{cm}^3&=& \pi\cdot r^2\cdot r \quad \scriptsize \mid\;:\pi \\[5pt]
\dfrac{450}{\pi}\,\text{cm}^3&=& r^3 \quad \scriptsize \mid\;\sqrt[3]{\,} \\[5pt]
\sqrt[3]{\dfrac{450}{\pi}}\,\text{cm}&=& r \\[5pt]
5,23 \,\text{cm}&\approx& r
\end{array}\)](https://www.schullv.de/resources/formulas/7c44a10d5629109c3cf9bfa6d32dc451a76bb426604b17e2e91ee641f0cf505b_light.svg) Da der Zylinder und der Kegel den gleichen Radius haben, folgt mit der Formel für das Volumen eines Kegels:
Da der Zylinder und der Kegel den gleichen Radius haben, folgt mit der Formel für das Volumen eines Kegels:
![\(\begin{array}[t]{rll}
V_{\text{Kegel}}&=& \dfrac{1}{3}\cdot \pi \cdot r^2 \cdot h \quad \scriptsize \mid\; h=r \\[5pt]
&=& \dfrac{1}{3}\cdot \pi \cdot r^3 \quad \scriptsize \mid\;r=5,23\,\text{cm} \\[5pt]
&=& \dfrac{1}{3}\cdot \pi \cdot (5,23 \,\text{cm})^3\\[5pt]
&\approx& 150\,\text{cm}^3
\end{array}\)](https://www.schullv.de/resources/formulas/95e424931127b34f4630517eac81967808537319940ca36a4de25a552d7ab237_light.svg) Wenn das Volumen des Zylinders
Wenn das Volumen des Zylinders  beträgt, dann beträgt das Volumen des Kegels
beträgt, dann beträgt das Volumen des Kegels 
c)
Mit den entsprechenden Volumenformeln gilt für 
![\(\begin{array}[t]{rll}
V_{\text{Zylinder}}&= \pi\cdot r^3 \\[10pt]
V_{\text{Halbkugel}}&= \dfrac{1}{2}\cdot\dfrac{4}{3}\cdot \pi \cdot r^3 \\[5pt]
&= \dfrac{2}{3}\cdot \pi \cdot r^3 \\[10pt]
V_{\text{Kegel}}&= \dfrac{1}{3}\cdot \pi \cdot r^3
\end{array}\)](https://www.schullv.de/resources/formulas/de20afbd2aaac1775ccc01354c7ee3434b2c09dc9d971d9bae510ac5608425f2_light.svg) Es gilt also:
Es gilt also:
![\(\begin{array}[t]{rll}
& V_{\text{Halbkugel}} + V_{\text{Kegel}}\\[5pt]
=& \dfrac{2}{3}\cdot \pi \cdot r^3 + \dfrac{1}{3}\cdot \pi \cdot r^3 \\[5pt]
=& \pi \cdot r^3 \\[5pt]
=& V_{\text{Zylinder}}
\end{array}\)](https://www.schullv.de/resources/formulas/4aeb2543a0bebe846dc28135b0b5e66af70ea8485a0304e8339692fc3b7c12e3_light.svg) Marie hat also recht.
Marie hat also recht.