Pflichtaufgaben
1
Biokunststoffe sind aus nachwachsenden Rohstoffen hergestellte Kunststoffe.
In der Tabelle ist die weltweite Produktion von Biokunststoffen angegeben.
Nach: Biobasierte Wirtschaft als Wachstumstreiber. In: Neue Produkte: Aus Natur gemacht. Bundesministerium für Ernährung, Landwirtschaft und Verbraucherschutz, S. 23.
In der Tabelle ist die weltweite Produktion von Biokunststoffen angegeben.
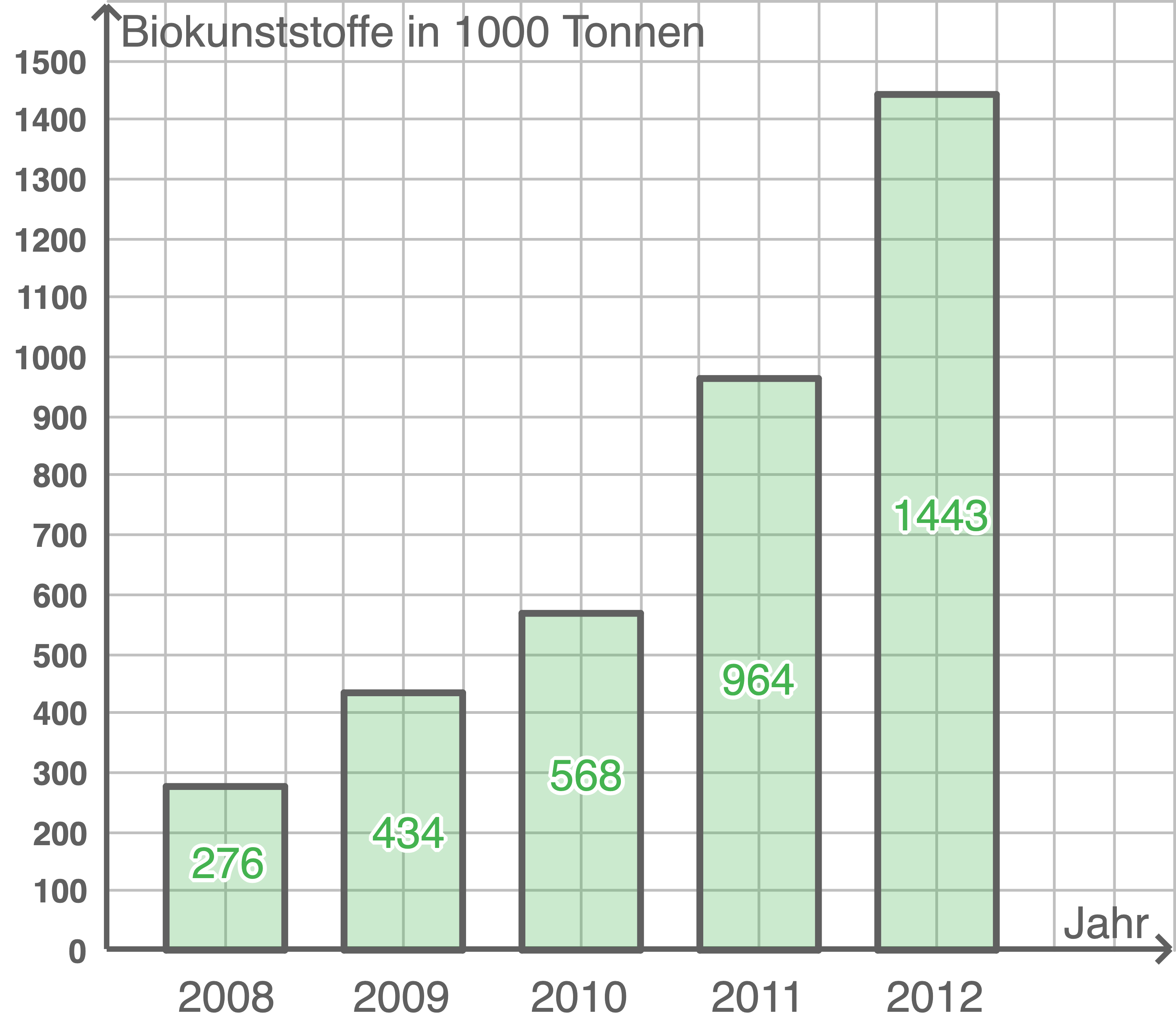
| Jahr | Biokunststoffe in 1000 Tonnen |
|---|---|
| 2008 |
276
|
| 2009 |
434
|
| 2010 |
568
|
| 2011 |
964
|
| 2012 |
1 443
|
a)
Stelle diesen Sachverhalt in einem geeigneten Diagramm dar.
2 BE
b)
Auf wie viel Prozent hat sich die weltweite Produktion von Biokunststoffen im Jahr 2012 gegenüber dem Jahr 2011 erhöht?
Für das Jahr 2016 wird angenommen, dass sich die weltweite Produktion von Biokunststoffen gegenüber 2012 etwa vervierfacht.
1 BE
c)
Zeige, dass man bei dieser Annahme von einer jährlichen Zunahme von  ausgeht.
ausgeht.
1 BE
2
Gegeben sind die Dreiecke  und
und 
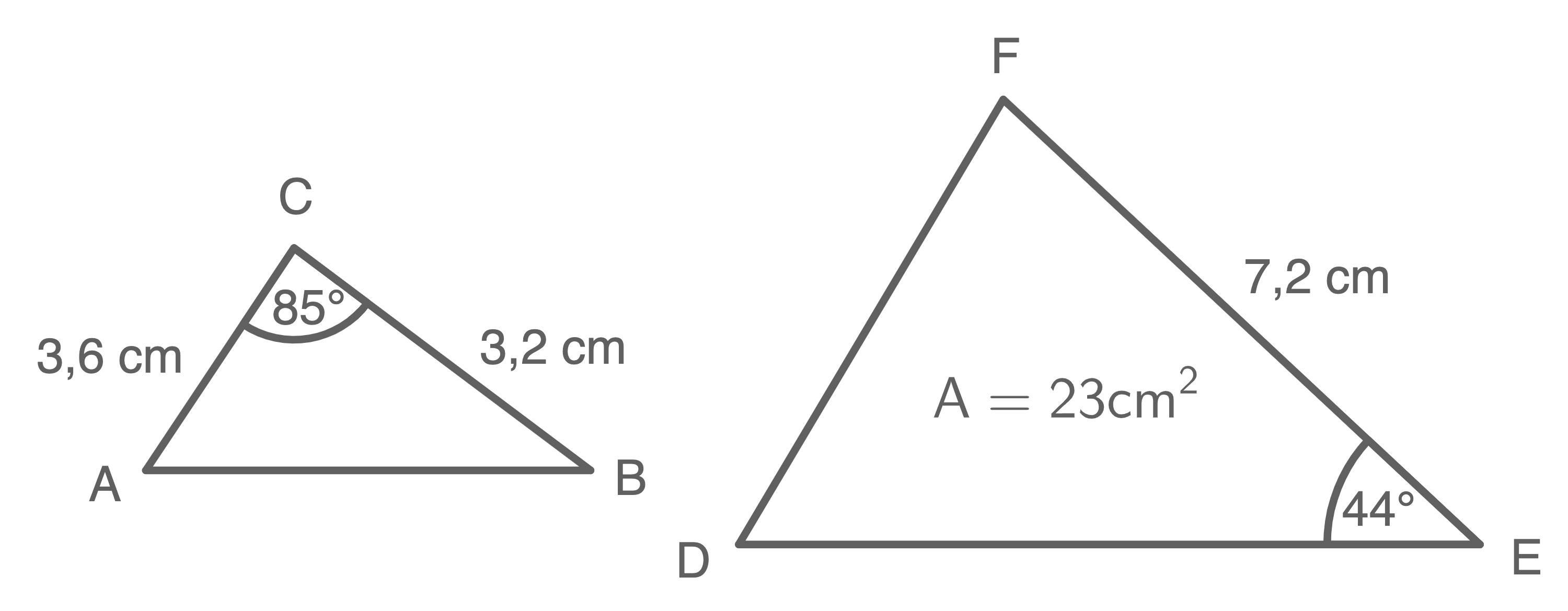 Zeige rechnerisch, dass etwa
Zeige rechnerisch, dass etwa  gilt.
gilt.

Skizzen nicht maßstäblich
3 BE
3
Löse das Gleichungssystem.
![\(\begin{array}[t]{lllllll}
\text{I}&y&+&3&=& x \\[5pt]
\text{II}&2y&+&4x&=& 6
\end{array}\)](https://www.schullv.de/resources/formulas/5c7283d078ec52d198267cf6eb13a3e6089200e34381c87d8d00fb4d5bec2676_light.svg)
3 BE
4
Gegeben sind die Funktionen  und
und  mit
mit 
 und
und  ist
ist  Der Scheitelpunkt von
Der Scheitelpunkt von  ist
ist 
a)
Berechne die Nullstellen von 
1 BE
b)
Stelle  und
und  in ein und demselben Koordinatensystem
in ein und demselben Koordinatensystem  graphisch dar.
graphisch dar.
Der Schnittpunkt von
2 BE
c)
Berechne die Länge der Strecke 
1 BE
5
Für ein Rechteck mit den Seitenlängen  und
und  gilt:
gilt:
 und
und
 Berechne das Verhältnis der Längen der Rechteckseiten.
Berechne das Verhältnis der Längen der Rechteckseiten.
2 BE
6
Die Rappbodetalsperre hat die höchste Staumauer Deutschlands. In ihrer Nähe befindet sich die längste Doppelseilrutsche Europas. Hier können Mutige an einem  dicken Stahlseil eine Strecke von
dicken Stahlseil eine Strecke von  zurücklegen und dabei einen Höhenunterschied von
zurücklegen und dabei einen Höhenunterschied von  überwinden.
Berechne den Neigungswinkel dieser Doppelseilrutsche.
überwinden.
Berechne den Neigungswinkel dieser Doppelseilrutsche.
1 BE
7
Ein Quader ist  lang,
lang,  breit und
breit und  hoch.
Zeichne ein Netz dieses Quaders im Maßstab 1:50.
hoch.
Zeichne ein Netz dieses Quaders im Maßstab 1:50.
2 BE
8
Ein normaler Spielwürfel mit den Augenzahlen 1 bis 6 wird einmal geworfen.

a)
Gib die Wahrscheinlichkeit für das Werfen einer Augenzahl, die größer als 4 ist, an.
1 BE
Ein zweiter Würfel ist auf jeder Seite mit einem Buchstaben beschriftet. Der Buchstabe  wird mit einer Wahrscheinlichkeit von
wird mit einer Wahrscheinlichkeit von  gewürfelt.
gewürfelt.

b)
Gib die Anzahl der Seiten mit dem Buchstaben  an.
an.
1 BE
Ein weiterer Würfel ist wie im Bild beschriftet. Mit diesem wird zweimal nacheinander gewürfelt.
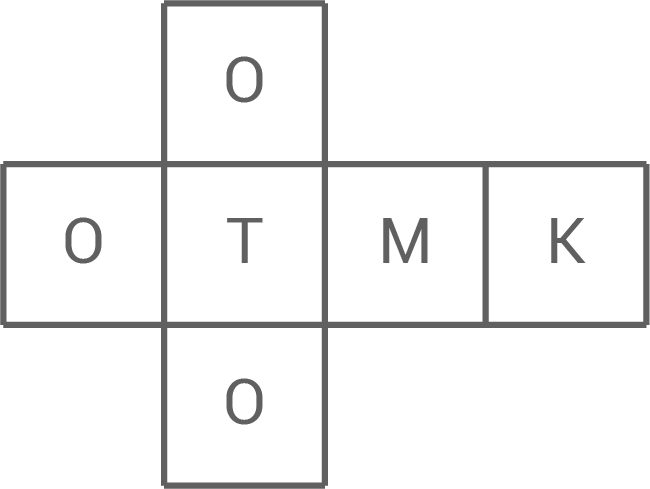

c)
Berechne die Wahrscheinlichkeit für die Buchstabenfolge „OK“.
1 BE
9
Kugelförmige Pralinen mit einem Durchmesser von  werden einzeln in quadratische Folienblätter eingewickelt. Der Flächeninhalt eines Blattes ist 2,5-mal so groß wie der Oberflächeninhalt einer Praline.
Berechne die Seitenlänge eines Folienblattes.
werden einzeln in quadratische Folienblätter eingewickelt. Der Flächeninhalt eines Blattes ist 2,5-mal so groß wie der Oberflächeninhalt einer Praline.
Berechne die Seitenlänge eines Folienblattes.
2 BE
1
a)
Es bietet sich ein Säulendiagramm an. Andere Diagramme sind jedoch auch möglich.

b)
Lösung mit der Lösungsformel


![\(\begin{array}[t]{rll}
p\,\%&=& \dfrac{W}{G}\cdot 100\,\% \\[5pt]
p\,\%&=& \dfrac{1\,443\,000\,\text{t}}{964\,000\,\text{t}}\cdot 100\,\% \\[5pt]
p\,\%&\approx& 149,7\,\%
\end{array}\)](https://www.schullv.de/resources/formulas/c2dab6f0a5c78c8009c6ecb4d3323513a2f729e409d323642da0925419bd3531_light.svg) Lösung mit Dreisatz
Die weltweite Produktion von Biokunststoffen ist auf
Lösung mit Dreisatz
Die weltweite Produktion von Biokunststoffen ist auf  gestiegen.
gestiegen.
c)
Der vierfache Wert der Produktion in 2012 beträgt:
 Dieser Wert soll ungefähr dem Wert ensprechen, der sich bei einer jährlichen Zunahme von
Dieser Wert soll ungefähr dem Wert ensprechen, der sich bei einer jährlichen Zunahme von  ergibt.
ergibt.


 Mit der Zinseszinsformel
Mit der Zinseszinsformel  folgt:
folgt:
![\(\begin{array}[t]{rll}
K_4&=& 1\,443\,000\,\text{t}\cdot \left(1+\dfrac{42\,\%}{100\,\%}\right)^4\\[5pt]
&=& 1\,443\,000\,\text{t}\cdot \left(1,42\right)^4\\[5pt]
&\approx& 5\,867\,049\,\text{t} \\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/9ff32fc44990bb02c3d97f1352f0dcfdf19a0da8dca0b39ba0d6ec37c7c09b69_light.svg) Das Ergebnis stimmt ungefähr mit dem vierfachen Wert des Wertes aus 2012 überein.
Das Ergebnis stimmt ungefähr mit dem vierfachen Wert des Wertes aus 2012 überein.
2
Die Länge der Strecke  lässt sich mit dem Kosinussatz berechnen.
Mit der Formel für den Flächeninhalt eines Dreiecks folgt für die Länge der Strecke
lässt sich mit dem Kosinussatz berechnen.
Mit der Formel für den Flächeninhalt eines Dreiecks folgt für die Länge der Strecke  Es muss gelten:
Es muss gelten:
![\(\begin{array}[t]{rll}
\overline{A B}&=&\dfrac{1}{2}\cdot \overline{DE} \\[5pt]
4,6\,\text{cm}&=&\dfrac{1}{2}\cdot 9,2\,\text{cm}\\[5pt]
4,6\,\text{cm}&=& 4,6\,\text{cm}\\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/4eb787efc736db7824bfed375bef9e89c912617a057ca8ef0b4cf478f99fa912_light.svg) Das angegebene Streckenverhältnis ist richtig.
Das angegebene Streckenverhältnis ist richtig.
3
Das Gleichungssystem kann mit dem Einsetzungsverfahren gelöst werden.
![\(\begin{array}[t]{lllllll}
\text{I}&y&+&3&=& x \\[5pt]
\text{II}&2y&+&4x&=& 6
\end{array}\)](https://www.schullv.de/resources/formulas/5c7283d078ec52d198267cf6eb13a3e6089200e34381c87d8d00fb4d5bec2676_light.svg) Umstellen der Gleichung
Umstellen der Gleichung  nach
nach  liefert:
liefert:
![\(\begin{array}[t]{rll}
y+3&=& x \quad \scriptsize \mid\;-3 \\[5pt]
y&=& x-3
\end{array}\)](https://www.schullv.de/resources/formulas/3d277affde92a9955d6c54cb7f0ec13258ebc8b01f2ceea95760d4fbb44fb78c_light.svg) Einsetzten von
Einsetzten von  in die Gleichung
in die Gleichung 
![\(\begin{array}[t]{rll}
2\cdot (x-3)+4x&=& 6 \\[5pt]
2x-6+4x&=& 6 \\[5pt]
6x-6&=& 6 \quad \scriptsize \mid\; +6\\[5pt]
6x&=& 12 \quad \scriptsize \mid\; :6\\[5pt]
x&=& 2
\end{array}\)](https://www.schullv.de/resources/formulas/e896d97a2512d43db4464bcc444c1431d6995abd2c71da6dfd9453f354cc098b_light.svg) Einsetzen von
Einsetzen von  in die Gleichung
in die Gleichung 
 Das Gleichungssystem hat die Lösung
Das Gleichungssystem hat die Lösung 
4
a)
Gesucht sind die Lösungen der Gleichung  Diese lassen sich mit der Lösungsformel berechnen.
Diese lassen sich mit der Lösungsformel berechnen.
![\(\begin{array}[t]{rll}
f(x)&=&x^2-6x+6 \\[5pt]
0&=&x^2-6x+6
\end{array}\)](https://www.schullv.de/resources/formulas/8e6a2ebb034b4ddd3b259b7e3cdebdd458f67c975aa1c72924be55a130a83959_light.svg) Es gilt
Es gilt  und
und 
![\(\begin{array}[t]{rll}
x_{1/2}&=& - \dfrac{p}{2} \pm \sqrt {\left( {\dfrac{p}{2}} \right)^2 - q}\\[5pt]
x_{1/2}&=& - \dfrac{-6}{2} \pm \sqrt {\left( {\dfrac{-6}{2}} \right)^2 - 6}\\[5pt]
x_{1/2}&=& 3 \pm \sqrt { 3^2 - 6}\\[5pt]
x_{1/2}&=& 3 \pm \sqrt {3}\\[5pt]
x_{1}&\approx& 3 + 1,7\\[5pt]
&=& 4,7\\[10pt]
x_{2}&=& 3 - 1,7\\[5pt]
&\approx& 1,3\\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/6f5cc1f3630d829c8ee69e8cd9b9dfc968c9ff9314f8fae370dde2b14c4bd434_light.svg) Die Funktion hat die Nullstellen
Die Funktion hat die Nullstellen  und
und 
b)
Bei der Funktion  handelt es sich um eine verschobene Normalparabel. Um diese grafisch darstellen zu können, wird der Scheitelpunkt berechnet:
handelt es sich um eine verschobene Normalparabel. Um diese grafisch darstellen zu können, wird der Scheitelpunkt berechnet:
 Es gilt
Es gilt  und
und 


 Für die Funktion
Für die Funktion  wird eine Wertetabelle angelegt.
wird eine Wertetabelle angelegt.
Damit können die beiden Funktionen in ein Koordinatensystem dargestellt werden.
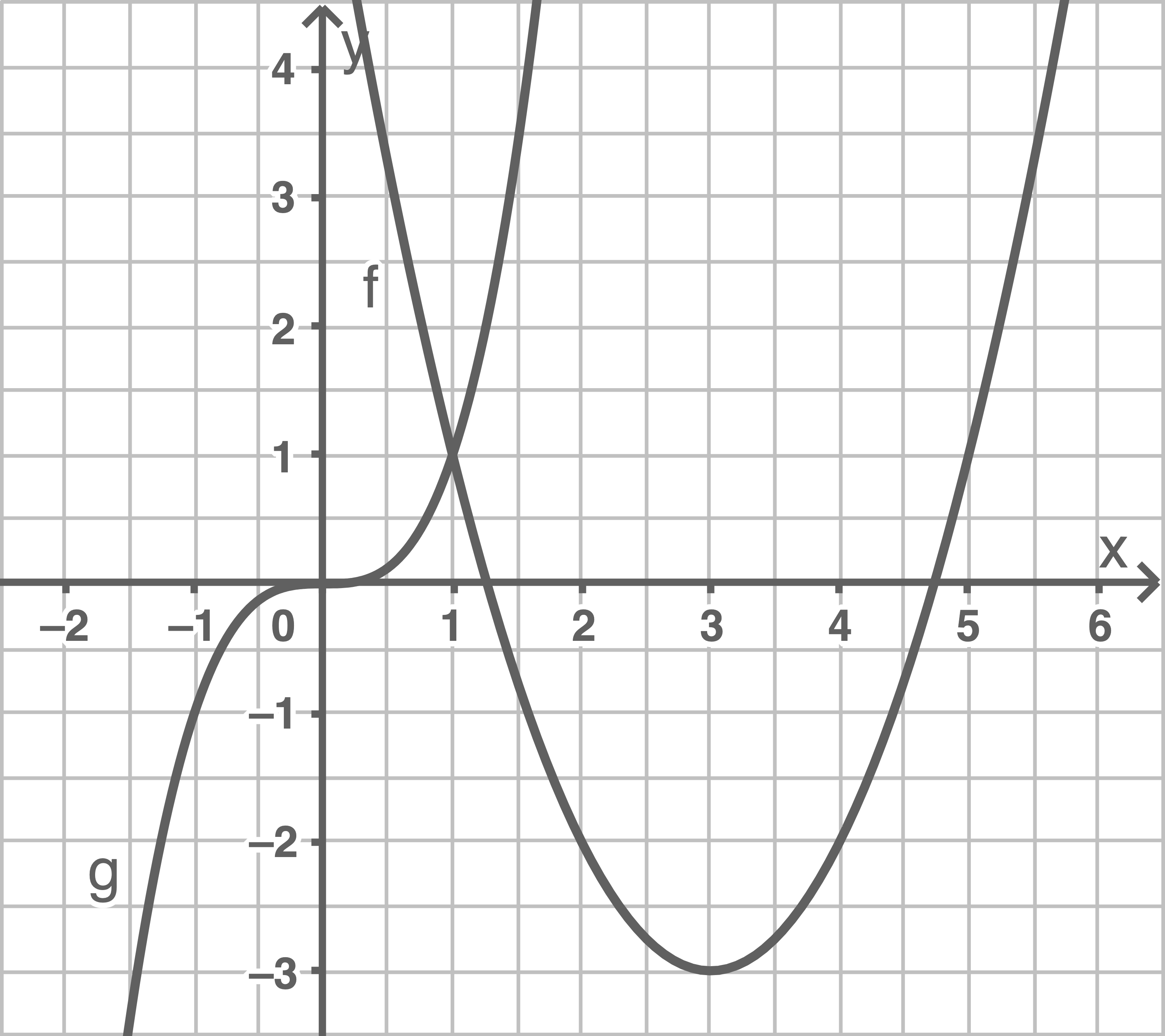
| -2 | -1 | 0 | 1 | 2 | |
| -8 | -1 | 0 | 1 | 8 |

c)
Die Längen der Strecken  und
und  lassen sich aus der Skizze ablesen.
lassen sich aus der Skizze ablesen.
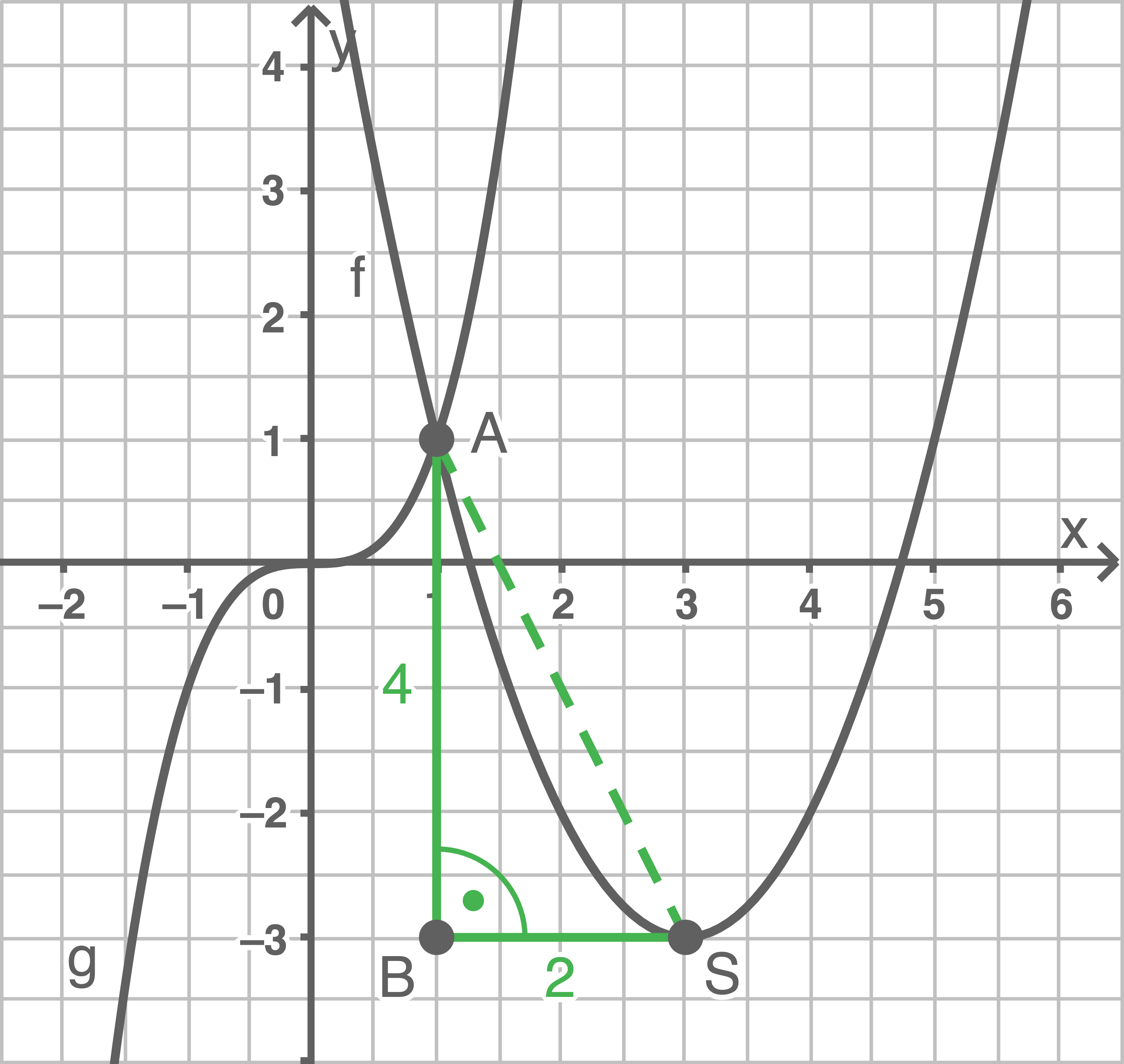

Skizze
Mit dem Satz des Pythagoras folgt für die Länge der Strecke 
![\(\begin{array}[t]{rll}
\overline{AS}^2&=& \overline{AB}^2+\overline{BS}^2 \\[5pt]
\overline{AS}^2&=& (4\,\text{cm})^2+(2\,\text{cm})^2 \\[5pt]
\overline{AS}^2&=& 20\,\text{cm}^2 \quad \scriptsize \mid\; \sqrt{\,} \\[5pt]
\overline{AS}&\approx& 4,5\,\text{cm}
\end{array}\)](https://www.schullv.de/resources/formulas/0ad6d2a8b8d58bda2778306590271016196b2bcf12917d249c25aa7948ae8b29_light.svg) Die Strecke
Die Strecke  ist ungefähr
ist ungefähr  lang.
lang.
5
Für den Flächeninhalt eines Rechtecks gilt  Einsetzen von
Einsetzen von  und
und  liefert:
liefert:
![\(\begin{array}[t]{rll}
128&=& a\cdot 2a^2 \\[5pt]
128&=& 2a^3 \quad \scriptsize \mid\; :2 \\[5pt]
64&=& a^3 \quad \scriptsize \mid\; \sqrt[3]{\,} \\[5pt]
4&=& a
\end{array}\)](https://www.schullv.de/resources/formulas/0845d4e3a668217714bb6b1d3651d3a778af628d6f893194d5316b9e474e1e3b_light.svg) Die Seite
Die Seite  ist
ist  lang. Damit gilt für die Länge der Seite
lang. Damit gilt für die Länge der Seite 
 Die Seite
Die Seite  ist
ist  lang. Damit folgt für das Verhältnis der beiden Rechteckseiten:
lang. Damit folgt für das Verhältnis der beiden Rechteckseiten:
 Das Verhältnis der Längen der Rechteckseiten beträgt
Das Verhältnis der Längen der Rechteckseiten beträgt 
6
Skizze des Sachverhalts:
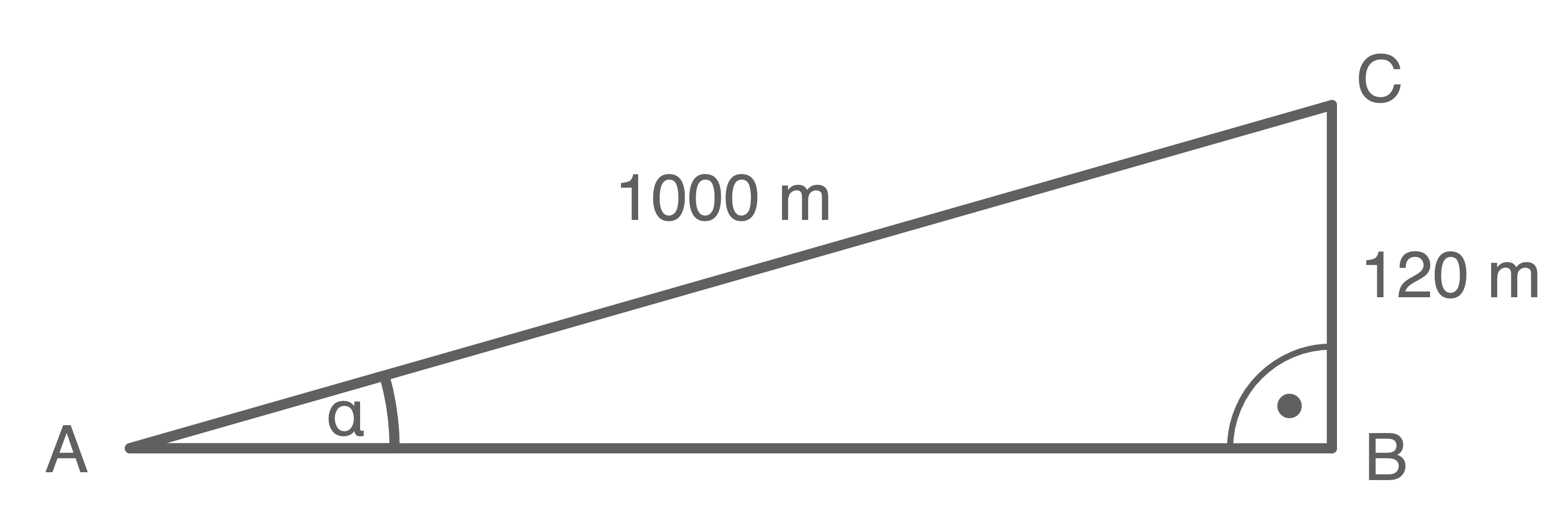 Der Neigungswinkel
Der Neigungswinkel  kann wie folgt berechnet werden:
kann wie folgt berechnet werden:
![\(\begin{array}[t]{rll}
\sin(\alpha)&=& \dfrac{\text{Gegenkathete}}{\text{Hypothenuse}} \\[5pt]
\sin(\alpha)&=&\dfrac{\overline{BC}}{\overline{AC}}\\[5pt]
\sin(\alpha)&=&\dfrac{120\,\text{m}}{1\,000\,\text{m}}\\[5pt]
\sin(\alpha)&=& 0,12 \quad \scriptsize \mid\; \sin^{-1}\\[5pt]
\alpha&\approx& 6,9°
\end{array}\)](https://www.schullv.de/resources/formulas/aab88acb7691a11bf1a3eca2fd8fd5d85050f51fed3e2bac248a71f48ac79f6d_light.svg) Die Größe des Neigungswinkels der Doppelseilrutsche beträgt ungefähr
Die Größe des Neigungswinkels der Doppelseilrutsche beträgt ungefähr 

7
Längen in der Zeichnung berechnen:


 Das Quadernetz kann nun mit den berechneten Seiten gezeichnet werden.
Das Quadernetz kann nun mit den berechneten Seiten gezeichnet werden.
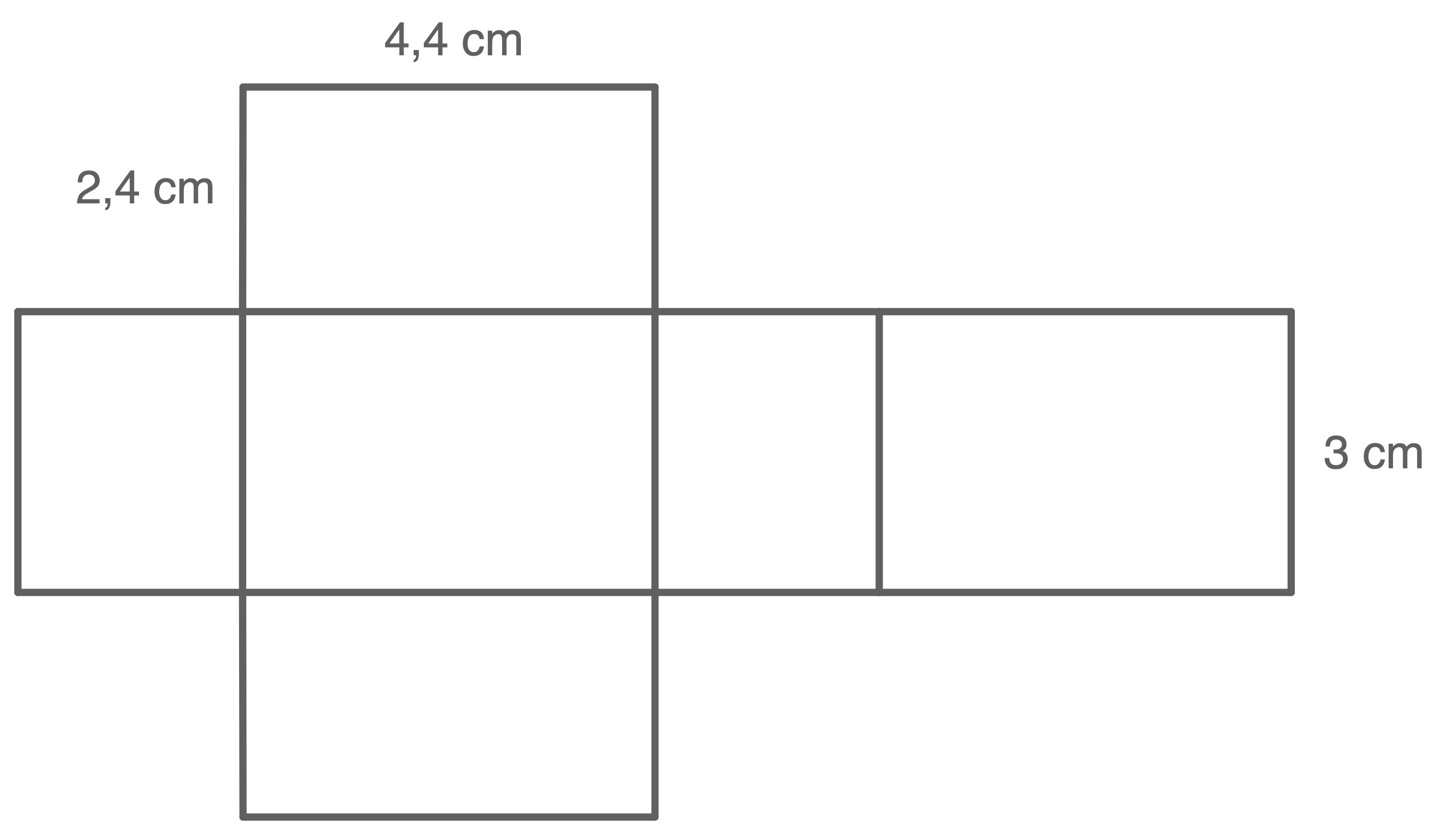 Je nach Bildschirmgröße kann die Messung variieren. Die Vorgehensweise bleibt jedoch die gleiche.
Je nach Bildschirmgröße kann die Messung variieren. Die Vorgehensweise bleibt jedoch die gleiche.

8
a)
6 mögliche Ergebnisse: 
2 günstige Ergebnisse:

![\(\begin{array}[t]{rll}
&=& \dfrac{\text{Anzahl günstiger Ergebnisse}}{\text{Anzahl möglicher Ergebnisse}}\\[5pt]
&=& \dfrac{2}{6} \\[5pt]
&=& \dfrac{1}{3}
\end{array}\)](https://www.schullv.de/resources/formulas/a56e9c1182c9c756f21122c03c5b9312175759be0eea02279767e21316b7a65a_light.svg) Die Wahrscheinlichkeit für das Ereignis „Augenzahl größer als 4 “ beträgt
Die Wahrscheinlichkeit für das Ereignis „Augenzahl größer als 4 “ beträgt  bzw.
bzw. 
2 günstige Ergebnisse:
b)
c)
9
Oberflächeninhalt einer Praline:
![\(\begin{array}[t]{rll}
A_P&=&4\cdot\pi\cdot r^2 \\[5pt]
A_P&=&4\cdot\pi\cdot (1,5\,\text{cm})^2 \\[5pt]
A_P&=& 28,3\,\text{cm}^2 \\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/284633f14cd5fa02edb3adbb34d552f93d45464f414487bfecda82deb09737c8_light.svg) Oberflächeninhalt eines Folienpapiers:
Oberflächeninhalt eines Folienpapiers:
![\(\begin{array}[t]{rll}
A_F&=& 2,5\cdot A_P \\[5pt]
&\approx& 2,5\cdot 28,3\,\text{cm}^2 \\[5pt]
&\approx& 70,8\,\text{cm}^2
\end{array}\)](https://www.schullv.de/resources/formulas/b33ba04345f6530eb1e557a4978d3a96f8edee2a0c6fdb9751a1b691a177f480_light.svg) Mit der Formel für den Oberflächeninhalt eines Quadrats folgt:
Mit der Formel für den Oberflächeninhalt eines Quadrats folgt:
![\(\begin{array}[t]{rll}
A_F&=& a^2 \\[5pt]
70,8\,\text{cm}^2&\approx& a^2 \quad \scriptsize \mid\; \sqrt{\,}\\[5pt]
8,4\,\text{cm}&\approx& a \\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/751d400a3f8d3e416ad4e5d334de4711cfafc88afe485a2936dd3c7af4a9577e_light.svg) Die Seitenlänge eines Folienblattes beträgt ungefähr
Die Seitenlänge eines Folienblattes beträgt ungefähr 