Wahlaufgaben
10
Wahlaufgabe Arithmetik/Algebra
10.1
Vereinfache diesen Term so weit wie möglich.

1 BE
10.2
Gegeben ist eine Gleichung eines linearen Gleichungssystems.
 Ermittle eine zweite Gleichung so, dass das Gleichungssystem die Lösung
Ermittle eine zweite Gleichung so, dass das Gleichungssystem die Lösung  hat.
hat.
2 BE
10.3
Drei Freunde kaufen gemeinsam ein Jahreslos für eine Lotterie.
Alex bezahlt 48 €. Ben beteiligt sich mit einem Drittel und Chris mit einem Sechstel am Lospreis.
Mit diesem Los gewinnen die drei Freunde Begründe, dass Alex bei gerechter Verteilung des Gewinnes
Begründe, dass Alex bei gerechter Verteilung des Gewinnes  erhält.
erhält.
Alex bezahlt 48 €. Ben beteiligt sich mit einem Drittel und Chris mit einem Sechstel am Lospreis.
Mit diesem Los gewinnen die drei Freunde
2 BE
10.4
Gegeben ist ein Zylinder mit dem Durchmesser  und ein zweiter Zylinder mit dem doppelten Durchmesser.
und ein zweiter Zylinder mit dem doppelten Durchmesser.
In beide Zylinder wird die gleiche Menge Flüssigkeit eingefüllt. Ermittle durch logische Überlegungen oder anhand eines selbstgewählten Beispiels das Verhältnis der beiden Höhen zueinander.
In beide Zylinder wird die gleiche Menge Flüssigkeit eingefüllt. Ermittle durch logische Überlegungen oder anhand eines selbstgewählten Beispiels das Verhältnis der beiden Höhen zueinander.
1 BE
11
Wahlaufgabe Funktionen
11.1
Gegeben ist die Funktion  mit
mit  Gib den Wertebereich dieser Funktion an.
Gib den Wertebereich dieser Funktion an.
1 BE
11.2
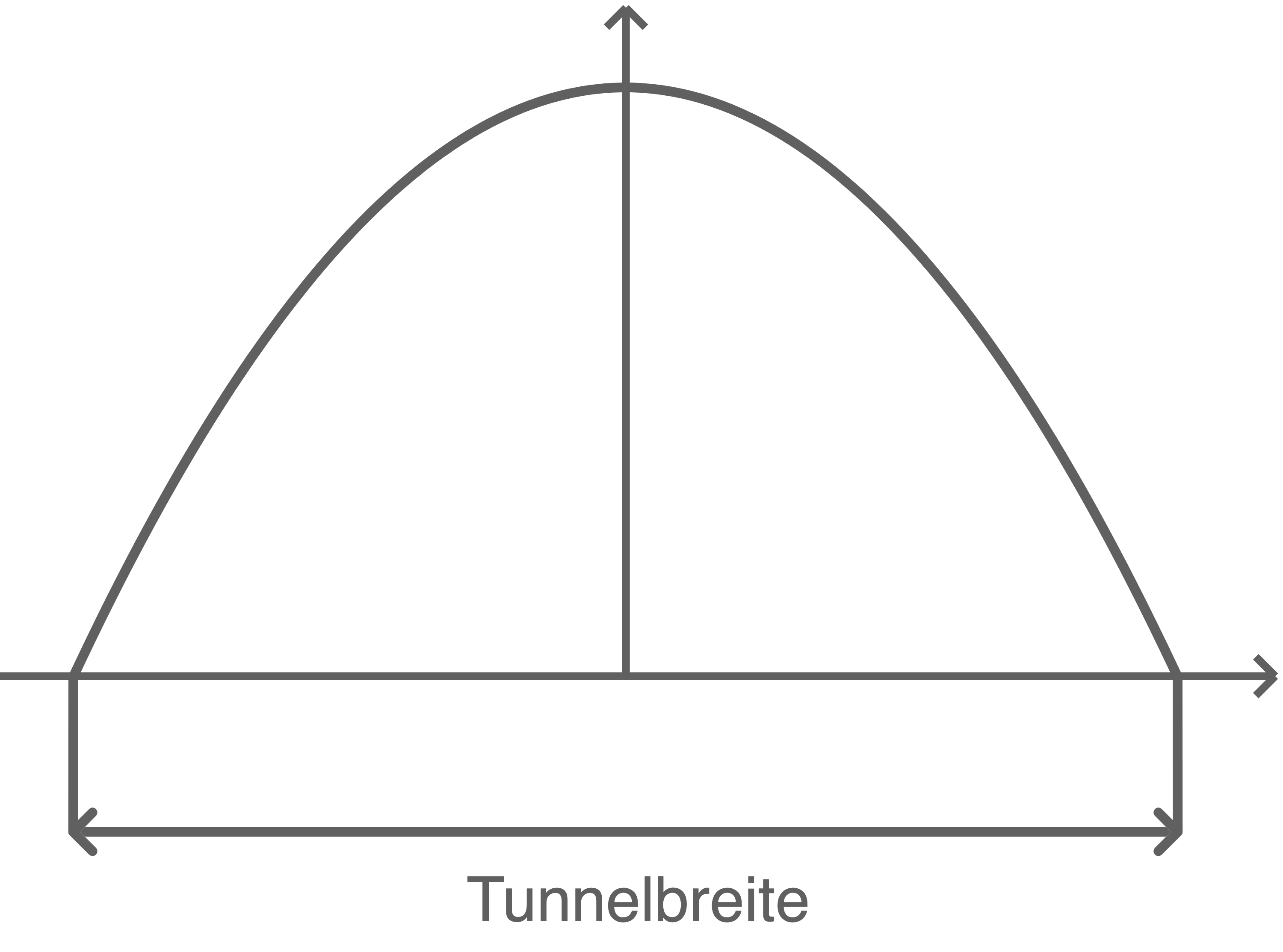
Der Querschnitt eines  hohen Tunnels hat annähernd die Form einer Parabel mit der Gleichung
hohen Tunnels hat annähernd die Form einer Parabel mit der Gleichung 
 zwischen Fahrzeug und Tunnelwand eingehalten werden kann.
Ein Lkw ist
zwischen Fahrzeug und Tunnelwand eingehalten werden kann.
Ein Lkw ist  breit und
breit und  hoch.
hoch.

Skizze nicht maßstäblich
a)
Berechne die Tunnelbreite.
Die Durchfahrt durch den Tunnel wird durch eine Ampel geregelt. Für einen Lkw ist die Durchfahrt nur erlaubt, wenn ein Mindestabstand von
2 BE
b)
Überprüfe, ob der Abstand zur Tunnelwand senkrecht nach oben für die gesamte Breite des Lkw eingehalten werden kann.
3 BE
12
Wahlaufgabe Geometrie
Hochbeete können aus witterungsbeständigen rechteckigen Kunststoffplatten als Seitenflächen aufgebaut werden.
Ein Set besteht aus acht Platten gleicher Länge 
Aus diesen Seitenflächen kann man unter anderem ein Beet mit einem regelmäßigen Achteck als Grundfläche bauen.
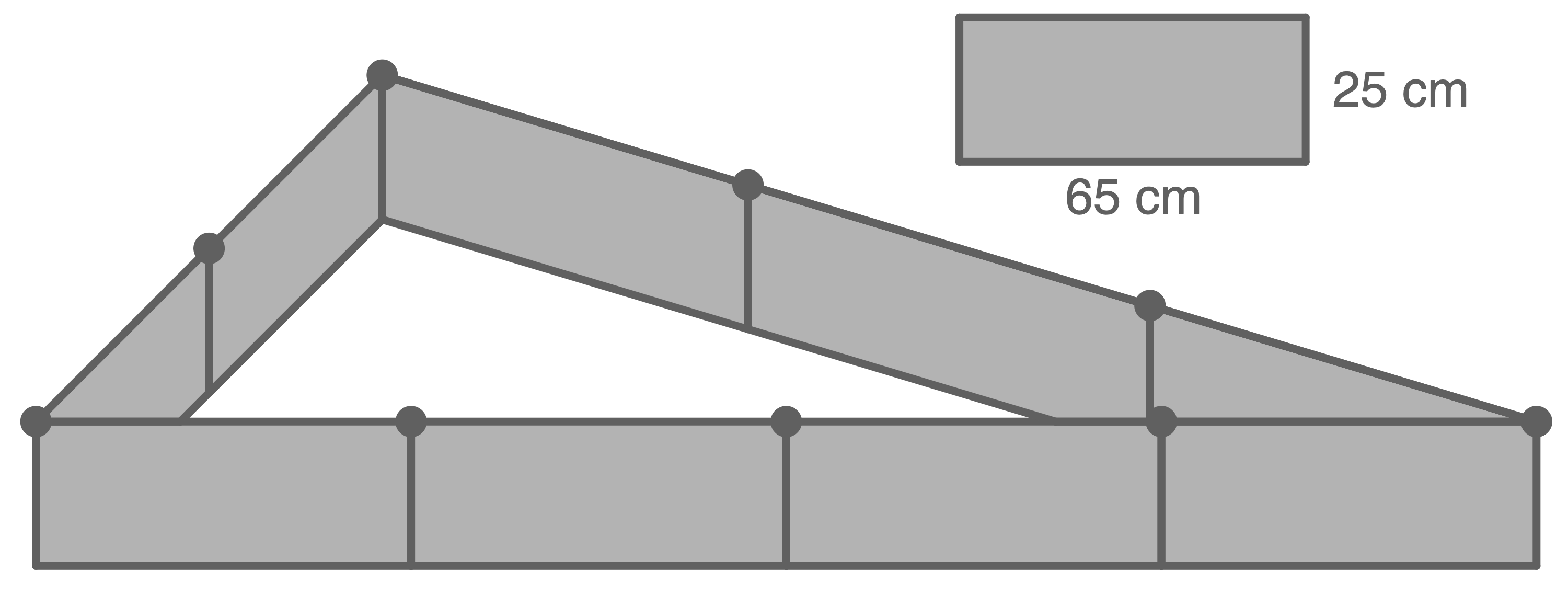 Das Beet soll vollständig mit Erde befüllt werden.
Das Beet soll vollständig mit Erde befüllt werden.
Aus diesen Seitenflächen kann man unter anderem ein Beet mit einem regelmäßigen Achteck als Grundfläche bauen.
a)
Berechne für eine selbstgewählte Plattenlänge  den Flächeninhalt dieser Grundfläche.
den Flächeninhalt dieser Grundfläche.
Überprüfe, ob die gegebene Gleichung für die gewählte Plattenlänge auch zur Berechnung genutzt werden kann.
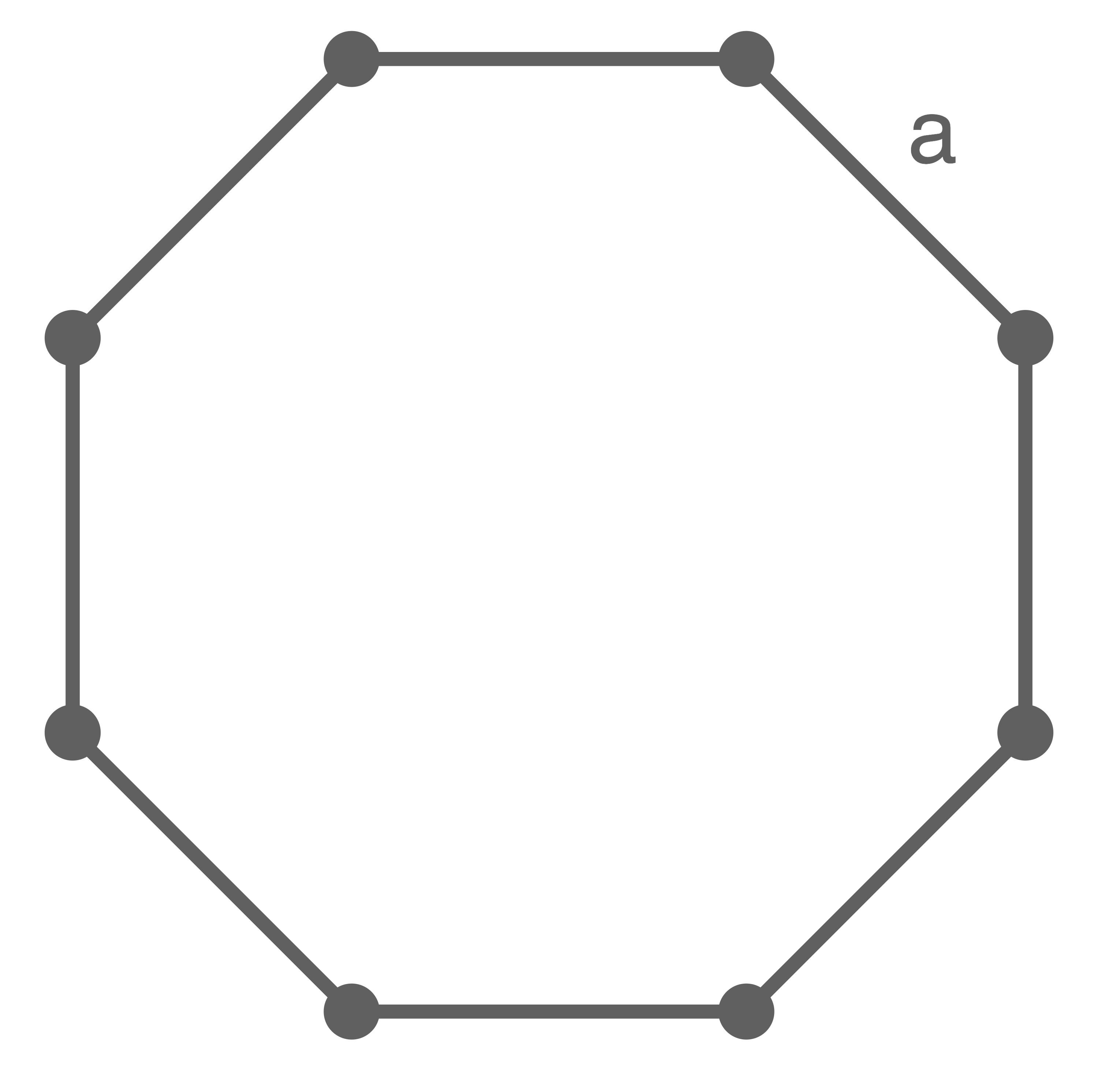

Herr Meier hat in seinem Garten ein dreieckiges Hochbeet aus 9 Platten aufgebaut.
Überprüfe, ob die gegebene Gleichung für die gewählte Plattenlänge auch zur Berechnung genutzt werden kann.

3 BE

Skizze nicht maßstäblich
b)
Berechne das Volumen der benötigten Erde.
3 BE
13
Wahlaufgabe Stochastik
13.1
In der Tabelle ist die Notenverteilung einer Leistungskontrolle erfasst.
| Note | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|
| Anzahl der Schüler | 3 | 3 | 2 | 5 | 2 | 0 |
a)
Berechne den Notendurchschnitt dieser Leistungskontrolle.
Peter muss die Leistungskontrolle nachschreiben. Durch seine Note ändert sich der Notendurchschnitt. Der Median bleibt gleich.
1 BE
b)
Gib die Note an, die Peter erhalten haben könnte.
1 BE
13.2
Tom und Anne haben sich unterschiedliche Spielwürfel gebastelt.
Tom


Anne


a)
Mit welcher Wahrscheinlichkeit würfelt Tom keine „6“?
Sie vereinbaren folgende Spielregel: Jeder würfelt einmal mit seinem Würfel. Es gewinnt derjenige, der die höhere Augenzahl hat.
1 BE
b)
Zeichne ein dazugehöriges Baumdiagramm.
Zeige, dass Tom und Anne mit der gleichen Wahrscheinlichkeit gewinnen können.
Zeige, dass Tom und Anne mit der gleichen Wahrscheinlichkeit gewinnen können.
3 BE
10.1
10.2
Einsetzen der Lösung  in die allgemeine Gleichung
in die allgemeine Gleichung 
![\(\begin{array}[t]{rll}
2&=& m\cdot 1+n &\quad \scriptsize \mid\; -n \\[5pt]
2-n&=& m
\end{array}\)](https://www.schullv.de/resources/formulas/c0472ef9c7e1b02b39e4fa97341c8d0d9b0ac8805716d781e2a748d84a6b54a9_light.svg) Durch Festlegen eines Wertes von
Durch Festlegen eines Wertes von  kann der zugehörige Wert
kann der zugehörige Wert  berechnet werden.
Mögliche Werte sind zum Beispiel
berechnet werden.
Mögliche Werte sind zum Beispiel  und
und  Eine zweite Gleichung, mit der das Gleichungssystem die Lösung
Eine zweite Gleichung, mit der das Gleichungssystem die Lösung  hat, ist also die folgende:
hat, ist also die folgende:

10.3
Zunächst wird Alex' Anteil am Lospreis berechnet:
![\(\begin{array}[t]{rll}
1-\dfrac{1}{3}-\dfrac{1}{6} &=& \dfrac{6}{6}-\dfrac{2}{6}-\dfrac{1}{6} \\[5pt]
&=& \dfrac{3}{6}\\[5pt]
&=& \dfrac{1}{2}
\end{array}\)](https://www.schullv.de/resources/formulas/54efed5d811af9feab5aa0b1ae9d35c7e263df7e9482813318be80c1eb343c8a_light.svg) Da Alex die Hälfte des Lospreises gezahlt hat, bekommt er bei gerechter Verteilung auch die Hälfte des Gewinns.
Da Alex die Hälfte des Lospreises gezahlt hat, bekommt er bei gerechter Verteilung auch die Hälfte des Gewinns.
 Bei gerechter Verteilung erhält Alex
Bei gerechter Verteilung erhält Alex 
10.4
Maße des schmalen Zylinders:
Radius: Volumen:
Volumen:  Höhe:
Höhe:  Maße des breiten Zylinders:
Maße des breiten Zylinders:
Radius: Volumen:
Volumen:  Höhe:
Höhe:  Für die Volumina der beiden Zylinder gilt:
Für die Volumina der beiden Zylinder gilt:
![\(\begin{array}[t]{rll}
V_1&=& V_2 \\[5pt]
\pi\cdot r_1^2\cdot h_1&=& \pi\cdot r_2^2\cdot h_2 \quad \scriptsize \mid\; r_2=2\cdot r_1\\[5pt]
\pi\cdot r_1^2\cdot h_1&=& \pi\cdot (2\cdot r_1)^2\cdot h_2 \\[5pt]
\pi\cdot r_1^2\cdot h_1&=& \pi\cdot 4\cdot r_1^2 \cdot h_2 \quad \scriptsize \mid\; :(\pi\cdot r_1^2) \\[5pt]
h_1&=& 4\cdot h_2 \quad \scriptsize \mid\; :h_2 \\[5pt]
\dfrac{h_1}{h_2}&=& \dfrac{4}{1}
\end{array}\)](https://www.schullv.de/resources/formulas/68205d52bce35bae1b9eb6b2fba6e9447d8562e38287550fc6798285f6bc6d21_light.svg) Die Höhe
Die Höhe  steht zur Höhe
steht zur Höhe  im Verhältnis
im Verhältnis 
Radius:
Radius:
11.1
Da der Faktor vor dem  positiv ist, gilt folgende Abschätzung:
positiv ist, gilt folgende Abschätzung:
 Damit ist der Wertebereich gegeben durch
Damit ist der Wertebereich gegeben durch  mit
mit 
11.2
a)
Um die Breite des Tunnels zu berechnen, werden zunächst die Nullstellen der Parabel berechnet.
![\(\begin{array}[t]{rll}
f(x)&=& -0,3x^2+3,8 \\[5pt]
0&=& -0,3x^2+3,8 \quad \scriptsize \mid\; -3,8 \\[5pt]
-3,8&=& -0,3x^2 \quad \scriptsize \mid\; :(-0,3) \\[5pt]
12,67&=& x^2 \quad \scriptsize \mid\; \sqrt{\,} \\[5pt]
\pm3,6&\approx& x \\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/509ec2da0aaff3588d6eb17be195d94320f9efa1de48b87157ab131595abb5ef_light.svg) Die Parabel hat die Nullstellen
Die Parabel hat die Nullstellen  und
und  Die Breite des Tunnels ist nun durch den Abstand der beiden Nullstellen voneinander gegeben.
Die Breite des Tunnels ist nun durch den Abstand der beiden Nullstellen voneinander gegeben.
 Der Tunnel ist ungefähr
Der Tunnel ist ungefähr  breit.
breit.
b)
Der geringste Abstand zwischen Lkw und Tunneldecke wird an den Rändern des LKWs, also bei  sein. Aus Symmetriegründen muss nur eine Seite überprüft werden.
Höhe des Tunnels am Rand des Lkws:
sein. Aus Symmetriegründen muss nur eine Seite überprüft werden.
Höhe des Tunnels am Rand des Lkws:
![\(\begin{array}[t]{rll}
f(1,15)&=& -0,3\cdot (1,15)^2+3,8 \\[5pt]
f(1,15)&=& 3,40 \\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/e8271372715110783a5c3b98ec07bc6d8cdd052a728065bd3287849f0e484a40_light.svg) Abstand des Lkws zu Tunneldecke:
Abstand des Lkws zu Tunneldecke:
 Der Abstand zwischen LKW und Tunneldecke beträgt
Der Abstand zwischen LKW und Tunneldecke beträgt  Der nötige Mindestabstand von
Der nötige Mindestabstand von  ist damit eingehalten.
ist damit eingehalten.
12
a)
Flächeninhalt der Grundfläche berechnen

![\(\begin{array}[t]{rll}
\dfrac{b}{\sin \beta}&=& \dfrac{a}{\sin \alpha} \quad \scriptsize \mid\; \cdot \sin \beta\\[5pt]
b&=& \dfrac{a}{\sin \alpha}\cdot \sin \beta \\[5pt]
b&=& \dfrac{1\,\text{m}}{\sin 45°}\cdot \sin 67,5° \\[5pt]
b&\approx& 1,3\,\text{m}
\end{array}\)](https://www.schullv.de/resources/formulas/3ca5909c44c9d49d5d1e7477b8a71cb65c291770551739782410857dfc53783f_light.svg) Damit kann nun der Flächeninhalt eines Dreiecks berechnet werden:
Damit kann nun der Flächeninhalt eines Dreiecks berechnet werden:
![\(\begin{array}[t]{rll}
A_D&=& \dfrac{1}{2}\cdot a\cdot b\cdot \sin \beta \\[5pt]
&\approx& \dfrac{1}{2}\cdot 1\,\text{m}\cdot 1,3\,\text{m}\cdot \sin 67,5° \\[5pt]
&\approx& 0,6\,\text{m}^2
\end{array}\)](https://www.schullv.de/resources/formulas/68bee14d230eb9356c5a81a9dec69d6a7c677185b0b1101195729bf5c0ed3fa4_light.svg) Für den Flächeninhalt des Achtecks folgt:
Für den Flächeninhalt des Achtecks folgt:
 Überprüfen, ob Gleichung genutzt werden kann
Mit der Formel ergibt sich der folgende Flächeninhalt für
Überprüfen, ob Gleichung genutzt werden kann
Mit der Formel ergibt sich der folgende Flächeninhalt für 
![\(\begin{array}[t]{rll}
A&=& \dfrac{2a^2}{\tan(22,5°)} \\[5pt]
&=& \dfrac{2\cdot(1\,\text{m})^2}{\tan(22,5°)}\\[5pt]
&\approx& 4,8\,\text{m}^2
\end{array}\)](https://www.schullv.de/resources/formulas/3792ec2f3ca5fa891b4254be36feeb0491c4d54ffde784721b96ccf3ace27368_light.svg) Die Ergebnisse sind gleich. Die angegebene Formel kann dazu verwendet werden, den Flächeninhalt eines Achtecks zu berechnen.
Die Ergebnisse sind gleich. Die angegebene Formel kann dazu verwendet werden, den Flächeninhalt eines Achtecks zu berechnen.
Hier wird beispielhaft die Kantenlänge  gewählt.
gewählt.
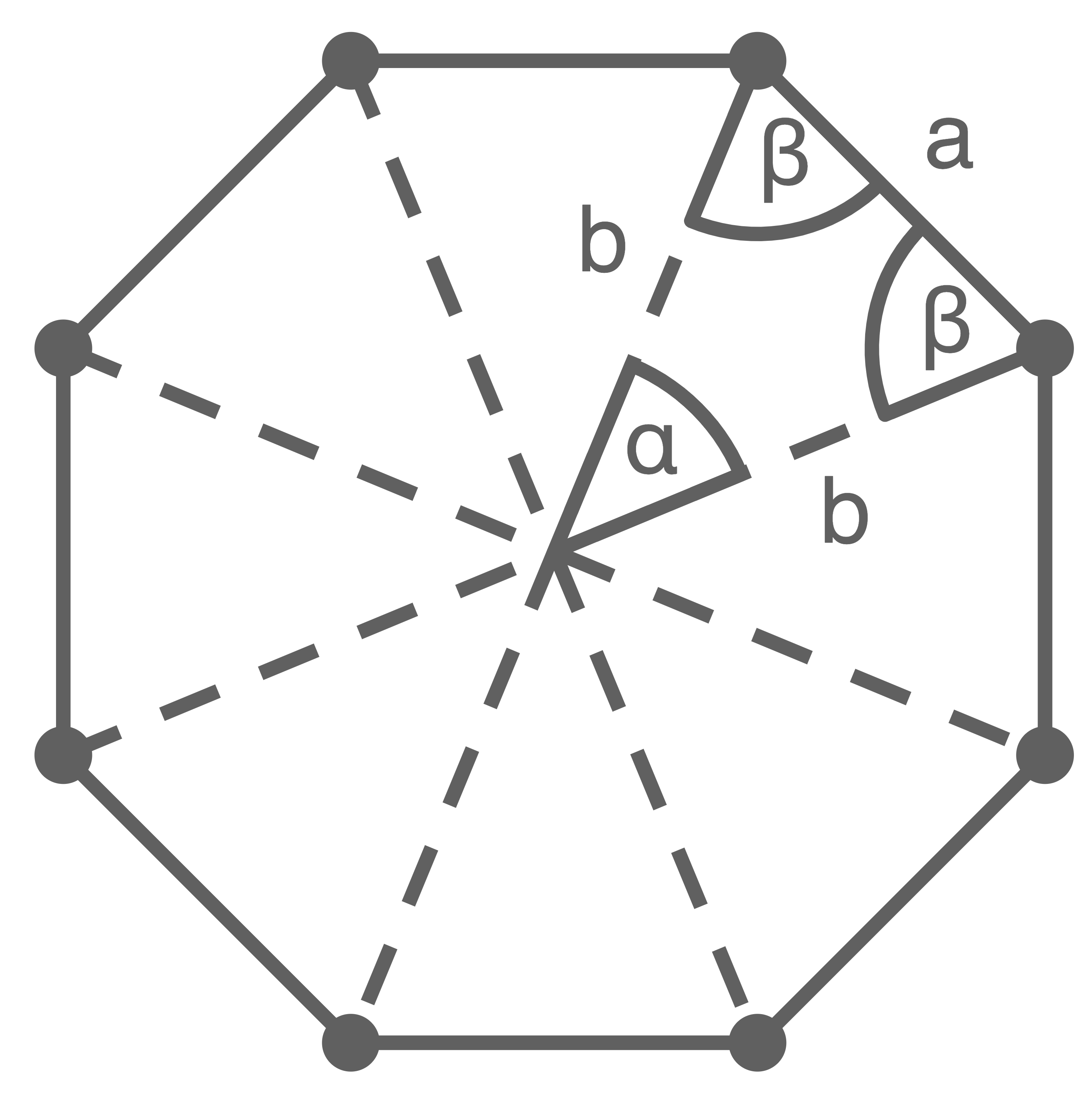 Berechnung des Winkels
Berechnung des Winkels 
 Da die Dreiecke in der Skizze gleichschenklig sind, folgt mit der Innenwinkelsumme eines Dreiecks:
Da die Dreiecke in der Skizze gleichschenklig sind, folgt mit der Innenwinkelsumme eines Dreiecks:

Mit dem Sinussatz gilt für die Länge der Seite 
b)
Bei dem Beet handelt es sich um ein Prisma mit dreieckiger Grundfläche. Um das Volumen zu berechnen, wird zunächst der Flächeninhalt der Grundfläche benötigt.
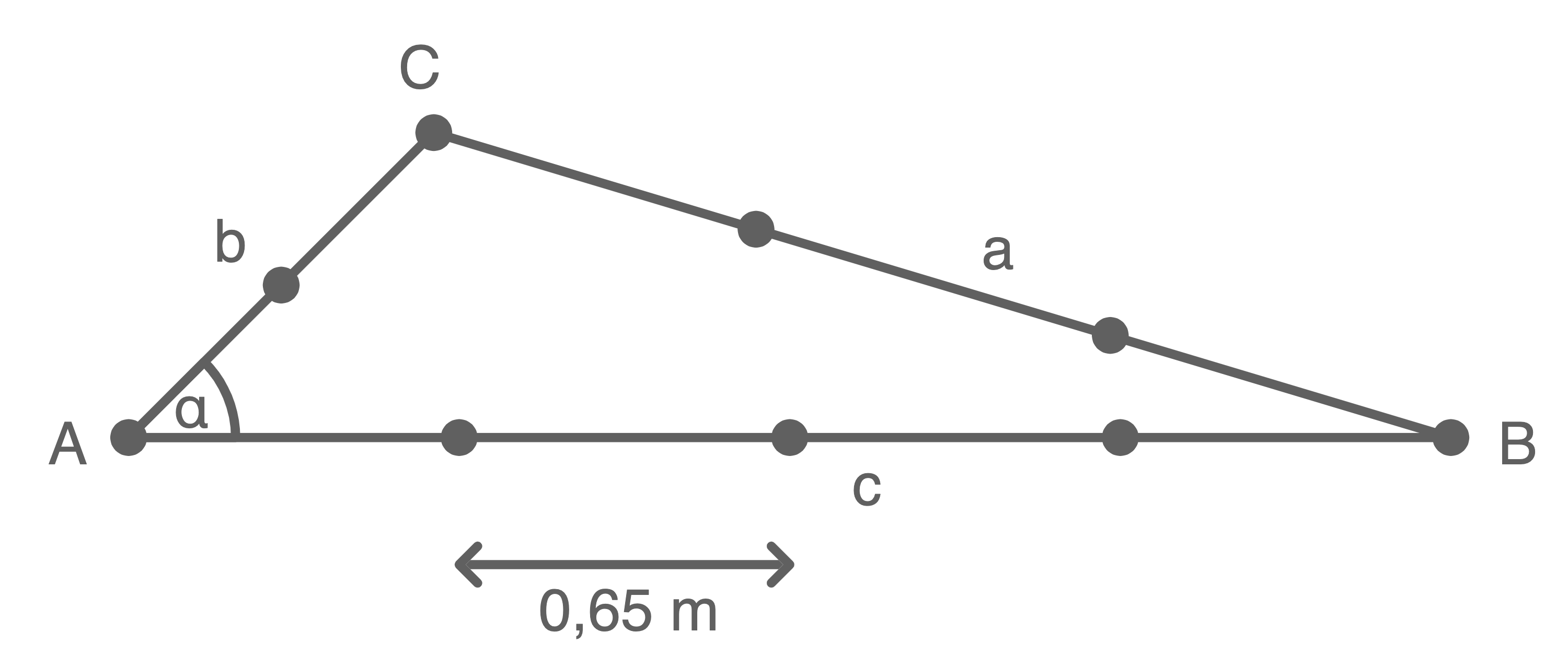 Seite
Seite  besteht aus
besteht aus  Platten, Seite
Platten, Seite  aus
aus  Platten und Seite
Platten und Seite  aus
aus  Platten. Jede Platte ist
Platten. Jede Platte ist  lang.
lang.


 Berechne den Winkel
Berechne den Winkel  mit dem Kosinussatz.
Damit lässt sich der Flächeninhalt der dreieckigen Grundfläche des Prismas berechnen:
mit dem Kosinussatz.
Damit lässt sich der Flächeninhalt der dreieckigen Grundfläche des Prismas berechnen:
![\(\begin{array}[t]{rll}
A_D&=& \dfrac{1}{2}\cdot b\cdot c\cdot \sin \alpha \\[5pt]
&\approx& \dfrac{1}{2}\cdot 1,30\,\text{m} \cdot 2,60\,\text{m} \cdot \sin 46,6° \\[5pt]
&\approx& 1,2\,\text{m}^2
\end{array}\)](https://www.schullv.de/resources/formulas/7b38668a216630da6c6ffe37cdadbe62fa8e982ea9d1c546f07f0192f6980029_light.svg) Für das Volumen des Prismas mit der Höhe
Für das Volumen des Prismas mit der Höhe  folgt:
folgt:
![\(\begin{array}[t]{rll}
V&=& A_D\cdot h \\[5pt]
&=& 1,2\,\text{m}^2 \cdot 0,25\,\text{m} \\[5pt]
&=& 0,3\,\text{m}^3 \\[5pt]
&=& 300\,\text{dm}^3
\end{array}\)](https://www.schullv.de/resources/formulas/cb80858a8d5deaf797fdd644aed088702dd58a9b4d7f97b707f3517206847f2c_light.svg) Herr Meier benötigt
Herr Meier benötigt  Erde, um das Beet zu befüllen.
Erde, um das Beet zu befüllen.

13.1
a)
b)
Zunächst muss der Median bestimmt werden:
1 1 1 2 2 2 3 3 4 4 4 4 4 5 5
Der Median beträgt 3. Wenn die Anzahl an Messwerten eine gerade Zahl ist, dann ist der Median der Mittelwert der beiden mittleren Werte.
Hätte Peter eine Note schlechter als 3 geschrieben, würde der Median aus dem Mittelwert von 3 und 4 gebildet werden und sich damit verändern.
Eine 3 kann Peter nicht geschrieben haben, weil seine Note den Durchschnitt verändert hat.
Peter muss also eine 1 oder 2 geschrieben haben.
13.2
a)
6 mögliche Ergebnisse: 
5 günstige Ergebnisse:
![\(\begin{array}[t]{rll}
& P(\text{keine „6“}) \\[5pt]
=& \dfrac{\text{Anzahl günstiger Ergebnisse}}{\text{Anzahl möglicher Ergebnisse}} \\[5pt]
=& \dfrac{5}{6}
\end{array}\)](https://www.schullv.de/resources/formulas/df02dba29300fb53a9edcd75c8277473064cc4a876636eaed14b775708d3b140_light.svg) Die Wahrscheinlichkeit, dass Tom keine 6 Würfelt, beträgt
Die Wahrscheinlichkeit, dass Tom keine 6 Würfelt, beträgt 
5 günstige Ergebnisse:
b)
Baumdiagramm zeichnen
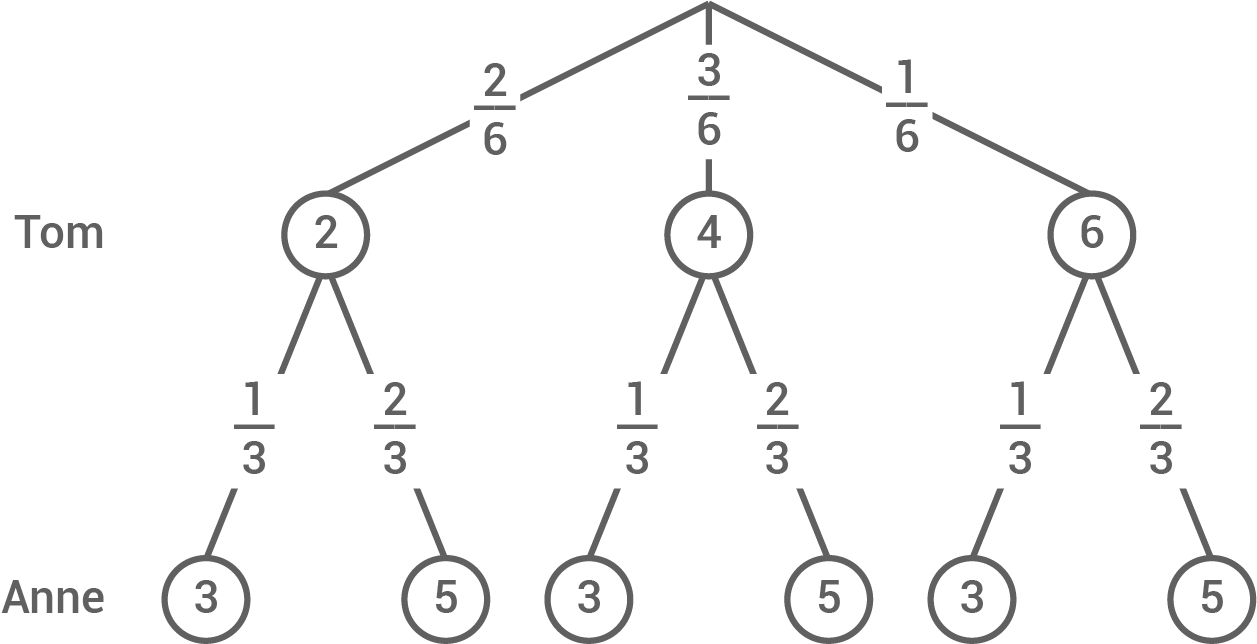 Gleiche Gewinnwahrscheinlichkeit zeigen
Wahrscheinlichkeit für die Pfade, bei denen Anne das Spiel gewinnt:
Gleiche Gewinnwahrscheinlichkeit zeigen
Wahrscheinlichkeit für die Pfade, bei denen Anne das Spiel gewinnt:


 In der Summe ergibt das für Annes Sieg die folgende Wahrscheinlichkeit:
In der Summe ergibt das für Annes Sieg die folgende Wahrscheinlichkeit:
 Wenn Anne mit der Wahrscheinlichkeit
Wenn Anne mit der Wahrscheinlichkeit  gewinnt, dann gewinnt auch Tom mit der Wahrscheinlichkeit
gewinnt, dann gewinnt auch Tom mit der Wahrscheinlichkeit  Die Wahrscheinlichkeiten für einen Sieg sind daher für beide gleich.
Die Wahrscheinlichkeiten für einen Sieg sind daher für beide gleich.
