Wahlaufgaben
9
Wahlaufgabe Trigonometrie
9.1
Zwei Aussagen sind wahr. Gib diese an.
- Jedes Rechteck hat vier Symmetrieachsen.
- In jedem Rechteck halbieren die Diagonalen die Innenwinkel.
- In jedem Rechteck sind die Diagonalen gleich lang.
- Es gibt Rechtecke mit vier gleich langen Seiten.
2 BE
9.2
Alex und Benno gehen in dieselbe Schule.
Beide benötigen für den Weg zur Schule 15 Minuten.
Alex fährt mit dem Fahrrad und schafft drei Kilometer in zehn Minuten.
Benno benutzt den Schulbus, der mit einer Durchschnittsgeschwindigkeit von fährt.
fährt.
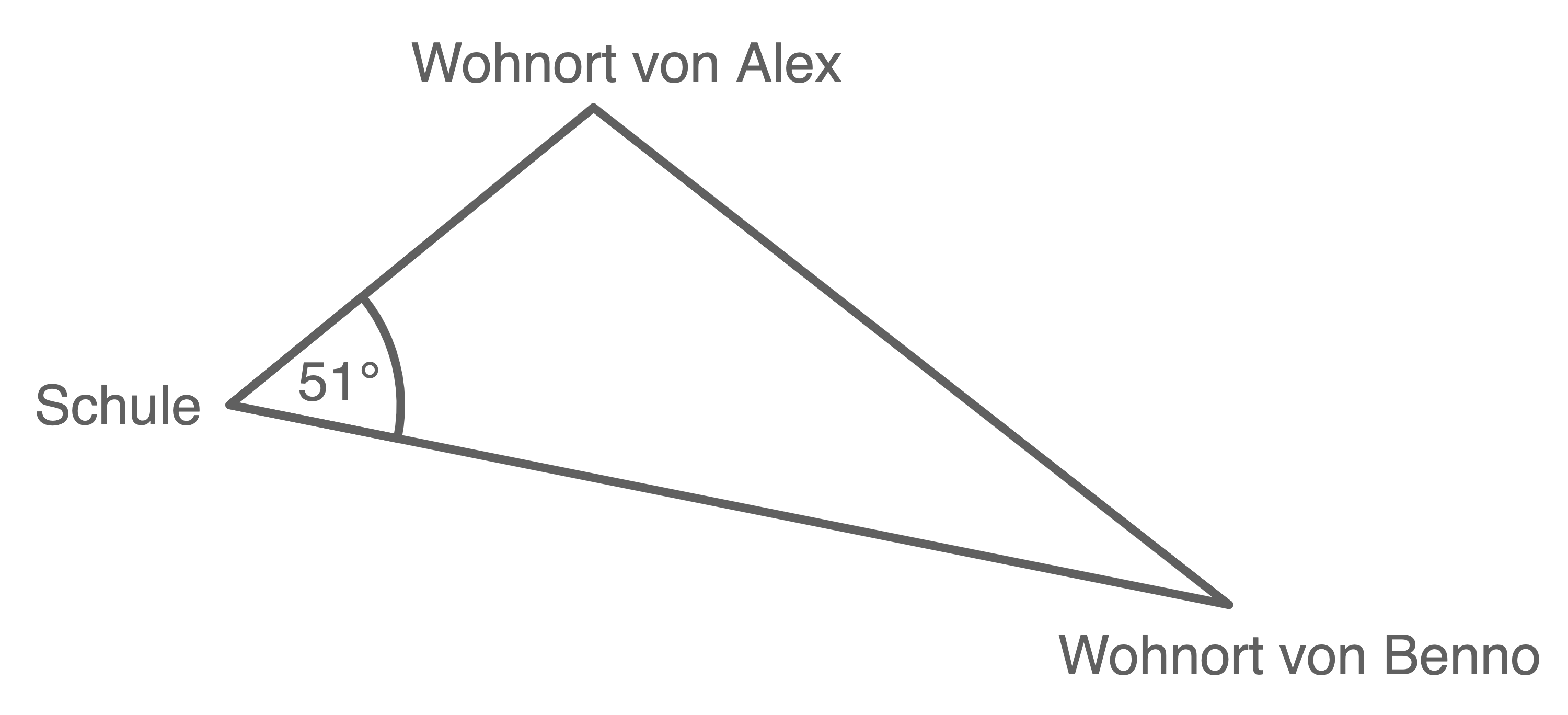 Berechne die Länge der Straße zwischen den beiden Wohnorten.
Berechne die Länge der Straße zwischen den beiden Wohnorten.
Beide benötigen für den Weg zur Schule 15 Minuten.
Alex fährt mit dem Fahrrad und schafft drei Kilometer in zehn Minuten.
Benno benutzt den Schulbus, der mit einer Durchschnittsgeschwindigkeit von

Skizze nicht maßstäblich
2 BE
9.3
Ein fünfeckiges Waldstück ist  groß.
groß.
Ein Teil davon wird neu bepflanzt.
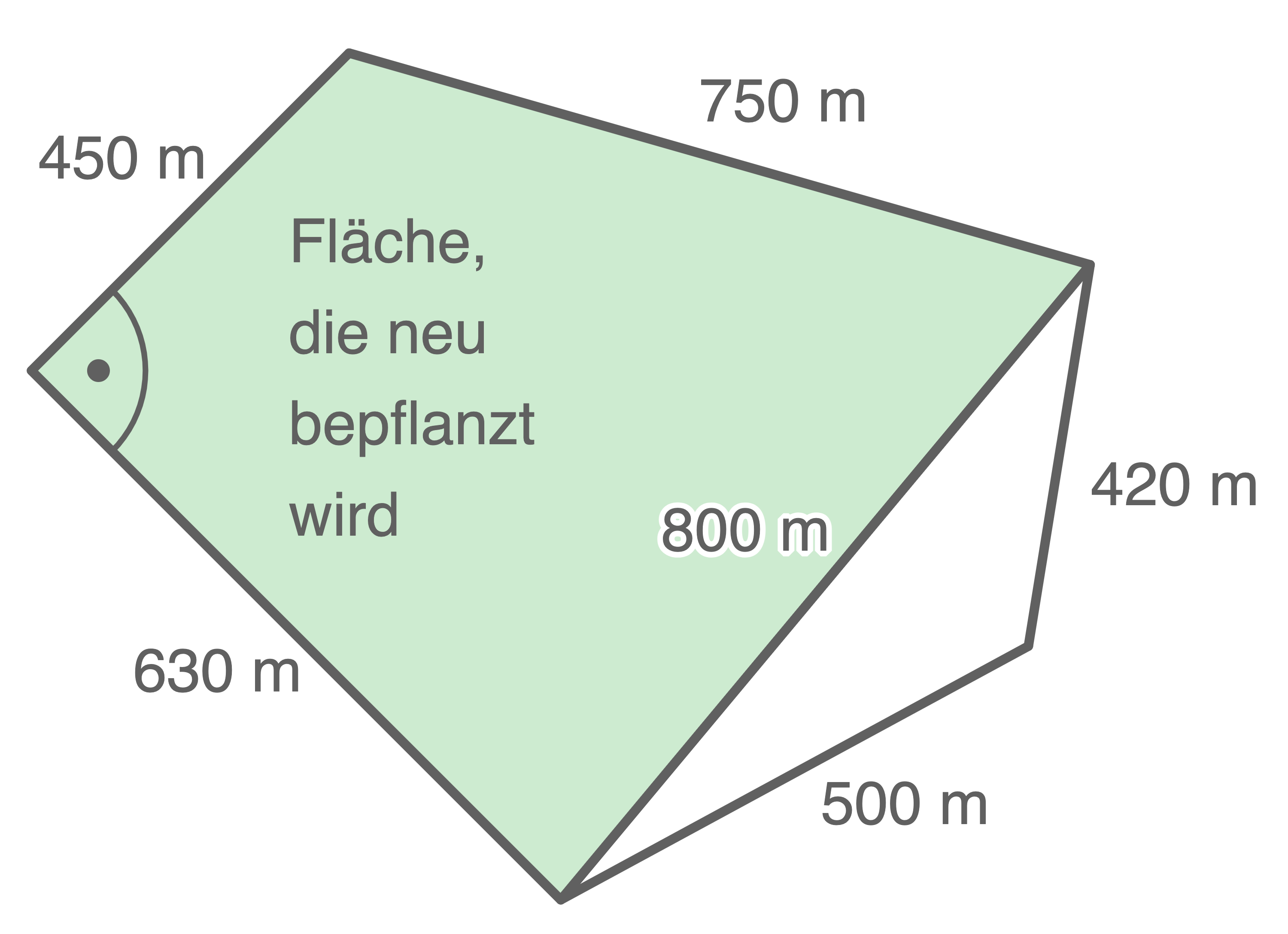
Ein Teil davon wird neu bepflanzt.

Skizze nicht maßstäblich
a)
Berechne den Flächeninhalt der Fläche, die neu bepflanzt wird.
Gib diesen Flächeninhalt in Hektar an.
Gib diesen Flächeninhalt in Hektar an.
4 BE
b)
Zeichne die Fläche, die neu bepflanzt wird, in einem geeigneten Maßstab.
2 BE
9.4
Zwischen zwei parallelen Geraden liegen ein Dreieck und ein Trapez.
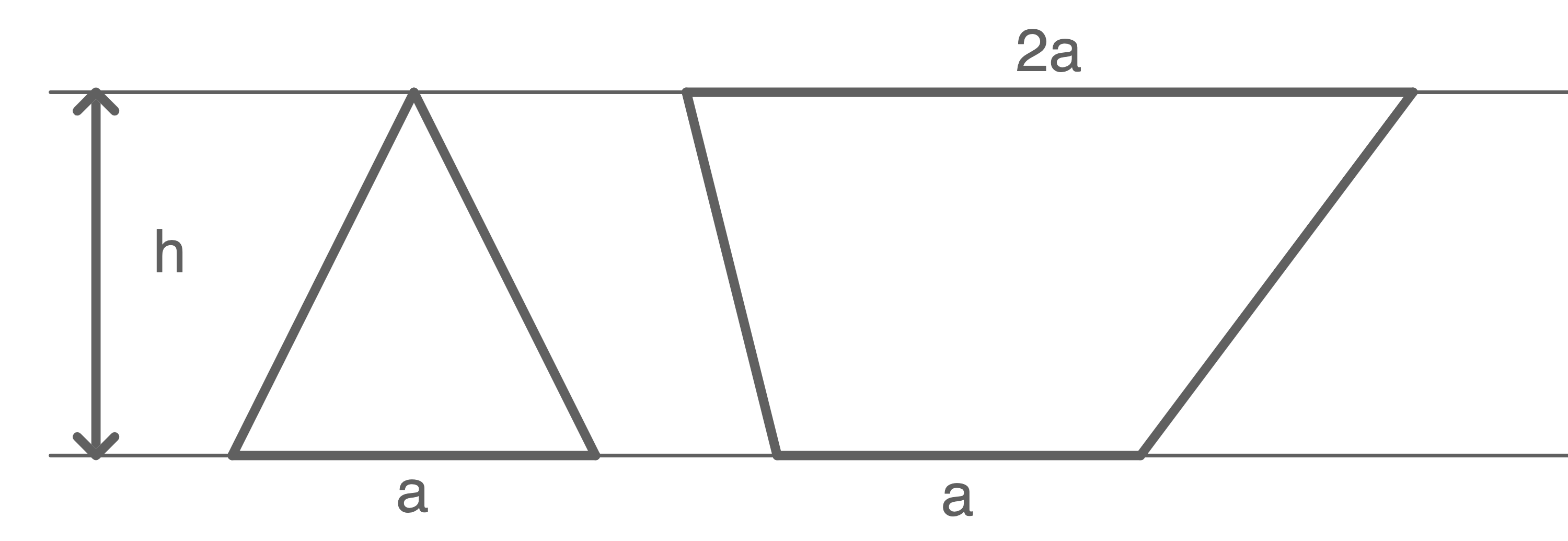 Weise mithilfe eines selbstgewählten Beispiels rechnerisch oder durch logische Schlussfolgerungen nach, dass der Flächeninhalt des Trapezes dreimal so groß ist wie der Flächeninhalt des Dreiecks.
Weise mithilfe eines selbstgewählten Beispiels rechnerisch oder durch logische Schlussfolgerungen nach, dass der Flächeninhalt des Trapezes dreimal so groß ist wie der Flächeninhalt des Dreiecks.

Skizze nicht maßstäblich
2 BE
10
Wahlaufgabe Gleichungen und Funktionen
10.1
Ordne den Aussagen 1 und 2 jeweils die entsprechende Funktion zu.
- Der Graph der Funktion ist im gesamten Definitionsbereich steigend.
- Die Funktion hat keine Nullstelle.
|
A
|
mit |
|
|---|---|---|
|
B
|
mit |
|
|
C
|
mit |
2 BE
10.2
Wenn das Quadrat einer Zahl um 30 vermindert wird, ergibt sich das Siebenfache dieser Zahl.
Berechne die Zahlen, für die diese Aussage gilt.
2 BE
10.3
Eine Familie muss ihre Warmwasserbereitung erneuern. Bisher wird dazu ein elektrischer Warmwasserboiler genutzt. Es kann entweder nur der Boiler ersetzt oder auf Solarkollektoren mit Zusatzheizung umgestellt werden. Dazu werden folgende Angaben zusammengestellt:
Nach wie vielen Jahren werden sich die Gesamtkosten für den neuen Warmwasserboiler und die Solarkollektoren mit Zusatzheizung voraussichtlich auszugleichen?
| Anschaffungs- kosten |
Energie- kosten pro Jahr |
|
|---|---|---|
| neuer Warmwasserboiler | ||
| Solarkollektoren mit Zusatzheizung |
2 BE
10.4
Gegeben sind die Funktionen
 mit
mit  und
und
 mit
mit  und
und 
 ist
ist  Der Schnittpunkt der Graphen von
Der Schnittpunkt der Graphen von  und
und  im I. Quadranten ist
im I. Quadranten ist 
Der Graph einer linearen Funktion verläuft durch die Punkte
verläuft durch die Punkte  und
und  .
.
a)
Stelle die Funktionen  und
und  in ein und demselben Koordinatensystem grafisch dar.
in ein und demselben Koordinatensystem grafisch dar.
Der Scheitelpunkt von
2 BE
Der Graph einer linearen Funktion
b)
Überprüfe rechnerisch, ob  die Nullstelle der Funktion
die Nullstelle der Funktion  ist.
ist.
2 BE
10.5
Bei einem Parabelflug kann man in einem Flugzeug für 25 Sekunden Schwerelosigkeit erleben.
Ein Pilot berichtet:
„In 8,7 km Höhe nehme ich den Schub aus den Triebwerken und es beginnt der Parabelflug. Ab diesem Moment ist im Flugzeug alles schwerelos. Die maximale Höhe unseres Fluges beträgt 10,2 km. Nach 5,0 km in horizontaler Richtung haben wir unsere Ausgangshöhe wieder erreicht. Ich fange das Flugzeug ab und die Schwerkraft setzt wieder ein.“
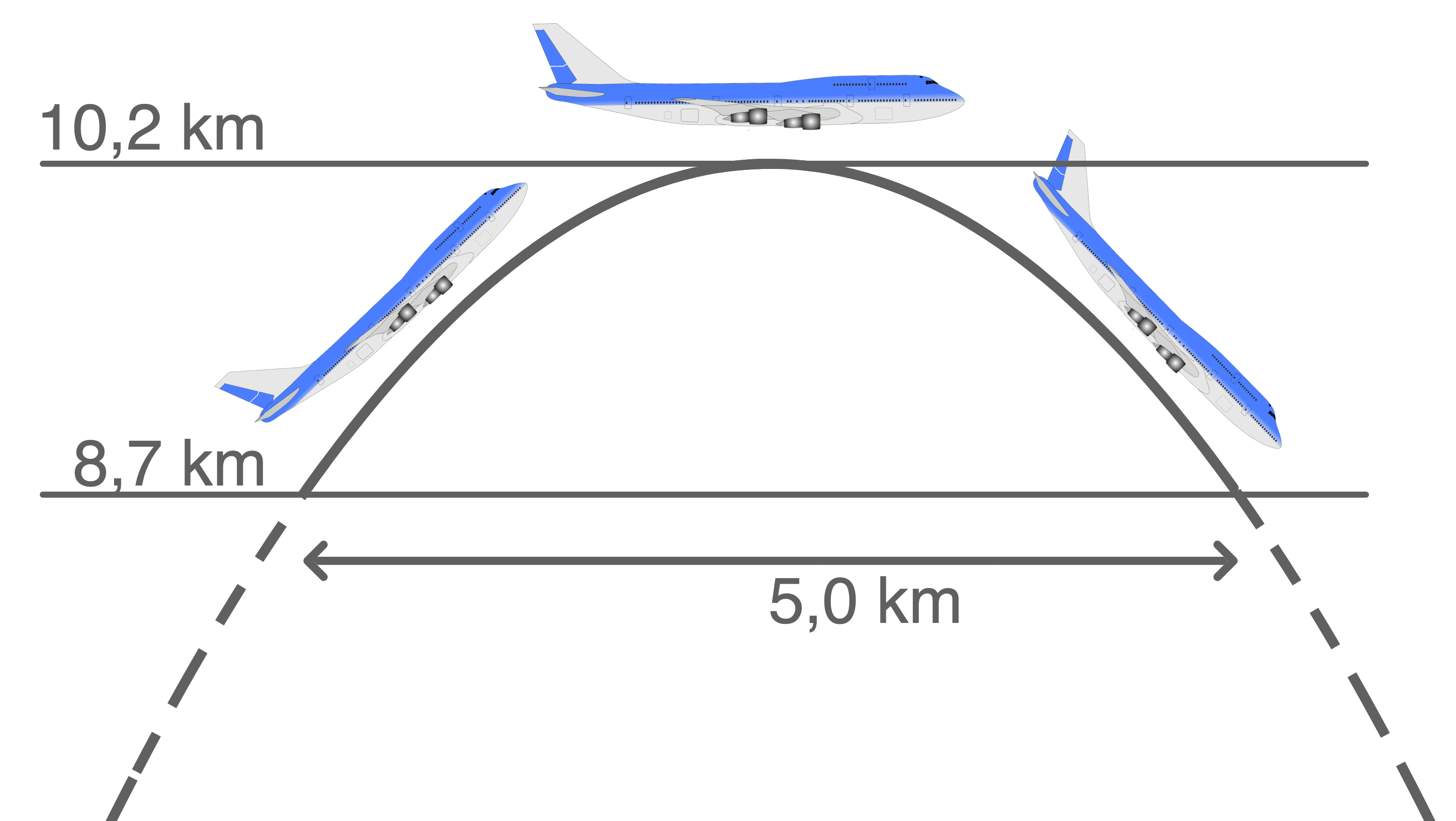
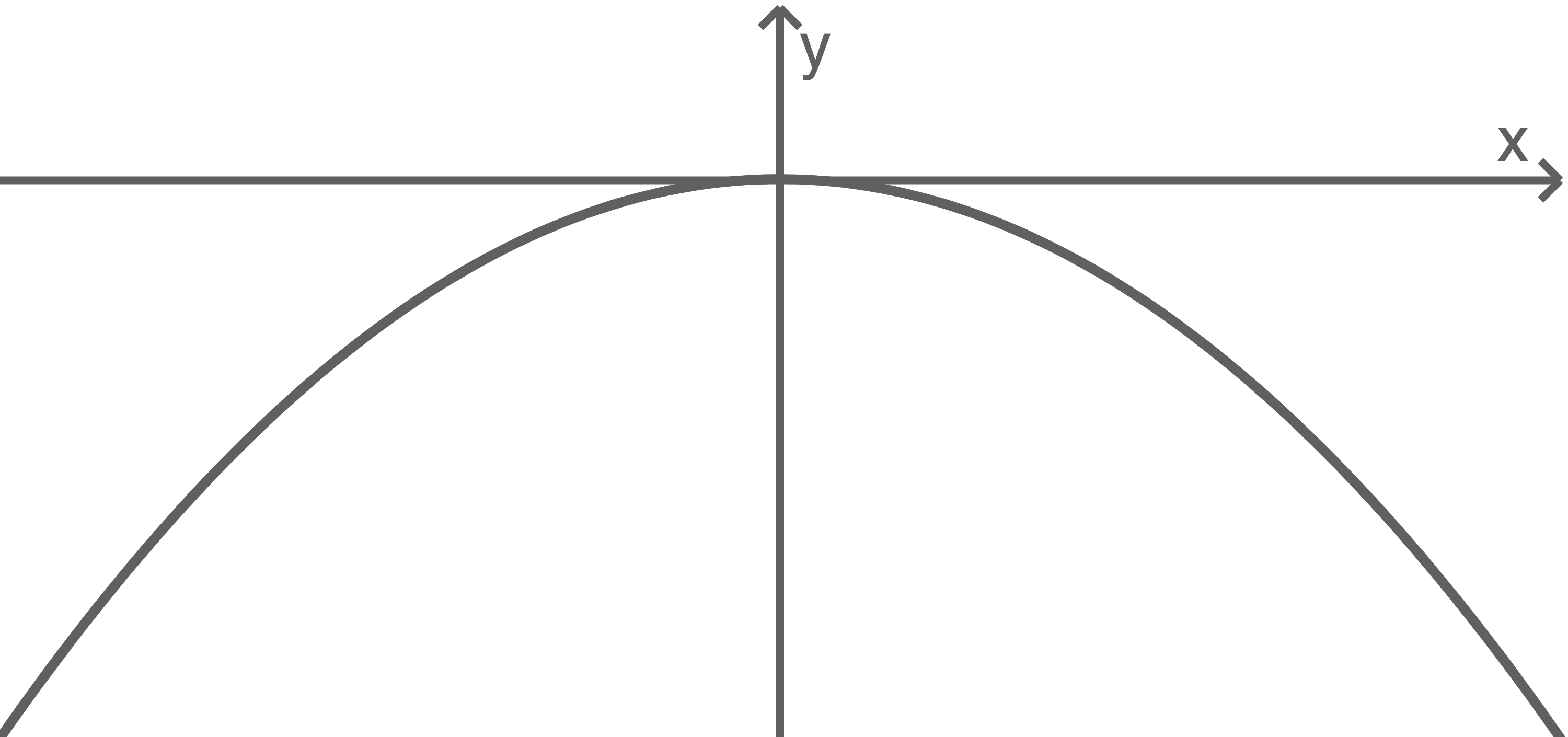 Die Flugbahn kann durch eine Funktion mit der Gleichung
Die Flugbahn kann durch eine Funktion mit der Gleichung  beschrieben werden.
Berechne den Faktor
beschrieben werden.
Berechne den Faktor  .
.
„In 8,7 km Höhe nehme ich den Schub aus den Triebwerken und es beginnt der Parabelflug. Ab diesem Moment ist im Flugzeug alles schwerelos. Die maximale Höhe unseres Fluges beträgt 10,2 km. Nach 5,0 km in horizontaler Richtung haben wir unsere Ausgangshöhe wieder erreicht. Ich fange das Flugzeug ab und die Schwerkraft setzt wieder ein.“

Skizze nicht maßstäblich

2 BE
9.1
Die 1. Aussage ist falsch.
Ein Rechteck hat im Allgemeinen nur zwei Symmetrieachsen, an der es gespiegelt werden kann, sodass das ursprüngliche Rechteck erhalten bleibt. Die 2. Aussage ist falsch.
Sind im Rechteck nicht alle Seiten gleich lang, so werden die Innenwinkel nicht mittig geteilt. Die 3. Aussage ist wahr.
Da die gegenüberliegenden Seiten eines Rechtecks immer gleich lang sind, folgt mit dem Satz des Pythagoras, dass die Diagonalen im Rechteck gleich lang sein müssen. Die 4. Aussage ist wahr.
Da jedes Quadrat auch die Eigenschaften eines Rechtecks erfüllt, ist ein Quadrat auch ein Rechteck mit vier gleich langen Seiten. Die Aussagen 3 und 4 sind richtig.
Ein Rechteck hat im Allgemeinen nur zwei Symmetrieachsen, an der es gespiegelt werden kann, sodass das ursprüngliche Rechteck erhalten bleibt. Die 2. Aussage ist falsch.
Sind im Rechteck nicht alle Seiten gleich lang, so werden die Innenwinkel nicht mittig geteilt. Die 3. Aussage ist wahr.
Da die gegenüberliegenden Seiten eines Rechtecks immer gleich lang sind, folgt mit dem Satz des Pythagoras, dass die Diagonalen im Rechteck gleich lang sein müssen. Die 4. Aussage ist wahr.
Da jedes Quadrat auch die Eigenschaften eines Rechtecks erfüllt, ist ein Quadrat auch ein Rechteck mit vier gleich langen Seiten. Die Aussagen 3 und 4 sind richtig.
9.2
Länge Schulweg Alex




![\(\begin{array}{rcl}
10\,\text{min} & \mathrel{\widehat{=}}& 3\,\text{km}\\[5pt]
1\,\text{min}& \mathrel{\widehat{=}}& 0,3\,\text{km}\\[5pt]
15\,\text{min} & \mathrel{\widehat{=}}& 4,5\,\text{km}
\end{array}\)](https://www.schullv.de/resources/formulas/dcd220eb488cc4757e673877915ca40bb9d9620f4909e705321c23b85017202d_light.svg)



 Alex Schulweg ist 4,5 km lang.
Länge Schulweg Benno
Alex Schulweg ist 4,5 km lang.
Länge Schulweg Benno




![\(\begin{array}{rcl}
60\,\text{min} & \mathrel{\widehat{=}}& 40\,\text{km}\\[5pt]
1\,\text{min}& \mathrel{\widehat{=}}& \dfrac{2}{3}\,\text{km}\\[5pt]
15\,\text{min} & \mathrel{\widehat{=}}& 10\,\text{km}
\end{array}\)](https://www.schullv.de/resources/formulas/8660c64d617dc50f0eef66eab39ecca90f4631ab27b10d3e84b020d2e9f3d3aa_light.svg)



 Bennos Schulweg ist 10 km lang.
Kosinussatz anwenden
Bennos Schulweg ist 10 km lang.
Kosinussatz anwenden
Mit dem Kosinussatz kann nun der Abstand zwischen den Wohnorten von Alex und Benno ermittelt werden.
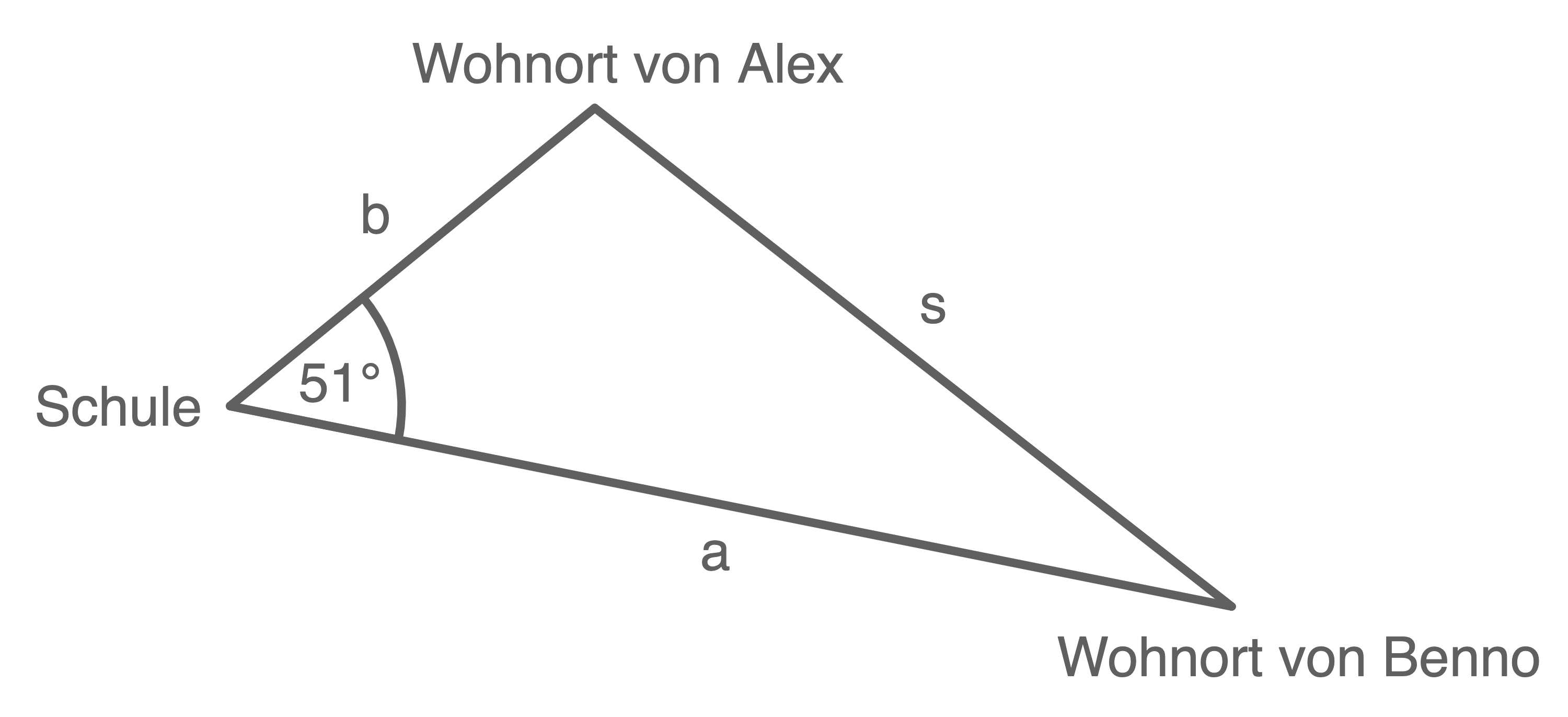
Die Straße zwischen den Wohnorten ist etwa 8 km lang.

9.3
a)
Der Flächeninhalt der neu zu befplanzenden Fläche kann berechnet werden, indem der Flächeninhalt der Fläche, die nicht neu bepflanzt werden soll, vom Flächeninhalt des gesamten Waldstücks abgezogen wird.
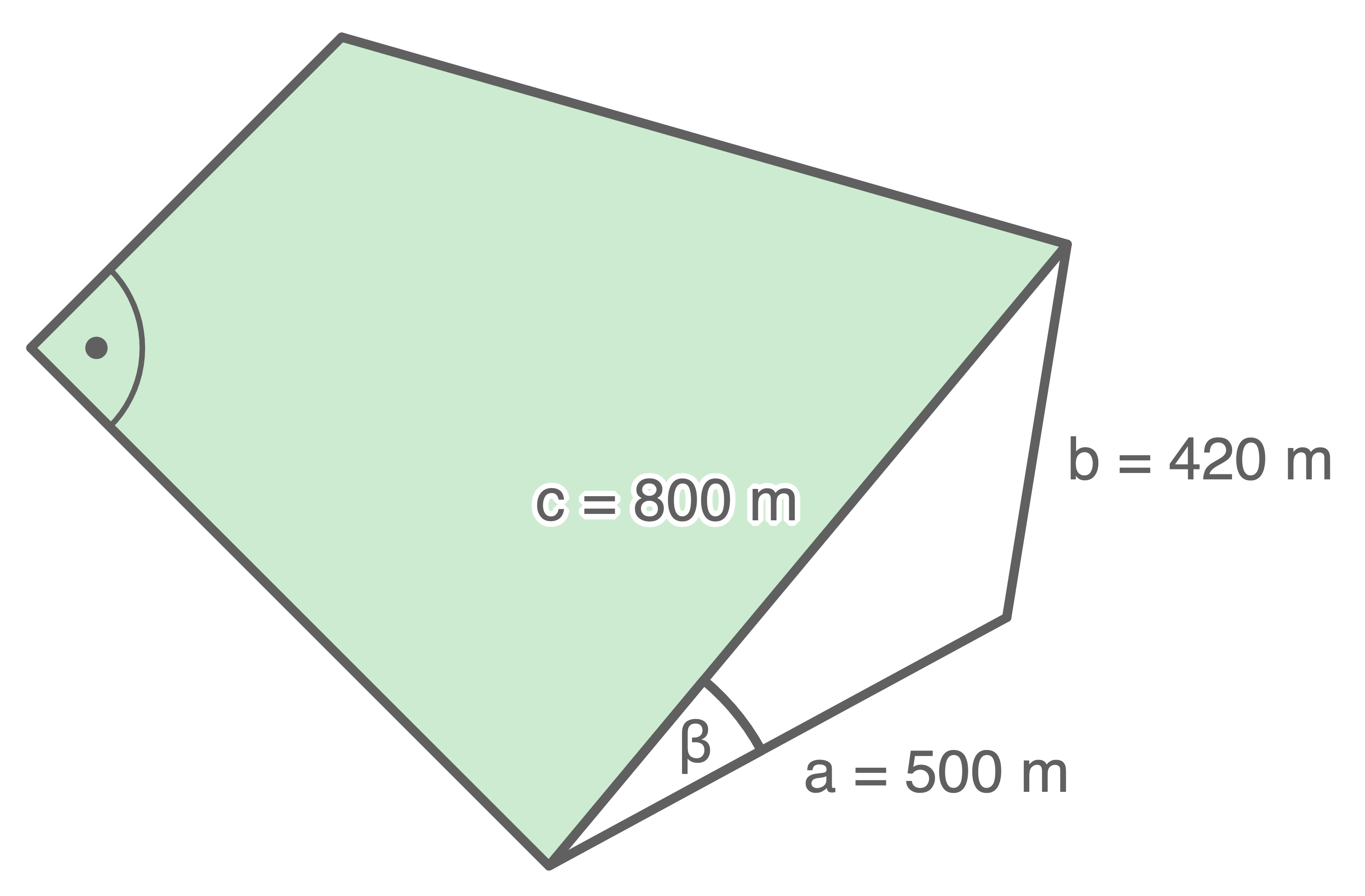 Dazu wird zunächst der Winkel
Dazu wird zunächst der Winkel  mit dem Kosinussatz berechnet:
Damit kann der Flächeninhalt des Dreiecks berechnet werden:
mit dem Kosinussatz berechnet:
Damit kann der Flächeninhalt des Dreiecks berechnet werden:
![\(\begin{array}[t]{rll}
A_D&=& \dfrac{1}{2}\cdot c\cdot a\cdot \sin\beta \\[5pt]
&\approx& \dfrac{1}{2}\cdot 800\,\text{m}\cdot 500\,\text{m} \cdot \sin 26,87° \\[5pt]
&\approx& 90\,394 \,\text{m}^2 \\[5pt]
&\approx& 9\,\text{ha}
\end{array}\)](https://www.schullv.de/resources/formulas/fdac91ae53306c769dc0ef93d515229c727b296d16e6258261b653e241843921_light.svg) Der Flächeninhalt der neu zu beflanzenden Fläche beträgt damit:
Der Flächeninhalt der neu zu beflanzenden Fläche beträgt damit:


b)
Es bietet sich an, den Maßstab  zu wählen. Dadurch ergeben sich die folgenden Längen:
zu wählen. Dadurch ergeben sich die folgenden Längen:
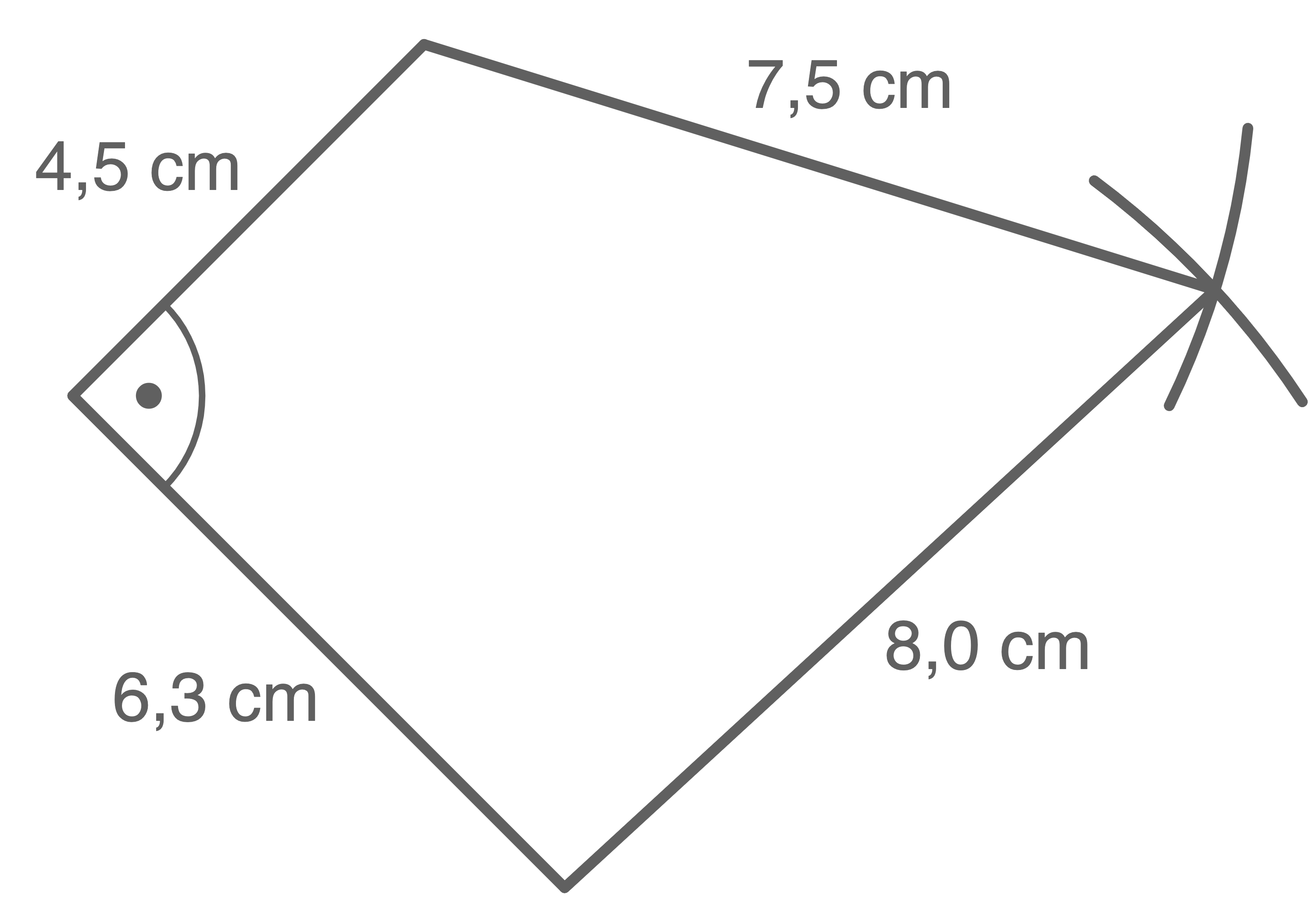 Je nach Bildschirmgröße kann die Messung variieren. Die Vorgehensweise bleibt jedoch die gleiche.
Je nach Bildschirmgröße kann die Messung variieren. Die Vorgehensweise bleibt jedoch die gleiche.

9.4
Das Dreieck und das Trapez besitzen die gleiche Höhe  sowie die Grundfläche
sowie die Grundfläche  Mit der Formel für den Flächeninhalt eines Dreiecks gilt:
Mit der Formel für den Flächeninhalt eines Dreiecks gilt:
 Für den Flächeninhalt eines Trapezes gilt:
Für den Flächeninhalt eines Trapezes gilt:
![\(\begin{array}[t]{rll}
A_T&=& \dfrac{a+2a}{2}\cdot h \\[5pt]
&=& \dfrac{3a}{2}\cdot h \\[5pt]
&=& 3\cdot \dfrac{a\cdot h}{2} \\[5pt]
&=&3\cdot A_{\Delta}
\end{array}\)](https://www.schullv.de/resources/formulas/a43241e36f8bf4ce6938a371b902bb70285ec11536efd366cb253764d70e4074_light.svg) Damit ist gezeigt, dass der Flächeninhalt des Trapezes dreimal so groß wie der Flächeninhalt des Dreiecks ist.
Damit ist gezeigt, dass der Flächeninhalt des Trapezes dreimal so groß wie der Flächeninhalt des Dreiecks ist.
10.1
Aussage 1 zuordnen
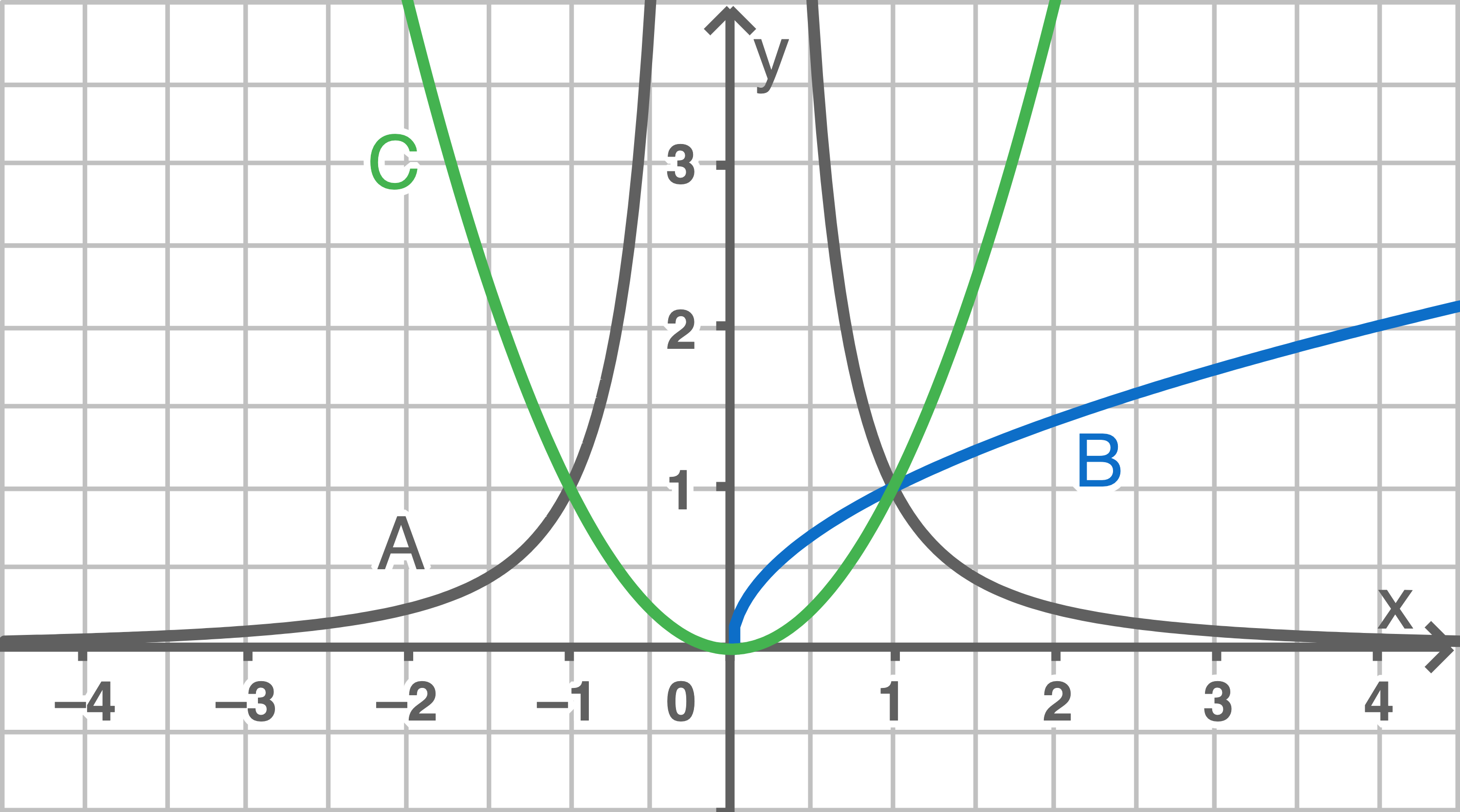 Es lässt sich erkennen, dass nur der Graph B im gesamten Definitionsbereich steigende Werte besitzt. Damit gehört Aussage 1 zu B.
Aussage 2 zuordnen
Die Graphen der Fuktionen B und C haben jeweils eine Nullstelle an der Stelle
Es lässt sich erkennen, dass nur der Graph B im gesamten Definitionsbereich steigende Werte besitzt. Damit gehört Aussage 1 zu B.
Aussage 2 zuordnen
Die Graphen der Fuktionen B und C haben jeweils eine Nullstelle an der Stelle  Der Graph der Funktion A hat dagegen keine Nullstelle.
Damit gehört A zur Aussage 2.
Der Graph der Funktion A hat dagegen keine Nullstelle.
Damit gehört A zur Aussage 2.

Skizze
10.2
Die Aussage führt auf die folgende Gleichung:
 Umstellen dieser Gleichung liefert:
Umstellen dieser Gleichung liefert:
 Es gilt also
Es gilt also  und
und  Die Nullstellen können nun mit der Lösungsformel berechnet werden.
Die Nullstellen können nun mit der Lösungsformel berechnet werden.
![\(\begin{array}[t]{rll}
x_{1/2}&=& -\dfrac{p}{2} \pm \sqrt{\left( \dfrac{p}{2}\right)^2 - q} \\[5pt]
&=& -\dfrac{-7}{2} \pm \sqrt{\left( -\dfrac{7}{2}\right)^2 - (-30)}\\[5pt]
&=&\dfrac{7}{2} \pm \sqrt{ \dfrac{169}{4}}\\[5pt]
&=&\dfrac{7}{2} \pm \dfrac{13}{2}\\[5pt]
x_{1}&=&\dfrac{7}{2} + \dfrac{13}{2}=\dfrac{20}{2}=10\\[5pt]
x_{2}&=&\dfrac{7}{2} - \dfrac{13}{2}=-\dfrac{6}{2}=-3\\
\end{array}\)](https://www.schullv.de/resources/formulas/1ab8fd84caafaf0bb068293fc401523509fcae0cec9fb592a06b96cc5d75d154_light.svg) Die Aussage gilt für die Zahlen -3 und 10.
Die Aussage gilt für die Zahlen -3 und 10.
10.3
Für die beiden Warmwasserbereitungen wird jeweils eine Gleichung aufgestellt. Dabei beschreibt  die Gesamtkosten und
die Gesamtkosten und  die Anzahl der Jahre.
Kostengleichung für den neuen Warmwasserboiler:
die Anzahl der Jahre.
Kostengleichung für den neuen Warmwasserboiler:
 Kostengleichung für die Solarkollektoren mit Zusatzheizung:
Kostengleichung für die Solarkollektoren mit Zusatzheizung:
 Gleichsetzen der beiden Gleichungen liefert die Anzahl der Jahre, nach denen die Kosten gleich sind:
Nach 7 Jahren haben sich die Kosten ausgeglichen.
Gleichsetzen der beiden Gleichungen liefert die Anzahl der Jahre, nach denen die Kosten gleich sind:
Nach 7 Jahren haben sich die Kosten ausgeglichen.
10.4
a)
Die Funktion  ist eine verschobene Normalparabel. Um diese grafisch darzustellen, wird der Scheitelpunkt berechnet.
ist eine verschobene Normalparabel. Um diese grafisch darzustellen, wird der Scheitelpunkt berechnet.
 Es gilt
Es gilt  und
und 


 Für die Funktion
Für die Funktion  wird eine Wertetabelle angelegt.
wird eine Wertetabelle angelegt.
Damit können nun die beiden Funktionen grafisch dargestellt werden.
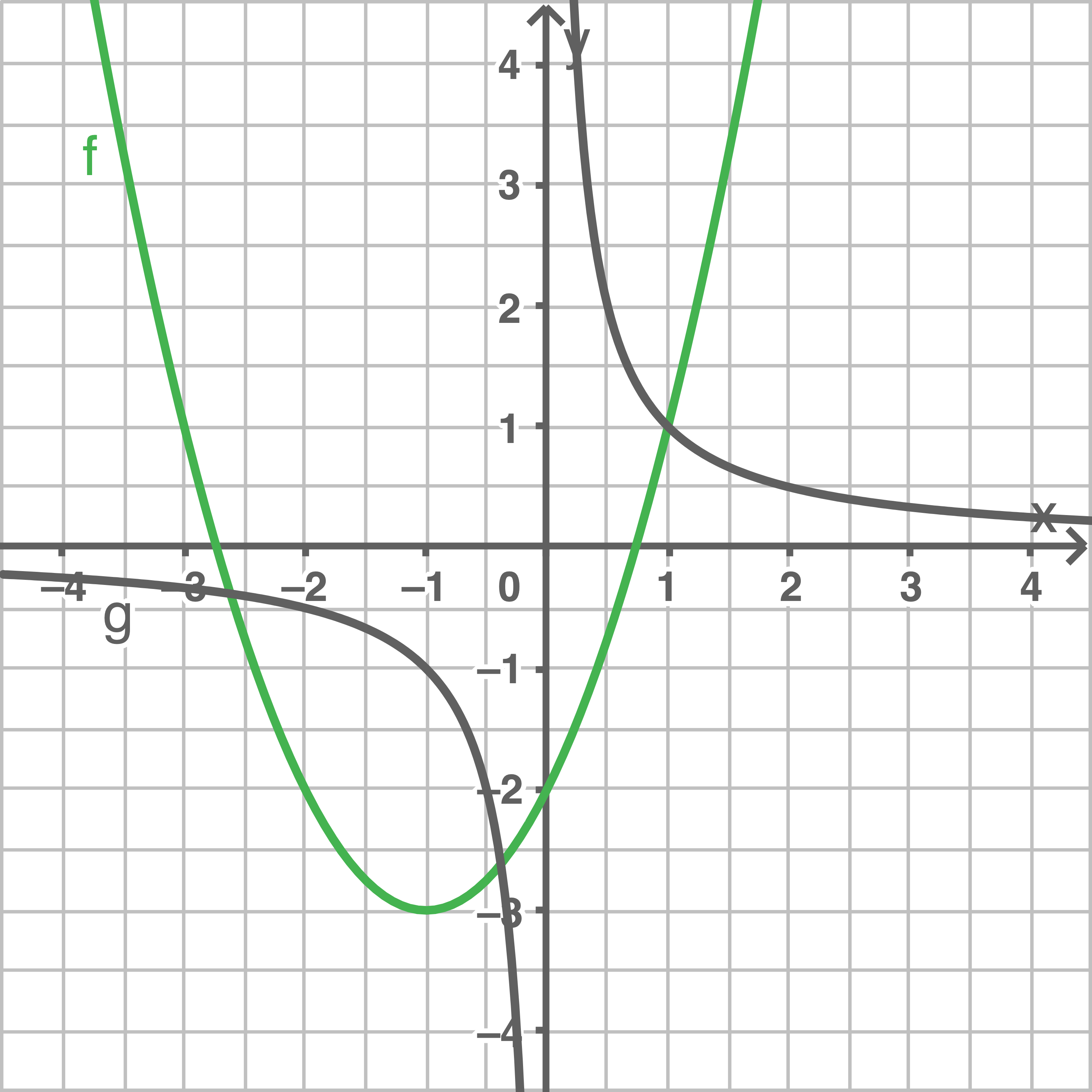

b)
Zunächst muss die Funktionsgleichung der Funktion  aufgestellt werden.
aufgestellt werden.
 Die Geradengleichung hat also die Form
Die Geradengleichung hat also die Form  Einsetzen der Koordinaten von
Einsetzen der Koordinaten von  liefert:
liefert:
![\(\begin{array}[t]{rll}
-3&=& 2\cdot (-1)+n \quad \scriptsize \mid\; +2\\[5pt]
-1&=& n
\end{array}\)](https://www.schullv.de/resources/formulas/986a606ea2dd25d14909c92fe69b04c0e584791462d41abc7bee0e7f6a1467be_light.svg) Damit ergibt sich die Geradengleichung
Damit ergibt sich die Geradengleichung  Nun muss noch überprüft werden, ob 0,5 eine Nullstelle der Funktion
Nun muss noch überprüft werden, ob 0,5 eine Nullstelle der Funktion  ist. Einsetzen ergibt:
ist. Einsetzen ergibt:
![\(\begin{array}[t]{rll}
y&=& 0,5\cdot 2-1 \\[5pt]
&=& 1-1 \\[5pt]
&=& 0
\end{array}\)](https://www.schullv.de/resources/formulas/b8c83160570297d42f5ca9281899048dcb4939f9c6d972b01fc884822f697496_light.svg) Folglich ist 0,5 eine Nullstelle der Funktion
Folglich ist 0,5 eine Nullstelle der Funktion 
Grafisches Aufstellen der Geradengleichung
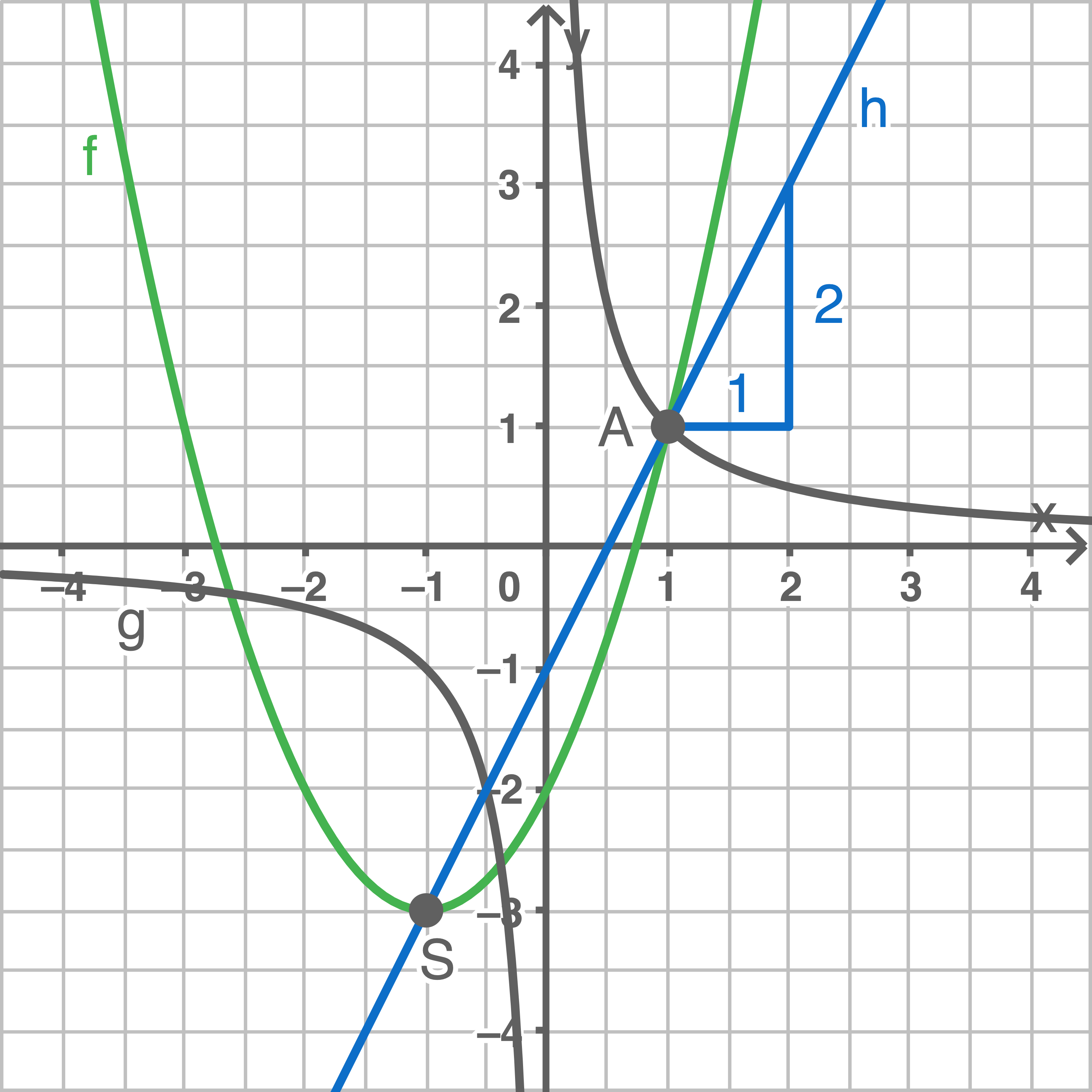 Aus der Skizze lassen sich die folgenden Werte ablesen:
Steigung:
Aus der Skizze lassen sich die folgenden Werte ablesen:
Steigung: 
 -Achsenabschnitt:
-Achsenabschnitt:  Damit ergibt sich die Geradengleichung:
Damit ergibt sich die Geradengleichung:

Rechnerisches Aufstellen der Geradengleichung

10.5
Um den Faktor  zu bestimmen wird ein Punkt auf der Parabel bestimmt und in die Parabelgleichung eingesetzt.
zu bestimmen wird ein Punkt auf der Parabel bestimmt und in die Parabelgleichung eingesetzt.
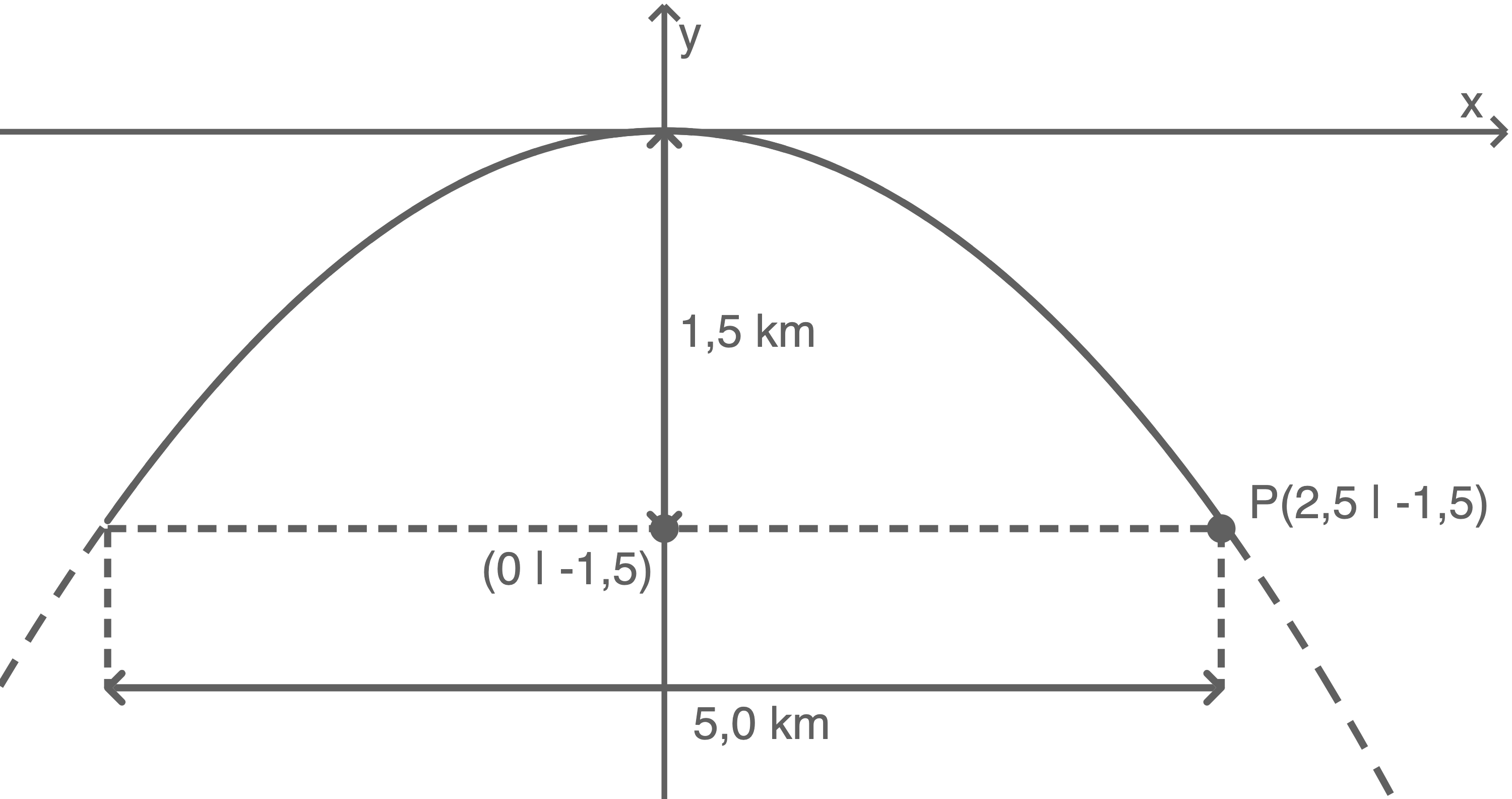 In der Skizze lässt sich erkennen, dass die Parabel den Punkt
In der Skizze lässt sich erkennen, dass die Parabel den Punkt  durchläuft. Einsetzen der Koordinaten des Punktes
durchläuft. Einsetzen der Koordinaten des Punktes  in die Gleichung liefert:
in die Gleichung liefert:
![\(\begin{array}[t]{rll}
-1,5&=&a \cdot (2,5)^2\\[5pt]
-1,5&=&a \cdot 6,25 \mid \; \scriptsize :6,25\\[5pt]
-0,24&=&a&\\
\end{array}\)](https://www.schullv.de/resources/formulas/247531e45219fcff6b5f1314a00fc402656ee502e39b40eec4c73f6737616142_light.svg) Es gilt
Es gilt  und die Parabelgleichung lautet:
und die Parabelgleichung lautet:  .
.

Skizze