Wahlaufgaben
9
Wahlaufgabe Stochastik
9.1
Max füllt seinen Bonbonspender mit 10 blauen, 13 roten, 9 weißen und 8 grünen Bonbons.
a)
Gib die Wahrscheinlichkeit dafür an, dass Max nach einmaligem Betätigen des Spenders ein blaues Bonbon erhält.
Max betätigt den Spender zweimal. Erst dann öffnet er die Ausgabeklappe.
1 BE
b)
Berechne die Wahrscheinlichkeit dafür, dass er ein grünes und ein weißes Bonbon findet.
2 BE
9.2
Bei einem Glücksrad werden die Zahlen „1“, „2“ und „3“ mit folgenden Wahrscheinlichkeiten angezeigt.
Zeichne ein solches Glücksrad.
| Zahl | |||
|---|---|---|---|
| Wahrscheinlichkeit |
2 BE
9.3
Der Lehrer zeigt ein Zufallsexperiment mit folgenden Eigenschaften:
- Das Experiment ist einstufig.
- Die Wahrscheinlichkeit eines Ereignisses beträgt
1 BE
10
Wahlaufgabe Geometrie
Lena und Paul erben Grundstücke. Jeder Quadratmeter dieser Grundstücke ist  wert. Lena bekommt das größere Grundstück. Um das Erbe gerecht aufzuteilen, muss sie an Paul Geld zahlen.
wert. Lena bekommt das größere Grundstück. Um das Erbe gerecht aufzuteilen, muss sie an Paul Geld zahlen.
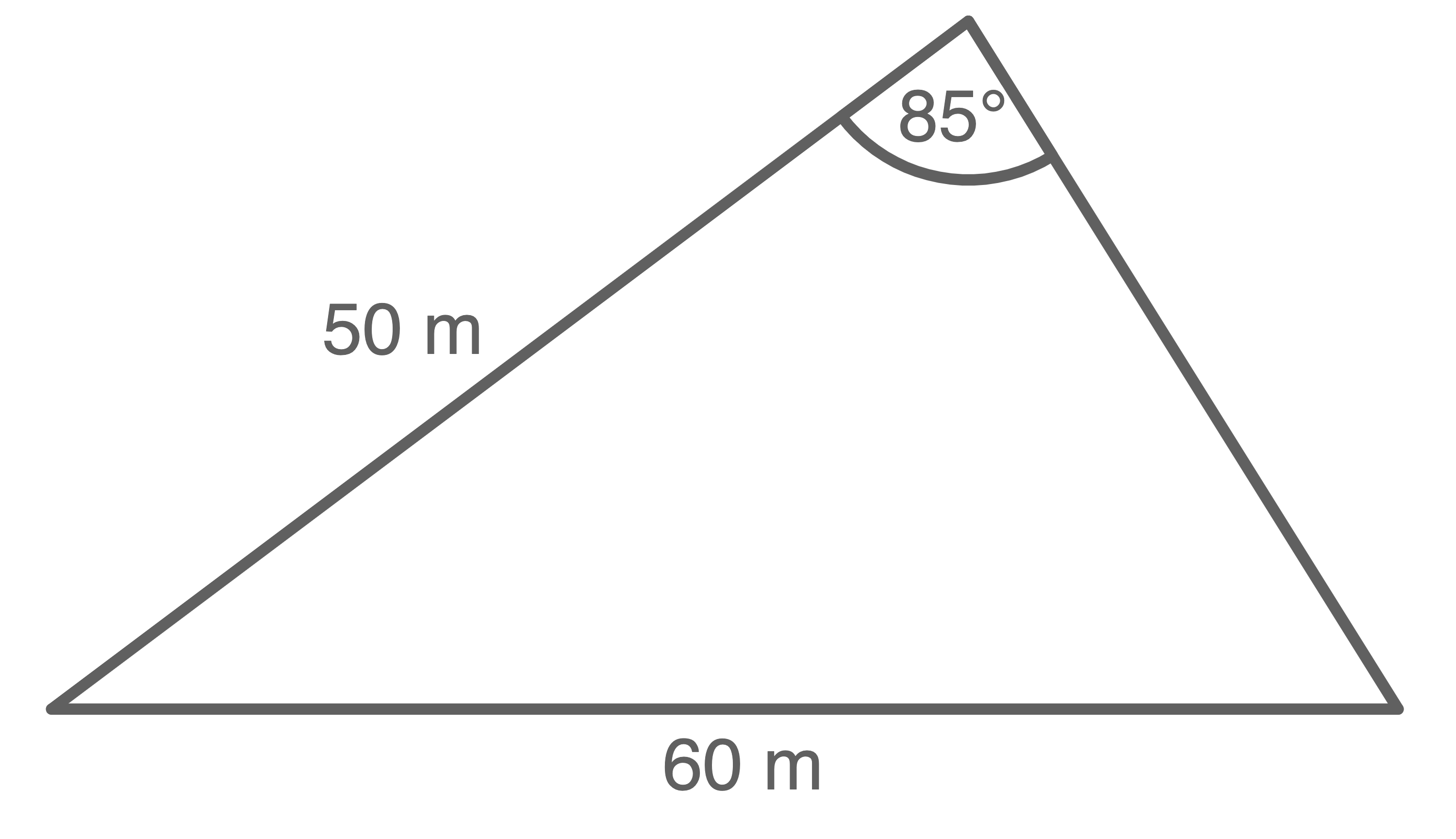
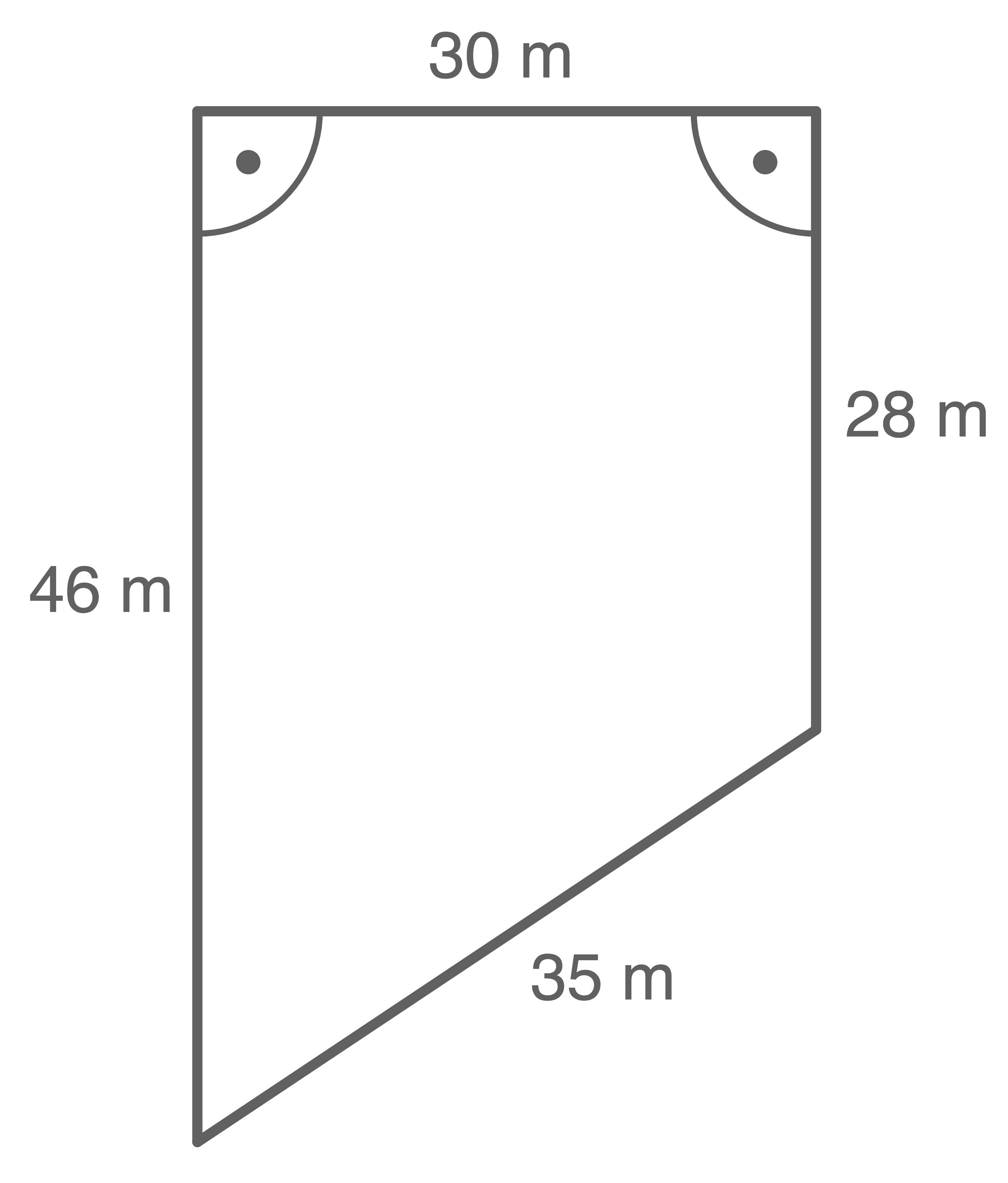

Skizzen nicht maßstäblich

a)
Berechne den Geldbetrag, den Lena an Paul zahlen muss.
4 BE
b)
Zeichne das dreieckige Grundstück in einem geeigneten Maßstab.
Gib diesen an.
Gib diesen an.
2 BE
11
Wahlaufgabe Funktionen
11.1
Die Graphen zweier Funktionen  und
und  schneiden sich im Punkt
schneiden sich im Punkt  Beide Funktionen haben eine gemeinsame Nullstelle bei
Beide Funktionen haben eine gemeinsame Nullstelle bei 
a)
Stelle zwei solche Funktionen im Koordinatensystem  graphisch dar.
graphisch dar.
2 BE
b)
Berechne den Abstand der Schnittpunkte der Graphen der Funktionen  und
und 
1 BE
c)
Gib die Gleichung zu einer dieser Funktionen an.
1 BE
11.2
Kaffee wird in eine Thermoskanne gefüllt. Nach dem Einfüllen nimmt die Termperatur des Kaffees je 5 Minuten um  ab. Nach drei Stunden hat der Kaffee eine Temperatur von
ab. Nach drei Stunden hat der Kaffee eine Temperatur von  Berechne die Temperatur, die der Kaffee beim Einfüllen hatte.
Berechne die Temperatur, die der Kaffee beim Einfüllen hatte.
2 BE
12
Wahlaufgabe Arithmetik/Algebra
12.1
Robert möchte am Automaten Geld abheben. Seine vierstellige Geheimzahl (PIN) besteht nur aus vier verschiedenen Primzahlen.
 ab. Er erhält viermal so viele 5-Euro-Scheine wie 10-Euro-Scheine und halb so viele 20-Euro-Scheine wie 10-Euro-Scheine.
ab. Er erhält viermal so viele 5-Euro-Scheine wie 10-Euro-Scheine und halb so viele 20-Euro-Scheine wie 10-Euro-Scheine.
a)
Gib eine Möglichkeit für Roberts Geheimzahl an.
Robert hebt
1 BE
b)
Ermittle die Anzahl der ausgezahlten 5-Euro-, 10-Euro- und 20-Euro-Scheine.
2 BE
12.2
Berechne.

1 BE
12.3
Löse die Gleichung.

2 BE
9.1
a)
Anzahl aller Bonbons: 
Anzahl blauer Bonbons:
![\(\begin{array}[t]{rll}
&P(\text{blau}) \\[5pt]
=& \dfrac{\text{Anzahl blaue Bonbons}}{\text{Anzahl alle Bonbons}} \\[5pt]
=& \dfrac{10}{40} \\[5pt]
=& \dfrac{1}{4}
\end{array}\)](https://www.schullv.de/resources/formulas/dbe1d4f36fb4caeea14e096b2b66016ac8aa70254a411e45e2d8641ebbd3c5c6_light.svg) Mit einer Wahrscheinlichkeit von
Mit einer Wahrscheinlichkeit von  erhält Max nach einmaligem Betätigen des Spenders ein blaues Bonbon.
erhält Max nach einmaligem Betätigen des Spenders ein blaues Bonbon.
Anzahl blauer Bonbons:
b)
Es handelt sich um Ziehen ohne Zurücklegen und ein zweistufiges Zufallsexperiment. Die Reihenfolge, in der die Farben gezogen werden, ist jedoch egal. Mithilfe der Pfadregeln ergibt sich:
![\(\begin{array}[t]{rll}
& P(\text{grün und weiß}) \\[5pt]
=& P(\text{grün, weiß})+P(\text{weiß, grün})\\[5pt]
=& \dfrac{8}{40} \cdot \dfrac{9}{39}+\dfrac{9}{40} \cdot \dfrac{8}{39} \\[5pt]
=& \dfrac{6}{25}
\end{array}\)](https://www.schullv.de/resources/formulas/f36c3a5a1a3f53e6b109071b19bfef514478f73e8204461f91778479199dab7a_light.svg) Mit einer Wahrscheinlichkeit von
Mit einer Wahrscheinlichkeit von  findet Max ein grünes und ein weißes Bonbon.
findet Max ein grünes und ein weißes Bonbon.
9.2
Winkel 1:  Winkel 2:
Winkel 2:  Winkel 3:
Winkel 3: 
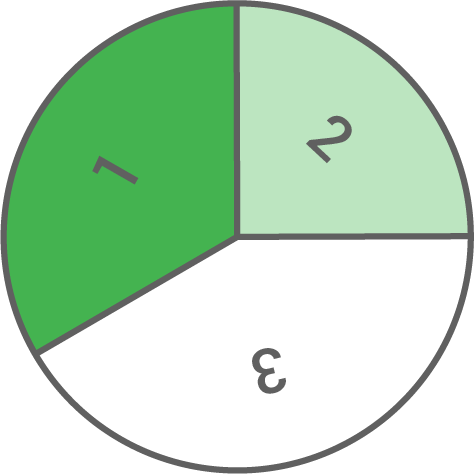
9.3
Ein mögliches Zufallsexperiment ist beispielsweise das Werfen eines fairen Würfels, der mit den Zahlen von  bis
bis  beschriftet ist.
Ein Ereignis mit der Wahrscheinlichkeit
beschriftet ist.
Ein Ereignis mit der Wahrscheinlichkeit  ist dann beispielsweise: „Es wird eine 6 gewürfelt.“
ist dann beispielsweise: „Es wird eine 6 gewürfelt.“
10
a)
Wert des dreieckigen Grundstücks berechnen
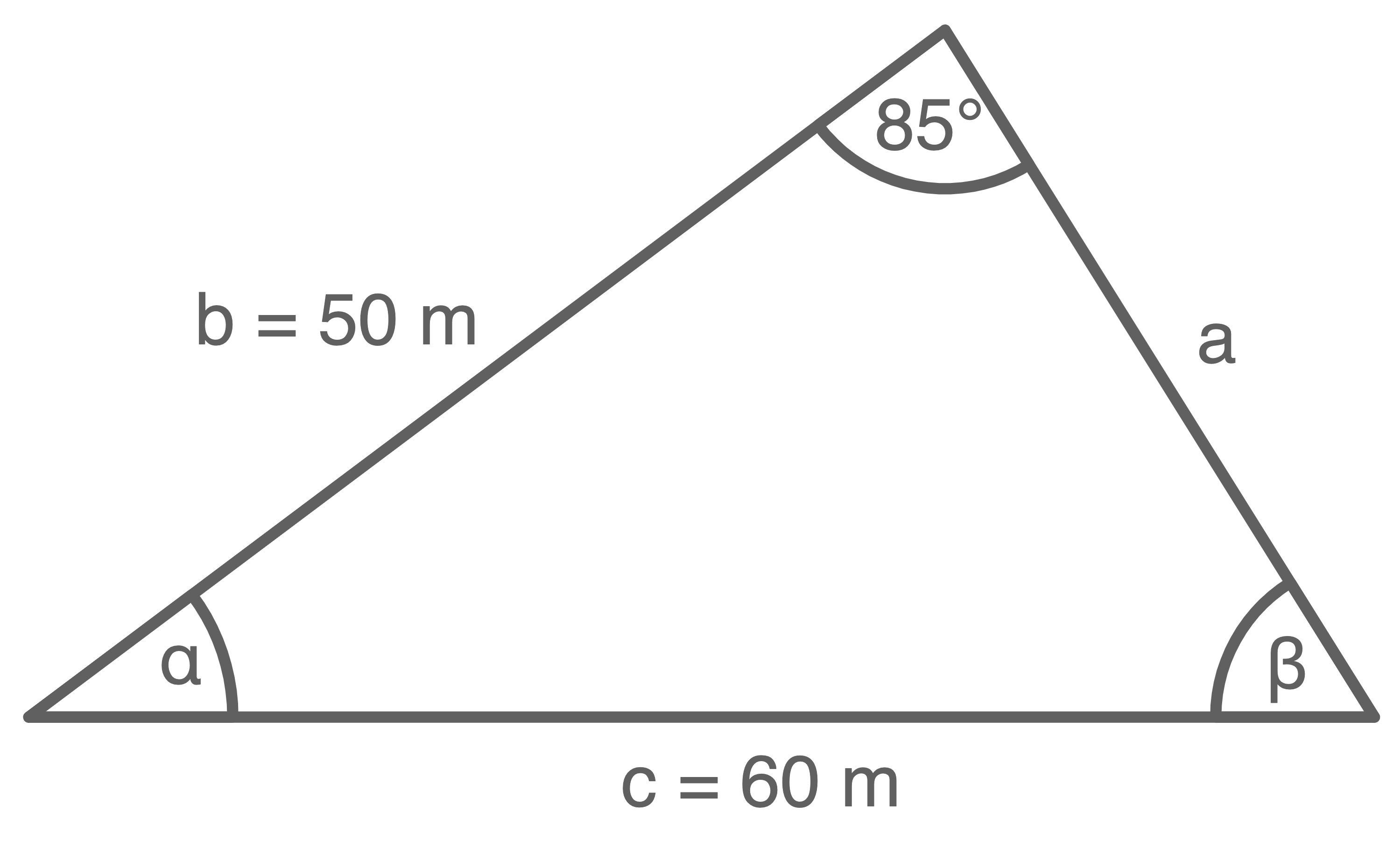
 berechnet werden:
berechnet werden:
![\(\begin{array}[t]{rll}
\alpha&=& 180^{\circ} -85^{\circ} - 56^{\circ} \\[5pt]
&=& 39^{\circ}
\end{array}\)](https://www.schullv.de/resources/formulas/ab239b8ab9a25f552de19bf4850ede3cc22c06c7aa2360dd2d8a2b02e1e46911_light.svg) Der Flächeninhalt des Grundstücks kann dann mithilfe der Formel für den Flächeninhalt eines Dreiecks berechnet werden:
Der Flächeninhalt des Grundstücks kann dann mithilfe der Formel für den Flächeninhalt eines Dreiecks berechnet werden:
![\(\begin{array}[t]{rll}
A_1&=& \dfrac{1}{2}\cdot b\cdot c \cdot \sin \alpha\\[5pt]
&=& \dfrac{1}{2}\cdot 50\,\text{m}\cdot 60\,\text{m} \cdot \sin 39^{\circ}\\[5pt]
&\approx& 944\,\text{m}^2 \\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/4a90fa4fbd7f63926ab81676e1e0a914db6cbcfa643c96df4fadb4dad3349bd9_light.svg) Der Wert des dreieckigen Grundstücks ist also:
Der Wert des dreieckigen Grundstücks ist also:
 Wert des viereckigen Grundstücks berechnen
Wert des viereckigen Grundstücks berechnen
 Lena muss die Häfte dieser Differenz an Paul zahlen, um das Erbe gerecht aufzuteilen.
Lena muss die Häfte dieser Differenz an Paul zahlen, um das Erbe gerecht aufzuteilen.
 Lena muss
Lena muss  an Paul zahlen.
an Paul zahlen.

Mit dem Sinussatz kann die Größe des Winkels  berechnet werden:
berechnet werden:
![\(\begin{array}[t]{rll}
\dfrac{c}{\sin \gamma} &=& \dfrac{b}{\sin \beta} \quad \scriptsize \mid\;\cdot \sin \beta\\[5pt]
\dfrac{c}{\sin \gamma}\cdot \sin \beta &=& b \quad \scriptsize \mid\; :\dfrac{c}{\sin \gamma} \\[5pt]
\sin \beta &=& b\cdot \dfrac{\sin \gamma}{c} \\[5pt]
\sin \beta&=& 50\,\text{m}\cdot \dfrac{\sin 85^{\circ}}{60\,\text{m}} \quad \scriptsize \mid\; \sin^{-1}\\[5pt]
\beta&\approx& 56° \\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/c890921c95357ad5c7a5241e5855314754da2dc0dc345be0da3ee52907b3e58a_light.svg)
Anhand der Winkelsumme eines Dreiecks kann nun die Größe des Winkels 
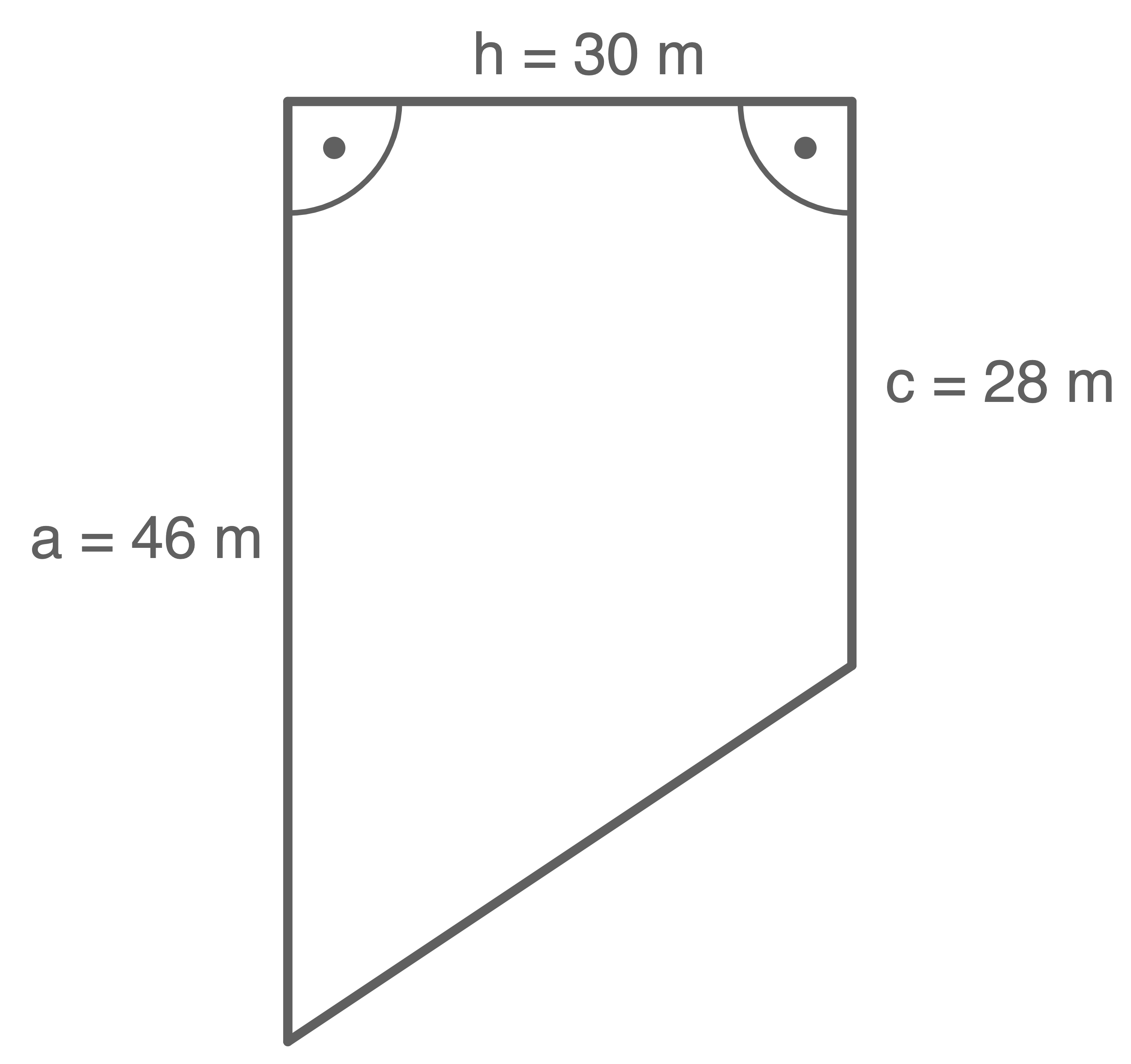
Das Grundstück hat die Form eines Trapezes. Der Flächeninhalt ergibt sich daher zu:
![\(\begin{array}[t]{rll}
A_2&=& \dfrac{a+c}{2}\cdot h\\[5pt]
&=& \dfrac{46\,\text{m}+28\,\text{m}}{2}\cdot 30\,\text{m}\\[5pt]
&=& 1\,110\,\text{m}^2 \\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/3860af6eee642a08aaea66d026fab1611c61618170143ac1ded9e942123feddc_light.svg) Der Wert des viereckigen Grundstücks ist also:
Der Wert des viereckigen Grundstücks ist also:

Zu zahlenden Betrag berechnen
Differenz der Beträge:
b)
Ein sinnvoller Maßstab ist beispielsweise  Dann gilt für die Seitenlängen:
Dann gilt für die Seitenlängen:

 Das Dreieck kann dann konsturiert werden, indem zunächst die 5 cm lange Strecke eingezeichnet und auf einer Seite der Winkel von 85° abgetragen wird. Auf der anderen Seite wird mit einem Zirkel die Länge von 6 cm abgetragen.
Das Dreieck kann dann konsturiert werden, indem zunächst die 5 cm lange Strecke eingezeichnet und auf einer Seite der Winkel von 85° abgetragen wird. Auf der anderen Seite wird mit einem Zirkel die Länge von 6 cm abgetragen.
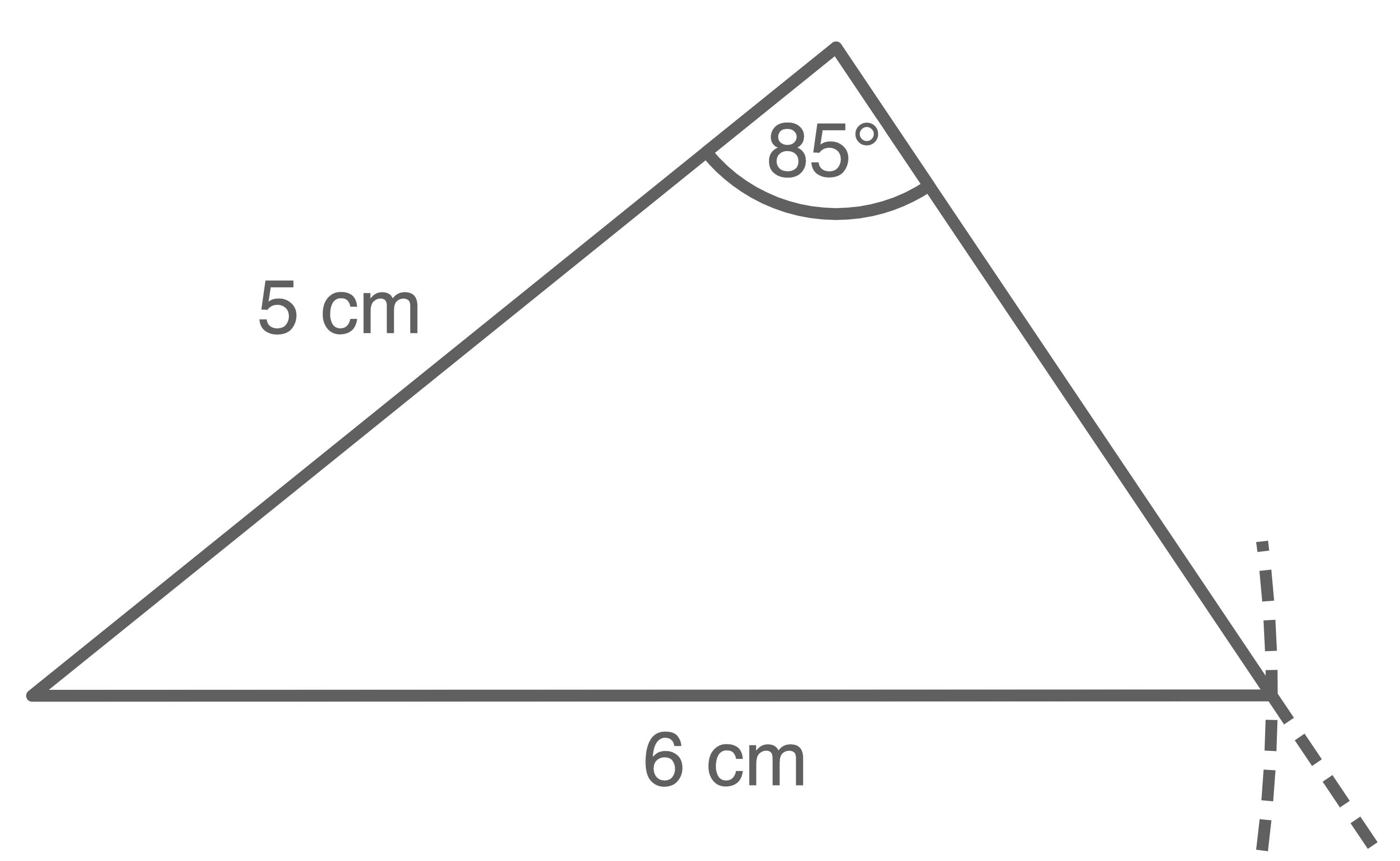 Je nach Bildschirmgröße kann die Messung variieren. Die Vorgehensweise bleibt jedoch die gleiche.
Je nach Bildschirmgröße kann die Messung variieren. Die Vorgehensweise bleibt jedoch die gleiche.

11.1
a)
Es gibt viele verschiedene Möglichkeiten. Eine ist beispielsweise die Folgende:
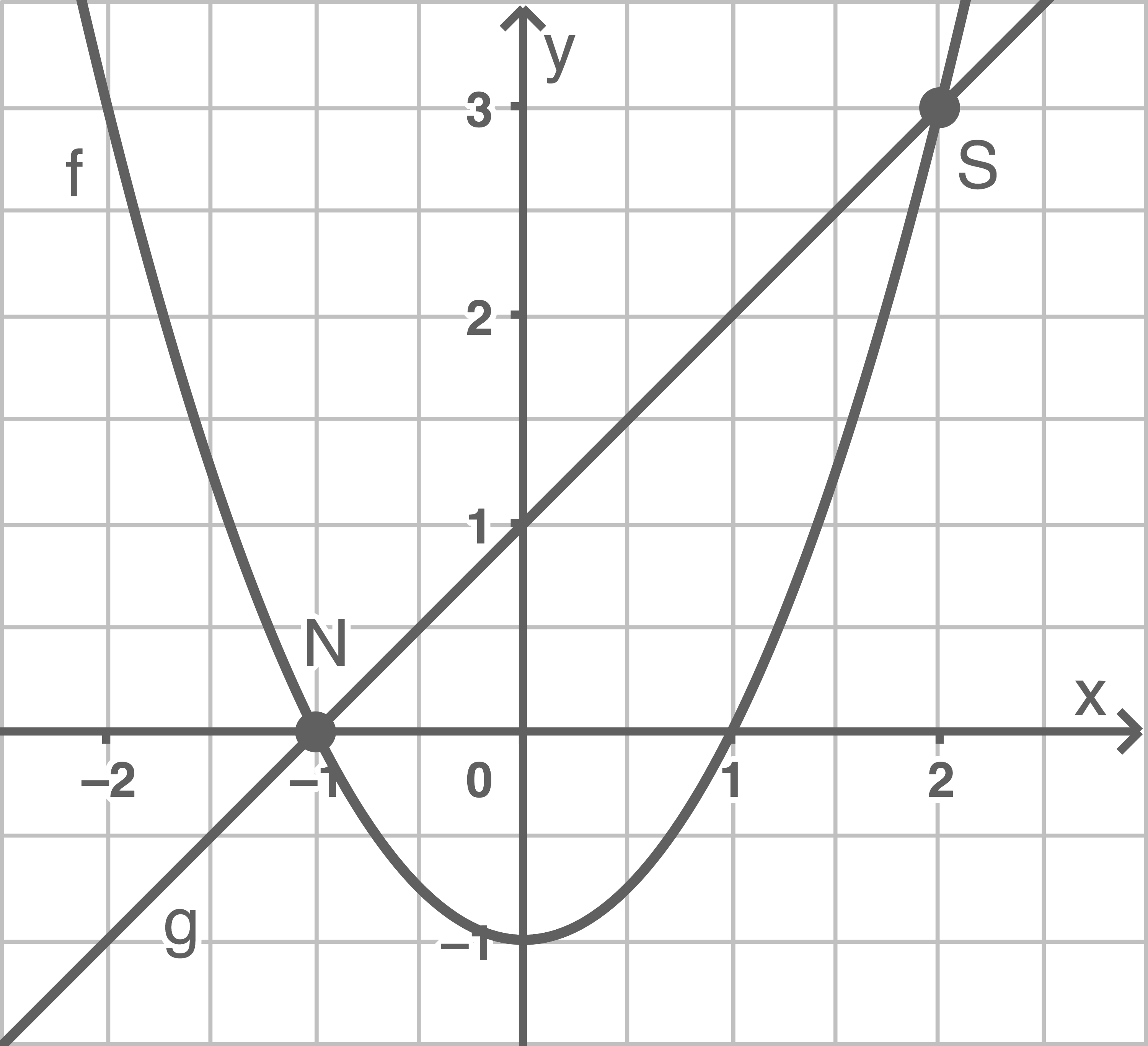

b)
Die Stecke  kann berechnet werden, indem wie in der Skizze ein Stützdreieck eingezeichnet wird, dessen Hypotenuse die Strecke
kann berechnet werden, indem wie in der Skizze ein Stützdreieck eingezeichnet wird, dessen Hypotenuse die Strecke  ist.
ist.
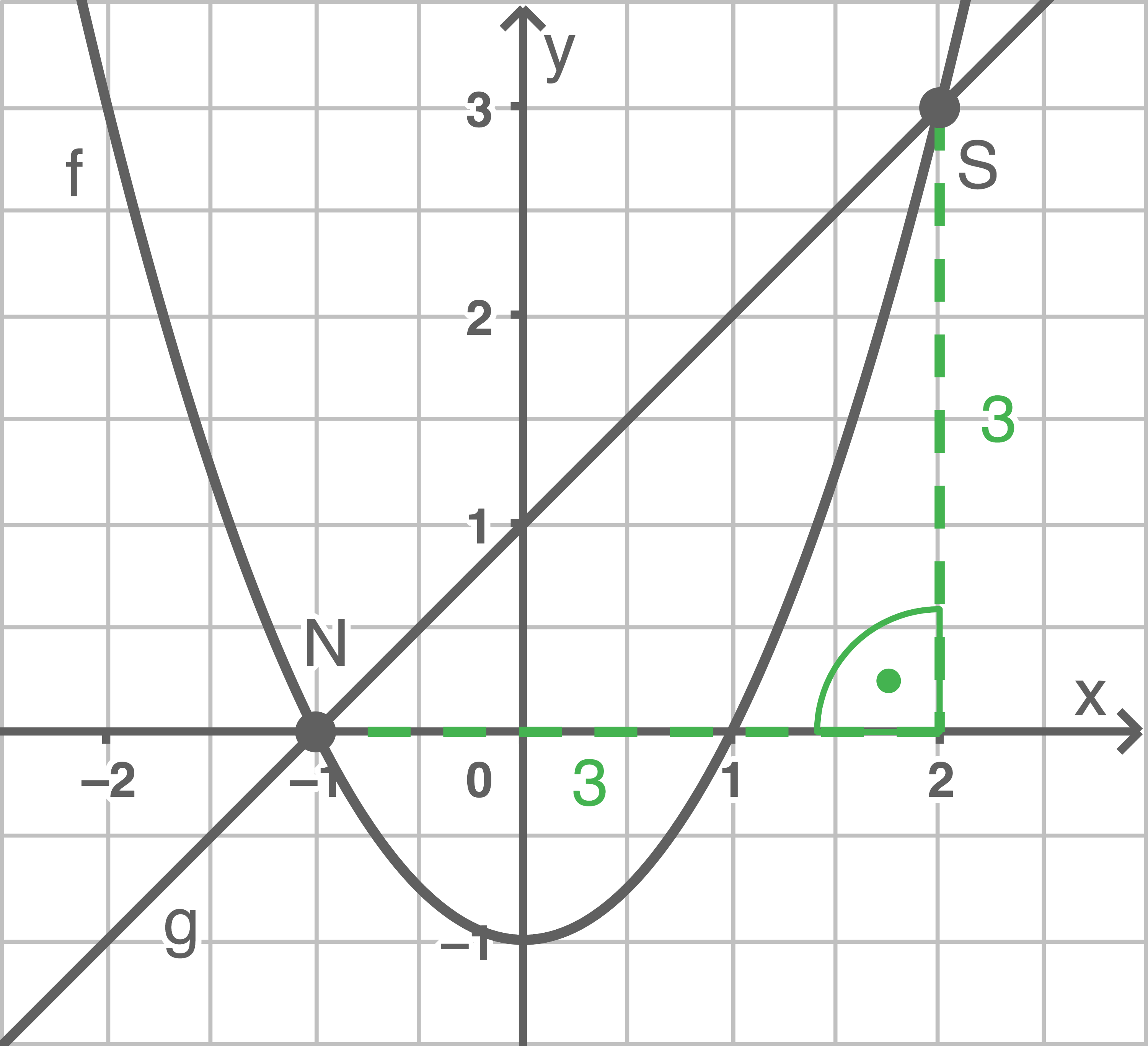 Die Längen der Strecken können der Abildung entnommen werden.
Mit dem Satz des Pythagoras folgt:
Die Längen der Strecken können der Abildung entnommen werden.
Mit dem Satz des Pythagoras folgt:
![\(\begin{array}[t]{rll}
\overline{SN}^2&=& (3\,\text{cm})^2 +(3\,\text{cm})^2 \\[5pt]
\overline{SN}^2&=& 18\,\text{cm}^2 \quad \scriptsize \mid\; \sqrt{\,} \\[5pt]
\overline{SN}&\approx& 4,24\,\text{cm}
\end{array}\)](https://www.schullv.de/resources/formulas/ef13b2770470d7abba2b20fb67be8fe771da0ccb9c1b7a29097d9854eaffe04a_light.svg)
Die beiden Schnittpunkte haben einen Abstand von ungefähr 
c)
Es gibt verschiedene Möglichkeiten. Hier wird beispielhaft die Gleichung der Funktion  aus Teilaufgabe a) bestimmt. Der Skizze kann entnommen werden, dass die Gerade durch die beiden Punkte die Steigung
aus Teilaufgabe a) bestimmt. Der Skizze kann entnommen werden, dass die Gerade durch die beiden Punkte die Steigung  hat. Zudem schneidet sie die
hat. Zudem schneidet sie die  -Achse an der Stelle
-Achse an der Stelle  der
der  -Achsenabschnitt beträgt also
-Achsenabschnitt beträgt also  Eine zugehörige Gleichung ist folglich:
Eine zugehörige Gleichung ist folglich:

11.2
Da die Temperatur um einen festen Prozentsatz abnimmt handelt es sich um einen exponentiellen Verfall mit einer Funktionsgleichung der Form  wobei
wobei  gilt.
gilt.

Abnahmerate: Da 3 Stunden
Da 3 Stunden  entsprechen, ergibt sich die folgende Gleichung:
entsprechen, ergibt sich die folgende Gleichung:
![\(\begin{array}[t]{rll}
G_n&=& G_0\cdot q^n \\[5pt]
60°C&=& G_0\cdot 0,99^{36} \quad \scriptsize \mid\; :0,99^{36}\\[5pt]
\dfrac{60°}{0,99^{36}}&=& G_0 \\[5pt]
86°C&\approx& G_0
\end{array}\)](https://www.schullv.de/resources/formulas/96182533036325556a18ade0320b08032251cc07e98d55ef0d91515127ea2722_light.svg) Der Kaffee hatte beim Einfüllen eine Temperatur von 86°C.
Der Kaffee hatte beim Einfüllen eine Temperatur von 86°C.
Abnahmerate:
12.1
a)
Roberts vierstellige Geheimzahl besteht aus vier verschiedenen Primzahlen, die aus nur einer Ziffer bestehen dürfen. Alle einstelligen Primzahlen sind:
 Eine mögliche Geheimzahl ist also
Eine mögliche Geheimzahl ist also 
b)
- Anzahl der 10-Euro-Scheine:
- Anzahl der 5-Euro-Scheine:
- Anzahl der 20-Euro-Scheine:
12.2
12.3
Umformen der Gleichung in Normalform:
![\(\begin{array}[t]{rll}
3x^2+2x&=&2x^2+3 &\quad \scriptsize \mid\; -2x^2 \\[5pt]
x^2 +2x&=& 3 &\quad \scriptsize \mid\; -3 \\[5pt]
x^2+2x-3&=& 0
\end{array}\)](https://www.schullv.de/resources/formulas/e91afa362c7f42df62ebbbf4a68a67d737f02094af5931e6060d7e39e6672d07_light.svg) Es gilt
Es gilt  und
und  Mit der Lösungsformel folgt:
Mit der Lösungsformel folgt:
![\(\begin{array}[t]{rll}
x_{1/2}&=& -\dfrac{2}{2}\pm \sqrt{\left(\dfrac{2}{2}\right)^2-(-3)} \\[5pt]
&=& -1\pm \sqrt{1+3} \\[5pt]
&=& -1\pm 2 \\[5pt]
x_1&=& -1-2 \\[5pt]
&=&-3 \\[10pt]
x_2&=& -1+2 \\[5pt]
&=& 1
\end{array}\)](https://www.schullv.de/resources/formulas/3956509daed4eaa4d86747e1fad682e214cbf4bdcb55c72a660c105780f50869_light.svg) Die Lösungen der Gleichung sind
Die Lösungen der Gleichung sind  und
und 