Wahlaufgaben

Wahlaufgabe Geometrie

9.1

Gegeben ist ein Viereck mit den angegebenen Eigenschaften.

Es hat zwei gleich lange Seitenpaare.
Die Diagonalen stehen senkrecht aufeinander.
Es gibt genau eine Symmetrieachse.

Gib die Art des Vierecks mit diesen Eigenschaften an.

1 BE

9.2

Eine Wandergruppe plant einen Wandertag vom Marktplatz aus in die nähere Umgebung. Die Strecke führt zum Ausflugslokal, über die Weggabelung und das Freibad zurück zum Marktplatz.
Die Wanderung ist von 08:00 Uhr bis 15:00 Uhr geplant. Die Wanderer gehen davon aus, in einer Stunde vier Kilometer Wegstrecke zu schaffen. Im Ausflugslokal wollen sie 45 min verweilen.

Skizze nicht maßstäblich

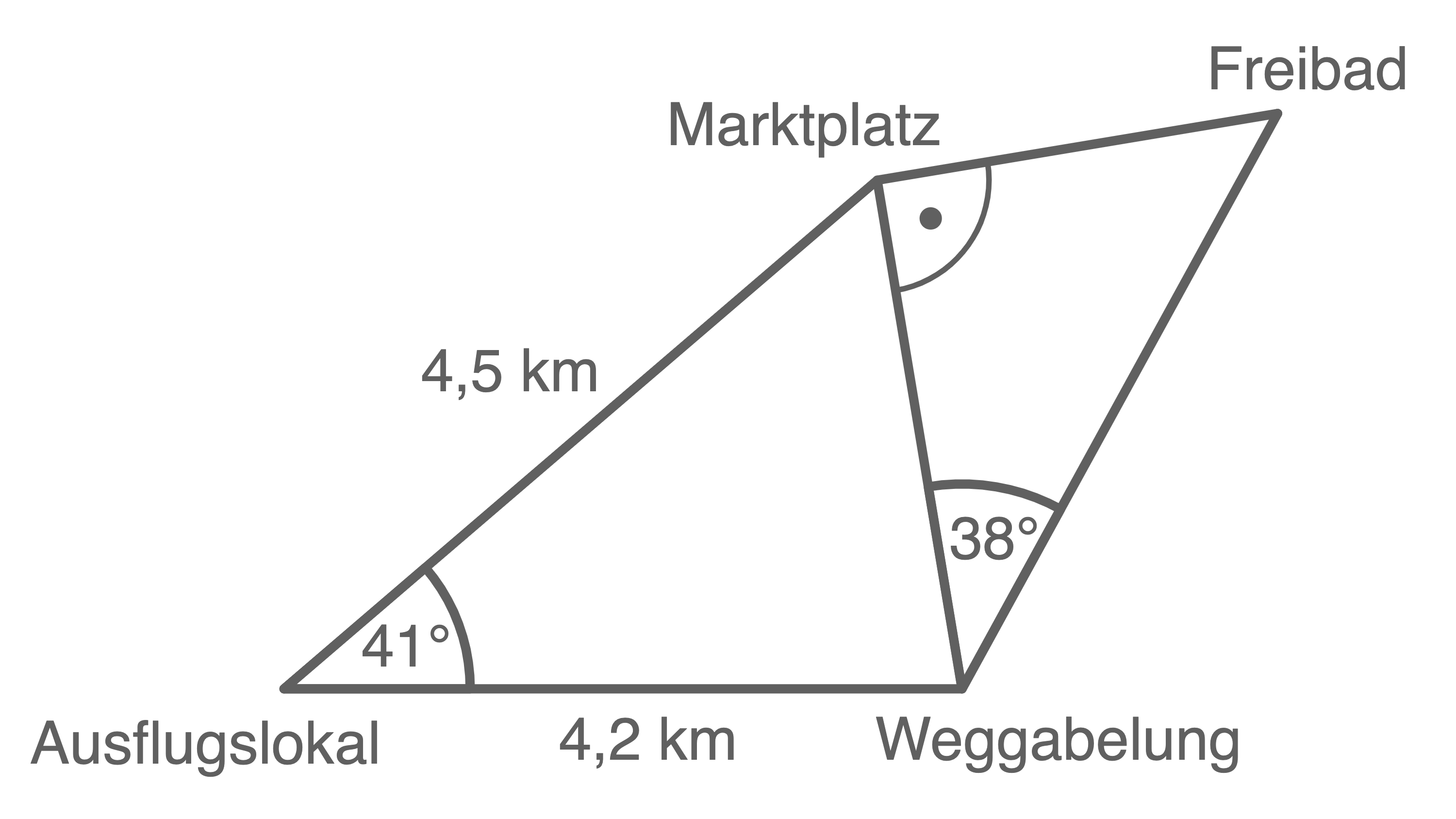Berechne die Zeit, die für den Aufenthalt im Freibad zur Verfügung steht.

5 BE

Wahlaufgabe Stochastik

10.1

In einem neuen Wohngebiet wurde eine Umfrage zur Anzahl der Kinder in den Familien durchgeführt. Die Ergebnisse sind in folgender Tabelle dargestellt.

Anzahl der Kinder	Anzahl der Familien
$0$	$11$
$1$	$19$
$2$	$23$
$3$	$9$
$4$	$3$

Berechne das arithmetische Mittel für die Anzahl der Kinder pro Familie.

1 BE

Durch den Zuzug weiterer fünf Familien verändert sich das arithmetische Mittel auf 1,7 Kinder pro Familie.

Die absoluten Häufigkeiten sollen so verändert werden, dass die Werte diesem Sachverhalt entsprechen.
Gib eine zugehörige Tabelle an.

2 BE

10.2

Ein Glücksrad ist in gleich große Felder aufgeteilt.
Ermittle die Wahrscheinlichkeit für das Ereignis:

„Beim Zweimaligen Drehen des Glücksrades ist die Summe der angezeigten Zahlen größer als 5.“

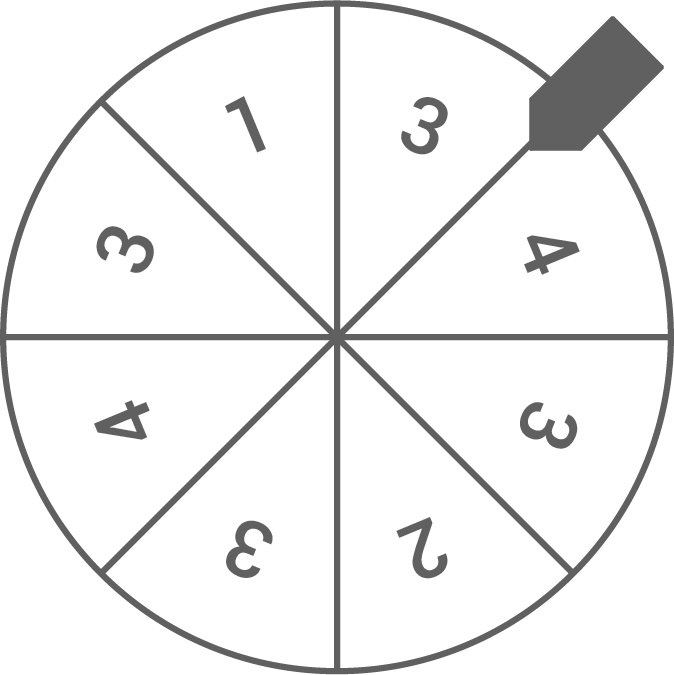
3 BE

Wahlaufgabe Funktionen

Ein Festzelt hat eine kreisförmige Grundfläche. Der Querschnitt ist parabelförmig. Die Funktion

$y=f(x)= -0,2x^2+7,2$ mit $x\in \mathbb{R}$

beschreibt diese Parabel, wobei eine Längeneinheit einem Meter entspricht.

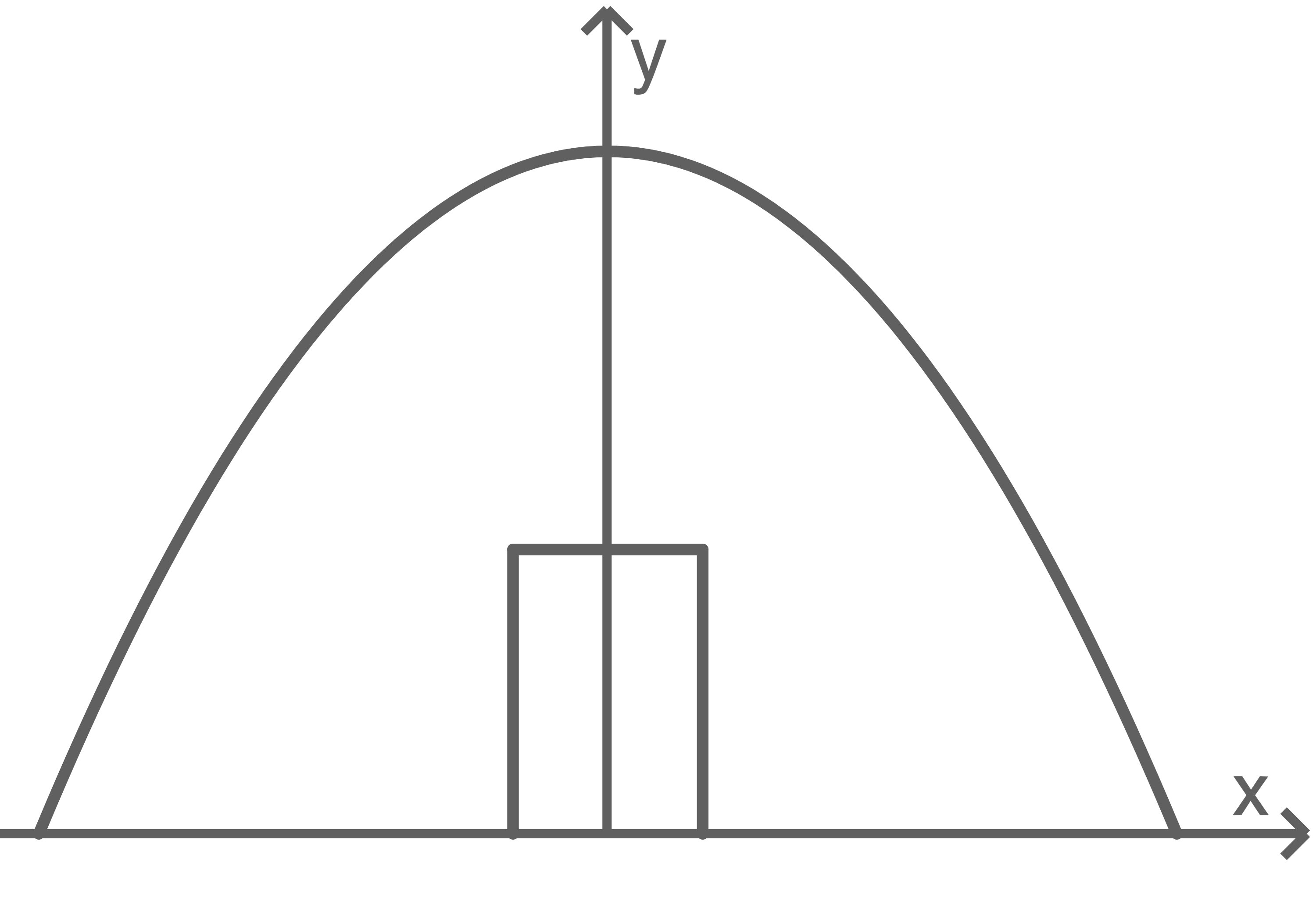
Skizze nicht maßstäblich

Gib die Höhe des Zeltes an.

1 BE

Berechne den Radius der Grundfläche des Zeltes.

1 BE

Bei Veranstaltungen in diesem Zelt kann nur der Teil der Grundfläche als Stehplatz genutzt werden, auf dem eine $1,80\,\text{m}$ große Person die Zeltwand nicht berührt.

Berechne den prozentualen Anteil der Grundfläche, der für Stehplätze genutzt werden kann.

4 BE

Wahlaufgabe Arithmetik/Algebra

12.1

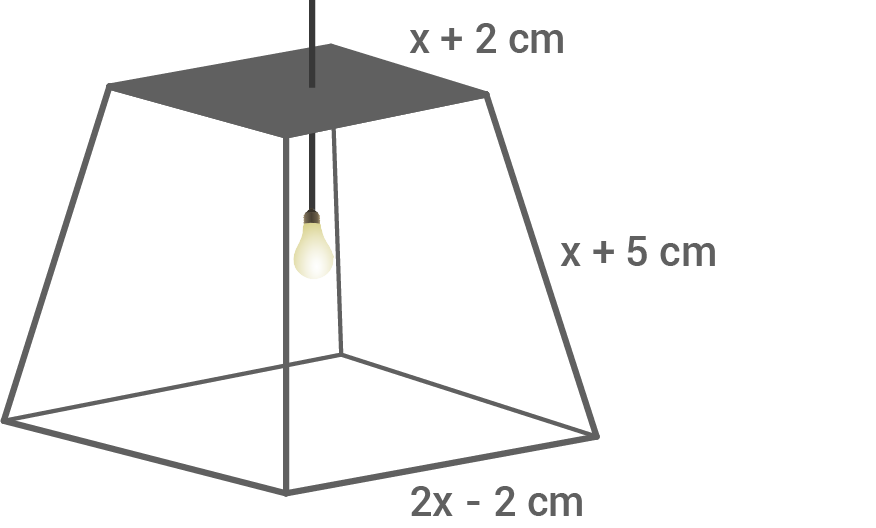
Die Glasplatten des Lampenschirms werden von Metallschienen zusammengehalten.
Grund- und Deckplatte sind Quadrate und die Seitenflächen sind gleichschenklige Trapeze.

Berechne die Gesamtlänge der benötigten Metallschienen für $x=18,5\,\text{cm}.$

2 BE

12.2

Löse die Gleichung .

$2x^2+12x+20 = x^2$

2 BE

12.3

Leas Vater ist dreimal so alt wie sie. Ihr Bruder ist 4 Jahre jünger als Lea. Zusammen sind die drei Personen 76 Jahre alt.

Berechne das Alter des Vaters und das Alter des Bruders.

2 BE

9.1

Für die erste Eigenschaft kommen Quadrate, Rechtecke, Rauten, Parallelogramme oder Drachenvierecke infrage.
Gilt zusätlich die zweite Eigenschaft, so bleiben nur Quadrate, Rauten und Drachenvierecke.
Von diesen erfüllt nur noch das Drachenviereck die dritte Eigenschaft.

Es handelt sich also um ein Drachenviereck.

9.2

Zunächst müssen noch die fehlenden Strecken berechnet werden. Es werden folgende Bezeichnungen verwendet:

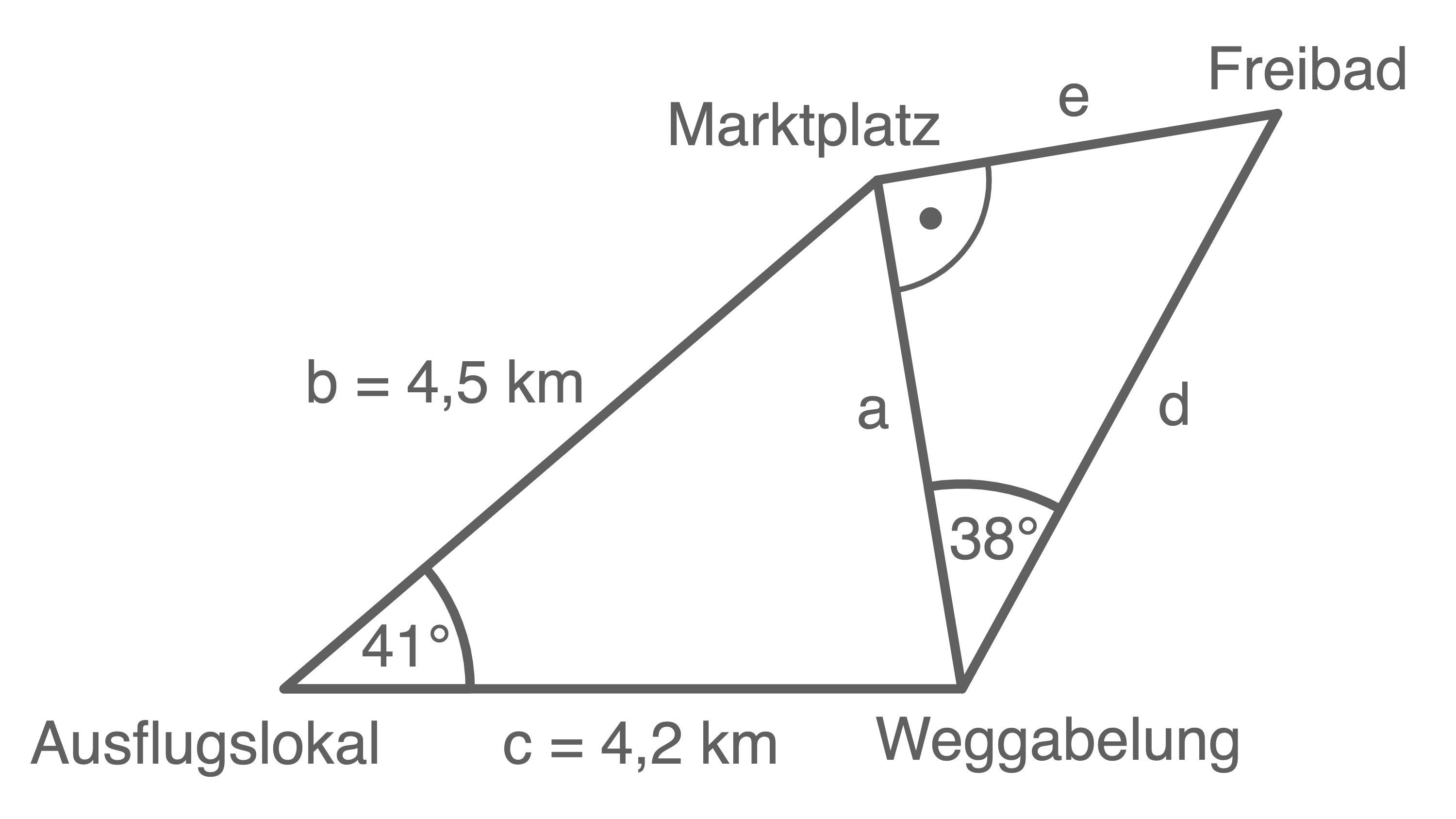Mit dem Kosinussatz folgt für die Länge der Strecke $a:$

Rechenweg anzeigen

$a\approx 3,1\,\text{km}$

Die Seite $d$ entspricht der Hypotenuse des rechtwinkligen Dreiecks. Die Länge dieser Seite lässt sich wie folgt berechnen:

$\begin{array}[t]{rll} \cos 38^{\circ} &=& \dfrac{\text{Ankathete}}{\text{Hypotenuse}} \\[5pt] \cos 38^{\circ} &=& \dfrac{a}{d} \quad \scriptsize \mid\;\cdot d \\[5pt] \cos 38^{\circ}\cdot d &=& a \quad \scriptsize \mid\;: \cos 38° \\[5pt] d&=& \dfrac{a}{\cos 38^{\circ}} \\[5pt] d&=& \dfrac{3,1\,\text{km}}{\cos 38^{\circ}} \\[5pt] d &\approx& 3,9\,\text{km} \end{array}$

Die Länge der Seite $e$ kann nun über den Satz des Pythagoras oder den Tangens berechnet werden:

Berechnung mit Tangens

$\begin{array}[t]{rll} \tan 38^{\circ} &=& \dfrac{\text{Gegenkathete}}{\text{Ankathete}} \\[5pt] \tan 38^{\circ} &=& \dfrac{e}{a}\quad \scriptsize \mid\; \cdot a\\[5pt] \tan 38^{\circ}\cdot a &=& e \\[5pt] \tan 38^{\circ}\cdot 3,1\,\text{km} &=& e \\[5pt] 2,4\,\text{km} &\approx& e \end{array}$

Berechnung mit dem Satz des Pythagoras

$\begin{array}[t]{rll} a^2+e^2&=& d^2 \quad \scriptsize \mid\; -a^2 \\[5pt] e^2&=& d^2-a^2 \\[5pt] e^2&=& (3,9\,\text{km})^2-(3,1\,\text{km})^2 \\[5pt] e^2&\approx& 5,6\,\text{km}^2 \quad \scriptsize \mid\; \sqrt{\,}\\[5pt] e&\approx& 2,4 \,\text{km} \end{array}$

Die Länge der gesamten Wanderstrecke beträgt damit:

$4,5\,\text{km} + 4,2\,\text{km} + 3,9\,\text{km} + 2,4\,\text{km} = 15\,\text{km}$

Die Wanderer legen im Schnitt pro Stunde vier Kilometer zurück. Damit kann die Zeit $t$ berechnet werden, die die Wanderer für die Wanderstrecke benötigen.

Rechnung mit der Verhältnisgleichung

$\begin{array}[t]{rll} \dfrac{1\,\text{h}}{4\,\text{km}}&=& \dfrac{t}{15\,\text{km}} \quad \scriptsize \mid\; \cdot 15\,\text{km} \\[5pt] \dfrac{1\,\text{h}}{4\,\text{km}} \cdot 15\,\text{km}&=& t \\[5pt] 3,75 \,\text{h}&=& t \end{array}$

Rechnung mit Dreisatz

$:4$

$\cdot 15$ Grau geschwungener Pfeil, der nach rechts unten zeigt.

$\begin{array}{rcl} 4 \,\text{km}& \mathrel{\widehat{=}}& 1\,\text{h}\\[5pt] 1 \,\text{km}& \mathrel{\widehat{=}}& 0,25\,\text{h}\\[5pt] 15 \,\text{km} & \mathrel{\widehat{=}}& 3,75\,\text{h} \end{array}$

$:4$

$\cdot 15$

Im Ausflugslokal wollen die Wanderer $45\,\text{min}=0,75\,\text{h}$ verweilen. Ohne Aufenthalt im Freibad benötigen sie also bereits $3,75\,\text{h}+0,75\,\text{h}=4,5\,\text{h}.$ Insgesamt stehen ihnen 7 Stunden zur Verfügung.

$7\,\text{h}-4,5\,\text{h}=2,5\,\text{h}$

Sie können also $2\,\text{h}$ und $30\,\text{min}$ im Freibad bleiben.

10.1

Rechenweg anzeigen

Anzahl Kinder: 104

Anzahl Familien: $11+19+23+9+3=65$

$\begin{array}[t]{rll} &\text{arithmetisches Mittel} \\[5pt] =& \dfrac{\text{Anzahl Kinder}}{\text{Anzahl Familien}} \\[5pt] =& \dfrac{104}{65}\\[5pt] =& 1,6 \end{array}$

Das arithmetische Mittel für die Anzahl der Kinder pro Familie beträgt $1,6.$

Neue Anzahl an Familien: $65+5=70$

Neue Anzahl $n$ an Kindern berechnen:

Rechenweg anzeigen

$n=119$

Zunahme der Anzahl an Kindern: $119-104=15$

Auf die 5 neuen Familien müssen also insgesamt 15 Kinder verteilt werden. Beispielsweise hat dann jede der Familien drei Kinder. Dann sieht die Tabelle wie folgt aus:

Anzahl der Kinder	$0$	$1$	$2$	$3$	$4$
Anzahl der Familien	$11$	$19$	$23$	$14$	$3$

10.2

$P(1)=\dfrac{\text { Anzahl der Felder mit einer 1}}{\text { Anzahl aller Felder }}=\dfrac{1}{8}$

Analog folgt:

$P(2)=\dfrac{1}{8}$

$P(3)=\dfrac{4}{8}=\dfrac{1}{2}$

$P(4)=\dfrac{2}{8}=\dfrac{1}{4}$

Mit den Pfadregeln folgt:

Rechenweg anzeigen

$P(\text{„Summe ist größer als 5“})=\dfrac{5}{8}$

Mit einer Wahrscheinlichkeit von $\dfrac{5}{8}=62,5\,\%$ ist die Summe der angezeigten Zahlen beim zweimaligen Drehen größer als 5.

Der Querschnitt des Zeltes ist achsensymmetrisch zur $y$ -Achse. Der höchste Punkt des Zeltes liegt daher auf der $y$ -Achse an der Stelle $x=0.$

$f(0)= -0,2\cdot 0^2 +7,2 = 7,2$

Das Zelt ist $7,2\,\text{m}$ hoch.

Der Radius der Grundfläche entspricht dem Abstand einer der beiden Nullstellen der Funktion $f(x)$ vom Ursprung.

Nullstellen berechnen:

$\begin{array}[t]{rll} f(x)&=& 0 \\[5pt] -0,2x^2+7,2&=& 0 \quad \scriptsize \mid\; -7,2\\[5pt] -0,2x^2&=& -7,2 \quad \scriptsize \mid\; :(-0,2)\\[5pt] x^2 &=& 36 \quad \scriptsize \mid\;\sqrt{\,} \\[5pt] x&=& \pm 6 \end{array}$

Die Parabel schneidet also bei $x_1=-6$ und $x_2=6$ die $x$ -Achse. Der Radius der Grundfläche beträgt daher $6\,\text{m}.$

Im Querschnitt wird die nutzbare Fläche links und rechts durch die Punkte begrenzt, an denen das Zelt eine Höhe von $1,80\,\text{m}$ besitzt. Dies sind die Punkte auf der Parabel, an denen $f(x)=1,80$ gilt.

$\begin{array}[t]{rll} f(x) &=& 1,80 \\[5pt] -0,2x^2+7,2&=& 1,80 \quad \scriptsize \mid\;-7,2 \\[5pt] -0,2x^2&=& -5,4 \quad \scriptsize \mid\; :(-0,2) \\[5pt] x^2 &=& 27 \quad \scriptsize \mid\; \sqrt{\,}\\[5pt] x &=& \pm\sqrt{27} \\[5pt] x_1&\approx& -5,2 \\[5pt] x_2&\approx& 5,2 \\[5pt] \end{array}$

Der Radius der nutzbaren Fläche ist also $r_n\approx 5,2\,\text{m}.$

Mit der Formel für den Flächeninhalt eines Kreises folgt für die Größe der nutzbaren Fläche:

$\begin{array}[t]{rll} A_n&=& \pi \cdot r_n^2 \\[5pt] &\approx& \pi\cdot (5,2\,\text{m})^2 \\[5pt] &\approx& 84,9\,\text{m}^2 \end{array}$

Nacht Teilaufgabe b) beträgt der Radius der Grundfläche $r_G = 6\,\text{m}.$ Für den Flächeninhalt der gesamten Grundfäche folgt:

$\begin{array}[t]{rll} A_G&=& \pi \cdot r_G^2 \\[5pt] &=& \pi\cdot (6\,\text{m})^2 \\[5pt] &=& 113,1\,\text{m}^2 \end{array}$

Nun kann der prozentuale Anteil berechnet werden.

$\text{Grundwert } G=113,1\,\text{m}^2$

$\text{Prozentwert } W=84,9\,\text{m}^2$

$\begin{array}[t]{rll} p\,\%&=& \dfrac{W}{G}\cdot 100\,\% \\[5pt] p\,\%&=& \dfrac{84,9\,\text{m}^2}{113,1\,\text{m}^2}\cdot 100\,\% \\[5pt] p\,\%&\approx& 75\,\% \end{array}$

Ca. $75\,\%$ der Grundfläche kann für Stehplätze genutzt werden.

12.1

Die Geamtlänge in Abhängigkeit von $x$ lässt sich wie folgt berechnen:

Rechenweg anzeigen

$\ell (x)=16x+20\,\text{cm}$

Für $x=18,5\,\text{cm}$ folgt:

$\ell(18,5\,\text{cm})=16\cdot 18,5\,\text{cm}+20\,\text{cm}=316\,\text{cm}$

Für $x=18,5\,\text{cm}$ beträgt die Gesamtlänge der benötigten Metallschienen $316\,\text{cm}.$

12.2

Umformen der Gleichung in Normalform:

$\begin{array}[t]{rll} 2x^2+12x+20 &=& x^2 \quad \scriptsize \mid\;-x^2 \\[5pt] x^2 +12x +20 &=& 0 \\[5pt] \end{array}$

Es gilt $p=12$ und $q=20.$ mit der Lösungsformel folgt:

$\begin{array}[t]{rll} x_{1/2}&=& -\dfrac{12}{2}\pm \sqrt{\left( \dfrac{12}{2}\right)^2 -20} \\[5pt] &=& -6\pm \sqrt{16} \\[5pt] &=& -6\pm 4\\[5pt] x_1&=& -6-4 \\[5pt] &=& -10 \\[10pt] x_2&=& -6+4\\[5pt] &=& -2 \end{array}$

Die Gleichung hat die Lösungen $x_1=-10$ und $x_2=-2.$

12.3

Alter von Lea: $x$
Alter von Leas Vater: $3x$
Alter von Leas Bruder: $x-4$

Damit ergibt sich die folgende Gleichung:

$\begin{array}[t]{rll} x + 3 x + x-4 &=& 76 \\[5pt] 5x-4&=& 76 &\quad \scriptsize \mid\;+4 \\[5pt] 5x&=& 80 &\quad \scriptsize \mid\;:5 \\[5pt] x &=& 16 \end{array}$

Lea ist demnach $16$ Jahre alt. Ihr Bruder ist vier Jahre jünger, also $12$ Jahre alt. Leas Vater ist dreimal so alt wie sie, also $3\cdot 16 = 48$ Jahre.