Teil A
In den Aufgaben 1 bis 6 ist von den jeweils fünf Auswahlmöglichkeiten genau eine Antwort richtig. Kreuze das jeweilige Feld an.
 von
von  sind
sind
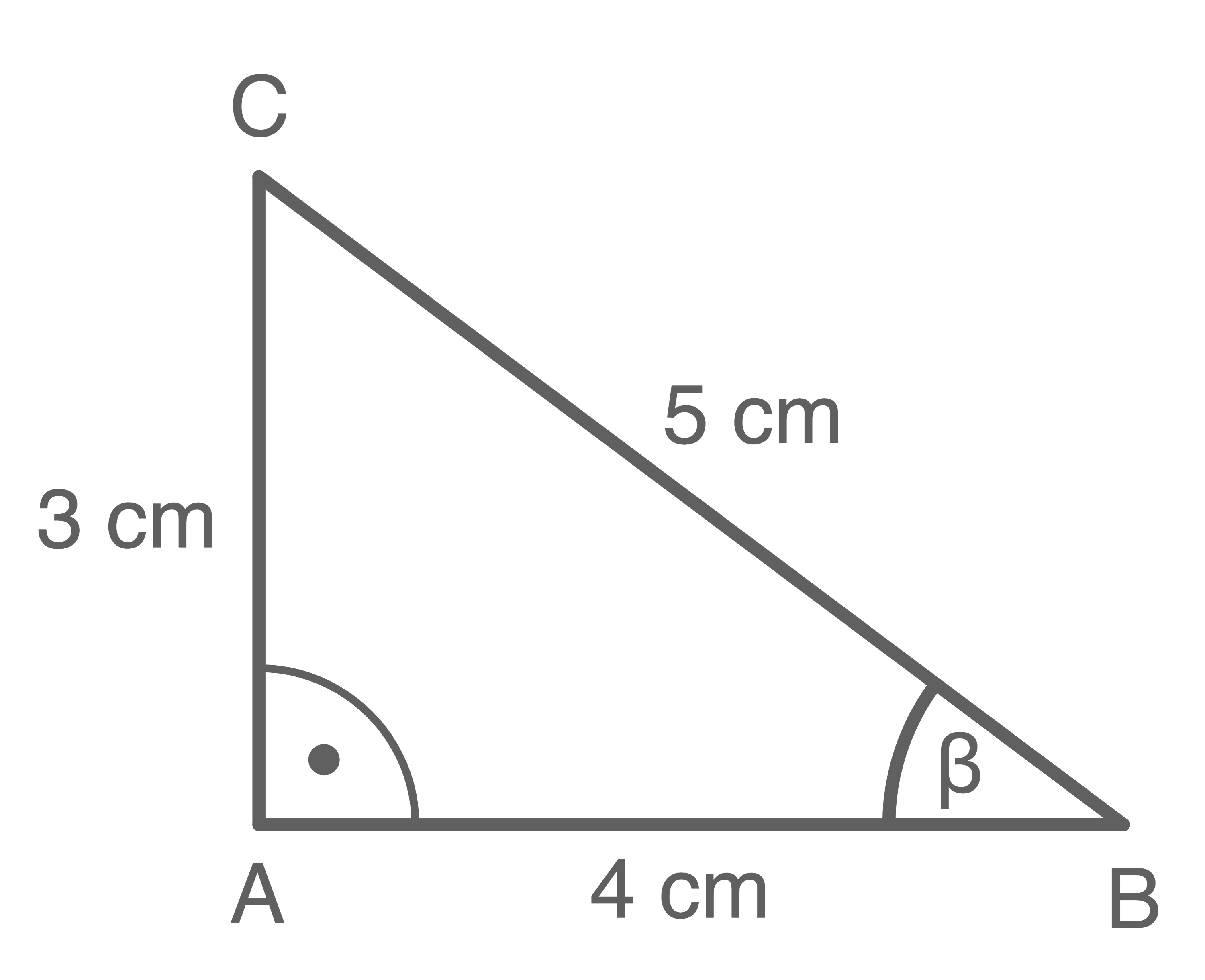 Im Dreieck
Im Dreieck  (siehe Abbilung) gilt für den Winkel
(siehe Abbilung) gilt für den Winkel 
 mit
mit 

1
(1 BE)
2
Welche Funktion besitzt keine Nullstelle?
(1 BE)
3
Welche Funktion besitzt für  die kleinste Periode
die kleinste Periode 
(1 BE)
4

(1 BE)
5
Die Kugel  besitzt das Volumen
besitzt das Volumen  Das Volumen
Das Volumen  der Kugel
der Kugel  mit doppelt so großem Radius wie
mit doppelt so großem Radius wie  beträgt:
beträgt:
(1 BE)
6
Eine Person wählt aus den natürlichen Zahlen von  bis
bis  eine Zahl zufällig aus.
eine Zahl zufällig aus.
Die Wahrscheinlichkeit dafür, dass diese gewählte Zahl gerade und durch teilbar ist, beträgt:
teilbar ist, beträgt:
Die Wahrscheinlichkeit dafür, dass diese gewählte Zahl gerade und durch
(1 BE)
7
Gegeben ist die Funktion
7.1
Gib die Nullstelle der Funktion  an.
Gib die Koordinaten des Schnittpunktes des Graphen von
an.
Gib die Koordinaten des Schnittpunktes des Graphen von  mit der
mit der  -Achse an.
-Achse an.
(2 BE)
7.2
Untersuche, ob der Punkt  auf dem Graphen der Funktion
auf dem Graphen der Funktion  liegt.
liegt.
(2 BE)
7.3
Der Graph der Funktion  entsteht durch Spiegelung des Graphen von
entsteht durch Spiegelung des Graphen von  an der
an der  -Achse.
-Achse.
Gib eine Gleichung der Funktion an.
an.
Gib eine Gleichung der Funktion
(1 BE)
8
Die Punkte  und
und  liegen auf dem Halbkreis über der Strecke
liegen auf dem Halbkreis über der Strecke  (siehe Abbildung).
(siehe Abbildung).
Berechne die Größe des Winkels
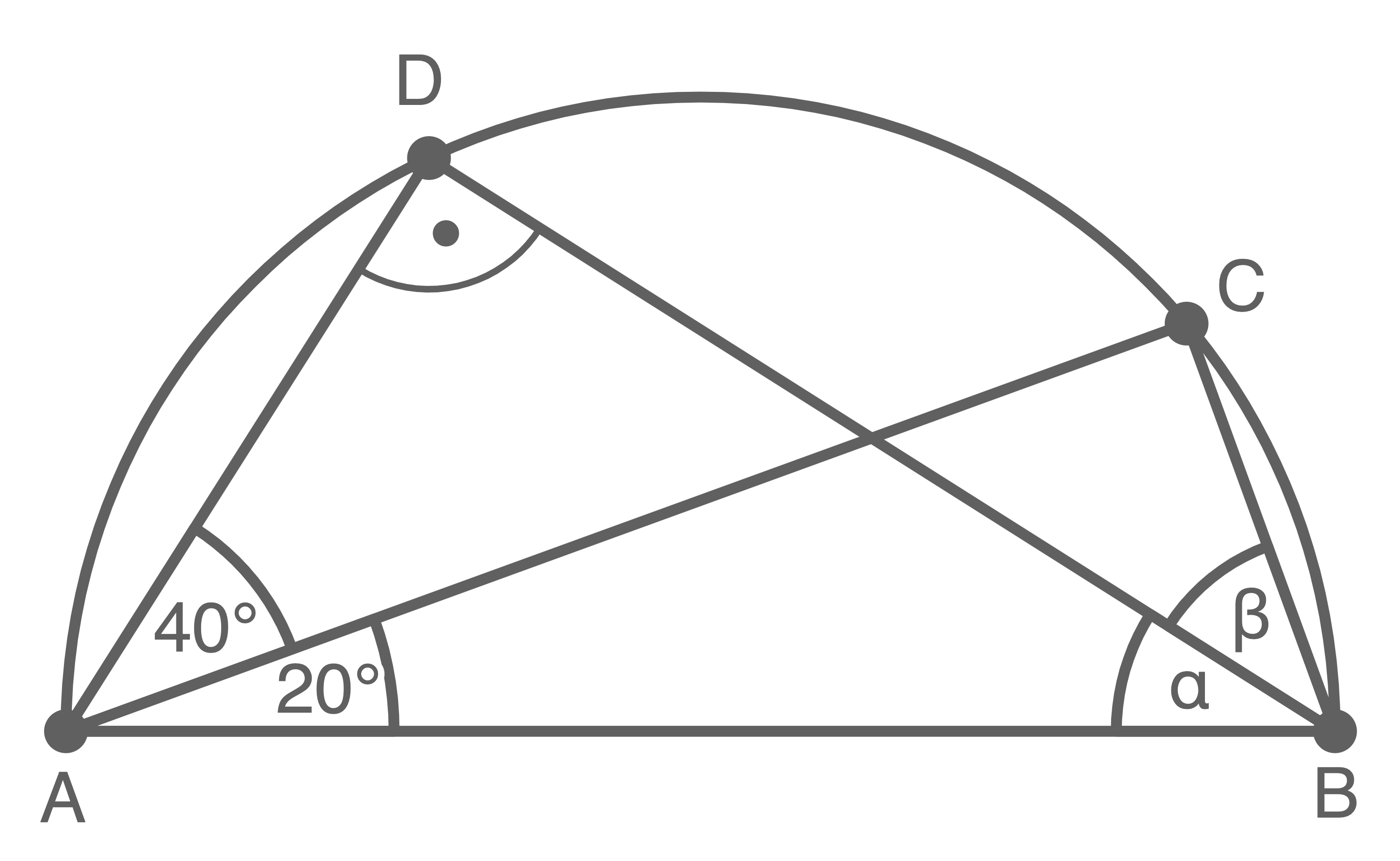
Berechne die Größe des Winkels

Abbildung (nicht maßstäblich)
(2 BE)
9
Löse die Gleichung  für
für 
(2 BE)
1
2
Aufgrund der Wurzel kann die dritte angegebene Funktion  nur Werte annehmen, die größer oder gleich
nur Werte annehmen, die größer oder gleich  sind.
Die dritte Antwortmöglichkeit ist die richtige.
sind.
Die dritte Antwortmöglichkeit ist die richtige.
3
Eine Funktion der Form  besitzt die Periode
besitzt die Periode  Die vierte angegebene Funktion
Die vierte angegebene Funktion  besitzt die Periode
besitzt die Periode  Dies entspricht der Funktion mit der kleinsten Periode
Dies entspricht der Funktion mit der kleinsten Periode  Die vierte Antwortmöglichkeit ist die richtige.
Die vierte Antwortmöglichkeit ist die richtige.
4
Das angegebene Dreieck ist rechtwinklig. Dafür gilt:
![\(\begin{array}[t]{rll}
\sin \beta &=& \dfrac{\text{Gegenkathete}}{\text{Hypotenuse}} \\[5pt]
&=& \dfrac{3}{5}\\[10pt]
\cos \beta&=& \dfrac{\text{Ankathete}}{\text{Hypotenuse}} \\[5pt]
&=& \dfrac{4}{5}\\[10pt]
\tan \beta &=& \dfrac{\text{Gegenkathete}}{\text{Ankathete}} \\[5pt]
&=& \dfrac{3}{4}\\[10pt]
\end{array}\)](https://www.schullv.de/resources/formulas/c7b8ee28cec8fd812a3a93fea1c9f077e18f38137916a5f11550755eac0dac4b_light.svg) Die vierte Antwortmöglichkeit ist die richtige.
Die vierte Antwortmöglichkeit ist die richtige.
5
Bezeichnen wir den Radius der Kugel  mit
mit  und den von
und den von  mit
mit  dann gilt
dann gilt  Mit der Volumenformel einer Kugel gilt:
Mit der Volumenformel einer Kugel gilt:
![\(\begin{array}[t]{rll}
V_1&=& \dfrac{4}{3}\cdot \pi \cdot r_1 ^3 \\[10pt]
V_2&=& \dfrac{4}{3}\cdot \pi \cdot r_2^3 \quad \scriptsize \mid\; r_2 = 2\cdot r_1 \\[5pt]
&=& \dfrac{4}{3}\cdot \pi \cdot \left(2\cdot r_1\right)^3 \\[5pt]
&=& \dfrac{4}{3}\cdot \pi \cdot 8\cdot r_1^3 \\[5pt]
&=& 8\cdot \dfrac{4}{3}\cdot \pi \cdot r_1^3 \\[5pt]
&=& 8\cdot V_1
\end{array}\)](https://www.schullv.de/resources/formulas/c57bfabc4818687717242e334f76a00e04157488644e26cd3254343734c1dbcd_light.svg) Die vierte Antwortmöglichkeit ist die richtige.
Die vierte Antwortmöglichkeit ist die richtige.
6
Von den natürlichen Zahlen von  bis
bis  sind folgende Zahlen gerade und durch
sind folgende Zahlen gerade und durch  teilbar:
teilbar:


 und
und  Die Wahrscheinlichkeit, eine solche Zahl zu ziehen, beträgt also:
Die Wahrscheinlichkeit, eine solche Zahl zu ziehen, beträgt also:
 Die zweite Antwortmöglichkeit ist die richtige.
Die zweite Antwortmöglichkeit ist die richtige.
7.1
Nullstellen angeben
![\(\begin{array}[t]{rll}
f(x)&=&0 \\[5pt]
2^x-2&=&0 \quad \scriptsize \mid\;+2 \\[5pt]
2^x&=& 2 \\[5pt]
x&=& 1
\end{array}\)](https://www.schullv.de/resources/formulas/d69526e46aee36a97dbe3337e5eed46e0f28d4d9f617b0517432d1b6ad5243b1_light.svg) Die Nullstelle der Funktion
Die Nullstelle der Funktion  ist
ist  Koordinaten des Schnittpunkts angeben
Koordinaten des Schnittpunkts angeben
![\(\begin{array}[t]{rll}
f(0)&=&2^0 -2 \\[5pt]
&=&1-2 \\[5pt]
&=&-1 \\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/712a9b72c4fcd1cac205fd1c0690f9c4f21f8db774599119bff7c4d279287569_light.svg) Der Graph von
Der Graph von  schneidet die
schneidet die  -Achse im Punkt
-Achse im Punkt 
7.2
7.3
Eine Spiegelung des Graphen von  entsteht durch ein negatives Vorzeichen vor dem
entsteht durch ein negatives Vorzeichen vor dem 
 Eine mögliche Funktionsgleichung von
Eine mögliche Funktionsgleichung von  lautet
lautet 
8
Da die Winkelsumme eines Dreiecks immer  beträgt, folgt für
beträgt, folgt für 
![\(\begin{array}[t]{rll}
180^{\circ}&=& 90^{\circ}+40^{\circ} +20^{\circ} +\alpha \\[5pt]
180^{\circ}&=& 150^{\circ} +\alpha \quad \scriptsize \mid\; -150^{\circ}\\[5pt]
30^{\circ}&=& \alpha\\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/0aa625bdb33761b76748cbac5a396129b30f2433590046fd907d3fedbd8b1b1c_light.svg) Wegen des Satz des Thales besitzt das Dreieck
Wegen des Satz des Thales besitzt das Dreieck  bei
bei  ebenfalls einen rechten Winkel. Mit der Winkelsumme ergibt sich daher:
ebenfalls einen rechten Winkel. Mit der Winkelsumme ergibt sich daher:
![\(\begin{array}[t]{rll}
180^{\circ}&=& 90^{\circ}+30^{\circ} +20^{\circ} +\beta \\[5pt]
180^{\circ}&=& 140^{\circ} +\beta \quad \scriptsize \mid\; -140^{\circ}\\[5pt]
40^{\circ}&=& \beta\\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/cae7bbf09c6d10e1cf5437d8e6290a55041d8136ffdc4f5fbe4f5ee8d877db3c_light.svg) Der Winkel
Der Winkel  ist
ist  groß.
groß.
9