Teil A

In den Aufgaben 1 bis 6 ist von den jeweils fünf Auswahlmöglichkeiten genau eine Antwort richtig. Kreuze das jeweilige Feld an.

Der Term $a^\frac{2}{3}$ mit $a\in\mathbb{R^+}$ ist äquivalent zum Term:

	$\sqrt{a^3}$
	$\sqrt[3]{a^2}$
	$a^{-\frac{3}{2}}$
	$\dfrac{1}{\sqrt{a^3}}$
	$\dfrac{1}{\sqrt[3]{a^2}}$

(1 BE)

$\dfrac{1}{10}$ von $2\,\text{m}^2$ sind:

	$0,02\,\text{m}^2$
	$0,1\,\text{m}^2$
	$1,9\,\text{m}^2$
	$2\,\text{dm}^2$
	$20\,\text{dm}^2$

(1 BE)

Welche Gleichung beschreibt eine Funktion mit der Nullstelle $x_N=1?$

	$f(x)=2^x-2$
	$f(x)=2^x-1$
	$f(x)=2^x$
	$f(x)=2^x+1$
	$f(x)=2^x+2$

(1 BE)

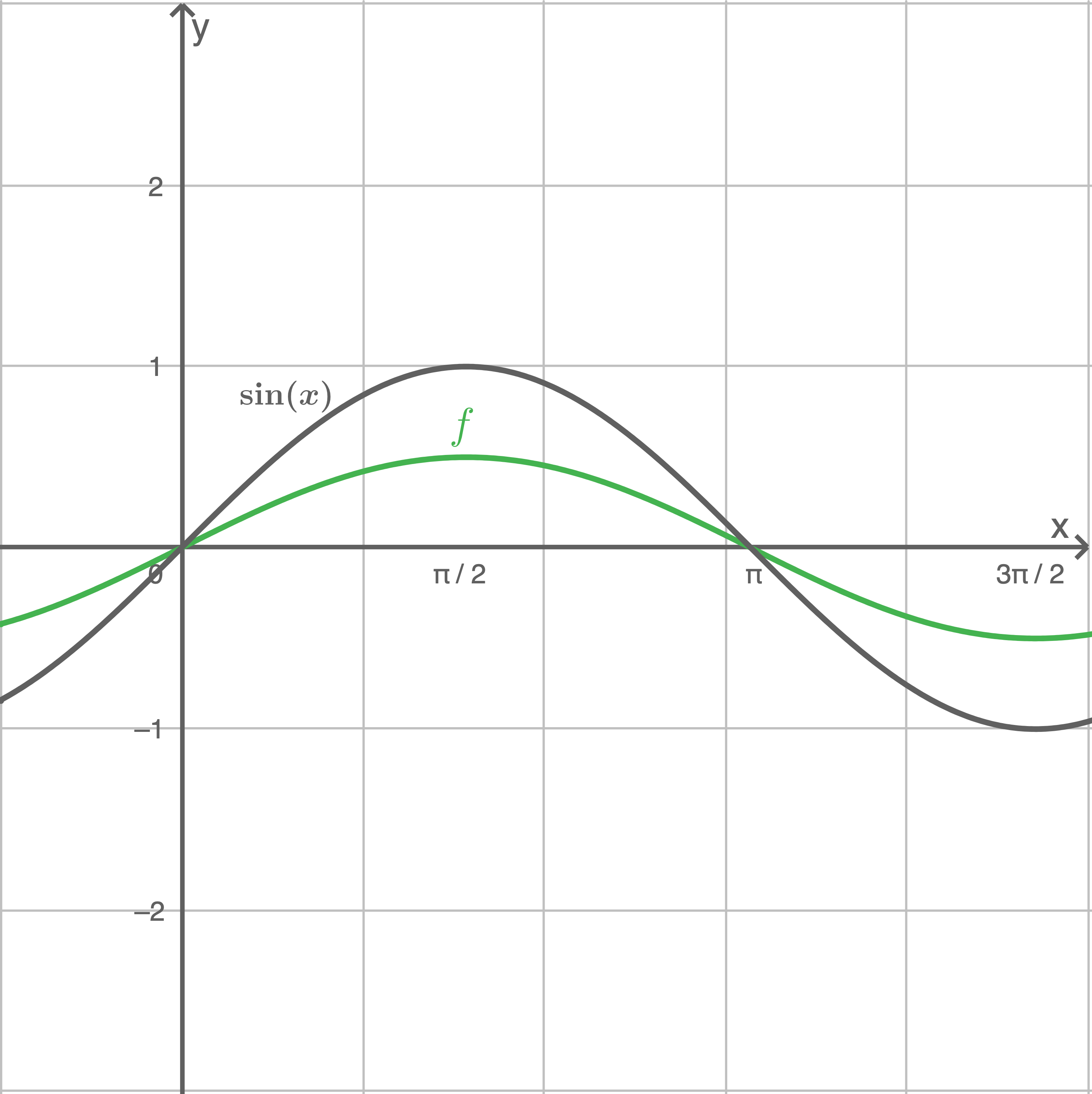
Für die in $\mathbb R$ definierte Funktion $f$ : $\mapsto \dfrac{1}{2}\cdot \sin(x)$ gilt:

	Der Graph von $f$ ist symmetrisch zur $y$ -Achse.
	$f$ hat den Wertebereich $W_f=\{y\,\vert\, y\in\mathbb R;-1\leq y\leq 1\}.$
	Die kleinste Periode von $f$ beträgt $4\cdot \pi.$
	Im Intervall $0\leq x\leq \dfrac{\pi}{2}$ ist $f$ monoton steigend.
	Der Graph von $f$ schneidet die y-Achse im Punkt $\left(0\mid \frac{1}{2}\right).$

(1 BE)

Das lineare Gleichungssystem $\begin{vmatrix}y=2\cdot x-1\\y=3\cdot x-1\end{vmatrix}$ besitzt die Lösung:

	$x=-1;y=0$
	$x=0;y=0$
	$x=0;y=-1$
	$x=2;y=-1$
	$x=3;y=-1$

(1 BE)

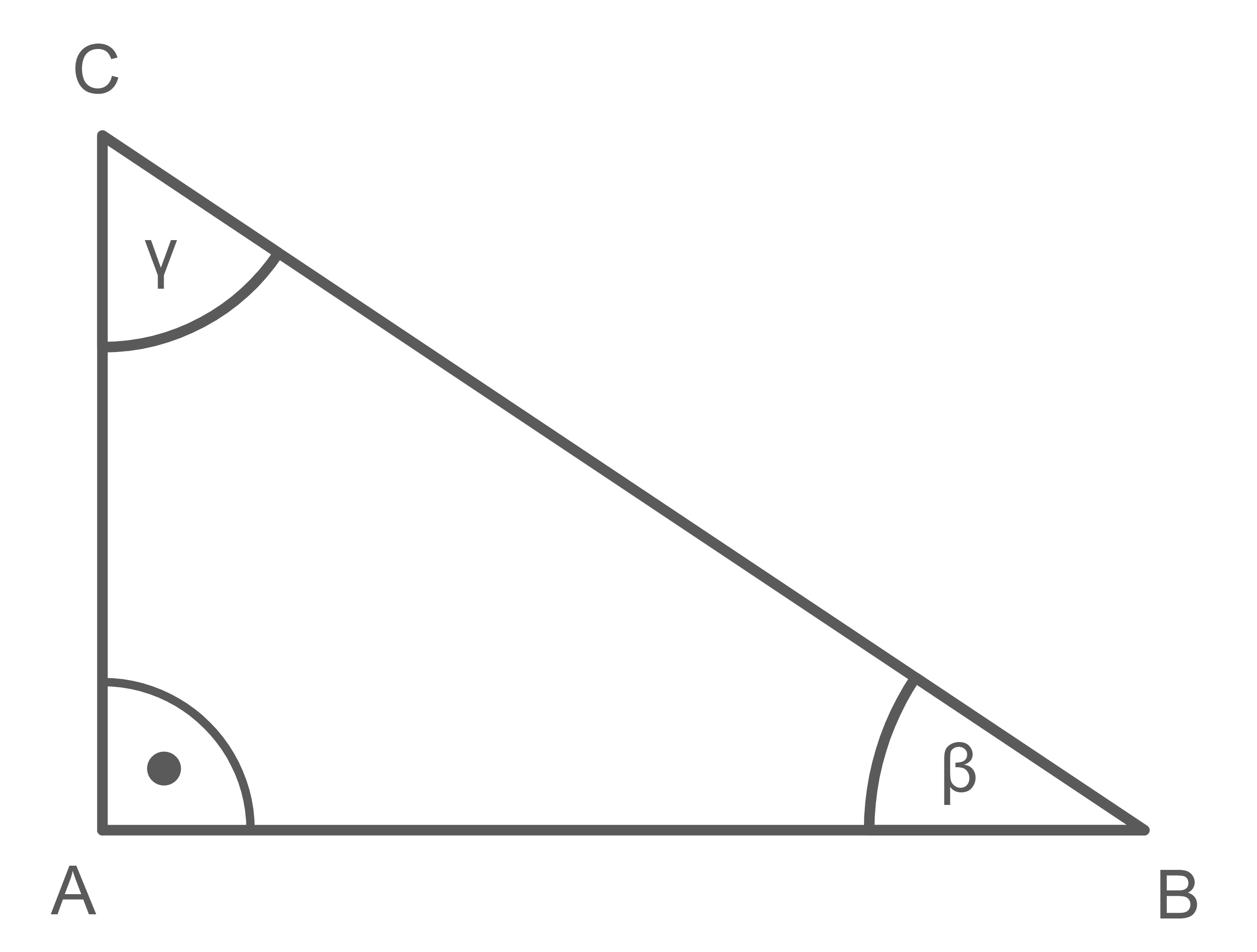
Welche Aussage zum abgebildeten Dreieck $ABC$ ist falsch?

	$\beta+\gamma=90°$
	$\overline{AB}+\overline{AC}\gt\overline{BC}$
	$\sin \gamma=\dfrac{\overline{AB}}{\overline{BC}}$
	$\cos \beta= \dfrac{\overline{AB}}{\overline{BC}}$
	$\tan \beta=\dfrac{\overline{AB}}{\overline{AC}}$

(1 BE)

Ein Glücksrad besteht aus drei Kreissektoren, die blau, gelb bzw. rot bemalt sind. Der blaue und der gelbe Sektor besitzen jeweils einen Zentriwinkel von $90^\circ.$ Ein Zufallsversuch besteht im einmaligen Drehen des Glücksrads und dem Feststellen der erzielten Farbe.

7.1

Begründe, dass dieser Zufallsversuch kein Laplace-Versuch ist.

(1 BE)

7.2

Der Zufallsversuch wird dreimal durchgeführt. Berechne die Wahrscheinlichkeit dafür, dass dabei mindestens einmal die Farbe Gelb festgestellt wird.

(3 BE)

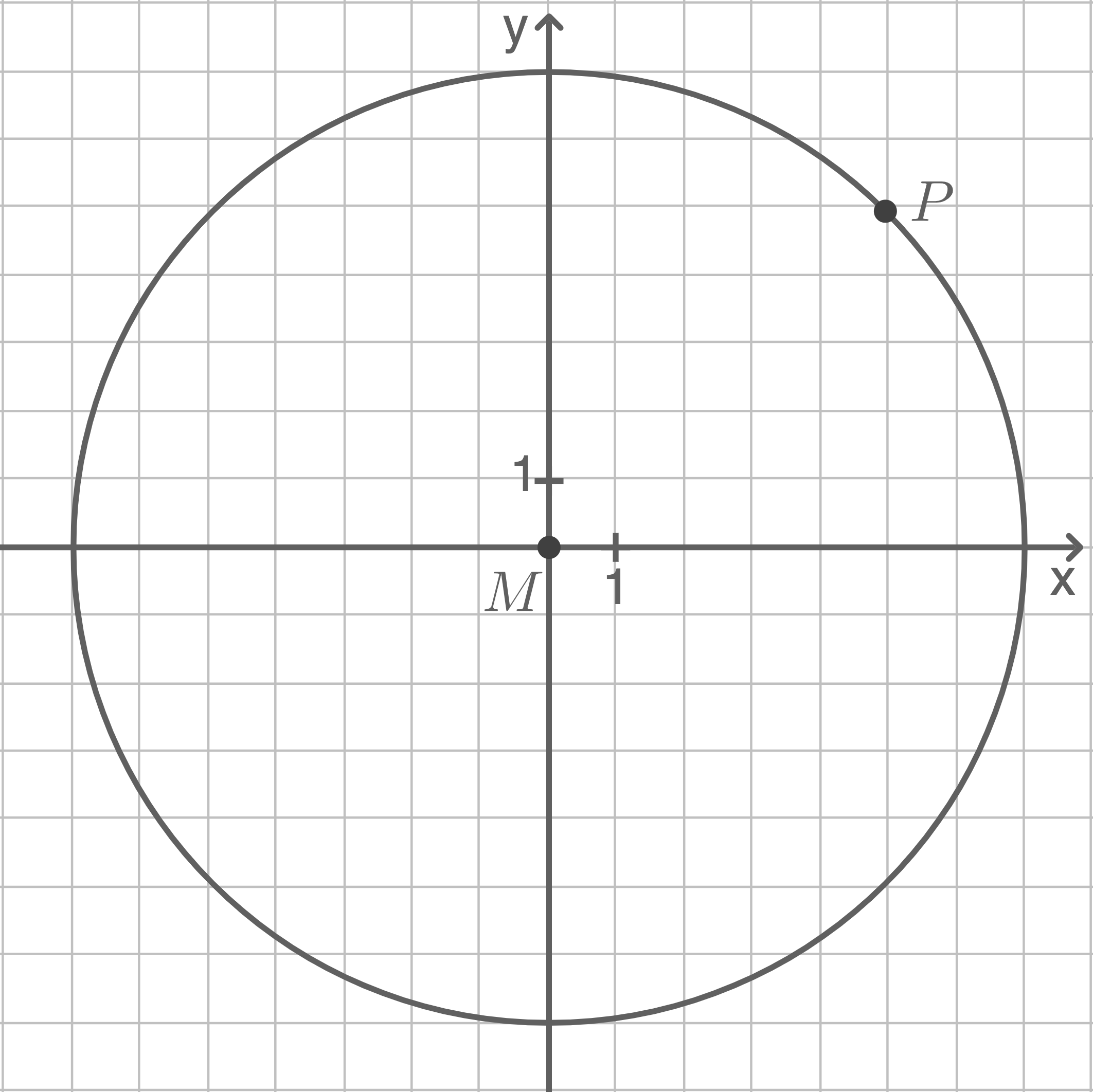
In einem Koordinatensystem wird der Kreis betrachtet, dessen Mittelpunkt $M$ im Koordinatenursprung liegt und der durch den Punkt $P (5\mid 5)$ verläuft.

8.1

Der Graph der linearen Funktion $g$ verläuft durch $M$ und $P.$

8.1.1

Gib eine Gleichung von $g$ an.

$\text{___________________________}$

(1 BE)

8.1.2

Der Halbkreis im ersten und zweiten Quadranten wird vom Graphen von $g$ in zwei Kreissektoren geteilt. Gib das Verhältnis der Flächeninhalte dieser beiden Kreissektoren an.

$\text{___________________________}$

(1 BE)

8.2

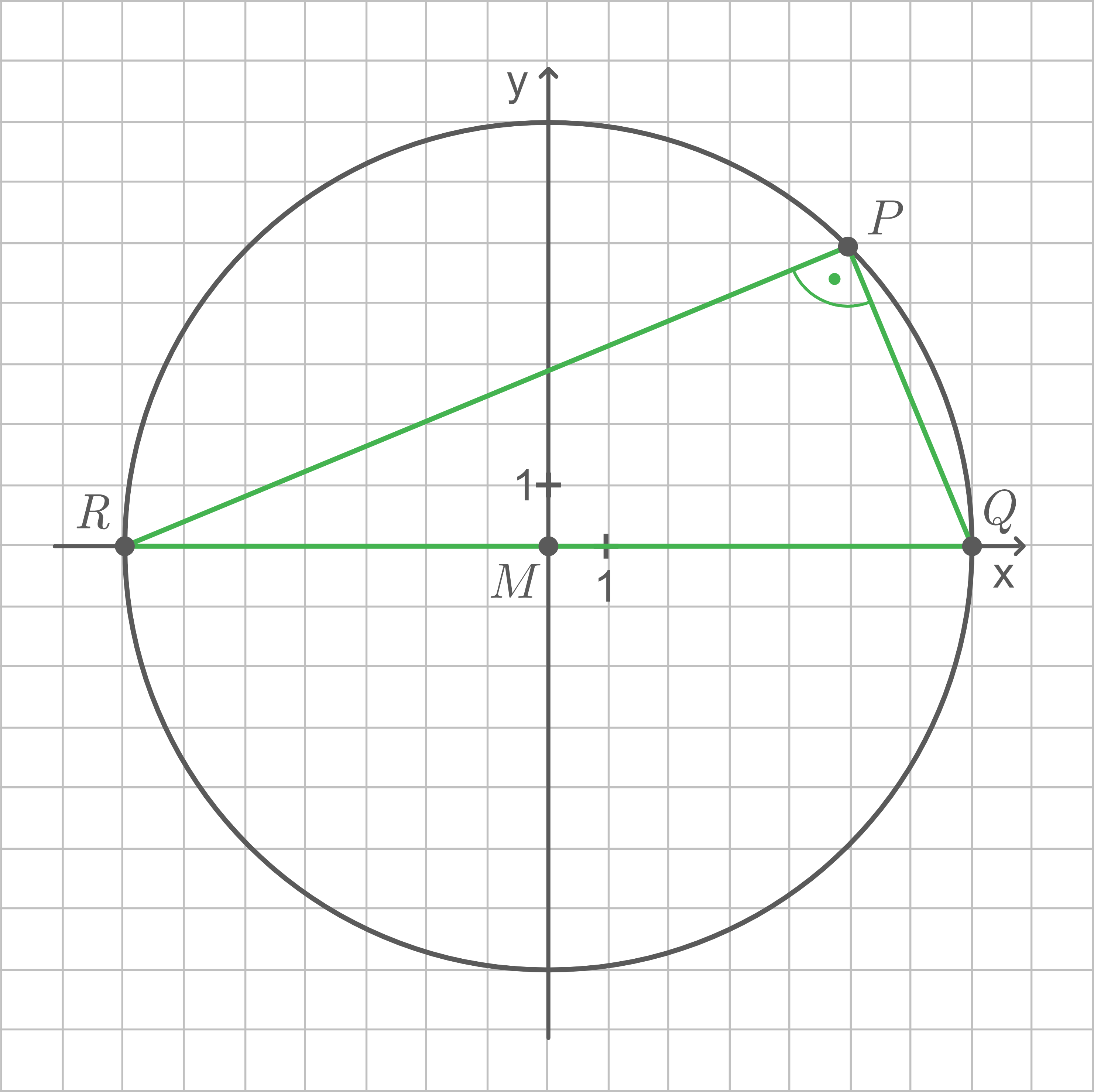
Auf dem Kreis liegen zwei weitere Punkte $R$ und $Q,$ sodass gilt: $\sphericalangle QPR=90^\circ.$

Berechne die Länge der Stecke $\overline{RQ}.$

(3 BE)

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?

$a^\frac{2}{3}=\sqrt[3]{a^2}$

$\dfrac{1}{10}\cdot 2\;\text{m}^2=0,2\;\text{m}^2=20\;\text{dm}^2$

$x=1$ in jede Funktion einsetzen und überprüfen bei welcher Funktion $f(1)=0$ gilt:

$f(1)=2^1-2=0$

$f(1)=2^1-1 \neq 0$

$f(1)=2^1 \neq 0$

$f(1)=2^1+1 \neq 0$

$f(1)=2^1+2 \neq 0$

Im Intervall $\left[0,\frac{\pi}{2}\right]$ nimmt der Sinus stetig zu und erreicht dort seinen Hochpunkt, daher ist die Sinusfunktion $\sin(x)$ dort monoton steigend.

Da $f(x)= \frac{1}{2}\cdot \sin(x)$ einen konstant positiven Vorfaktor hat, verändert dieser nur die Stauchung in $y$ -Richtung, aber nicht die Monotonie. Daher ist auch $f(x)=\frac{1}{2}\cdot \sin(x)$ in diesem Bereich monoton steigend.

Die linearen Gleichungen gleichsetzen und nach $x$ auflösen ergibt:

$\begin{array}[t]{rlll} 2\cdot x-1&=&3\cdot x-1 &\mid\;-2x \\[5pt] -1&=&x-1 &\mid\;+1 \\[5pt] 0&=&x \end{array}$

$x=0$ in eine der beiden Gleichungen einsetzen und nach $y$ auflösen:

$y=2\cdot 0-1=-1$

Die richtige Antwort ist also: $x=0; y=-1$

Im rechtwinkligen Dreieck gilt:

$\beta+ \gamma=90^\circ$
$\sin \gamma=\dfrac{\text{Gegenkathete}}{\text{Hypotenuse}}=\dfrac{\overline{AB}}{\overline{BC}}$
$\cos \beta=\dfrac{\text{Ankathete}}{\text{Hypotenuse}}=\dfrac{\overline{AC}}{\overline{BC}}$
$\tan \beta=\dfrac{\text{Gegenkathete}}{\text{Ankathete}}=\dfrac{\overline{AB}}{\overline{BC}}$

Somit ist die Antwort $\text{tan}\,\ \beta=\dfrac{\overline{AB}}{\overline{AC}}$ falsch.

7.1

Ein Laplace-Versuch liegt vor, wenn alle möglichen Ergebnisse gleichwahrscheinlich sind. Dieser Zufallsversuch ist kein Laplace-Versuch, da die möglichen Ergebnisse (Blau, Gelb, Rot) nicht gleichwahrscheinlich sind. Der rote Sektor ist doppelt so groß wie die anderen:

$P(\text{Blau})=\dfrac{90^\circ}{360^\circ}=\dfrac{1}{4}$
$P(\text{Gelb})=\dfrac{90^\circ}{360^\circ}=\dfrac{1}{4}$
$P(\text{Rot})=\dfrac{360^\circ-2\cdot90^\circ}{360^\circ}=\dfrac{1}{2}$

7.2

Gegenereignis: $P(\text{kein Gelb})= \left(\dfrac{3}{4}\right)^3=\dfrac{27}{64}$

$P(\text{mind. einmal Gelb})=1-\dfrac{27}{64}=\dfrac{37}{64}$

8.1

8.1.1

$g(x)=x$

8.1.2

Der Graph von $g$ teilt den Viertelkreis im ersten Quadranten in zwei gleichgroße Hälften. Damit ist ein Kreissektor $\frac{3}{4}$ groß und der andere $\frac{1}{4}.$ Das Verhältnis der beiden Kreissektoren ist somit $3:1.$

8.2

Da für $\sphericalangle QPR=90^\circ$ gilt und $P$ auf dem Kreis liegt, muss die Strecke $\overline{RQ}$ der Durchmesser des Kreises sein.

Radius $\boldsymbol{r}$ berechnen

$r=\sqrt{5^2+5^2}=\sqrt{50}=5\sqrt{2}$

Durchmesser $\boldsymbol{d}$ berechnen

$\overline{RQ}=d=2\cdot r=2\cdot 5\sqrt{2}=10\sqrt{2}$

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?