Teil A

In den Aufgaben 1 bis 6 ist von den jeweils fünf Auswahlmöglichkeiten genau eine Antwort richtig. Kreuze das jeweilige Feld an.

Welche der folgenden Funktionen mit $x \in D_f$ ist eine Exponentialfunktion?

	$f(x)=2\cdot x+3$
	$f(x)=x^2+1$
	$f(x)=x^3$

	$f(x)=2^x$
	$f(x)= \dfrac{1}{x^2}$

(1 BE)

Die Funktion $f$ mit $f(x)= \dfrac{1}{x-2}$ besitzt den größtmöglichen Definitionsbereich:

	$\{x \mid x\in\mathbb{R} , x\leq -2\}$
	$\{x \mid x\in \mathbb{R}, x\neq -2\}$
	$\{x \mid x\in\mathbb{R}, x \neq 0\}$

	$\{x \mid x\in\mathbb{R}, x \neq 2\}$
	$\{x \mid x\in\mathbb{R}, x \geq 2\}$

(1 BE)

Die Lösungen der Gleichung $x^2-4\cdot x-2=0$ sind:

	$x_1=-4+\sqrt{18}$ $x_2=-4-\sqrt{18}$
	$x_1=4+\sqrt{18}$ $x_2=4-\sqrt{18}$
	$x_1=-2+\sqrt{6}$ $x_2=-2-\sqrt{6}$

	$x_1=2+\sqrt{6}$ $x_2=2-\sqrt{6}$
	$x_1=2+\sqrt{2}$ $x_2=2-\sqrt{2}$

(1 BE)

Welches lineare Gleichungssystem besitzt mit $x\in\mathbb{R}$ und $y\in\mathbb{R}$ keine Lösung?

	$\begin{vmatrix}y=2\cdot x+1\\y=-2\cdot x+1\end{vmatrix}$
	$\begin{vmatrix}y=2\cdot x+1\\y=2\cdot x+1\end{vmatrix}$
	$\begin{vmatrix}y=2\cdot x+1\\y=2\cdot x-1\end{vmatrix}$

	$\begin{vmatrix}y=3\cdot x-4\\y=2\cdot x+3\end{vmatrix}$
	$\begin{vmatrix}y=1\\x=2\end{vmatrix}$

(1 BE)

Ein Rechteck wird mit $16$ gleich großen Quadraten vollständig und ohne Überlappungen ausgelegt.
Wie viele gleichgroße Quadrate mit halb so langen Seiten sind notwendig, um dasselbe Rechteck vollständig und ohne Überlappung auszulegen.

	4
	8
	32

	64
	128

(1 BE)

Gegeben sind drei von vier Messwerten: $1,20 \, \text {m},$ $1,80 \, \text {m}$ und $1,40 \, \text {m}.$ Das arithmetische Mittel der vier Messwerte beträgt $1,50 \, \text {m}.$

Der vierte Messwert ist:

	$1,50 \, \text {m}$
	$1,60 \, \text {m}$
	$2,10 \, \text {m}$

	$3,00 \, \text {m}$
	$4,40 \, \text {m}$

(1 BE)

Vereinfache folgenden Term so weit wie möglich:

$6\cdot x^5 \cdot \left(-\dfrac{1}{2}\right)\cdot x^4$ .

(2 BE)

Die folgende maßstäbliche Abbildung zeigt ein achteckiges Glücksrad in einem Koordinatensystem mit dem Koordinatenursprung $O$ .

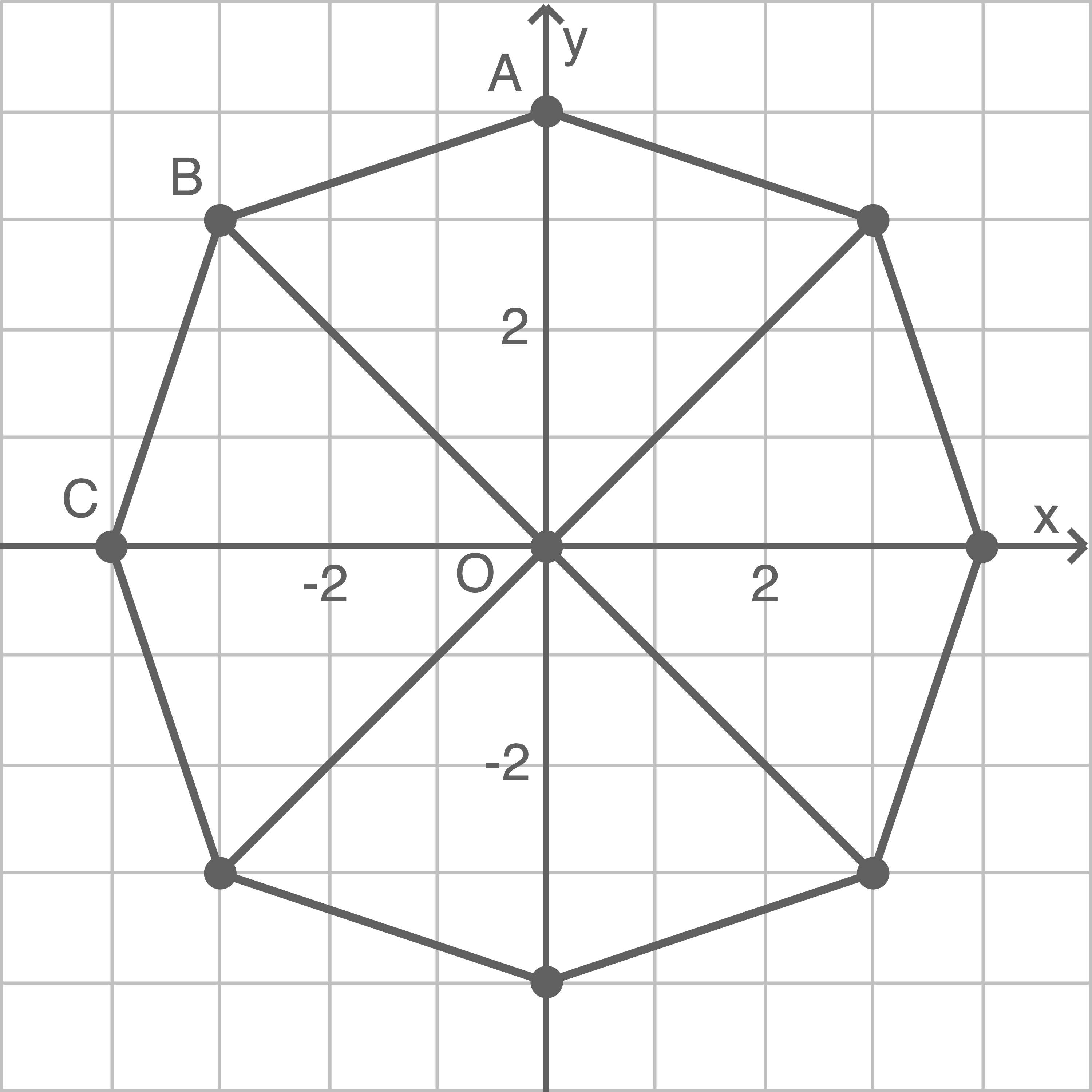Alle Eckpunkte des Achtecks haben ausschließlich ganzzahlige Koordinaten.

8.1

Gib die Koordinaten des Punktes $C$ an.

(1 BE)

8.2

Die Punkte $A$ und $B$ liegen auf einer Geraden.
Gib eine Gleichung dieser Geraden an.

(2 BE)

8.3

Begründe, dass die Dreiecke $COB$ und $BOA$ den gleichen Flächeninhalt haben.

(2 BE)

8.4

Nur das Dreieck $COB$ des Glücksrades ist rot gefärbt. Das Glücksrad wird zweimal gedreht. Berechne die Wahrscheinlichkeit dafür, dass dabei keinmal die Farbe Rot erzielt wird.

(2 BE)

Eine Exponentialfunktion ist eine Funktion, bei der die Funktionsvariable (hier $x$ ) im Exponenten vorkommt. Die einzige Antwortmöglichkeit, bei der dies der Fall ist, ist $f(x)=2^x.$

Die vierte Antwortmöglichkeit ist richtig.

Der Definitionsbereich wird dadurch eingeschränkt, dass der Nenner eines Bruchs nicht Null sein darf. Die Nullstelle des Nenners ist durch $x=2$ gegeben.

Der größtmögliche Definitionsbereich von $f$ ist also $\{ x\mid x\in \mathbb{R}, x\neq 2 \}.$

Die vierte Antwortmöglichkeit ist richtig.

Mit der $pq$ -Formel folgt:

$\begin{array}[t]{rll} x_{1/2} &=& -\dfrac{-4}{2}\pm \sqrt{\left(\dfrac{-4}{2} \right)^2 -(-2)} \\[5pt] &=& 2\pm \sqrt{(-2)^2 +2} \\[5pt] &=& 2\pm \sqrt{6} \\[5pt] \end{array}$

Die vierte Antwortmöglichkeit ist richtig.

Werden beim dritten Gleichungssystem beide Darstellungen für $y$ gleichgesetzt, ergibt sich:

$\begin{array}[t]{rll} y &=& y\\[5pt] 2\cdot x +1 &=& 2\cdot x -1 \quad \scriptsize \mid\; -2\cdot x\\[5pt] 1 &=& -1 \end{array}$

Dieses Gleichungssystem besitzt für $x \in \mathbb{R}$ und $y\in \mathbb{R}$ also keine Lösung.

Die dritte Antwortmöglichkeit ist richtig.

In ein großes Quadrat passen vier der kleinen Quadrate mit halber Seitenlänge. Das Rechteck wird mit $16$ großen Quadraten vollständig ausgelegt. Von den kleineren Quadraten benötigt man also:

$4\cdot 16 = 64$

Die vierte Antwortmöglichkeit ist richtig.

Der fehlende Messwert wird mit $x$ bezeichnet. Mit der Formel für das arithmetische Mittel folgt:

$\begin{array}[t]{rll} \dfrac{1,20 + 1,80 + 1,40 + x}{4}&=& 1,50 \\[5pt] \dfrac{4,40 + x }{4} &=& 1,50 \quad \scriptsize \mid\; \cdot 4 \\[5pt] 4,40 + x &=& 6,00 \quad \scriptsize \mid\;- 4,40 \\[5pt] x &=& 1,60 \end{array}$

Die zweite Antwortmöglichkeit ist richtig.

$\begin{array}[t]{rll} & 6\cdot x^5 \cdot \left(-\dfrac{1}{2} \right)\cdot x^4\\[5pt] =& -3 \cdot x^5\cdot x^4\\[5pt] =& -3\cdot x^9 \end{array}$

8.1

$1$ Kästchen entspricht einer Einheit.

$C(-4\mid 0)$

8.2

Der Punkt $A$ liegt auf der $y$ -Achse $A(0\mid 4)$ und gibt daher direkt den $y$ -Achsenabschnitt der Geraden an:

$y = m\cdot x + 4$

Der Punkt $B$ hat die Koordinaten $B(-3\mid 3).$ Einsetzen der Koordinaten in die Geradengleichung liefert:

$\begin{array}[t]{rll} y &=& m\cdot x +4 \quad \scriptsize \mid\; B(-3\mid 3) \\[5pt] 3 &=& m\cdot (-3) +4 \quad \scriptsize \mid\; -4\\[5pt] -1 &=& m\cdot (-3) \quad \scriptsize \mid\; :(-3) \\[5pt] \dfrac{1}{3} &=& m \end{array}$

Eine Gleichung der Geraden, auf der $A$ und $B$ liegen, lautet:

$y = \dfrac{1}{3}x +4$

8.3

Der Flächeninhalt eines Dreiecks wird aus der Länge der Grundseite und der zugehörigen Höhe berechnet.

Die Seiten $\overline{OA}$ und $\overline{OC}$ sind jeweils $4$ Längeneinheiten lang und können als Grundseite interpretiert werden.

Die Höhe eines Dreiecks ist dann durch den Abstand von Punkt $B$ zur jeweiligen Grundseite gegeben. Der Abbildung kann entnommen werden, dass die Höhe in beiden Fällen $3$ Längeneinheiten entspricht.

Da die Länge der Grundseite und der Höhe der beiden Dreiecke gleich sind, haben sie folglich auch den gleichen Flächeninhalt.

8.4

Das Glücksrad besteht aus acht Feldern, wovon eines rot ist. Die Wahrscheinlichkeit dafür, dass bei einem Dreh nicht das rote Feld angezeigt wird, beträgt also $\frac{7}{8}.$ Es wird zweimal gedreht. Mit der Pfadmultiplikationsregel folgt:

$\dfrac{7}{8}\cdot \dfrac{7}{8} = \dfrac{49}{64}$

Beim zweimaligen Drehen wird mit einer Wahrscheinlichkeit von $\frac{49}{64}$ keinmal die Farbe Rot angezeigt.