Teil B

Gegeben ist die Funktion $f$ mit $f(x)= \dfrac{1}{(x+1)^2}$ in ihrem größtmöglichen Definitionsbereich.

1.1

Gib die Polstelle und den Wertebereich von $f$ an.

(2 BE)

1.2

Bestimme alle Argumente von $f,$ deren Funktionswert $4$ beträgt.

(3 BE)

1.3

Der Graph von $f$ und die Gerade $g$ mit $g(x)=2\cdot x+5$ haben zwei gemeinsame Punkte.

Bestimme den Abstand dieser beiden Punkte.

(3 BE)

1.4

Die Funktion $h$ mit $h(x)=\dfrac{1}{(x+a)^2}+b$ besitzt den Definitonsbereich $D_h=\{x\mid x \in\mathbb R;\; x\neq2\}$ und den Wertebereich $W_h=\{y\mid y \in\mathbb R;\;y\gt3\}.$

Gib die Werte von $a$ und $b$ an.

(2 BE)

Im Parallelogramm $ABCD$ ist der Punkt $M$ Mittelpunkt der Diagonalen $AC$ und $BD$ (siehe Abbildung).
Es gilt: $\overline{AC}=6\;\text{cm},\;$ $\overline{BD}=8\;\text{cm}$ und $\sphericalangle DMA=60^\circ.$

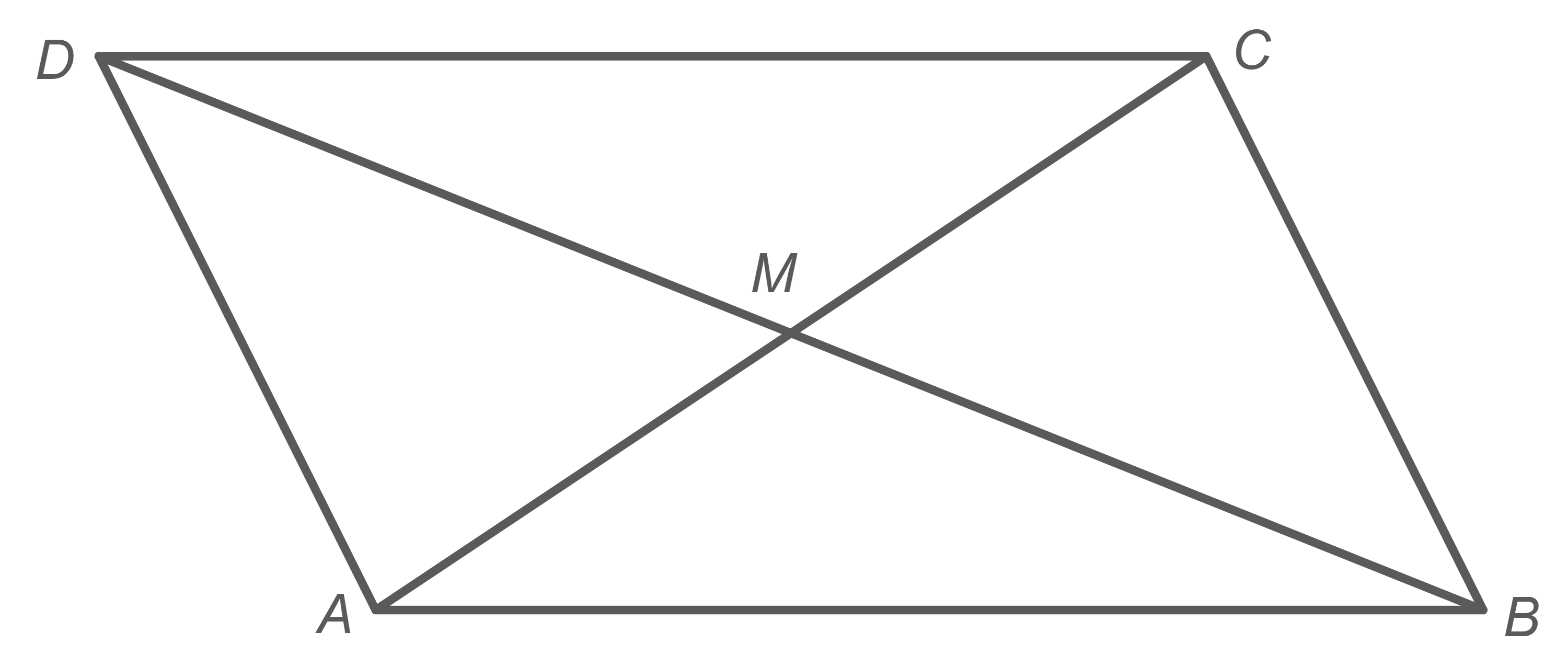
Viereck ABCD mit Diagonalen AC und BD und Schnittpunkt M

Abbildung (nicht maßstäblich)

2.1

Berechne die Länge der Strecke $\overline{AD}.$

(3 BE)

2.2

Zeige, dass die Flächeninhalte der Dreiecke $AMD$ und $ABM$ gleich groß sind.

(3 BE)

Die Hansestadt Hamburg zieht jährlich Millionen Touristen aus dem In- und Ausland an.

3.1

Im Jahr $2022$ hatte Hamburg $14,7$ Millionen touristische Übernachtungen zu verzeichnen, $21\,\%$ davon entfielen auf internationale Touristen. Der Anteil von Touristen aus Dänemark an diesen internationalen Übernachtungen betrug $12\,\%.$

Ermittle den prozentualen Anteil der Übernachtungen von Touristen aus Dänemark an den touristischen Übernachtungen.

(2 BE)

3.2

Für Fußgänger und Radfahrer führt ein $426,50\;\text{m}$ langer, geradliniger Tunnel unter der Elbe hindurch.

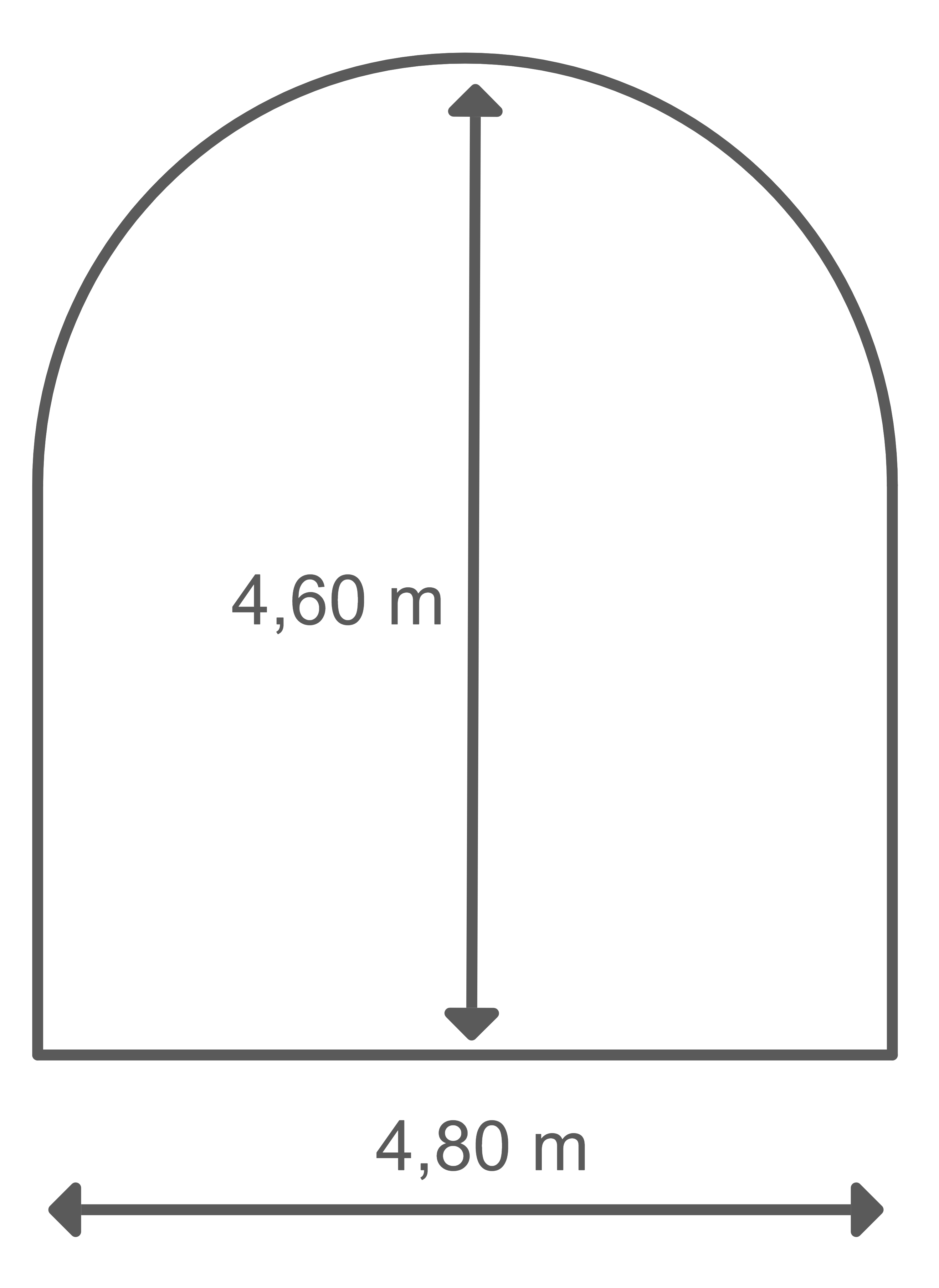
Die Abbildung 1 zeigt den Querschnitt des Tunnels, der die Form eines Rechtecks mit aufgesetztem Halbkreis hat. Die beiden Seitenwände und die gewölbte Decke sind auf der gesamten Tunnellänge vollständig gefliest.

Begründe, dass jede Seitenwand $2,20\;\text{m}$ hoch ist.

Berechne den Inhalt der gefliesten Fläche.

Skizze: Rechteck mit abgerundetem oberen Ende, Breite 4,80 m, Höhe 4,60 m.

Abbildung 1 (nicht maßstäblich)

(5 BE)

3.3

Besucher der Elbphilharmonie gelangen mithilfe einer bogenförmigen Rolltreppe vom Eingangsbereich zur Aussichtsebene.

3.3.1

Innerhalb von $10$ Sekunden wird ein auf der Rolltreppe stehender Besucher um $5$ Meter befördert. Die Fahrt vom Eingangsbereich zur Aussichtsebene dauert $2,7$ Minuten.

Berechne die Länge der Rolltreppe.

(3 BE)

Im Längsschnitt kann die Profillinie der Rolltreppe zwischen den Punkten $E(0\mid 0)$ und $A\bigl(75\mid f(75)\bigr)$ näherungsweise durch den Graphen der Funktion $f$ mit $f(x)=-\frac{13}{3750}\cdot x^2 + \frac{33}{50}\cdot x$ $\quad$ $(x\in \mathbb R,\;0\leq x \leq 75)$ beschrieben werden.
Die Profillinie der über der Rolltreppe befindlichen Decke kann durch den Graphen einer Funktion $g$ beschrieben werden (vgl. Abbildung 2).
Eine Längeneinheit im Koordinatensystem entspricht einem Meter in Wirklichkeit.

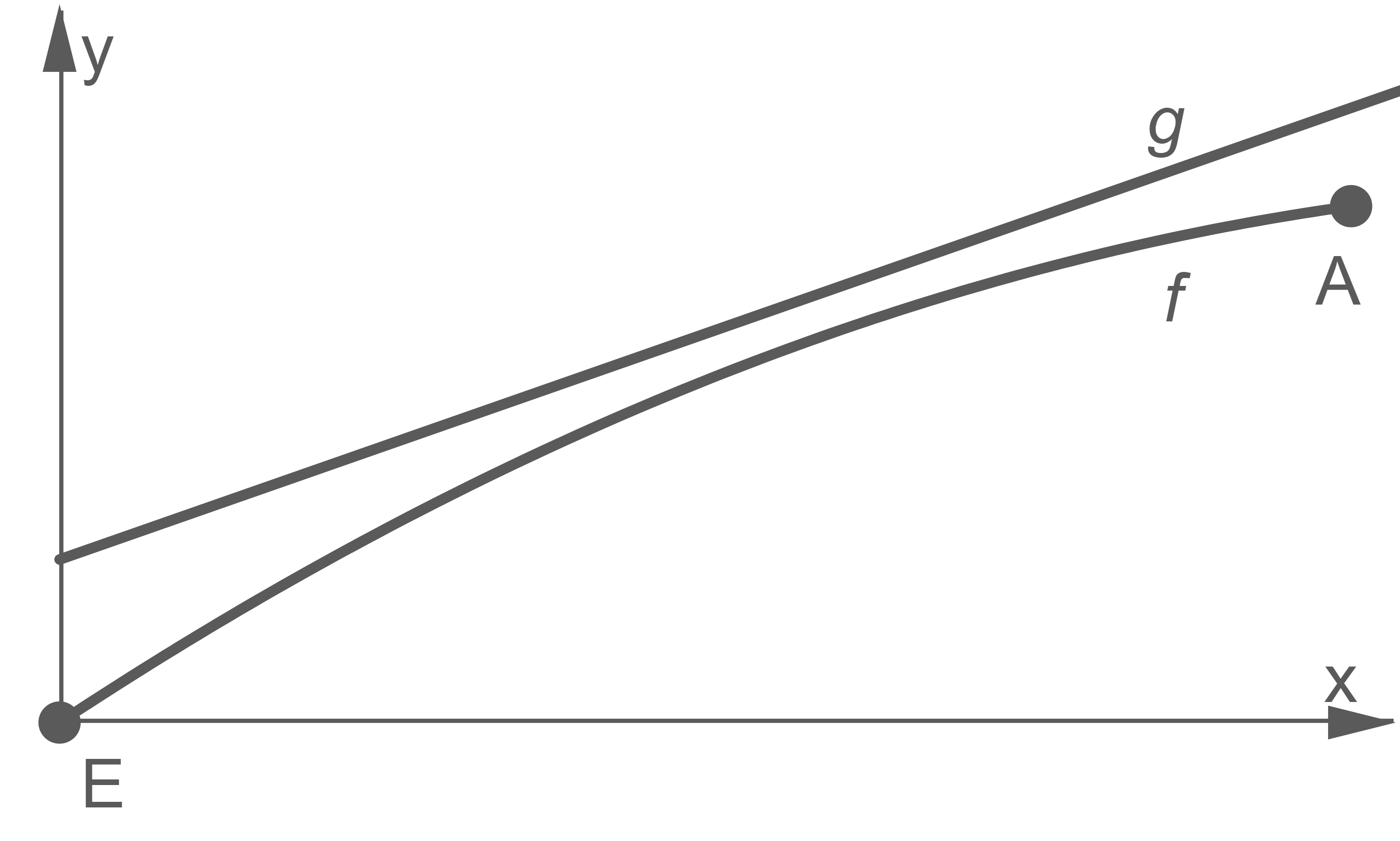
Koordinatensystem mit x- und y-Achse, zwei steigenden Kurven f und g und Punkt A rechts oben.

Abbildung 2 (nicht maßstäblich)

3.3.2

Ermittle den Höhenunterschied, der mithilfe der Rolltreppe vom Eingangsbereich zur Aussichtsebene überwunden wird.

(2 BE)

3.3.3

Auf dem Graphen von $f$ existiert ein Punkt $P\bigl(x_P\mid f(x_P)\bigr),$ für den die Differenz $g(x_P)-f(x_P)$ minimal ist.

Deute diese minimale Differenz im Sachzusammenhang.

(2 BE)

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?

1.1

Eine Polstelle tritt hier auf, wenn der Nenner Null wird:

$(x+1)^2=0$

Polstelle bei $x=-1.$

Der Nenner und der Zähler sind für alle $x$ -Werte positiv. Somit gilt:

Wertebereich: $W_f= \{y\in\mathbb R\mid y\gt0\}$

1.2

$\begin{array}[t]{rlll} f(x)&=&4 \\[5pt] \dfrac{1}{(x+1)^2}&=&4 &\mid\; \cdot\;(x+1)^2 \\[5pt] 1&=&4\cdot (x+1)^2 &\mid\; \text{Seiten tauschen} \\[5pt] 4\cdot (x+1)^2&=&1 &\mid\;:4 \\[5pt] (x+1)^2&=&\dfrac{1}{4} &\mid\;\sqrt{\;} \\[5pt] x+1 &=& ±\dfrac{1}{2} &\mid\;-1 \\[5pt] x_1&=&\dfrac{1}{2}-1=-\dfrac{1}{2} \\[5pt] x_2&=&-\dfrac{1}{2}-1=-\dfrac{3}{2} \end{array}$

Die Lösungen sind somit:

$x_1=-\dfrac{1}{2}$ und $x_2=-\dfrac{3}{2}$

1.3

Gemeinsame Punkte bestimmen:

$f(x)=g(x)$

$\dfrac{1}{(x+1)^2}=2x+5$

Der Taschenrechner liefert die Lösungen:

$x_1=-2$ und $x_2=-\dfrac{1}{2}$

$x_1$ und $x_2$ in die Funktion einsetzen, um $y$ -Werte der Punkte herauszufinden:

$f(-2)=1$ und $f\left(-\frac{1}{2}\right)=4$

Abstand zwischen den Punkten $P_1(-2\mid1)$ und $P_2\left(-\tfrac{1}{2}\mid4\right)$ berechnen:

$d=\sqrt{\left(-2-\left(-\dfrac{1}{2}\right)\right)^2+(1-4)^2}=\dfrac{3\sqrt{5}}{2}$

1.4

Aufgrund des Definitionsbereichs liegt eine Polstelle bei $x=2$ vor. Somit folgt:

$(2+a)^2=0$

Das liefert $a=-2.$

$h(x)=\dfrac{1}{(x-2)^2}+b$

Für $x\rightarrow2$ gilt $h(x)\rightarrow \infty$ aufgrund der Polstelle.

$\lim\limits_{x \rightarrow \infty} h(x) = 0+b$

Damit $h(x)\gt3$ für alle $x$ gilt, muss somit $b=3$ sein.

2.1

Die Länge der Strecke $\overline{AD}$ kann mithilfe des Kosinnussatzes berechnet werden:

$\left| \overline{AD} \right|= \sqrt{4^2+3^2-2\cdot 4\cdot 3\cdot \cos(60^\circ)}= \sqrt{13}$

2.2

Der Winkel $\sphericalangle AMB$ ergibt sich aus: $180^\circ-60^\circ=120^\circ.$ Damit folgt:

$A_{ABM}=\dfrac{1}{2}\cdot 3\cdot 4\cdot \sin(120^\circ)=3\sqrt{3}$

$A_{AMD}=\dfrac{1}{2}\cdot 3\cdot 4\cdot \sin(60^\circ)=3\sqrt{3}$

3.1

Prozentualer Anteil der Übernachtungen von Touristen aus Dänemark:

$0,21\cdot 0,12=0,0252=2,52\,\%$

3.2

Der Durchmesser des Halbkreises beträgt $d=4,80\;\text{m},$ dementsprechend ist der Radius $r=2,40\;\text{m}.$

Höhe der Wände:

$4,60-2,40=2,20\;[\text{m}]$

Für den Flächeninhalt der Wände gilt:

$A_1=2\cdot2,20\cdot 426,5=1876,6\;\left[\text{m}^2\right]$

Der Inhalt der gekrümmten Fläche wird mit dem Umfang $U$ des Halbkreises berechnet:

$\begin{array}[t]{rlll} A_2&=&U\cdot 426,5=\dfrac{1}{2}\cdot\pi\cdot d\cdot 426,5\\[5pt] &=&3215,7342\;\left[\text{m}^2\right] \end{array}$

Somit folgt für den gesamten Flächeninhalt der gefliesten Fläche:

$A_g=A_1+A_2=5092,2342\approx5092\;\left[\text{m}^2\right]$

3.3

3.3.1

$2,7\;\text{min}=2,7\cdot60=162\;[\text{s}]$

Da zehn Sekunden fünf Metern entsprechen, folgt:

$162\cdot\dfrac{5}{10}=81\;[\text{m}]$

3.3.2

$f(75)=30\;[\text{m}]$

3.3.3

Im Sachzusammenhang beschreibt $f(x)$ die tatsächliche Bahn der Rolltreppe, wohingegen $g(x)$ die Decke über der Rolltreppe beschreibt.

Der Punkt der minimalen Differenz $g(x_P)-f(x_P)$ beschreibt hierbei die kleinste Deckenhöhe über der Rolltreppe, also den kleinsten vertikalen Abstand zwischen der Rolltreppe und der Decke.

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?