Teil B
1
Gegeben ist die Funktion  mit
mit 

1.1
Bestimme die Koordinaten des Schnittpunkts des Graphen von  mit der
mit der  -Achse.
-Achse.
Gib den Wertebereich von an.
an.
Gib den Wertebereich von
(3 BE)
1.2
Ermittle das Argument zum Funktionswert 
(2 BE)
1.3
Der Punkt  liegt auf dem Graphen der Funktion
liegt auf dem Graphen der Funktion  mit
mit

 Bestimme den Wert von
Bestimme den Wert von 
(2 BE)
2
Gegeben ist das Dreieck  mit
mit 
 und
und 
Der Punkt ist Mittelpunkt des Umkreises des Dreiecks
ist Mittelpunkt des Umkreises des Dreiecks  (siehe Abbildung).
(siehe Abbildung).
Der Punkt
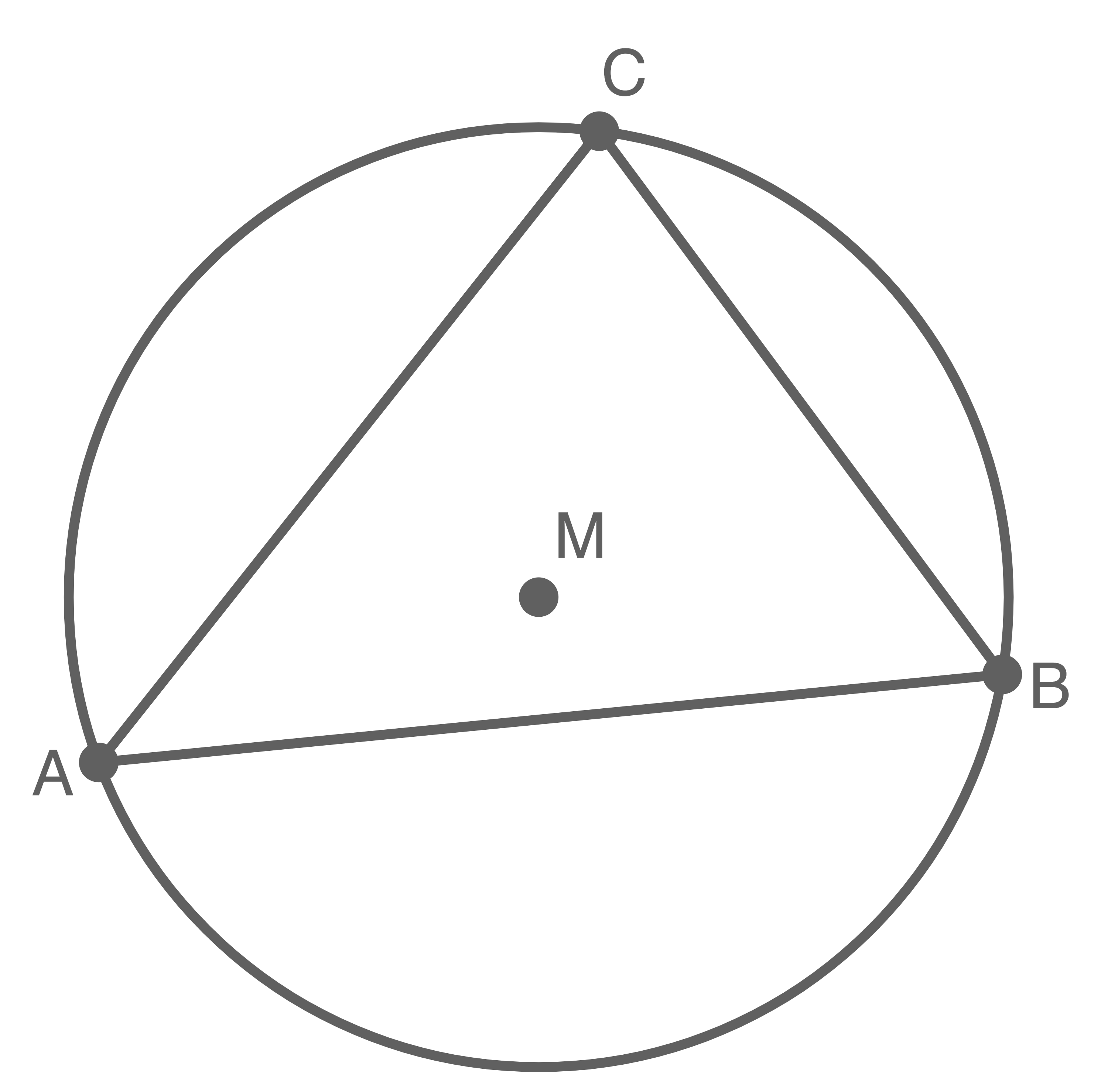
Abbildung (nicht maßstäblich)
2.1
Berechne die Länge der Seite 
(2 BE)
2.2
Die Größe des Winkels  beträgt
beträgt 
Zeige, dass gilt:
Zeige, dass gilt:
(3 BE)
2.3
Berechne den prozentualen Anteil des Flächeninhaltes des Dreiecks  am Flächeninhalt seines Umkreises.
am Flächeninhalt seines Umkreises.
(3 BE)
3
Ein Smartphonehersteller entwickelt ein neues Modell.
3.1
Ein herausragendes Produktmerkmal dieses Smartphones wird die kurze Ladedauer seines Akkus sein. Die Funktion  mit
mit 
 beschreibt in Abhängigkeit von der Restkapazität
beschreibt in Abhängigkeit von der Restkapazität  des Akkus zu Ladebeginn die Zeit bis zum vollständigen Aufladen des Akkus.
Dabei gilt:
des Akkus zu Ladebeginn die Zeit bis zum vollständigen Aufladen des Akkus.
Dabei gilt:
 ... Restkapazität des Akkus zu Ladebeginn in Prozent
... Restkapazität des Akkus zu Ladebeginn in Prozent
 ... Zeit bis zum vollständigen Aufladen des Akkus in Minuten bei der Restkapazität
... Zeit bis zum vollständigen Aufladen des Akkus in Minuten bei der Restkapazität 
3.1.1
Die Restkapazität eines Akkus dieses Smartphonemodells beträgt 
Zeige, dass die Zeit bis zum vollständigen Aufladen dieses Akkus Minuten beträgt.
Minuten beträgt.
Zeige, dass die Zeit bis zum vollständigen Aufladen dieses Akkus
(2 BE)
3.1.2
Ein Akku dieses Smartphonemodells wird innerhalb einer halben Stunde vollständig aufgeladen.
Ermittle die Restkapazität des Akkus zu Ladebeginn.
Ermittle die Restkapazität des Akkus zu Ladebeginn.
(3 BE)
3.1.3
Bestimme die Nullstelle der Funktion 
Interpretiere den Wert dieser Nullstelle im Sachzusammenhang.
Interpretiere den Wert dieser Nullstelle im Sachzusammenhang.
(3 BE)
3.2
Das neue Smartphonemodell wird in den Farben Silber und Weiß produziert.
Eine Prognose des Herstellers besagt, dass dieses Modell in aller Käufe von weiblichen und in
aller Käufe von weiblichen und in  aller Käufe von männlichen Käufern erworben wird.
aller Käufe von männlichen Käufern erworben wird.  der weiblichen Käufer kaufen ein weißes Smartphone,
der weiblichen Käufer kaufen ein weißes Smartphone,  aller männlichen Smartphonekäufer ein silbernes.
Ermittle aufgrund dieser Prognose, wie hoch der Anteil weißer Smartphones an der Gesamtanzahl verkaufter Smartphones sein wird.
aller männlichen Smartphonekäufer ein silbernes.
Ermittle aufgrund dieser Prognose, wie hoch der Anteil weißer Smartphones an der Gesamtanzahl verkaufter Smartphones sein wird.
Eine Prognose des Herstellers besagt, dass dieses Modell in
(3 BE)
3.3
Die Bildschirmdiagonale des neuen Smartphonemodells beträgt 
 entspricht
entspricht 
3.3.1
Zeige, dass die Bildschirmdiagonale dieses Smartphonemodells  beträgt.
beträgt.
(2 BE)
3.3.2
Der rechteckige Bildschirm wird das Format  haben.
haben.
Ermittle die Höhe und die Breite des Bildschirms.
Ermittle die Höhe und die Breite des Bildschirms.
(2 BE)
1.1
Koordinaten des Schnittpunkts bestimmen
![\(\begin{array}[t]{rll}
f(0)&=& 3\cdot 2^0 -1 \\[5pt]
&=& 3\cdot 1 -1\\[5pt]
&=& 2
\end{array}\)](https://www.schullv.de/resources/formulas/ad5e64bf0bfd2ececc2d8162d27e38b8d350171734649d00d6fc8b5533f12d2a_light.svg) Der Graph von
Der Graph von  schneidet die
schneidet die  -Achse im Punkt
-Achse im Punkt  Wertebereich angeben
Da
Wertebereich angeben
Da  niemals negativ werden kann, sich für große negative Werte von
niemals negativ werden kann, sich für große negative Werte von  aber Null annähert, sind alle Funktionswerte von
aber Null annähert, sind alle Funktionswerte von  größer als
größer als  Für große positive Werte von
Für große positive Werte von  werden auch die Funktionswerte größer. Insgesamt ist der Wertebereich daher:
werden auch die Funktionswerte größer. Insgesamt ist der Wertebereich daher:


1.2
Mit dem solve-Befehl des CAS kann die Gleichung  gelöst werden:
gelöst werden:
![\(\begin{array}[t]{rll}
f(x)&=& 47 &\quad \scriptsize \mid\; CAS \\[5pt]
x &=& 4
\end{array}\)](https://www.schullv.de/resources/formulas/298676dfcc38a9c99c76bfcb7ad80132b6d1403cc34c135fa14808d94d3a7d7f_light.svg) Das Argument zum Funktionswert
Das Argument zum Funktionswert  ist
ist 
1.3
Die Koordinaten von  müssen die Funktionsgleichung erfüllen. Einsetzen der Koordinaten liefert:
müssen die Funktionsgleichung erfüllen. Einsetzen der Koordinaten liefert:
![\(\begin{array}[t]{rll}
-\dfrac{7}{8}&=& g(-2) \\[5pt]
-\dfrac{7}{8}&=& a\cdot 2^{-2} -1 \quad \scriptsize \mid\; +1\\[5pt]
\dfrac{1}{8} &=& a\cdot \dfrac{1}{4} \quad \scriptsize \mid\; \cdot 4 \\[5pt]
\dfrac{1}{2}&=& a
\end{array}\)](https://www.schullv.de/resources/formulas/960aa1c15d98d631d15959888e28d1737fb9e9e43f737a6fb995559621d67492_light.svg)
2.1
2.2
Da  und
und  auf dem Kreis mit dem Mittelpunkt
auf dem Kreis mit dem Mittelpunkt  liegen, gilt
liegen, gilt  und das Dreieck
und das Dreieck  ist folglich gleichschenklig.
ist folglich gleichschenklig.
Nach dem Basiswinkelsatz gilt daher auch
Weiter folgt
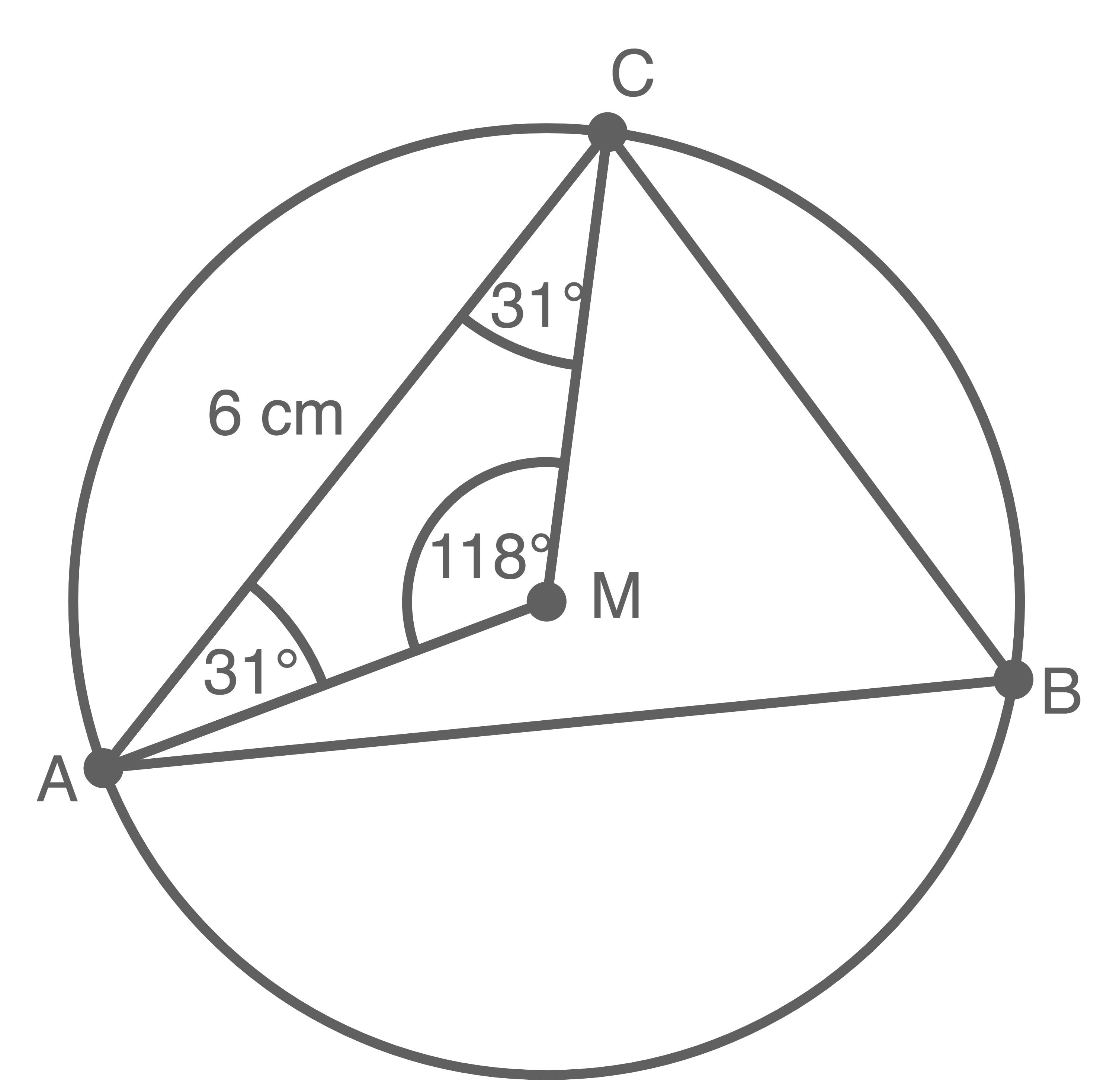 Mit dem Sinussatz gilt:
Mit dem Sinussatz gilt:
![\(\begin{array}[t]{rll}
\dfrac{\overline{AC}}{\sin \sphericalangle CMA}&=& \dfrac{\overline{MC}}{\sin \sphericalangle MAC} \\[5pt]
\dfrac{6,0\,\text{cm}}{\sin 118,0^{\circ}}&=& \dfrac{\overline{MC}}{\sin 31^{\circ}} \quad \scriptsize \mid\;\cdot \sin 31^{\circ} \\[5pt]
\dfrac{6,0\,\text{cm}}{\sin 118^{\circ}}\cdot \sin 31^{\circ}&=& \overline{MC} \\[5pt]
3,5\,\text{cm} &\approx& \overline{MC} \\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/e3e8284e48944fd9ede1f3a5eb36b8dffd8b02bc96df0a4fe7bdf9185430f4f1_light.svg)
Es gilt also Nach dem Basiswinkelsatz gilt daher auch
Weiter folgt

Skizze
2.3
1. Schritt: Flächeninhalt des Dreiecks berechnen
Verwende die alternative Formel für den Flächeninhalt eines Dreiecks. Damit erhältst du im vorliegenden Fall:
![\(\begin{array}[t]{rll}
A_D&=& \dfrac{1}{2}\cdot \overline{AB} \cdot \overline{AC} \cdot \sin \sphericalangle BAC \\[5pt]
&=& \dfrac{1}{2}\cdot 6,8\,\text{cm} \cdot 6,0\,\text{cm}\cdot \sin 43^{\circ} \\[5pt]
&=& 20,4\cdot \sin 43^{\circ}\,\text{cm}^2
\end{array}\)](https://www.schullv.de/resources/formulas/fb3f0a040d514ba41925f2ca50f764d809b5e55323abc3184784bbe1661d727f_light.svg) 2. Schritt: Flächeninhalt des Kreises berechnen
Der Radius des Umkreises beträgt
2. Schritt: Flächeninhalt des Kreises berechnen
Der Radius des Umkreises beträgt  Mit der Flächenformel eines Kreises folgt:
Mit der Flächenformel eines Kreises folgt:
![\(\begin{array}[t]{rll}
A_K&=& \pi \cdot r^2 \\[5pt]
&\approx& \pi \cdot (3,5\,\text{cm})^2 \\[5pt]
&=& 12,25\cdot \pi\,\text{cm}^2 \\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/497267addb34182a7547a3ee17b589f161ebd9e74098fdac3721f82c5a1ec87b_light.svg) 3. Schritt: Prozentualen Anteil berechnen
3. Schritt: Prozentualen Anteil berechnen
![\(\begin{array}[t]{rll}
\dfrac{A_D}{A_K}&=& \dfrac{20,4\cdot \sin 43^{\circ}\,\text{cm}^2 }{12,25\cdot \pi\,\text{cm}^2} \\[5pt]
&\approx& 0,36 \\[5pt]
&=& 36\,\% \\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/78448daaf51aababb7620222e9df00ff1b5070759adc5121aa6792ede299d9f0_light.svg) Der prozentuale Anteil des Flächeninhalts des Dreiecks
Der prozentuale Anteil des Flächeninhalts des Dreiecks  am Flächeninhalt seines Umkreises beträgt ca.
am Flächeninhalt seines Umkreises beträgt ca. 
3.1.1
Die Funktion  beschreibt die Zeit bis zum vollständigen Aufladen des Akkus in Minuten bei der Restkapazität
beschreibt die Zeit bis zum vollständigen Aufladen des Akkus in Minuten bei der Restkapazität  Für
Für  gilt:
gilt:
![\(\begin{array}[t]{rll}
t(20)&=& -0,0075\cdot 20^2 +75 \\[5pt]
&=& 72
\end{array}\)](https://www.schullv.de/resources/formulas/0877492667eb9a8749d889a0a2e9e17306a282cc02fc136f55b9234d005d74e4_light.svg) Also benötigt ein Akku des Smartphonemodells mit einer Restkapazität von
Also benötigt ein Akku des Smartphonemodells mit einer Restkapazität von  noch
noch  Minuten.
Minuten.
3.1.2
Gesucht ist  mit
mit  da die Zeit bis zum vollständigen Aufladen
da die Zeit bis zum vollständigen Aufladen  Minuten beträgt.
Mit dem solve-Befehl des CAS folgt:
Minuten beträgt.
Mit dem solve-Befehl des CAS folgt:
![\(\begin{array}[t]{rll}
t(r)&=& 30 \quad \scriptsize \mid\; CAS \\[5pt]
r&\approx& 77,5
\end{array}\)](https://www.schullv.de/resources/formulas/67aaeaddef5612dea2cb262c0762e6851338d22676d259cf8457d50d1ab2e9a7_light.svg) Ein Akku, der noch eine halbe Stunde bis zum vollständigen Aufladen benötigt, hat eine Restkapazität von ca.
Ein Akku, der noch eine halbe Stunde bis zum vollständigen Aufladen benötigt, hat eine Restkapazität von ca. 
3.1.3
Mit dem solve-Befehl des CAS folgt:
![\(\begin{array}[t]{rll}
t(r)&=& 0 \quad \scriptsize \mid\; CAS \\[5pt]
r&=& 100
\end{array}\)](https://www.schullv.de/resources/formulas/a5bb080a90cb68827afc9da76f1281a7b33ecf0dd53ef0d505df530f118cbc64_light.svg) Die Nullstelle von
Die Nullstelle von  ist
ist  Wenn der Akku also eine Restkapazität von
Wenn der Akku also eine Restkapazität von  hat, und damit voll aufgeladen ist, beträgt die Zeit bis zum vollständigen Aufladen des Akkus
hat, und damit voll aufgeladen ist, beträgt die Zeit bis zum vollständigen Aufladen des Akkus  Minuten, da der Akku bereits voll aufgeladen ist.
Minuten, da der Akku bereits voll aufgeladen ist.
3.2
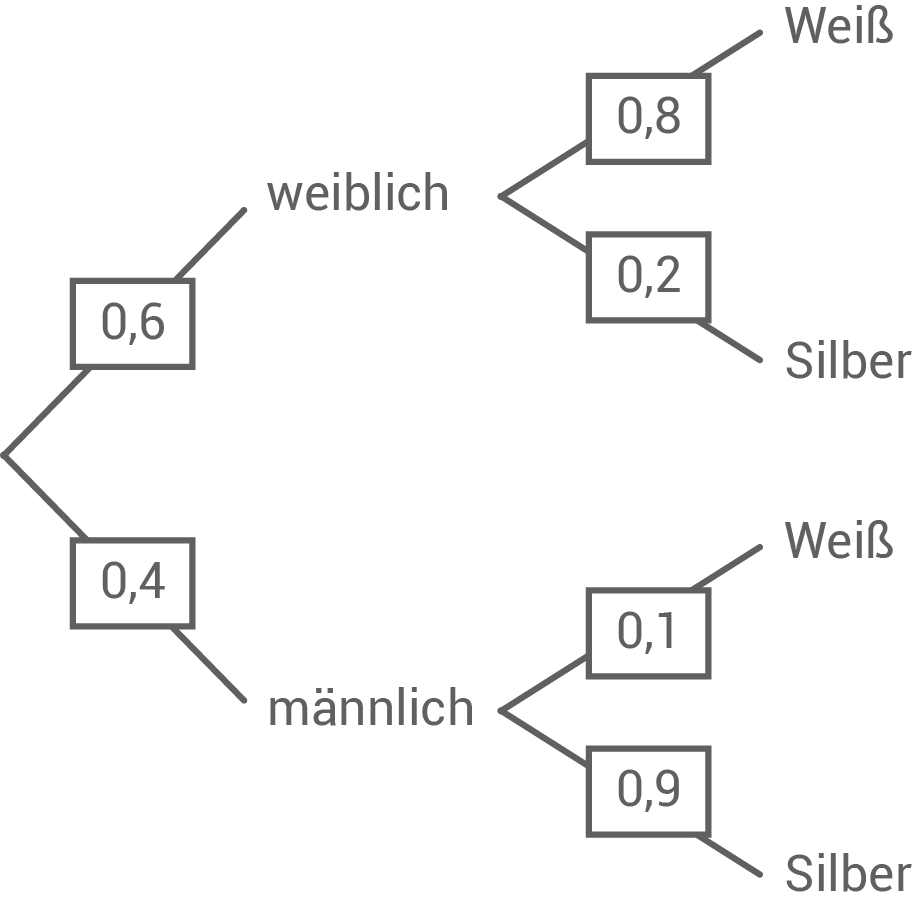
Zur Übersicht kann es hilfreich sein, ein Baumdiagramm zu zeichnen. Mit den Pfadregeln folgt:
![\(\begin{array}[t]{rll}
P(\text{Weiß})&=& 0,6\cdot 0,8 + 0,4\cdot 0,1 \\[5pt]
&=& 0,52 \\[5pt]
&=& 52\,\%
\end{array}\)](https://www.schullv.de/resources/formulas/6fafed719da31a521ca716593d92af01a8627c1fea8712965972aa579e9c7328_light.svg)
Laut Prognose beträgt der Anteil der weißen Smartphones an der Gesamtzahl aller verkauften Smartphones
3.3.1
Die Bildschrimdiagonale des Smartphones beträgt  Ein Zoll entspricht laut Aufgabenstellung
Ein Zoll entspricht laut Aufgabenstellung 
 Die Bildschirmdiagonale beträgt also
Die Bildschirmdiagonale beträgt also 
3.3.2
Das Format  gibt an, dass wenn die Breite des Bildschirms
gibt an, dass wenn die Breite des Bildschirms  beträgt, die Höhe des Bildschirms dann
beträgt, die Höhe des Bildschirms dann  beträgt. Die Bildschirmdiagonale beträgt
beträgt. Die Bildschirmdiagonale beträgt  nach Teilaufgabe 3.3.1. Aufgrund des Sachverhalts ergibt sich ein rechtwinkliges Dreieck.
nach Teilaufgabe 3.3.1. Aufgrund des Sachverhalts ergibt sich ein rechtwinkliges Dreieck.
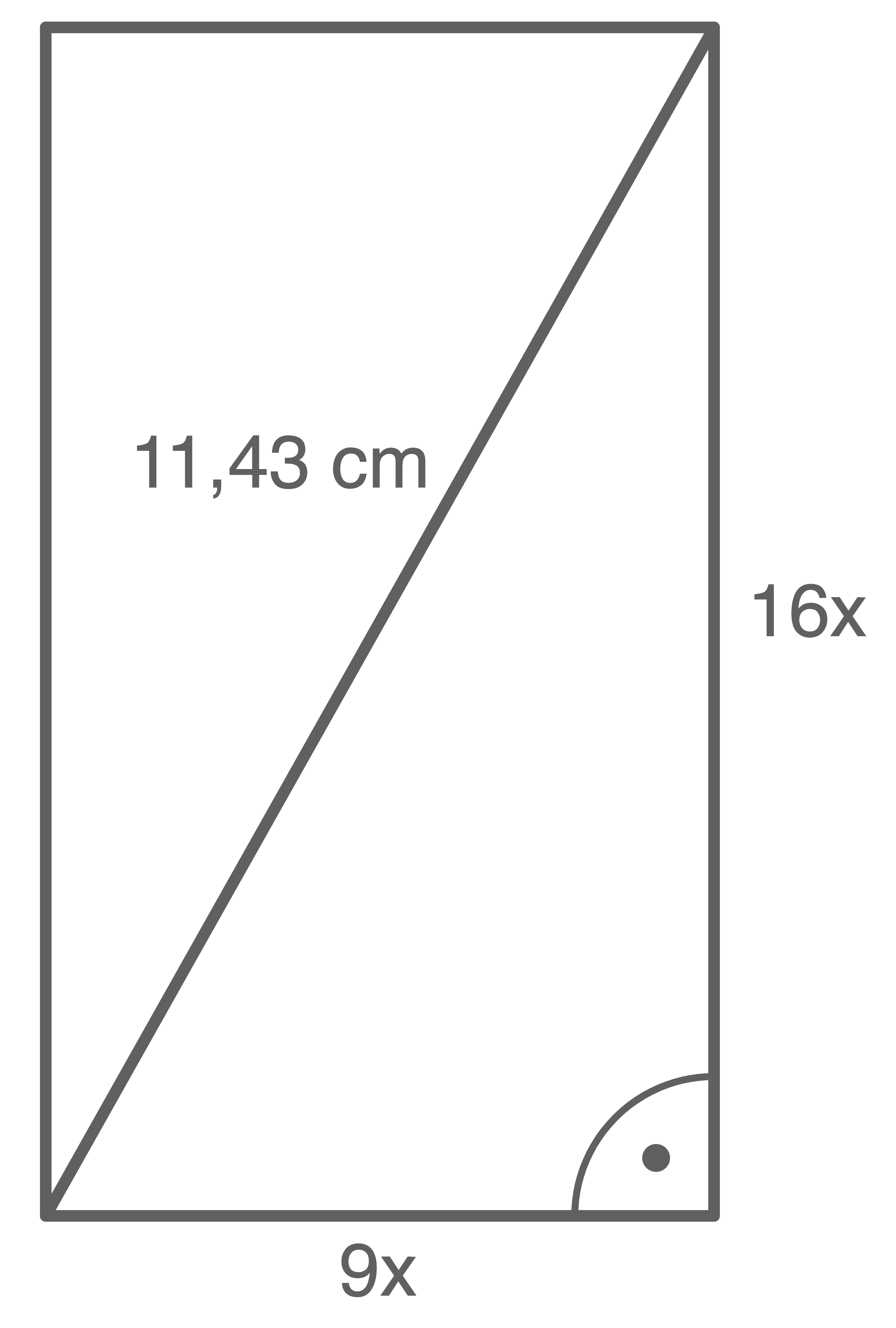
![\(\begin{array}[t]{rll}
b&=& 9x \\[5pt]
&=& 9\cdot \sqrt{\dfrac{11,43^2}{337}}\,\text{cm} \\[5pt]
&\approx& 5,6\,\text{cm} \\[10pt]
h&=& 16x \\[5pt]
&=& 16\cdot \sqrt{\dfrac{11,43^2}{337}}\,\text{cm} \\[5pt]
&\approx& 10,0\,\text{cm} \\[10pt]
\end{array}\)](https://www.schullv.de/resources/formulas/37e8f1db4da1bc4ad68658bf33dde60c38dd0c8508f591863e729e938977b372_light.svg) Die Breite des Smartphonebildschirms beträgt ca.
Die Breite des Smartphonebildschirms beträgt ca.  die Höhe ca.
die Höhe ca. 

Skizze
Mit dem Satz des Pythagoras folgt:
![\(\begin{array}[t]{rll}
(11,43\,\text{cm})^2&=& (9x)^2 +(16x)^2 \\[5pt]
11,43^2\,\text{cm}^2&=& 337x^2 \quad \scriptsize \mid\; : 337 \\[5pt]
\dfrac{11,43^2}{337}\,\text{cm}^2&=& x^2 \quad \scriptsize \mid\; \sqrt{\,} \\[5pt]
\sqrt{\dfrac{11,43^2}{337}}\,\text{cm}&=& x \\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/133dc4117f0412e11c3091aad9c90f6c8e47ed0eb00c598f2516e1b62c9c5489_light.svg)
Für die Breite und die Höhe folgt dann: