Pflichtteil 1
Aufgabe 1
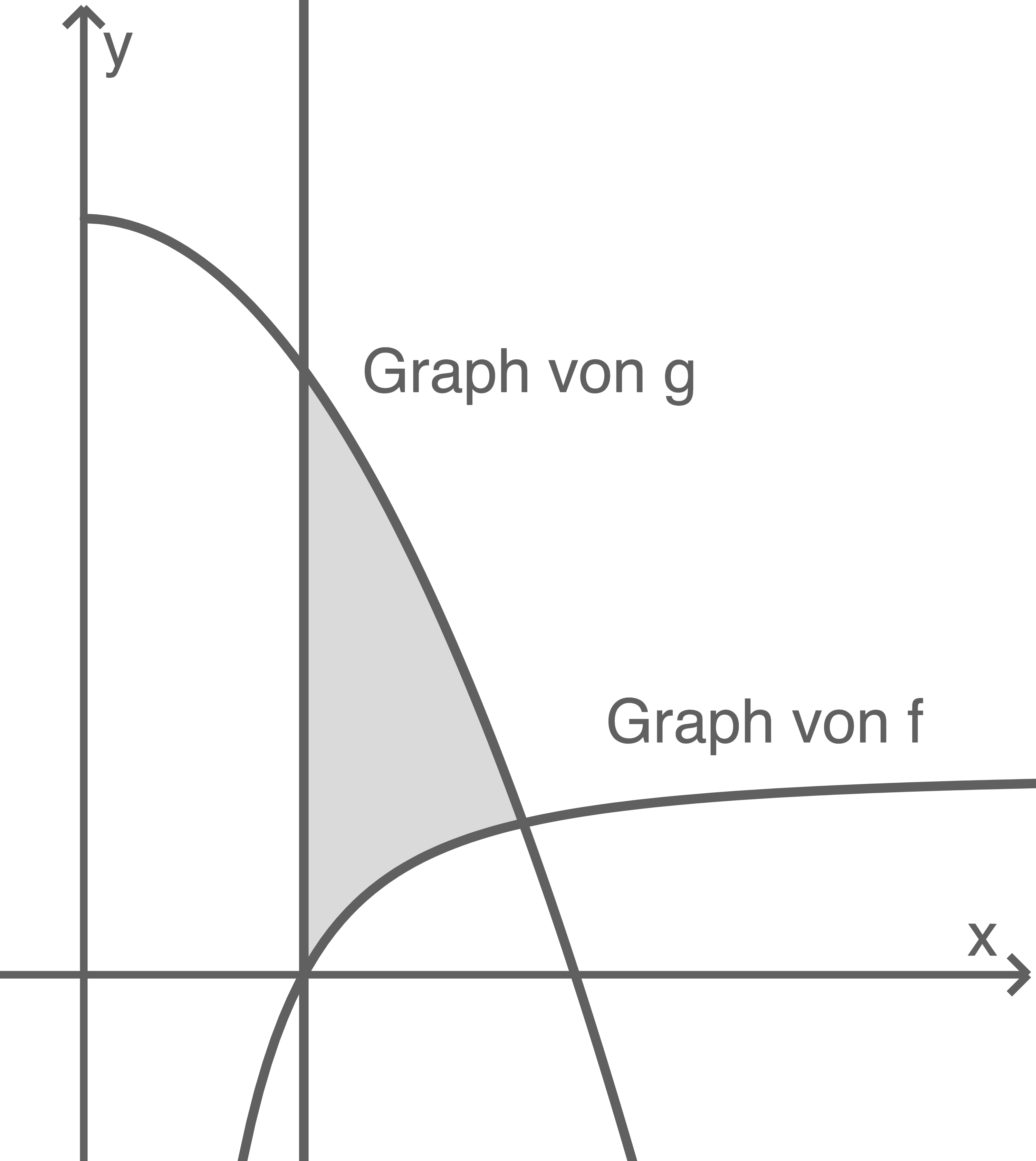
Die Abbildung zeigt die Graphen der Funktionen  mit
mit  und
und  mit
mit  , sowie die Gerade mit der Gleichung
, sowie die Gerade mit der Gleichung  .
.
a)
Zeige, dass sich die Graphen von  und
und  an der Stelle
an der Stelle  schneiden.
schneiden.
(0,5 VP)
b)
Berechne den Inhalt der markierten Fläche.
(2 VP)
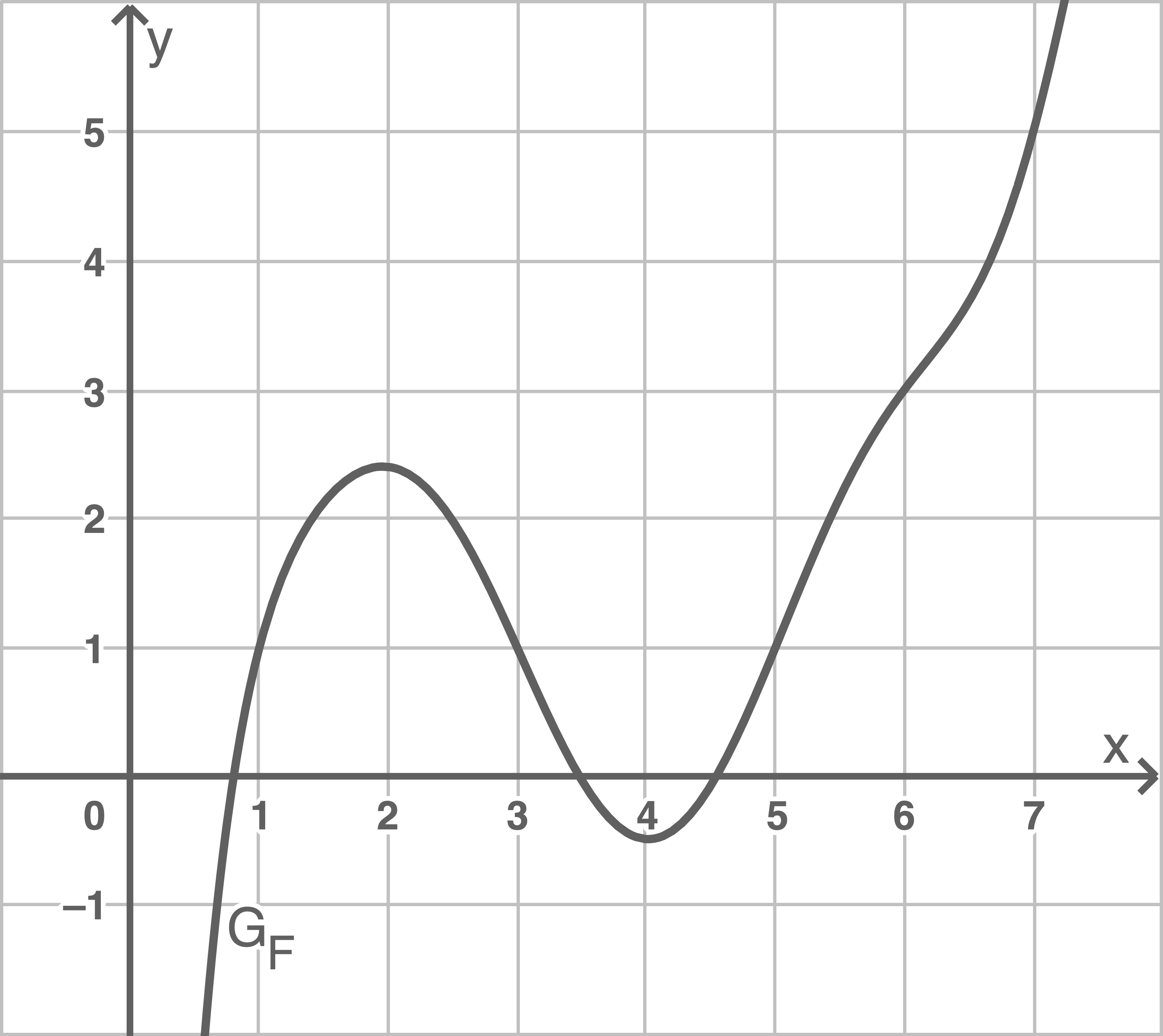
Aufgabe 2
Betrachtet werden die inDie folgende Abbildung zeigt den Graphen
a)
Bestimme den Wert des Integrals  .
.
(1 VP)
b)
Bestimme den Funktionswert von  an der Stelle
an der Stelle  . Veranschauliche dein Vorgehen in der Abbildung.
. Veranschauliche dein Vorgehen in der Abbildung.
(1,5 VP)
Aufgabe 3
Gegeben sind die in
a)
Begründe, dass der Graph von  symmetrisch bezüglich der
symmetrisch bezüglich der  -Achse ist.
-Achse ist.
(0,5 VP)
b)
Es gibt einen Wert von  , für den
, für den  eine Wendestelle von
eine Wendestelle von  ist.
ist.
Berechne diesen Wert von .
.
Berechne diesen Wert von
(2 VP)
Aufgabe 4
Ermittle eine Gleichung derjenigen quadratischen Funktion- Der Graph von
schneidet die Gerade mit der Gleichung
im Punkt
unter einem rechten Winkel.
- Die
- und
-Koordinate des Extrempunkts des Graphen von
stimmen überein.
(2,5 VP)
Aufgabe 5
Gegeben sind die Gerade
a)
Begründe, dass  orthogonal zu
orthogonal zu  ist.
ist.
(0,5 VP)
b)
Die Geraden  , hat mit
, hat mit  keinen gemeinsamen Punkt.
Es gibt Geraden, die in
keinen gemeinsamen Punkt.
Es gibt Geraden, die in  liegen und parallel zu
liegen und parallel zu  verlaufen.
verlaufen.
Bestimme eine Gleichung derjenigen dieser Graden, die von den kleinsten Abstand hat.
den kleinsten Abstand hat.
Bestimme eine Gleichung derjenigen dieser Graden, die von
(2 VP)
Aufgabe 6
Wird der Punkt
a)
Bestimme eine Gleichung von  in Koordinatenform.
in Koordinatenform.
(1,5 VP)
b)
Auf der Gerade durch  und
und  liegen die Punkte
liegen die Punkte  und
und  symmetrisch bezüglich
symmetrisch bezüglich  dabei liegt
dabei liegt  bezüglich
bezüglich  auf der gleichen Seite wie
auf der gleichen Seite wie  . Der Abstand von
. Der Abstand von  und
und  ist doppelt so groß wie der Abstand von
ist doppelt so groß wie der Abstand von  und
und  . Bestimme die Koordinaten von
. Bestimme die Koordinaten von  .
.
(1 VP)
Aufgabe 7
Die ZufallsgrößeSie hat den Erwartungswert
a)
Bestimme den Wert von  und die Standardabweichung von
und die Standardabweichung von  .
.
(1,5 VP)
b)
Entscheide, ob  ist, und begründe deine Entscheidung.
ist, und begründe deine Entscheidung.
(1 VP)
Aufgabe 8
Für ein Spiel wird ein Behälter mit 100 Kugeln gefüllt. Dafür stehen rote und blaue Kugeln zur Verfügung. Vor jedem Spiel legt der Spieler die Anzahl der blauen Kugeln im Behälter fest. Anschließend wird dem Behälter eine Kugel zufällig entnommen. Ist diese Kugel rot, so wird dem Spieler die festgelegte Anzahl blauer Kugeln in Cent ausgezahlt; ist die Kugel blau, so beträgt die Auszahlung 10 Cent. Ermittle, wie der Spieler die Anzahl blauer Kugeln für ein Spiel festlegen muss, damit der Erwartungswert der Auszahlung möglichst groß ist.
(2,5 VP)
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?Lösung 1
a)
b)
Durch die Gerade  und die Schnittstelle
und die Schnittstelle  der beiden Graphen von
der beiden Graphen von  und
und  ergeben sich die Grenzen des Integrals.
ergeben sich die Grenzen des Integrals.
Lösung 2
a)
An  können die Funktionswerte an den Stellen
können die Funktionswerte an den Stellen  und
und  abgelesen werden. Somit folgt:
abgelesen werden. Somit folgt:
![\(\begin{array}[t]{rll}
\displaystyle\int_{1}^{7}f(x)\;\mathrm dx&=& F(7)-F(1)&\ \\[5pt]
&=& 5-1&\ \\[5pt]
&=& 4 \, [\text{FE}]
\end{array}\)](https://www.schullv.de/resources/formulas/1ca12edfbae91949b0895b4a3afba7994b396a2e8d4fb3f701f3f4bdf34d86da_light.svg)
b)
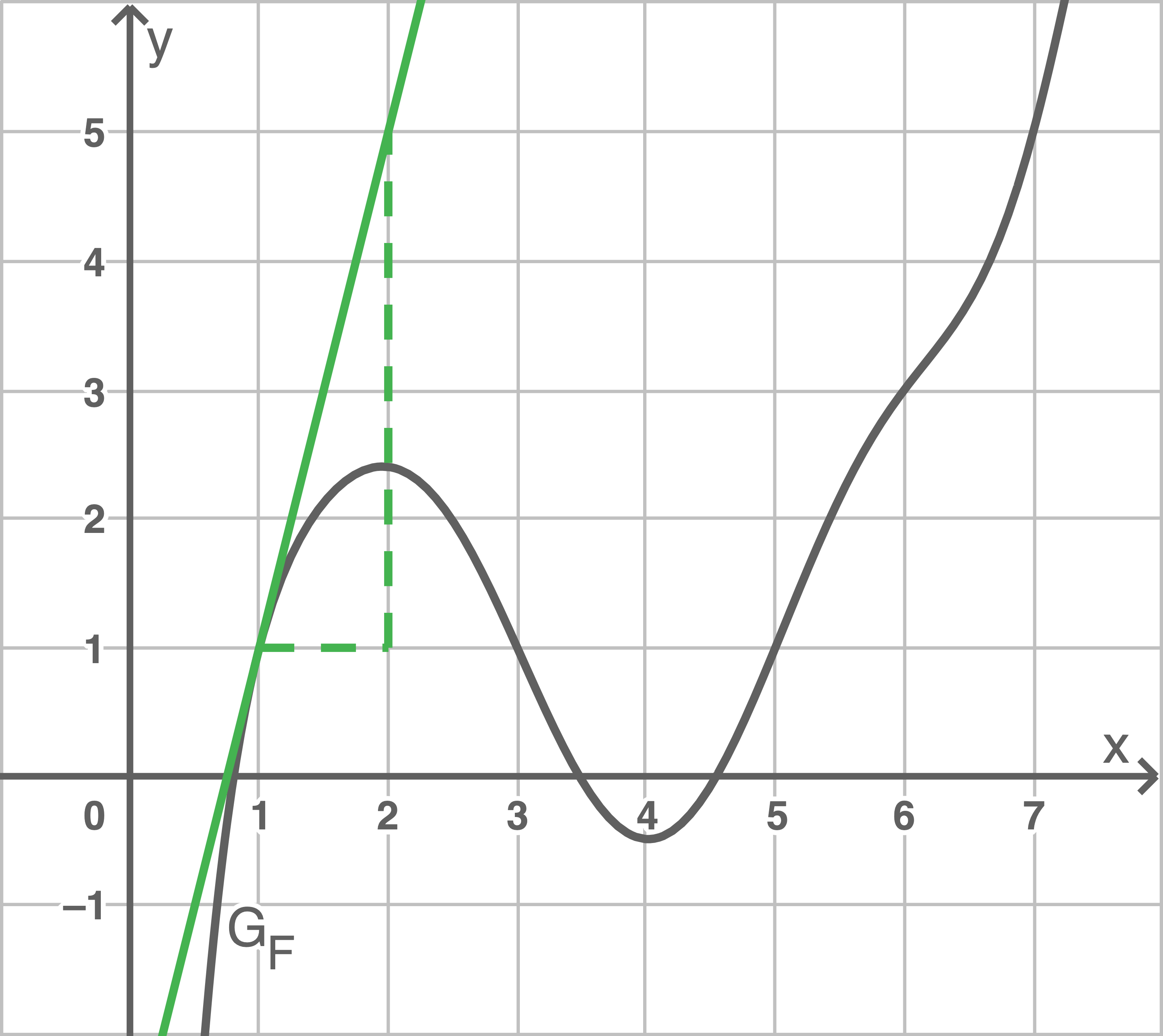
Lösung 3
a)
b)
1. Schritt: Erste und zweite Ableitung von  bilden
bilden
![\(\begin{array}[t]{rll}
f_k](https://www.schullv.de/resources/formulas/14a3526795b4a8ad54202339e37b1fb5411e5a20454582993f82dfadbbc746ea_light.svg)
![\(\begin{array}[t]{rll}
f_k](https://www.schullv.de/resources/formulas/f325a28836a02ff89261f6ef7359a8c770f522b724d9e9f311850b161acb9bba_light.svg) 2. Schritt: Notwendige Bedingung für Wendestellen anwenden
Es soll
2. Schritt: Notwendige Bedingung für Wendestellen anwenden
Es soll  an der Stelle
an der Stelle  gelten, daraus folgt:
Da vorausgesetzt ist, dass bei
gelten, daraus folgt:
Da vorausgesetzt ist, dass bei  eine Wendestelle existiert, muss die hinreichende Bedingung für Wendestellen nicht mehr geprüft werden.
eine Wendestelle existiert, muss die hinreichende Bedingung für Wendestellen nicht mehr geprüft werden.
Lösung 4
Quadratische Funktionsgleichung:Lösung 5
a)
Der Vektor  ist sowohl Richtungsvektor der Geraden
ist sowohl Richtungsvektor der Geraden  als auch ein Normalenvektor von der Ebene
als auch ein Normalenvektor von der Ebene  Deshalb ist auch
Deshalb ist auch  orthogonal zu
orthogonal zu 
b)
Da die gesuchte Gerade parallel zu  verlaufen soll, muss der Richtungsvektor identisch sein und somit:
verlaufen soll, muss der Richtungsvektor identisch sein und somit:  Um diejenige Gerade mit dem geringstem Abstand zur Geraden
Um diejenige Gerade mit dem geringstem Abstand zur Geraden  zu finden, kann der gemeinsame Stützpunkt
zu finden, kann der gemeinsame Stützpunkt  der Geraden
der Geraden  und der Hilfsgeraden
und der Hilfsgeraden  als Lotfußpunkt genutzt werden.
Koordinaten des Schnittpunkts der Hilfsgeraden
als Lotfußpunkt genutzt werden.
Koordinaten des Schnittpunkts der Hilfsgeraden  mit der Ebene
mit der Ebene  bestimmen:
bestimmen:
![\(\begin{array}[t]{rll}
3\cdot(7+3r)-(3-r)&=& -2 & \\[5pt]
21+9r-3+r&=& -2 & \\[5pt]
18+10r&=& -2 &\quad \scriptsize \mid\;-18 \\[5pt]
10r&=& -20 &\quad \scriptsize \mid\; :10\\[5pt]
r&=& -2
\end{array}\)](https://www.schullv.de/resources/formulas/a89b79546237ac6a04d2a5b7553c3a0fb8c8b913c1c331580da14222f10943e0_light.svg) Durch Einsetzen von
Durch Einsetzen von  in
in  ergibt sich:
ergibt sich:
![\(\begin{array}[t]{rll}
\overrightarrow{OX}&=& \pmatrix{7\\3\\3}-2\cdot\pmatrix{3\\0\\-1}& \\[5pt]
&=&\pmatrix{1\\3\\5}
\end{array}\)](https://www.schullv.de/resources/formulas/c689f76c919990c8418900a59ea6f3b980edafcc08bb7abcba561b46909c59da_light.svg) Eine Gleichung der gesuchten Geraden ist somit
Eine Gleichung der gesuchten Geraden ist somit  mit
mit 
Lösung 6
a)
Ein Normalenvektor von  entspricht
entspricht 
![\(\begin{array}[t]{rll}
\overrightarrow{PQ}&=& \pmatrix{7\\2\\11}-\pmatrix{1\\2\\3}&\ \\[5pt]
&=&\pmatrix{6\\0\\8}
\end{array}\)](https://www.schullv.de/resources/formulas/7e9661e46d6e585e64e6217708537dc6f3b4ac05d9aa64b099640a9f36e65630_light.svg) Ortsvektor des Mittelpunkts
Ortsvektor des Mittelpunkts  der Strecke
der Strecke  :
:
![\(\begin{array}[t]{rll}
\overrightarrow{OM}&=&\pmatrix{1\\2\\3}+\dfrac{1}{2}\cdot\pmatrix{6\\0\\8}& \\[5pt]
&=&\pmatrix{4\\2\\7}
\end{array}\)](https://www.schullv.de/resources/formulas/81c5c7a7d8db76d3ae9cf17d96c27145cb83bc3452396d9e75890237e757c611_light.svg) Aus
Aus  und den Koordinaten von
und den Koordinaten von  ergibt sich folgende Koordinatenform für die gesuchte Ebene
ergibt sich folgende Koordinatenform für die gesuchte Ebene  :
:
![\(\begin{array}[t]{rll}
E: 6x_1+0x_2+8x_3&=& c& \\[5pt]
6\cdot4+0\cdot2+8\cdot7&=& c & \\[5pt]
80&=& c & \\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/c401e435075d8fbe88c3d9662f61be96f640dcd24ac0e6ffcffc137e8415c3ae_light.svg)
![\(\begin{array}[t]{rll}
E: 6x_1+0x_2+8x_3&=& 80&\quad \scriptsize \mid\;:2 \\[5pt]
3x_1+4x_3&=& 40
\end{array}\)](https://www.schullv.de/resources/formulas/ecfcf9aab87c60635e152ba31e9cbce67fd7f19868eabf38f4228de6c4ae1bd8_light.svg)
b)
Da  gelten soll, folgt:
gelten soll, folgt:  Koordinaten von
Koordinaten von  :
:
![\(\begin{array}[t]{rll}
\overrightarrow{OR}&=& \overrightarrow{OM}+2\cdot\overrightarrow{MP}&\ \\[5pt]
&=& \pmatrix{4\\2\\7}+2\cdot\pmatrix{-3\\0\\-4}&\ \\[5pt]
&=&\pmatrix{-2\\2\\-1}
\end{array}\)](https://www.schullv.de/resources/formulas/3e5699bf1eab4c2d19ccc68fe34f70a4ef2f9e7ecc90a0b65dbf0394fca0f145_light.svg)

Lösung 7
a)
Wert von 
 liefert:
liefert:
![\(\begin{array}[t]{rll}
n\cdot0,5&=& 18&\quad \scriptsize \mid\;\cdot2\\[5pt]
n&=&36
\end{array}\)](https://www.schullv.de/resources/formulas/e069891bde275c58f3349e479261546b5b8e0d86fb770f27849c45bcdd902885_light.svg) Standardabweichung
Standardabweichung  :
:
![\(\begin{array}[t]{rll}
\sigma&=& \sqrt{n\cdot p\cdot(1-p)}& \\[5pt]
&=& \sqrt{36\cdot 0,5\cdot(1-0,5)}& \\[5pt]
&=& \sqrt{9}& \\[5pt]
&=& 3
\end{array}\)](https://www.schullv.de/resources/formulas/8587fdbb70198be0e1ef71aa73f9bae199468f0d89b59b4c10b04d5570113616_light.svg)
b)
Die Aussage ist falsch!
Wegen  entsteht eine symmetrische Verteilung um den Erwartungswert. Außerdem gilt
entsteht eine symmetrische Verteilung um den Erwartungswert. Außerdem gilt  und
und  , woraus
, woraus  folgt.
folgt.