Wahlteil A1
Aufgabe A1.1
Die Abbildung zeigt den Graphen einer Funktion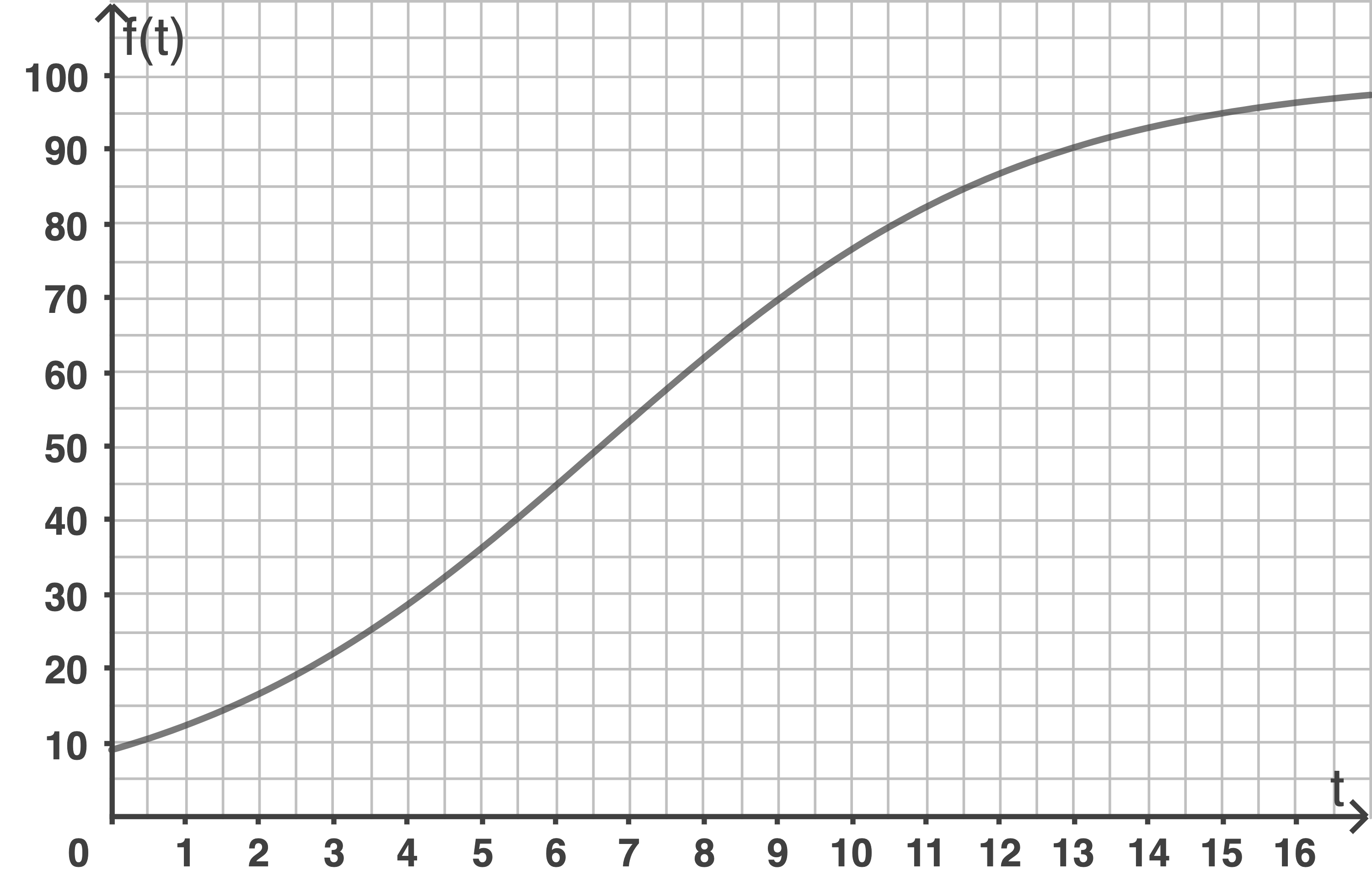
a)
Gib den Zeitraum an, in dem die Höhe der Pflanze von  auf
auf  zunimmt.
zunimmt.
Bestimme die momentane Änderungsrate der Pflanzenhöhe Wochen nach Beobachtungsbeginn.
Wochen nach Beobachtungsbeginn.
Die Funktion hat bei
hat bei  eine Wendestelle.
eine Wendestelle.
Beschreibe die Bedeutung dieser Wendestelle im Sachzusammenhang.
Bestimme die momentane Änderungsrate der Pflanzenhöhe
Die Funktion
Beschreibe die Bedeutung dieser Wendestelle im Sachzusammenhang.
(4 VP)
b)
Formuliere zu der Gleichung  eine Fragestellung im Sachzusammenhang.
eine Fragestellung im Sachzusammenhang.
Gib eine Lösung der Gleichung an.
Gib eine Lösung der Gleichung an.
(2,5 VP)
Aufgabe A1.2
Gegeben ist die FunktionDie Abbildung zeigt ihren Graphen.
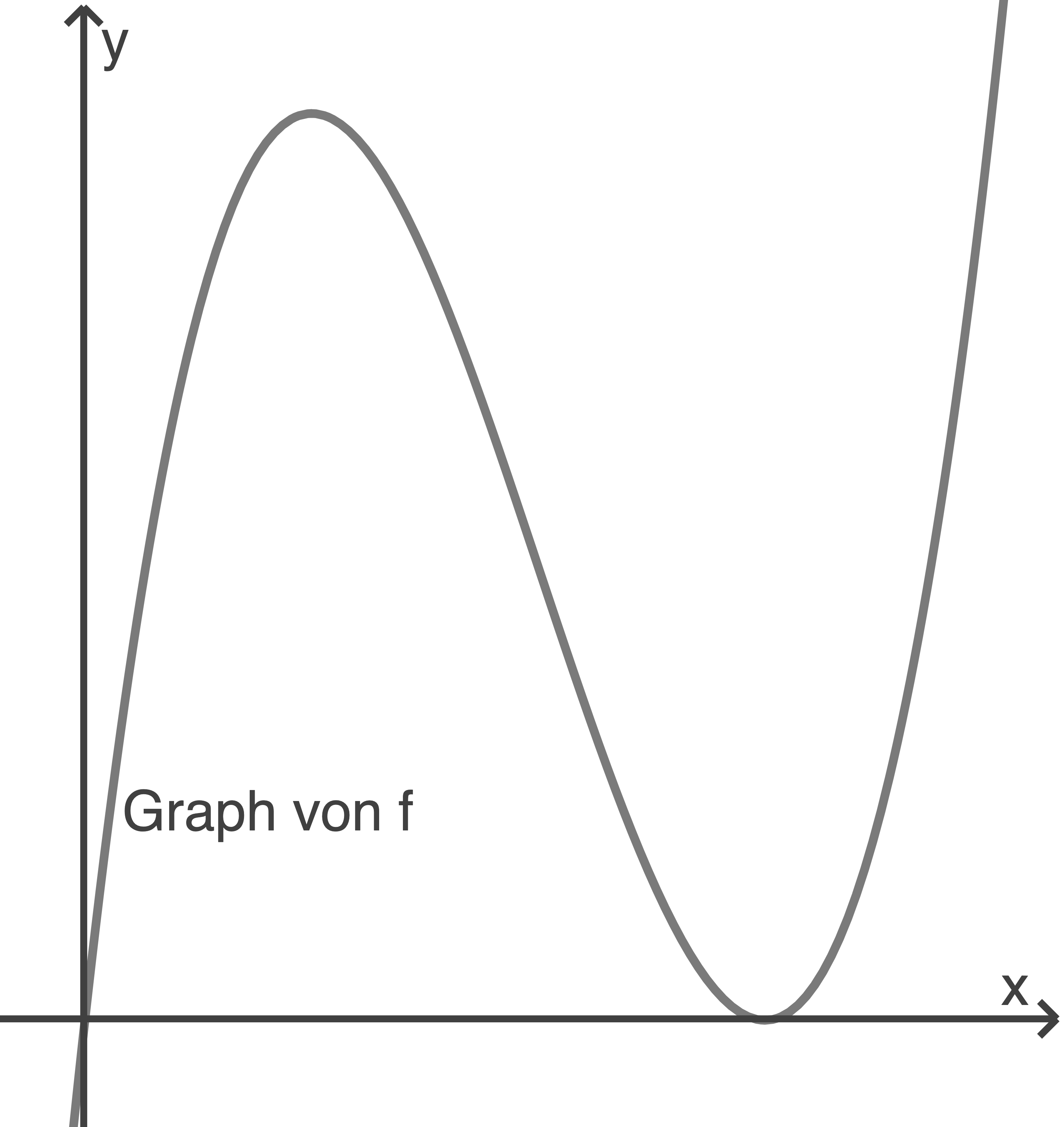
a)
Weise nach, dass der Punkt  Tiefpunkt des Graphen von
Tiefpunkt des Graphen von  ist.
ist.
Betrachtet wird die Strecke zwischen
zwischen  und dem Hochpunkt
und dem Hochpunkt  des Graphen von
des Graphen von  . Diese Strecke und der Graph von
. Diese Strecke und der Graph von  begrenzen eine Fläche.
begrenzen eine Fläche.
Berechne deren Inhalt.
Betrachtet wird die Strecke
Berechne deren Inhalt.
(5 VP)
b)
Die Funktion  ist gegeben durch
ist gegeben durch  .
.
Beschreibe, wie der Graph von aus dem Graphen von
aus dem Graphen von  entsteht.
entsteht.
Bestimme damit die Koordinaten des Tiefpunktes des Graphen von .
.
Beschreibe, wie der Graph von
Bestimme damit die Koordinaten des Tiefpunktes des Graphen von
(3 VP)
c)
Ein Kreis, dessen Mittelpunkt  auf der Geraden mit der Gleichung
auf der Geraden mit der Gleichung  liegt, berührt den Graphen von
liegt, berührt den Graphen von  im Punkt
im Punkt  .
.
Berechne die Koordinaten von .
.
Berechne die Koordinaten von
(2,5 VP)
d)
Für jedes  mit
mit  ist eine Funktion
ist eine Funktion  gegeben durch
gegeben durch
 Berechne die Werte von
Berechne die Werte von  , für die die Tangente an den Graphen von
, für die die Tangente an den Graphen von  im Punkt
im Punkt  parallel zur Geraden mit der Gleichung
parallel zur Geraden mit der Gleichung  ist.
ist.
(3 VP)
Aufgabe A1.1
a)
Zeitraum angeben
Der Abbildung lässt sich entnehmen:  und
und 
Im Zeitraum zwischen und
und  Wochen nach Beobachtungsbeginn nimmt die Höhe der Pflanze von
Wochen nach Beobachtungsbeginn nimmt die Höhe der Pflanze von  auf
auf  zu.
Momentane Änderungsrate bestimmen
In die Abbildung wird die Tangente an den Graphen an der Stelle
zu.
Momentane Änderungsrate bestimmen
In die Abbildung wird die Tangente an den Graphen an der Stelle  eingezeichnet. Mithilfe eine Steigungsdreiecks mit den Eckpunkten
eingezeichnet. Mithilfe eine Steigungsdreiecks mit den Eckpunkten  und (
und ( ) erhält man:
) erhält man:

 Wochen nach Beobachtungsbeginn, beträgt die momentane Änderungsrate ca.
Wochen nach Beobachtungsbeginn, beträgt die momentane Änderungsrate ca.  pro Woche.
Bedeutung der Wendestelle im Sachzusammenhang beschreiben
Die Wachstumsgeschwindigkeit ist an der Wendestelle von
pro Woche.
Bedeutung der Wendestelle im Sachzusammenhang beschreiben
Die Wachstumsgeschwindigkeit ist an der Wendestelle von  maximal. D.h. hier wächst die Pflanze am schnellsten.
maximal. D.h. hier wächst die Pflanze am schnellsten.
Im Zeitraum zwischen
b)
Fragestellung im Sachzusammenhang formulieren
 "In welchem Zeitraum mit der Länge von zwei Wochen, nimmt die Höhe der Pflanze um 5 cm zu?"
Lösung der Gleichung angeben
Der Abbildung lässt sich entnehmen:
"In welchem Zeitraum mit der Länge von zwei Wochen, nimmt die Höhe der Pflanze um 5 cm zu?"
Lösung der Gleichung angeben
Der Abbildung lässt sich entnehmen:  und
und 
Eine mögliche Lösung ist also
Eine mögliche Lösung ist also
Aufgabe A1.2
a)
Tiefpunkt nachweisen
1. Schritt: Ableitungsfunktionen aufstellen
![\(\begin{array}[t]{rll}
f(x)&= \dfrac{1}{4}x^3 -3x^2 +9x \\[5pt]
f](https://www.schullv.de/resources/formulas/6cf52a0e221e38a29ce2830b4228fcce6a6c39eedc7db5a546624682beede446_light.svg) 2. Schritt: Notwendiges Kriterium überprüfen
2. Schritt: Notwendiges Kriterium überprüfen
![\(\begin{array}[t]{rll}
f](https://www.schullv.de/resources/formulas/56a141a0d45d5d33e78fd5908c406607d5f857d10aac387bcdbbbc87c62dcb74_light.svg) Das notwendige Kriterium für Extremstellen von
Das notwendige Kriterium für Extremstellen von  ist an der Stelle
ist an der Stelle  also erfüllt.
3. Schritt: Hinreichendes Kriterium überprüfen
also erfüllt.
3. Schritt: Hinreichendes Kriterium überprüfen
![\(\begin{array}[t]{rll}
f](https://www.schullv.de/resources/formulas/d69c215f8509e13c94c659a591c4a7deae7346263154dd36582a4378b7c4262f_light.svg) Da das hinreichende Kriterium
Da das hinreichende Kriterium  für Minimalstellen erfüllt ist und das notwendige Kriterium für Extremstellen ebenfalls erfüllt ist, besitzt der Graph von
für Minimalstellen erfüllt ist und das notwendige Kriterium für Extremstellen ebenfalls erfüllt ist, besitzt der Graph von  an der Stelle
an der Stelle  einen Tiefpunkt.
Zudem gilt:
einen Tiefpunkt.
Zudem gilt:

 Damit ist nachgewiesen, dass
Damit ist nachgewiesen, dass  Tiefpunkt des Graphen von
Tiefpunkt des Graphen von  ist.
Flächeninhalt berechnen
1. Schritt: Geradengleichung durch
ist.
Flächeninhalt berechnen
1. Schritt: Geradengleichung durch  und
und  bestimmen
bestimmen

 2. Schritt: Flächeninhalt berechnen
Der Flächeninhalt zwischen zwei Graphen kann mit einem Integral berechnet werden:
Der Flächeninhalt der vom Graphen von
2. Schritt: Flächeninhalt berechnen
Der Flächeninhalt zwischen zwei Graphen kann mit einem Integral berechnet werden:
Der Flächeninhalt der vom Graphen von  und der Strecke durch
und der Strecke durch  und
und  eingeschlossenen Fläche beträgt
eingeschlossenen Fläche beträgt 
b)
Zusammenhang der Graphen beschreiben
 geht also durch Spiegelung an der
geht also durch Spiegelung an der  -Achse und Streckung in
-Achse und Streckung in  -Richtung mit dem Faktor
-Richtung mit dem Faktor  und anschließender Verschiebung um
und anschließender Verschiebung um  Einheiten in negativer
Einheiten in negativer  -Richtung hervor.
Koordinaten des Tiefpunkts bestimmen
Aufgrund der Spiegelung an der
-Richtung hervor.
Koordinaten des Tiefpunkts bestimmen
Aufgrund der Spiegelung an der  -Achse werden Maximalstellen von
-Achse werden Maximalstellen von  zu Minimalstellen von
zu Minimalstellen von  und umgekehrt. Die
und umgekehrt. Die  -Koordinate des Tiefpunkts des Graphen von
-Koordinate des Tiefpunkts des Graphen von  ist also
ist also 

 Die Koordinaten des Tiefpunkts des Graphen von
Die Koordinaten des Tiefpunkts des Graphen von  lauten
lauten 
- Durch den Faktor
wird der Graph von
im Vergleich zum Graphen von
um den Faktor
in
-Richtung gestreckt und durch das negative Vorzeichen an der
-Achse gespiegelt.
- Durch den Summanden
wird der Graph anschließend in negative
-Richtung um
Einheiten verschoben.
c)
Koordinaten berechnen
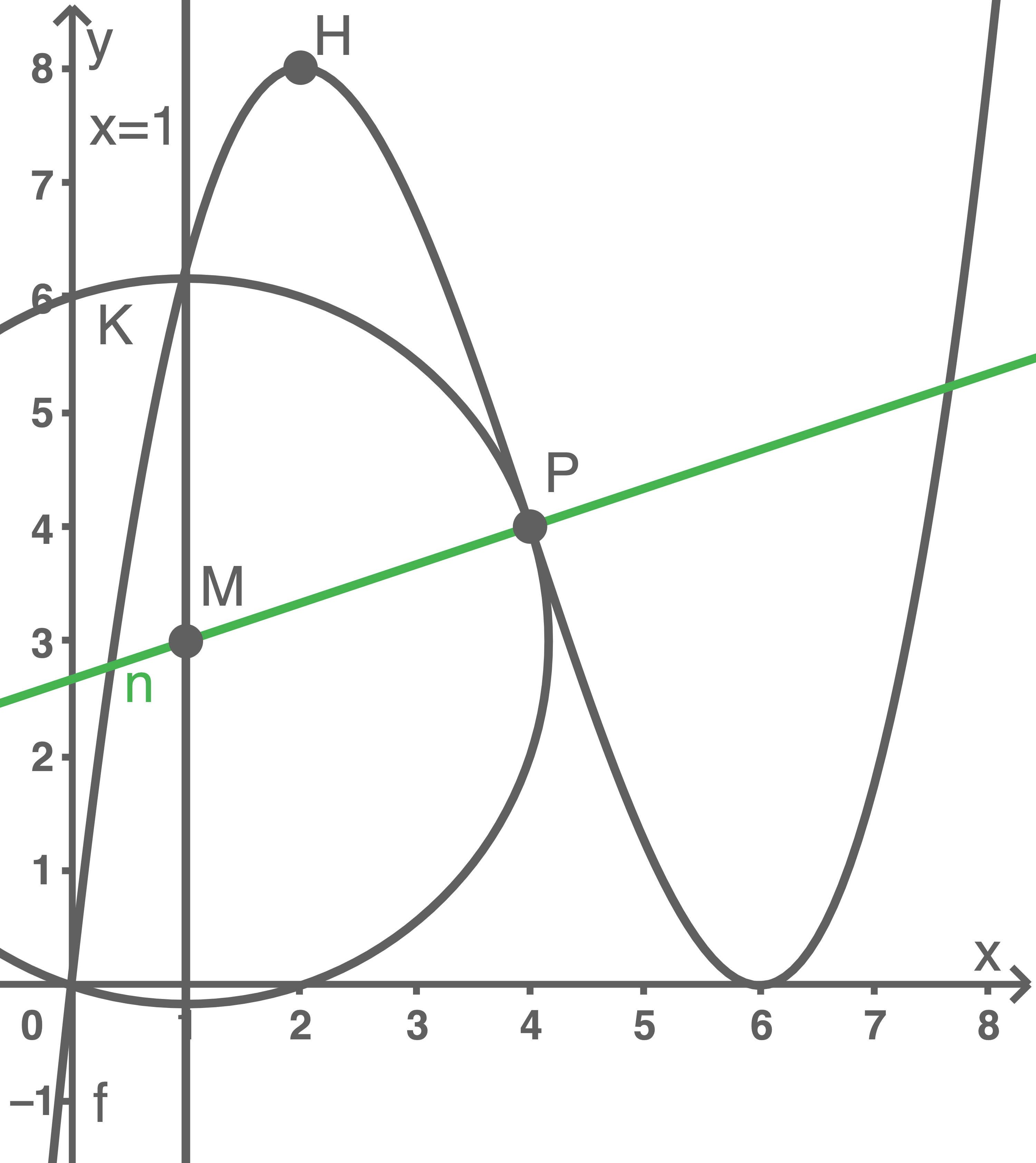
Es ist  da der Mittelpunkt
da der Mittelpunkt  von
von  auf der Geraden
auf der Geraden  liegt.
Die Steigung der Geraden
liegt.
Die Steigung der Geraden  ist gleich der Steigung der Normalen in
ist gleich der Steigung der Normalen in 
![\(\begin{array}[t]{rll}
\dfrac{4-y_M}{4-1}&=&\dfrac{1}{3} \\[5pt]
4-y_M&=&1\\
3&=&y_M
\end{array}\)](https://www.schullv.de/resources/formulas/e5e56418641b6e5813a154b58e73570bbcb1a6a58d76456b9584f2a72cb7dc1a_light.svg)

d)
Parameterwerte berechnen
Gesucht sind die Werte von  für die
für die  ist.
ist.


![\(\begin{array}[t]{rll}
f_k](https://www.schullv.de/resources/formulas/9ea0f8c7b3ec90ef7cbe956cc9ee32e8168c4582a3afff64de06d8f7c1060e93_light.svg)
![\(\begin{array}[t]{rll}
k_{1/2} &=& -\dfrac{- \frac{28}{9}}{2}\pm \sqrt{\left(\dfrac{- \frac{28}{9}}{2} \right)^2 -\dfrac{1}{3} } \\[5pt]
&=& \dfrac{14}{9}\pm \dfrac{13}{9}\\[10pt]
k_1 &=& \dfrac{14}{9}- \dfrac{13}{9} \\[5pt]
&=& \dfrac{1}{9} \\[10pt]
k_2 &=& \dfrac{14}{9}+ \dfrac{13}{9} \\[5pt]
&=& 3
\end{array}\)](https://www.schullv.de/resources/formulas/b26e84e852618d60361cc4f965ae5246edbf35c66c3a0b20607c2fd975fdfed1_light.svg) Für
Für  und
und  verläuft die Tangente an den Graphen von
verläuft die Tangente an den Graphen von  im Punkt
im Punkt  parallel zur Geraden mit der Gleichung
parallel zur Geraden mit der Gleichung 