Wahlteil A2

Aufgabe A2.1

In einem Labor wird erforscht, wie sich Bakterien unter verschiedenen Bedingungen entwickeln. Betrachtet wird jeweils der Flächeninhalt der von den Bakterien eingenommenen Fläche.

Versuchsreihe 1

Bei ungehinderter Vermehrung wird der Flächeninhalt während der ersten zwölf Stunden beschrieben durch die Funktion $f$ mit

$f(t)=20\cdot \mathrm e^{0,1\cdot t}$ ( $t$ in Stunden nach Beobachtungsbeginn, $f(t)$ in $\text {mm}^2).$

Bestimme den Flächeninhalt drei Stunden nach Beobachtungsbeginn.
Berechne den Zeitpunkt, zu dem sich der Flächeninhalt im Vergleich zum Beobachtungsbeginn verdreifacht hat.
Berechne die momentane Änderungsrate des Flächeninhalts zwei Stunden nach dem Beobachtungsbeginn.

(3,5 VP)

Berechne $\dfrac{1}{4}\cdot \displaystyle\int_{5}^{9}f(t)\;\mathrm dt.$

Interpretiere das Ergebnis im Sachzusammenhang.

(3,5 VP)

Versuchsreihe 2

Wenn man einer Bakterienkultur ein Antibiotikum hinzugibt, dann wird der Flächeninhalt durch die Funktion $g$ beschrieben mit

$g(t)=20\cdot \mathrm e^{0,1\cdot t-0,005\cdot t^2}$

( $t$ in Stunden nach Beobachtungsbeginn, $g(t)$ in $\text {mm}^2)$ .

Die Abbildung zeigt den Graphen der Funktion $g$ .

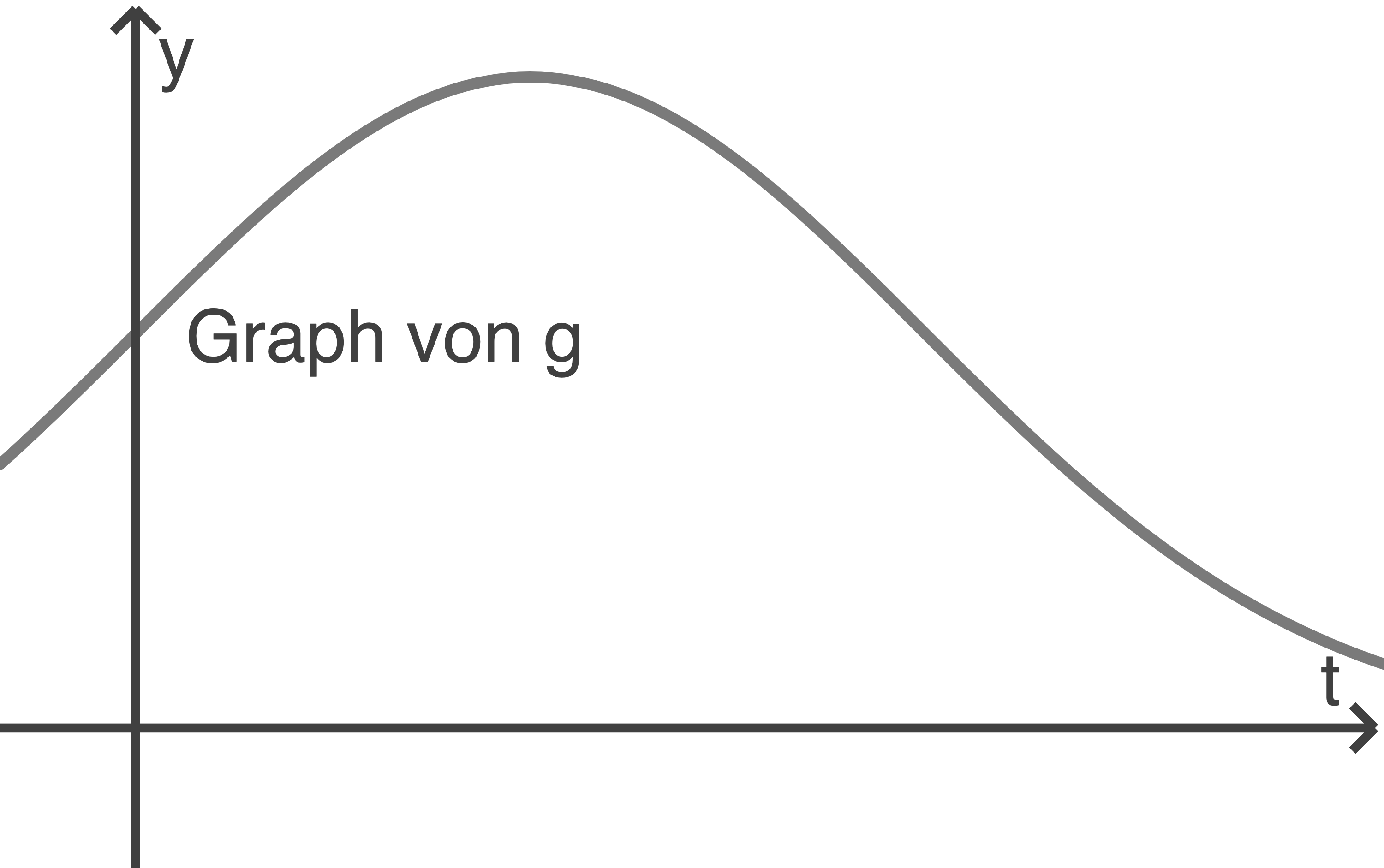
Graph der Funktion g auf einem Koordinatensystem mit Achsenbeschriftung.

Der Flächeninhalt nimmt zu einem bestimmten Zeitpunkt seinen größten Wert an.
Berechne diesen Wert.
Berechne den Zeitpunkt, zu dem der Flächeninhalt wieder so groß ist wie zu Beobachtungsbeginn.

(5 VP)

Betrachtet wird die Funktion $h$ mit $h(t)=g(t+10)$ .
Für jede reelle Zahl $t$ gilt: $h(-t)=h(t)$ .
Erläutere, welche geometrische Eigenschaft des Graphen von $g$ damit begründet werden kann.

(2 VP)

Aufgabe A2.2

Für jedes $t\gt 0$ ist eine Funktion $f_t$ gegeben durch $f_t(x)=x^4-2tx^2+8t$ .
Der Graph der Funktion $f_t$ ist $G_t$ .

Bestimme $t$ so, dass der Punkt $P(1\mid 4)$ auf dem Graphen $G_t$ liegt.

(1 VP)

Jeder Graph $G_t$ hat an der Stelle $x=\sqrt{t}$ einen Tiefpunkt.
Berechne denjenigen Wert von $t$ , für den dieser Tiefpunkt möglichst hoch liegt.

(2,5 VP)

Zeige, dass es genau zwei Punkte gibt, durch die sämtliche Graphen $G_t$ verlaufen.

(2,5 VP)

Flächeninhalt bestimmen

$\begin{array}[t]{rll} f(3) &=& 20\cdot \mathrm e^{0,1\cdot 3} \\[5pt] &=& 20\cdot \mathrm e^{0,3} \\[5pt] &\approx& 27,00 \end{array}$

Nach drei Stunden beträgt der Flächeninhalt ca. $27,00\,\text{mm}^2.$

Zeitpunkt berechnen

$\begin{array}[t]{rll} f(0)&=& 20\cdot \mathrm e^{0,1\cdot 0} \\[5pt] &=& 20 \end{array}$

Es ist $t$ gesucht mit $f(t) = 3\cdot f(0)\,$ $= 3\cdot 20 = 60.$

$\begin{array}[t]{rll} f(t) &=& 60 \\[5pt] 20\cdot \mathrm e^{0,1t} &=& 60 &\quad \scriptsize \mid\; :20 \\[5pt] \mathrm e^{0,1t} &=& 3 &\quad \scriptsize \mid\; \ln \\[5pt] 0,1t &=& \ln 3 &\quad \scriptsize \mid\; :0,1 \\[5pt] t &\approx& 10,99 \end{array}$

Ca. $11$ Stunden nach Beobachtungsbeginn hat sich der Flächeninhalt verdreifacht.

Momentane Änderungsrate berechnen

Die momentane Änderungsrate des Flächeninhalts wird durch $\(f$ beschrieben:

$\(\begin{array}[t]{rll} f(t) &=& 20\cdot \mathrm e^{0,1\cdot t} \\[10pt] f$

Zwei Stunden nach Beobachtungsbeginn beträgt die momentane Änderungsrate des Flächeninhalts ca. $2,44\,\text{mm}^2$ pro Stunde.

Integral berechnen

$\dfrac{1}{4}\cdot \displaystyle\int_{5}^{9} f(t) \;\mathrm dt$

$\begin{array}[t]{rll} &=&\dfrac{1}{4}\cdot \displaystyle\int_{5}^{9} 20\cdot \mathrm e^{0,1\cdot t}\;\mathrm dt \\[5pt] &=& \dfrac{1}{4}\cdot \left[20\cdot \dfrac{1}{0,1} \mathrm e^{0,1\cdot t}\right]_5^9 \\[5pt] &=& \dfrac{1}{4}\cdot \left[200\cdot \mathrm e^{0,1\cdot t}\right]_5^9 \\[5pt] &=& \dfrac{1}{4}\cdot \left(200\cdot \mathrm e^{0,1\cdot 9} - 200\cdot \mathrm e^{0,1\cdot 5} \right)\\[5pt] &=& \dfrac{1}{4}\cdot \left(200\cdot \mathrm e^{0,9} - 200\cdot \mathrm e^{0,5} \right) \\[5pt] &=& 50\cdot \left( \mathrm e^{0,9} -\mathrm e^{0,5} \right) \\[5pt] &\approx& 40,54 \end{array}$

Ergebnis im Sachzusammenhang interpretieren

Mit der obigen Rechnung wird der durchschnittliche Funktionswert von $f$ im Intervall $[5;9]$ berechnet.
Im Zeitraum zwischen $5$ und $9$ Stunden nach Beobachtungsbeginn beträgt der durchschnittliche Flächeninhalt ca. $40,54\,\text{mm}^2.$

Größten Wert des Flächeninhalts berechnen

1. Schritt: Ableitungsfunktion bilden

$\(\begin{array}[t]{rll} g(t)&=& 20\cdot \mathrm e^{0,1\cdot t -0,005\cdot t^2} \\[5pt] g$

2. Schritt: Notwendiges Kriterium für Extremstellen anwenden

Vollständigen Rechenweg anzeigen

$t=10$

Dies ist die einzige Nullstelle von $\(g$ Da in der Aufgabenstellung angegeben ist, dass der Flächeninhalt an einem bestimmten Zeitpunkt seinen größten Wert annimmt, muss $t=10$ die Maximalstelle sein.

3. Schritt: Funktionswert berechnen

$\begin{array}[t]{rll} g(10) &=& 20\cdot \mathrm e^{0,1\cdot 10 -0,005\cdot 10^2} \\[5pt] &=& 20\cdot \mathrm e^{0,5} \\[5pt] &\approx& 32,97 \end{array}$

Der maximale Flächeninhalt beträgt ca. $32,97\,\text{mm}^2.$

Zeitpunkt berechnen

$\begin{array}[t]{rll} g(t) &=& g(0) \\[5pt] 20\cdot \mathrm e^{0,1\cdot t -0,005\cdot t^2} &=& 20\cdot \mathrm e^{0,1\cdot 0 -0,005\cdot 0^2} \\[5pt] 20\cdot \mathrm e^{0,1\cdot t -0,005\cdot t^2} &=& 20 \quad \scriptsize \mid\; :20 \\[5pt] \mathrm e^{0,1\cdot t -0,005\cdot t^2} &=& 1 \quad \scriptsize \mid\; \ln \\[5pt] 0,1\cdot t -0,005\cdot t^2 &=& 0 \\[5pt] t\cdot \left(0,1-0,005t \right) &=& 0 \quad \scriptsize \mid\; t_1 = 0\\[5pt] 0,1-0,005t &=& 0 \quad \scriptsize \mid\;-0,1\\[5pt] -0,005t &=& -0,1 \quad \scriptsize \mid\;:(-0,005)\\[5pt] t_2 &=& 20 \end{array}$

Nach $20$ Stunden ist der Flächeninhalt wieder so groß wie zu Beobachtungsbeginn.

Geometrische Eigenschaft begründen

Für jede reelle Zahl $t$ gilt: $h(-t) = h(t).$ Daher ist der Graph von $h$ achsensymmetrisch zur $y$ -Achse.

Der Graph von $g$ geht durch Verschiebung um $10$ Einheiten in positive $t$ -Richtung aus dem Graphen von $h$ hervor. Der Graph von $g$ ist also achsensymmetrisch zur Geraden mit der Gleichung $t=10.$

Aufgabe A2.2

Parameterwert bestimmen

$\begin{array}[t]{rll} f_t(1) &=& 4\\[5pt] 1^4 -2\cdot t\cdot 1^2 + 8\cdot t &=& 4\\[5pt] 1 -2\cdot t + 8t &=& 4\\[5pt] 1 +6\cdot t &=& 4 \quad \scriptsize \mid\; -1\\[5pt] 6\cdot t &=& 3 \quad \scriptsize \mid\;:6\\[5pt] t &=& 0,5 \end{array}$

Für $t=0,5$ liegt der Punkt $P(1\mid 4)$ auf dem Graphen $G_t.$

Parameterwert berechnen

1. Schritt: $y$ -Koordinate des Tiefpunkts berechnen

$\begin{array}[t]{rll} f_t\left(\sqrt{t}\right) &=& \sqrt{t}^4 -2\cdot t\cdot \sqrt{t}^2 +8\cdot t \\[5pt] &=& t^2 -2\cdot t^2 +8\cdot t \\[5pt] &=& -t^2 +8t \\[5pt] \end{array}$

Die Funktion $y$ mit $y(t) = -t^2 +8t$ beschreibt also die $y$ -Koordinate des Tiefpunkts des Graphen von $f_t$ in Abhängigkeit von $t.$
Gesucht ist der Wert von $t,$ für den $y(t)$ maximal ist.

2. Schritt: Ableitungsfunktionen bilden

$\(\begin{array}[t]{rll} y(t) &=& -t^2 +8t \\[5pt] y$

3. Schritt: Notwendiges Kriterium anwenden

$\(\begin{array}[t]{rll} y$

4. Schritt: Hinreichendes Kriterium für Extremstellen überprüfen

$\(\begin{array}[t]{rll} y$

An der Stelle $t=4$ nimmt $y$ also ihr Maximum an. Für $t=4$ liegt der Tiefpunkt des Graphen $G_t$ also möglichst hoch.

Anzahl gemeinsamer Punkte zeigen

Betrachte für $t_1 \neq t_2:$

Vollständigen Rechenweg anzeigen

$x_1=-2$ , $x_2=2$

Für zwei beliebige verschiedene Werte $t_1$ und $t_2$ hat die Gleichung $f_{t_1}(x) = f_{t_2}(x)$ genau zwei Lösungen. Alle Graphen $f_t$ besitzen also an diesen beiden Stellen einen gemeinsamen Funtionswert. Es gibt also genau zwei Punkte, durch die alle Graphen von $f_t$ verlaufen.