Wahlteil B1
Für 
mit 
werden die Pyramiden 
mit 
und 
betrachtet (vgl. Abbildung 1).
a)
Begründe, dass das Dreieck 
gleichschenklig ist.
ist 
ist die Länge einer Höhe des Dreiecks
Bestimme den Flächeninhalt des Dreiecks.
(1 VP)
Der Mittelpunkt der Strecke Bestimme den Flächeninhalt des Dreiecks
(1 VP)
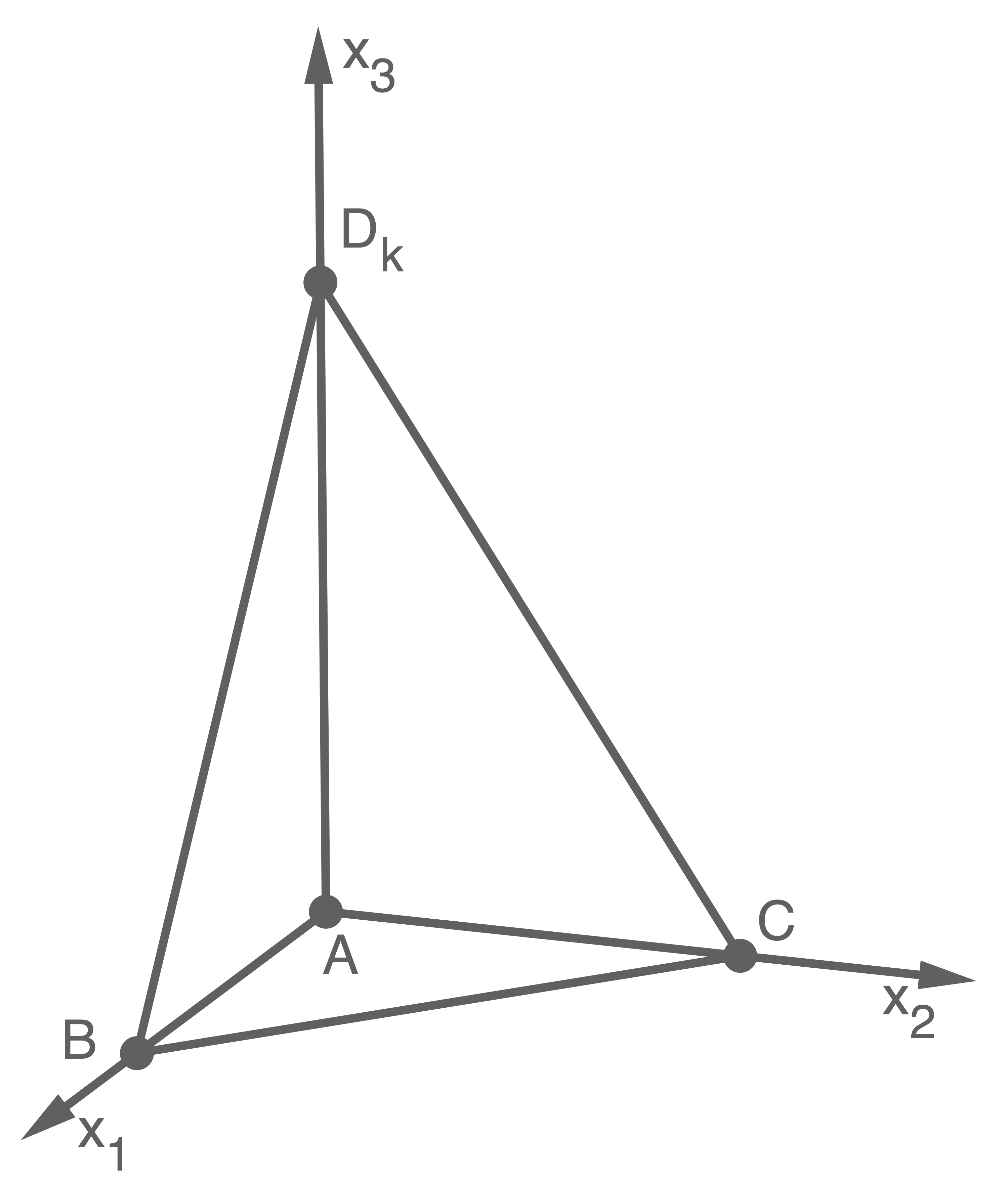
Abb. 1
b)
Ermittle denjenigen Wert von 
, für den die Größe des Winkels, unter dem die 
-Achse die Ebene 
schneidet, 
beträgt.
(2,5 VP)
c)
Zusätzlich zu den Pyramiden wird der in der Abbildung 2 gezeigte Quader betrachtet. Die Punkte 
und 
sind Eckpunkte des Quaders, die Seitenflächen des Quaders sind parallel zu den Koordinatenebenen.
Für
enthält die Seitenfläche der Pyramide den Eckpunkt 
des Quaders. Für kleinere Werte von schneidet die Seitenfläche den Quader in einem Vieleck.
Für einen Wert von verläuft die Seitenfläche durch die Eckpunkte 
und 
des Quaders. Bestimme diesen Wert von 
Teilergebnis: 
Für
Für einen Wert von
(1,5 VP)
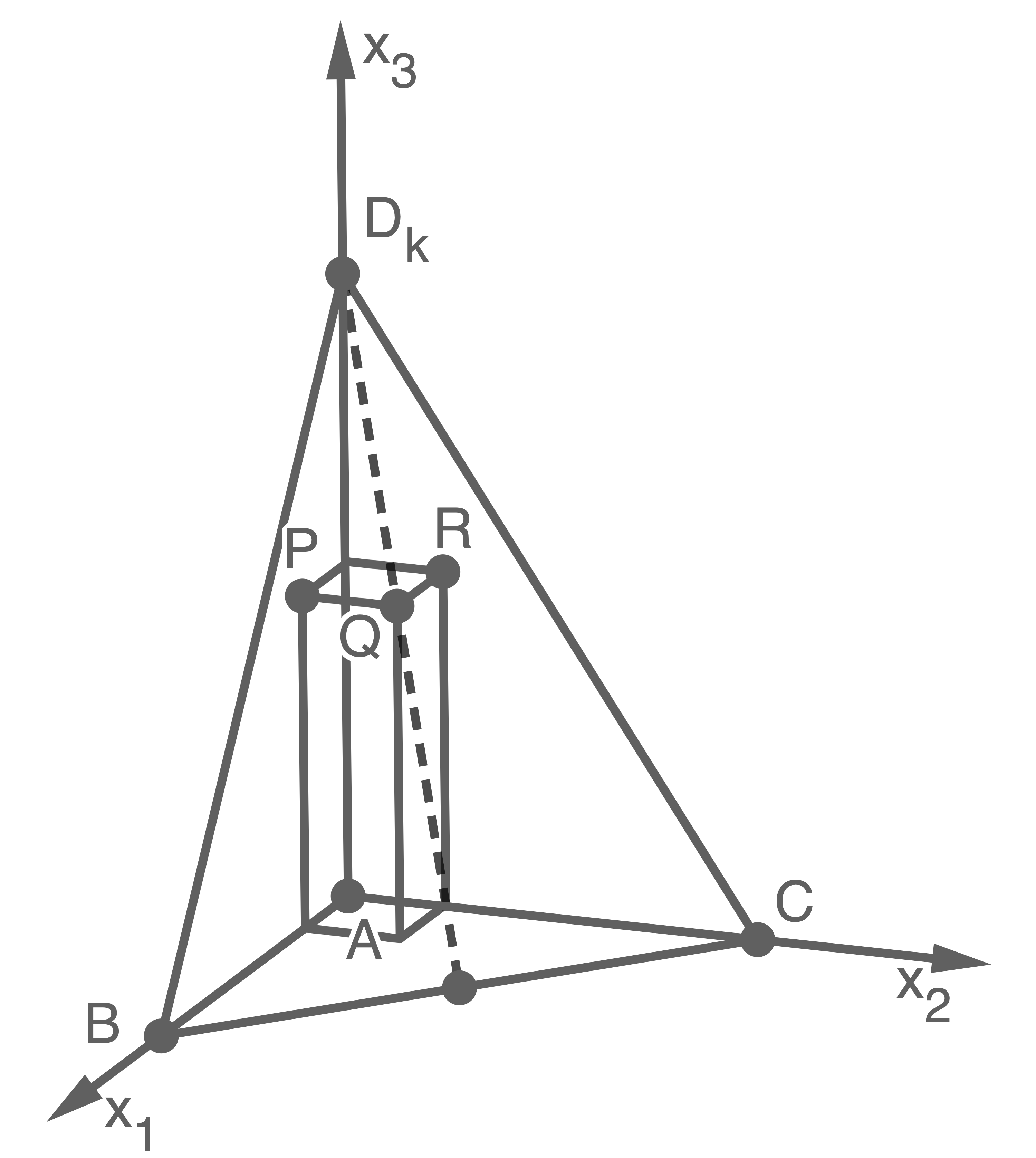
Abb. 2
(2 VP)
d)
Nun wird die Pyramide 
, d.h. diejenige für , betrachtet. Dieser Pyramide werden Quader einbeschrieben (vgl. Abbildung 3). Die Grundflächen der Quader liegen in der 
-Ebene, haben den Eckpunkt gemeinsam und sind quadratisch. Die Höhe 
der Quader durchläuft alle reellen Werte mit 
Für jeden Wert von liegt der Eckpunkt 
in der Seitenfläche 
der Pyramide.
Ermittle die Koordinaten des Punktes.
Ermittle die Koordinaten des Punktes
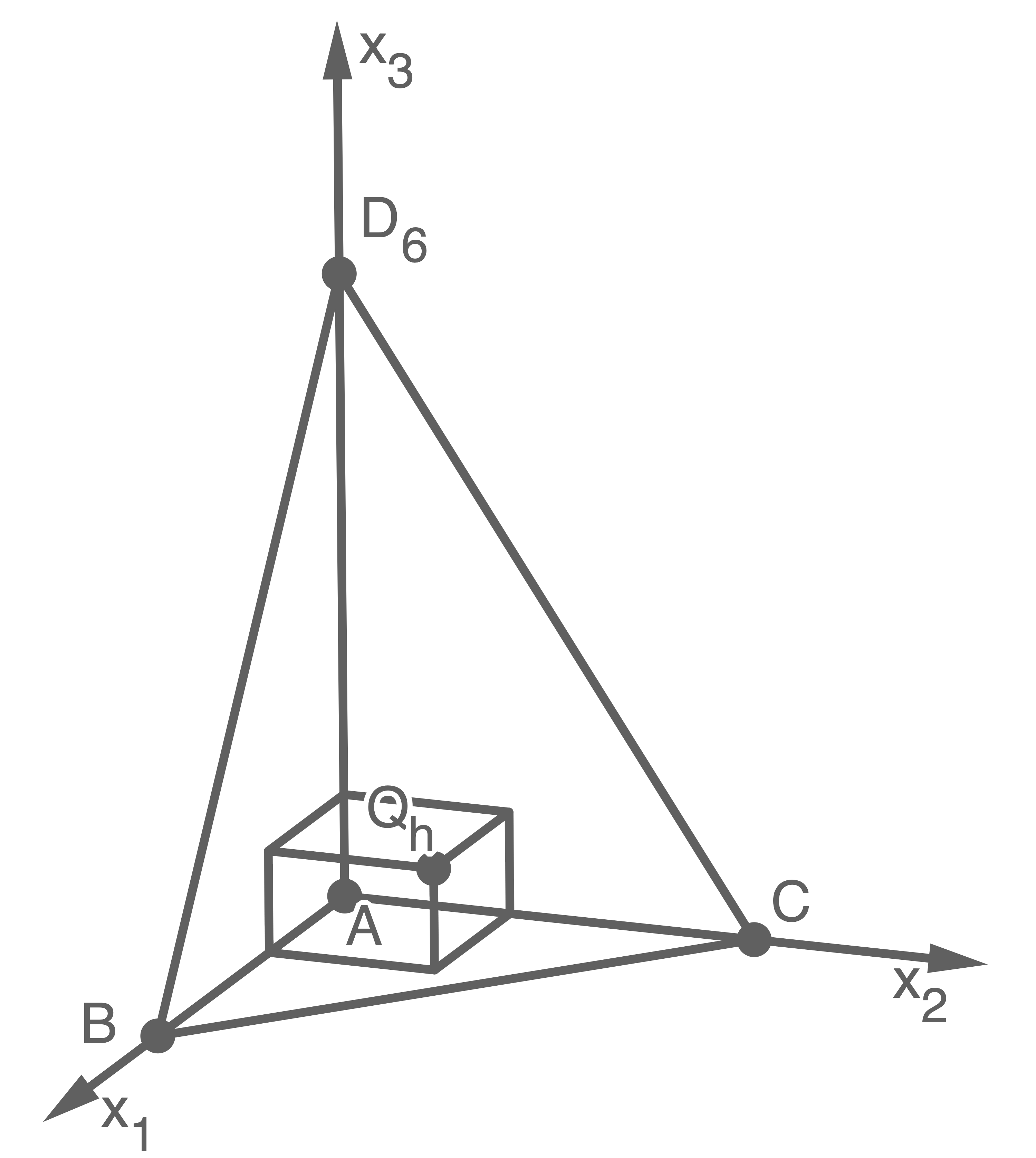
Abb. 3
(2 VP)
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
a)
Begründen der Gleichschenkligkeit
Berechnen der Streckenlängen:
Da die beiden Seiten 
und 
des Dreiecks gleich lang sind, ist das Dreieck gleichschenklig.
Flächeninhalt des Dreiecks
b)
Aus der Ebenengleichung kann ein Normalenvektor abgelesen werden: 
Allgemeine Formel:
![\(\begin{array}[t]{rll}
\sin (\alpha)&=&\dfrac{\mid g \circ n\mid}{\mid g\mid \cdot \mid n\mid } & \\[5pt]
\end{array}\)](https://mathjax.schullv.de/a1357a36a1fbdfd434c4b6cc796bd3b8d6ca29ca3df4040aae475d89690a4b85?color=5a5a5a)
Einsetzen von 
, 
und 
ergibt sich für :
Wegen 
folgt also 
c)
1. Schritt: Bestimmen der Koordinaten von und
Mit Hilfe der Abbildung sowie den Koordinaten von und ergeben sich 
und 
2. Schritt: Koordinaten von in einsetzen
![\(\begin{array}[t]{rll}
k\cdot 1 + k\cdot 0 + 4\cdot 3&=& 4k& \\[5pt]
k+ 12&=& 4k&\quad \scriptsize \mid\; -k\\[5pt]
12&=& 3k&\quad \scriptsize \mid\; :3\\[5pt]
4&=&k
\end{array}\)](https://mathjax.schullv.de/9256b235e86f1b47db2ce87a14a634d8407cd505c86554822554b2bf3796f689?color=5a5a5a)
Für verläuft also die Ebene durch den Eckpunkt und somit auch durch 
Bestimmen der Anzahl der geschnittenen Eckpunkte in Abhängigkeit von
vier Eckpunkte
fünf Eckpunkte
drei Eckpunkte
d)
Da die Grundfläche des Quaders quadratisch ist, folgt 
Bestimmen von 
durch Einsetzen der Koordinaten von in 
![\(\begin{array}[t]{rll}
6\cdot u + 6\cdot u + 4\cdot h&=& 4\cdot 6& \\[5pt]
12u + 4h &=& 24&\quad \scriptsize \mid\; -4h\\[5pt]
12u&=& 24 - 4h &\quad \scriptsize \mid\; :12\\[5pt]
u&=& 2 -\dfrac{h}{3}
\end{array}\)](https://mathjax.schullv.de/b58307ec912b6ef9fc4cf1c0703ba0afdaa8857dbb47b08e05be9d37371e1b7f?color=5a5a5a)
Die Koordinaten des Eckpunkts sind also 