Stochastik

Aufgabe III 1

Unter den Touristen eines Naturparks nutzen erfahrungsgemäß $14\,\%$ das Fahrrad für Ausflüge vor Ort. Im Folgenden werden diese Touristen als Radausflügler bezeichnet. Es soll davon ausgegangen werden, dass in einer zufälligen Auswahl von Touristen des Naturparks die Anzahl der Radausflügler binomialverteilt ist.

Für eine Stichprobe werden $300$ Touristen des Naturparks zufällig ausgewählt.

Bestimme die Wahrscheinlichkeit dafür, dass sich in der Stichprobe genau $36$ Radausflügler befinden.

(1 BE)

Ermittle die Wahrscheinlichkeit dafür, dass die Anzahl der Radausflügler in der Stichprobe um mindestens $10\,\%$ größer ist als der Erwartungswert für diese Anzahl.

(3 BE)

Um den Naturpark als Reiseziel attraktiver zu machen, setzt der dortige Tourismusverband Shuttlebusse ein. Die Fahrkarten für diese Busse können ausschließlich online gebucht werden und sind jeweils für einen bestimmten Tag gültig. Erfahrungsgemäß werden $80\,\%$ aller gebuchten Fahrkarten spätestens am Vortag der Fahrt gebucht. Von diesen spätestens am Vortag gebuchten Fahrkarten werden $90\,\%$ auch tatsächlich genutzt. Bei den restlichen, erst am Tag der Fahrt gebuchten Fahrkarten liegt dieser Anteil mit $95\,\%$ etwas höher.

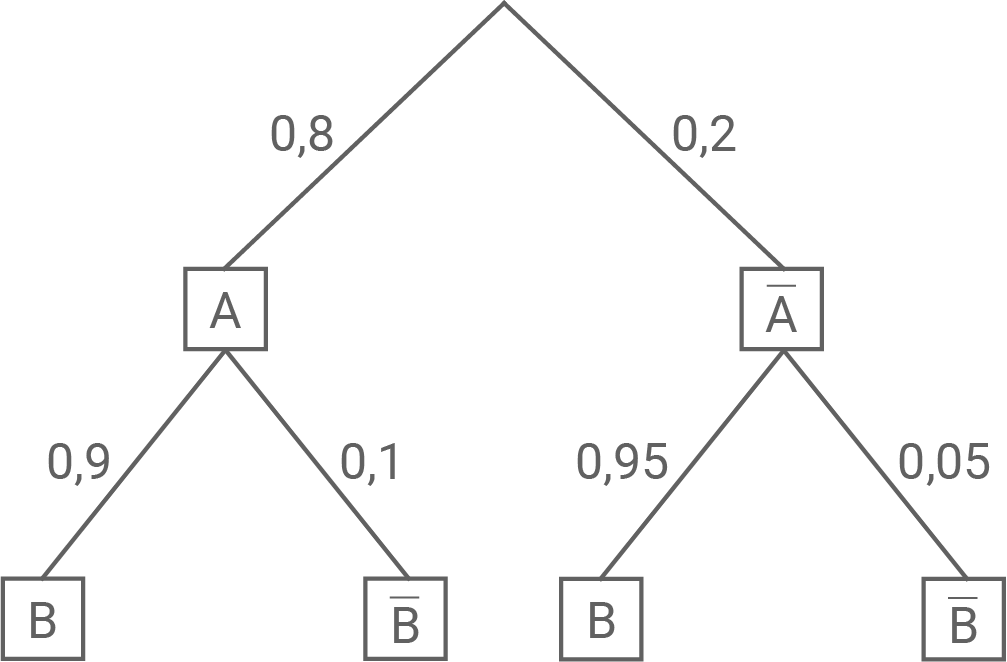
Stelle den Sachverhalt in einem beschrifteten Baumdiagramm dar.

(3 BE)

Betrachtet wird eine zufällig ausgewählte, nicht genutzte Fahrkarte. Beurteile die folgende Aussage:

Die Wahrscheinlichkeit dafür, dass diese Fahrkarte spätestens am Vortag gebucht wurde, ist achtmal so groß wie die Wahrscheinlichkeit dafür, dass sie erst am Tag der Fahrt gebucht wurde.

(3 BE)

Der Tourismusverband vermutet, dass sich der bisherige Anteil der Radausflügler unter den Touristen von $14\,\%$ durch den Einsatz der Shuttlebusse erhöht hat. Die Verantwortlichen planen die Durchführung eines Signifikanztests mit einem Signifikanzniveau von $8\,\%$ und der Nullhypothese „Der Anteil der Radausflügler unter allen Touristen liegt bei höchstens $14\,\%$ .“ Vor der Durchführung des Tests wird festgelegt, die Shuttlebusse nur dann weiterzubetreiben, wenn die Nullhypothese aufgrund des Testergebnisses abgelehnt wird.

Es ist geplant, den Test auf der Grundlage einer Stichprobe von $500$ Touristen durchzuführen. Bestimme die zugehörige Entscheidungsregel.

(5 BE)

Angenommen, der beschriebene Test wird auf der Grundlage einer Stichprobe von nur $200$ Touristen durchgeführt. In diesem Fall wird die Nullhypothese abgelehnt, wenn sich unter diesen mehr als $35$ Radausflügler befinden. Damit die Wahrscheinlichkeit für den Fehler zweiter Art höchstens $15\,\%$ beträgt, muss der tatsächliche Anteil der Radausflügler unter allen Touristen mindestens einen bestimmten Wert haben.
Ermittle diesen Wert auf ganze Prozent genau und beschreibe die Bedeutung des Fehlers zweiter Art im Sachzusammenhang.

(5 BE)

Aufgabe III 2

Die Zufallsgröße $Z$ gibt die Fahrzeit eines Linienbusses zwischen zwei bestimmten Haltestellen an. Sie kann näherungsweise als normalverteilt mit dem Erwartungswert $\mu = 200$ und der Standardabweichung $\sigma = 30$ angenommen werden (alle Werte in Sekunden).

Bestimme die Wahrscheinlichkeit dafür, dass bei einer zufällig ausgewählten Fahrt die Fahrzeit zwischen den beiden Haltestellen weniger als $150$ Sekunden beträgt.

(1 BE)

Ermittle das kleinste Intervall, in dem die Fahrzeit einer zufällig ausgewählten Fahrt mit einer Wahrscheinlichkeit von $60\,\%$ liegt.

(4 BE)

Berechne die Wahrscheinlichkeit dafür, dass von zehn zufällig ausgewählten Fahrten die Fahrzeit bei genau zwei Fahrten mehr als $220$ Sekunden beträgt.

(3 BE)

An Markttagen ist die Fahrzeit zwischen den beiden Haltestellen durchschnittlich etwas länger als an den übrigen Tagen. Diese Fahrzeit kann durch die normalverteilte Zufallsgröße $Z^*$ beschrieben werden.

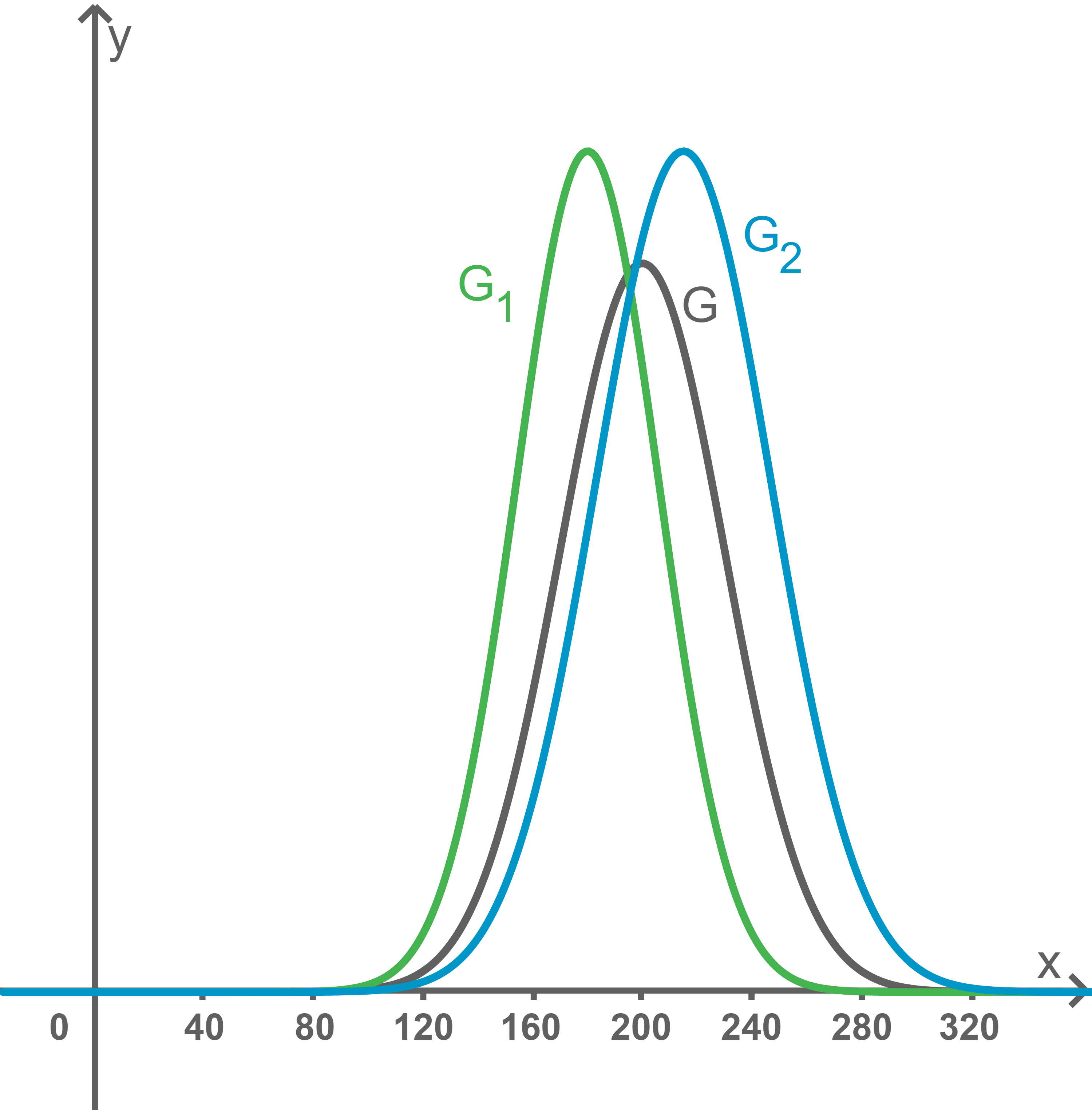
In der Abbildung ist $G$ der Graph der Dichtefunktion von $Z.$ Untersuche, ob einer der Graphen $G_1$ und $G_2$ der Graph der Dichtefunktion von $Z^*$ sein könnte.

(2 BE)

Eine Fahrt mit einer Fahrzeit von mehr als $240$ Sekunden zwischen den beiden Haltestellen gilt als verspätet. Dies ist bei $9\,\%$ aller Fahrten der Fall. $20\,\%$ aller Fahrten finden an Markttagen statt. Ein Viertel der Fahrten an Markttagen ist verspätet.
Zu einer zufällig ausgewählten Fahrt werden folgende Ereignisse betrachtet:

$V:$

„Die Fahrt ist verspätet.“

$M:$

„Die Fahrt findet an einem Markttag statt.“

Stelle den Sachverhalt in einer vollständig ausgefüllten Vierfeldertafel dar.

(4 BE)

Von den Fahrten ohne Verspätung wird eine Fahrt zufällig ausgewählt. Bestimme die Wahrscheinlichkeit dafür, dass diese an einem Tag ohne Markt stattfindet.

(2 BE)

Eine städtische Mitarbeiterin hält $240$ Sekunden als Grenze, ab der eine Fahrt als verspätet gilt, für zu streng. Deshalb schlägt sie vor, eine neue Grenze so festzulegen, dass nur noch $15\,\%$ der Fahrten an einem Markttag als verspätet gelten. Mit dieser neuen Grenze treten bei diesen verspäteten Fahrten an einem Markttag dann in $51\,\%$ der verspäteten Fahrten ein Markttag als Ursache auf.

Berechne die neue Grenze.

(4 BE)

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?

Lösung III 1

Die Zufallsvariable $X,$ die die Anzahl der Radausflügler angibt, ist binomialverteilt mit $n=300$ und $p=0,14.$ Für die gesuchte Wahrscheinlichkeit folgt somit:

Rechenweg anzeigen

$P_{0,14}^{300}(X=36) \approx 4,2\,\%$

Für den Erwartungswert gilt:

$\mu=n\cdot p=300\cdot0,14=42$

Es gilt $42\cdot0,1=4,2$ und $42+4,2=46,2.$ Damit folgt für die gesuchte Wahrscheinlichkeit:

$\begin{array}[t]{rlll} P_{0,14}^{300}(X\geq46,2)&=&P_{0,14}^{300}(X\geq47) \\[5pt] &=&1-P_{0,14}^{300}(X\leq46) \\[5pt] &\approx&1-0,7757 \\[5pt] &=&0,2243 \\[5pt] &=&22,43\,\% \end{array}$

$A:$

„Die Fahrkarte wird spätestens am Vortag gebucht.“

$B:$

„Die Fahrkarte wird tatsächlich genutzt.“

$\begin{array}[t]{rlll} P_\overline{B}(A)&=& \dfrac{P\left(\overline{B}\cap A\right)}{P\left(\overline{B}\right)} \\[5pt] &=&\dfrac{0,8\cdot0,1}{P\left(\overline{B}\right)} \\[5pt] &=&\dfrac{0,08}{P\left(\overline{B}\right)} \end{array}$

$\begin{array}[t]{rlll} P_\overline{B}\left(\overline{A}\right)&=& \dfrac{P\left(\overline{B}\cap \overline{A}\right)}{P\left(\overline{B}\right)} \\[5pt] &=&\dfrac{0,2\cdot0,05}{P\left(\overline{B}\right)} \\[5pt] &=&\dfrac{0,01}{P\left(\overline{B}\right)} \end{array}$

Damit folgt:

$\begin{array}[t]{rlll} 8\cdot P_\overline{B}\left(\overline{A}\right)&=&8\cdot\dfrac{0,01}{P\left(\overline{B}\right)} \\[5pt] &=&\dfrac{0,08}{P\left(\overline{B}\right)} \\[5pt] &=&P_\overline{B}(A) \end{array}$

Die Aussage aus der Aufgabenstellung ist somit richtig.

Die Nullhypothese liefert $p_0\leq0,14.$ Die Zufallsvariable $Y,$ die die Anzahl der Radausflügler angibt, ist somit binomialverteilt mit $n=500$ und $p=0,14$ und es wird der kleinstmögliche Wert von $k$ gesucht, sodass gilt:

$P_{0,14}^{500}(P\geq k)\leq8\,\%$

Stichprobenartiges Ausprobieren mit dem Taschenrechner liefert:

$\begin{array}[t]{rlll} P_{0,14}^{500}(P\geq 81)&=&1-P_{0,14}^{500}(P\leq 80) \\[5pt] &\approx&1-0,9102 \\[5pt] &=&0,0898 \\[5pt] &=&8,98\,\% \end{array}$

$\begin{array}[t]{rlll} P_{0,14}^{500}(P\geq 82)&=&1-P_{0,14}^{500}(P\leq 81) \\[5pt] &\approx&1-0,9286 \\[5pt] &=&0,0714 \\[5pt] &=&7,14\,\% \end{array}$

Die zugehörige Entscheidungsregel lautet somit, dass die Nullhypothese dann abgelehnt wird, wenn sich mindestens $82$ Radausflügler in der Stichprobe befinden.

Wert ermitteln

Es wird die kleinstmögliche Wahrscheinlichkeit $p$ gesucht, sodass gilt:

$P_p^{200}(X\leq35)\leq15\,\%$

Systematisches Ausprobieren mit dem Taschenrechner liefert:

$\begin{array}[t]{rlll} P_{0,2}^{200}(P\leq 35)&\approx&0,2151 \\[5pt] &=&21,51\,\% \\[5pt] &\approx&22\,\% \end{array}$

$\begin{array}[t]{rlll} P_{0,21}^{200}(P\leq 35)&\approx&0,1284 \\[5pt] &=&12,84\,\% \\[5pt] &\approx&13\,\% \end{array}$

Der tatsächliche Anteil der Radausflügler muss somit mindestens $21\,\%$ betragen.

Sachzusammenhang beschreiben

Die Verantwortlichen entscheiden sich dafür, den Betrieb der Shuttlebusse einzustellen, obwohl der Anteil der Radausflügler auf über $14\,\%$ gestiegen ist.

Lösung III 2

Mit dem Taschenrechner folgt für die gesuchte Wahrscheinlichkeit:

$P(Z\lt150)\approx0,05=5\,\%$

Das kleinste solche Intervall muss symmetrisch um den Erwartungswert $\mu$ liegen. Die Warscheinlichkeit außerhalb des gesuchten Intervalls zu liegen beträgt $40\,\%.$ Somit folgt aus $P(Z\leq a)=0,2$ mit dem Taschenrechner durch systematisches Ausprobieren:

$a\approx174,8$

Da $200-174,8=25,2$ gilt, folgt für das gesuchte Intervall:

$[174,8;225,2]$

Für die Wahrscheinlichkeit, dass eine Fahrtzeit mehr als 220 Sekunden dauert, gilt:

$P(Z\gt220)\approx0,25$

Die Zufallsvariable $X$ gibt die Anzahl der Fahrten an, die länger als 220 Sekunden dauern, und ist binomialverteilt mit Parametern $n=10$ und $p=0,25.$ Für die gesuchte Wahrscheinlichkeit folgt damit:

$\begin{array}[t]{rlll} P_p^{10}(X=2)&=&P_p^{10}(X\leq2)-P_p^{10}(X\leq1) \\[5pt] &\approx&0,5256-0,244 \\[5pt] &=&0,2816 \\[5pt] &=&28,16\,\% \end{array}$

Der Graph $G_1$ ist gegenüber $G$ nach links verschoben. Somit kann dieser Graph nicht zu $Z^*$ gehören, da die durch diese Zufallsvariable beschriebene Fahrtzeit durchschnittlich länger ist.
Der Graph $G_2$ kann ebenfalls nicht zu $Z^*$ gehören, da der Inhalt der Fläche zwischen $G_2$ und der $x$ -Achse größer ist als der Inhalt der Fläche zwischen $G$ und der $x$ -Achse.

	$\color{#fff}{V}$	$\color{#fff}{\overline{V}}$
$\color{#fff}{M}$	$0,05$	$0,15$	$0,2$
$\color{#fff}{\overline{M}}$	$0,04$	$0,76$	$0,8$
	$0,09$	$0,91$	$1$

$\begin{array}[t]{rlll} P_\overline{V}\left(\overline{M}\right)&=&\dfrac{P\left(\overline{V}\cap\overline{M}\right)}{P\left(\overline{V}\right)} \\[5pt] &=&\dfrac{0,76}{0,91} \\[5pt] &\approx&0,835 \\[5pt] &=&83,5\,\% \end{array}$

Mit den neuen Werten folgt:

$P(V \cap M)=0,15 \cdot 0,2=0,03$

Für die Wahrscheinlichkeit einer verspäteten Fahrt folgt damit:

$\begin{array}[t]{rlll} P(V)&=&\dfrac{P(V \cap M)}{P_V(M)} \\[5pt] &=&\dfrac{0,03}{0,51} \\[5pt] &=&\dfrac{1}{17} \end{array}$

Die neue Grenze $t$ kann nun mit der Ungleichung $P(Z\geq t)=\frac{1}{17}$ bestimmt werden. Systematisches Ausprobieren mit dem Taschenrechner liefert:

$t\approx247$

Die neue Grenze würde damit bei ca. $247$ Sekunden liegen.

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?