Wahlaufgaben

Für jedes $a\gt0$ ist eine in $\mathbb{R}$ definierte Funktion $f_a$ gegeben durch $f_a(x)=x \cdot \mathrm e^{\frac{x}{a}}.$
Der Graph jeder Funktion $f_a$ besitzt einen Extrempunkt $E_a.$ Weise nach, dass es eine Ursprungsgerade gibt, auf der alle Punkte $E_a$ liegen.

(5 BE)

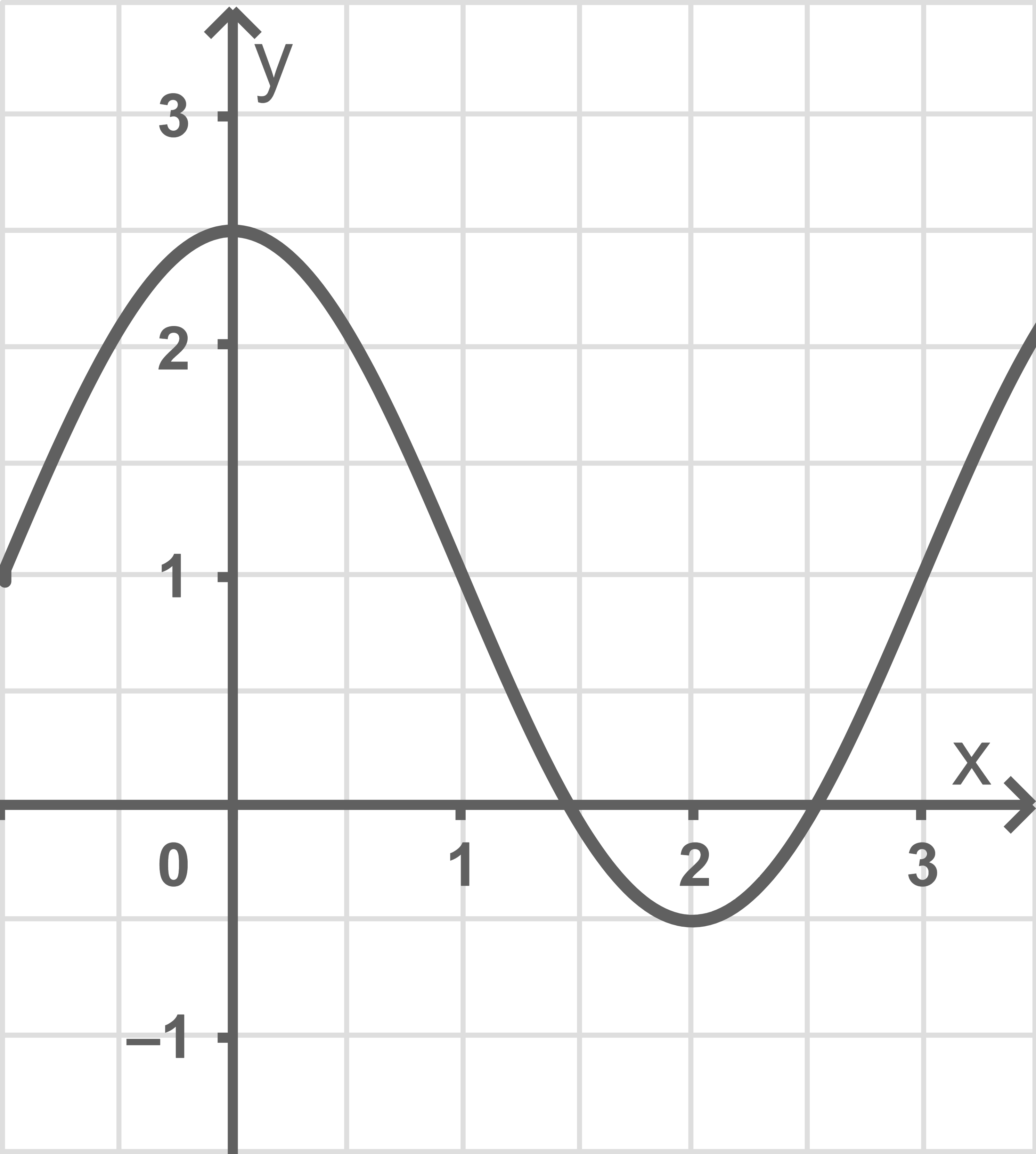
Abgebildet ist der Graph der in $\mathbb{R}$ definierten Funktion $f$ mit $f(x)=a \cdot \cos \left(\frac{\pi}{2} \cdot x\right)+b;$ dabei sind $a$ und $b$ reelle Zahlen.

Gib die Werte von $a$ und $b$ an.

(2 BE)

Gegeben ist die Funktion $J_0$ durch $J_0(x)=\displaystyle\int_{0}^{x}f(t)\;\mathrm dt$ mit $x \in ]0 ; \infty[.$ Begründe ohne Rechnung, dass der Graph von $J_0$ keinen Schnittpunkt mit der $x$ -Achse hat.

(3 BE)

Die Punkte $A(8\mid0\mid 0), B(0\mid6\mid 0)$ und $C(4\mid3\mid 10)$ sind die Eckpunkte eines gleichschenkligen Dreiecks mit Basis $\overline{AB}.$ Das Dreieck $ABC$ wird so um die Achse $AB$ gedreht, dass der entstehende Punkt $C^*$ in der $x_1 x_2$ -Ebene liegt. Bestimme die Koordinaten eines möglichen Punkts $C^*.$

(5 BE)

Der abgebildete Körper $ABCDEFGH$ ist Teil einer geraden Pyramide mit rechteckiger Grundfläche $EFGH.$ Die Rechtecke $ABCD$ und $EFGH$ liegen in zwei zueinander parallelen Ebenen mit dem Abstand $5.$ Der Flächeninhalt von EFGH ist viermal so groß wie der von $ABCD.$ Es gilt:

$A(0\mid0\mid 0), B(4\mid0\mid 0),$ $C(4\mid6\mid 0)$ und $D(0\mid6\mid 0)$

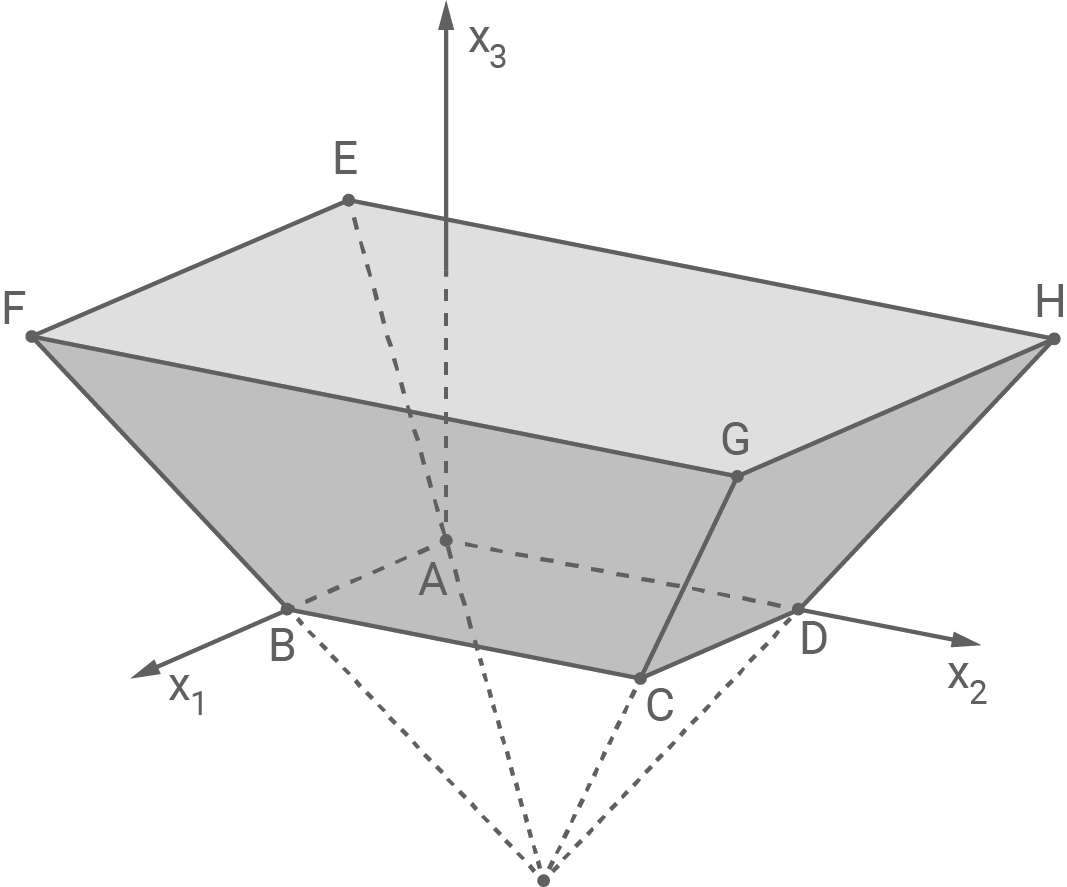
Gib eine Gleichung einer der beiden Symmetrieebenen des Körpers $ABCDEFGH$ an.

(1 BE)

Begründe, dass die Koordinaten des Punkts $F$ mit folgendem Term ermittelt werden können:

$\pmatrix{2\\3\\5}+2\cdot\left(\pmatrix{4\\0\\0}-\pmatrix{2\\3\\0}\right)$

(4 BE)

Betrachtet wird ein Würfel, dessen Seiten mit den Zahlen von 1 bis 6 durchnummeriert sind.

Der Würfel wird zweimal geworfen. Die Zufallsgröße $X$ gibt das Produkt der dabei erzielten Zahlen an. Begründe, dass $P(X=10)=P(X=15)$ ist.

(2 BE)

Nun wird der Würfel $n$ -mal geworfen, wobei $n$ größer als $2$ ist. Ermittle einen Term, mit dem man die Wahrscheinlichkeit für das folgende Ereignis berechnen kann: „Das Produkt der $n$ erzielten Zahlen ist $2, 3$ oder $5.$ “

(3 BE)

Zu einem Zufallsexperiment werden zwei stochastisch unabhängige Ereignisse $A$ und $B$ betrachtet. Es gilt $P(B)=P(A)+0,6$ sowie $P\left(A \cap \overline{B}\right)=0,04.$ Bestimme $P(A).$

(5 BE)

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?

Für die Ableitung von $f$ folgt:

$\(\begin{array}[t]{rlll} f_a$

Anwenden der notwendigen Bedingung für Extremstellen liefert:

$\(\begin{array}[t]{rlll} f_a$

Da die $\mathrm e$ -Funktion stets ungleich Null ist, folgt mit dem Satz des Nullprodukts:

$\begin{array}[t]{rlll} 1+\dfrac{x}{a}&=&0 &\mid\;-1 \\[5pt] \dfrac{x}{a}&=&-1 &\mid\;\cdot a \\[5pt] x&=&-a \end{array}$

Da laut Aufgabenstellung der Graph jeder Funktion $f_a$ einen Extrempunkt besitzt, kann auf die Überprüfung der hinreichenden Bedindung verzichtet werden und es folgt, dass $f_a$ bei $x=-a$ eine Extremstelle besitzt. Für den Funktionswert folgt:

$\begin{array}[t]{rlll} f_a(-a)&=&-a\cdot\mathrm e^{-\frac{a}{a}} \\[5pt] &=&-\dfrac{a}{\mathrm e} \end{array}$

Für die Steigung der Geraden, die durch den Koordinatenursprung und den Extrempunkt von $f_a$ verläuft folgt somit:

$\dfrac{f_a(-a)-0}{-a-0}=\dfrac{-\frac{a}{\mathrm e}}{-a}=\dfrac{1}{\mathrm e}$

Da diese Steigung nicht von $a$ abhängt folgt somit, dass alle Extrempunkte der Schar $f_a$ auf der gleichen Ursprungsgeraden liegen.

Die Variable $a$ streckt bzw. staucht in $y$ -Richtung, während $b$ in bzw. gegen $y$ -Richtung verschiebt. Der abgebildete Graph besitzt eine Amplitude von $1,5$ und seine Hochpunkte liegen auf der Geraden $y=2,5.$
Da der Kosinus eine Amplitude von $1$ besitzt und seine Hochpunkte auf der Geraden $y=1$ liegen folgt somit, dass $a=1,5$ und $b=1$ gilt.

Die Funktion $J_0$ gibt für einen Wert $x$ den orientierten Flächeninhalt zwischen dem Graphen von $f$ und der $x$ -Achse im Bereich von $0$ bis $x$ an. Da $f$ sich nur durch Verschiebung und Streckung von der Kosinusfunktion unterscheidet, ist die Funktion ebenfalls periodisch. Die Abbildung zeigt zudem, dass die Inhalte der Teilflächen, die der Graph von $f$ mit der $x$ -Achse oberhalb dieser einschließt, größer sind als die Inhalte der Teilflächen unterhalb der $x$ -Achse.
Da der Graph von $f$ bis zur ersten Nullstelle außerdem oberhalb der $x$ -Achse verläuft und dort eine größere Fläche einschließt, als die darauffolgende Fläche unterhalb der $x$ -Achse, besitzt der Graph von $J_0$ im Intervall $] 0 ; \infty[$ somit keinen Schnittpunkt mit der $x$ -Achse.

Aus den Koordinaten von $A$ und $B$ folgt direkt, dass $M(4\mid3\mid0)$ für die Koordinaten des Mittelpunkts $M$ der Strecke $\overline{AB}$ gilt. Da sowohl $A$ als auch $B$ in der $x_1x_2$ -Ebene liegen, ist die Höhe $\left\vert\overrightarrow{MC}\right\vert$ des Dreiecks $ABC$ zudem durch die $x_3$ -Koordinate von $C$ gegeben und beträgt somit $10\;\text{LE}.$

Der gesuchte Punkt $C^*$ liegt ebenfalls in der $x_1x_2$ -Ebene, sodass die Höhe des neuen Dreiecks auch entlang eines Vektors, der parallel zur $x_1x_2$ -Ebene liegt, verläuft. Dieser Vektor besitzt somit die $x_3$ -Koordinate $0.$

Da dieser Vektor zudem orthogonal zu $\overrightarrow{AB}=\pmatrix{-4\\3\\0}$ sein muss, ergibt sich als ein möglicher Vektor direkt:

$\overrightarrow{v}=\pmatrix{3\\4\\0}$

Für die Länge dieses Vektors folgt:

$\begin{array}[t]{rlll} \left\vert\overrightarrow{v}\right\vert&=&\left\vert\pmatrix{3\\4\\0}\right\vert \\[5pt] &=&\sqrt{3^2+4^2+0^2} \\[5pt] &=&\sqrt{25} \\[5pt] &=&5\;[\text{LE}] \end{array}$

Da die Höhe des Dreiecks, gegeben durch $10\;\text{LE},$ sich durch die Drehung nicht verändert, folgt als ein möglicher Punkt $C^*:$

$\begin{array}[t]{rlll} \overrightarrow{OC^*}&=&\overrightarrow{OM}+2\cdot\overrightarrow{v} \\[5pt] &=&\pmatrix{4\\3\\0}+2\cdot\pmatrix{3\\4\\0} \\[5pt] &=&\pmatrix{10\\11\\0} \end{array}$

Die Koordinaten eines möglichen Punkts $C^*$ sind somit durch $C^*(10\mid11\mid0)$ gegeben.

Eine mögliche Ebenengleichung ist gegeben durch $x_1=2.$

Da die Pyramide gerade ist, unterscheiden sich die Koordinaten der Mittelpunkte der beiden Rechtecke $ABCD$ und $EFGH$ nur in der $x_3$ -Koordinate. Anhand der Koordinaten der Eckpunkte des Rechtecks $ABCD$ folgt für den Mittelpunkt direkt:

$M(2\mid3\mid0)$

Mit der Anmerkung aus der Aufgabenstellung, dass die beiden Rechtecke um $5\;\text{LE}$ auseinander liegen, und der Darstellung der Pyramide in der Abbildung folgt für die Koordinaten des Mittelpunkts des Rechtecks $EFGH$ direkt $\(M$

Die Aufgabenstellung liefert zudem, dass der Flächeninhalt von $EFGH$ viermal so groß ist, wie der von $ABCD.$ Da die Pyramide gerade ist, sind die beiden Rechtecke ähnlich und es gilt somit, dass die Diagonalen von $EFGH$ doppelt so lang sind wie die von $ABCD.$ Insgesamt folgt damit für den Ortsvektor des Punktes $F:$

$\(\begin{array}[t]{rlll} \overrightarrow{OF}&=&\overrightarrow{OM$

Sowohl $10$ als auch $15$ können jeweils nur durch genau ein Produkt von zwei Zahlen erhalten werden, nämlich das Produkt von $2$ und $5$ bzw. das Produkt von $3$ und $5.$ Hierbei ist egal, in welcher Reihenfolge die beiden Zahlen gewürfelt werden, d.h. es gibt jeweils zwei Ergebnisse, die $X=10$ bzw. $X=15$ liefern. Da jede zahl auf dem Würfel mit gleicher Wahrscheinlichkeit erzielt wird, gilt damit $P(X=10)=P(X=15).$

Die Zahlen $2,3$ und $5$ sind Primzahlen. Somit ist die einzige Möglichkeit, dass das Produkt der $n$ erzielten Zahlen $2,3$ oder $5$ ist, dass $(n-1)$ -mal die Zahl $1$ gewürfelt wird, und einmal $2,3$ bzw. $5.$ Da es $n$ mögliche Würfe gibt, in denen die Zahl ungleich $1$ gewürfelt werden kann, folgt für die gesuchte Wahrscheinlichkeit $p$ somit:

$p=3\cdot n\cdot\dfrac{1}{6}\cdot\left(\dfrac{1}{6}\right)^{n-1}$

Da die Ereignisse stochastisch unabhängig sind, gilt $P(A)\cdot P\left(\overline{B}\right)=P\left(A\cap\overline{B}\right).$ Wenn $P(A)=x$ gesetzt wird, ergibt sich somit:

Rechenweg anzeigen

$x^2-0,4x+0,04=0$

Mit der $pq$ -Formel folgt:

$\begin{array}[t]{rlll} x_{1;2}&=&\dfrac{0,4}{2}\pm\sqrt{\left(\dfrac{0,4}{2}\right)^2-0,04} \\[5pt] &=&0,2\pm\sqrt{0} \\[5pt] &=&0,2 \end{array}$

Somit gilt $P(A)=x=0,2.$

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?