Analytische Geometrie

Aufgabe II 1

Die Abbildung zeigt die Pyramide $ABCDS.$ Ihre Grundfläche $ABCD$ ist ein Drachenviereck mit den Eckpunkten $A(0\mid 0\mid 0),$ $B(2\mid 2\mid 0),$ $C(0\mid 6\mid 0)$ und $D(-2\mid 2\mid 0).$ Die Spitze der Pyramide liegt im Punkt $S(0\mid 0\mid 6).$

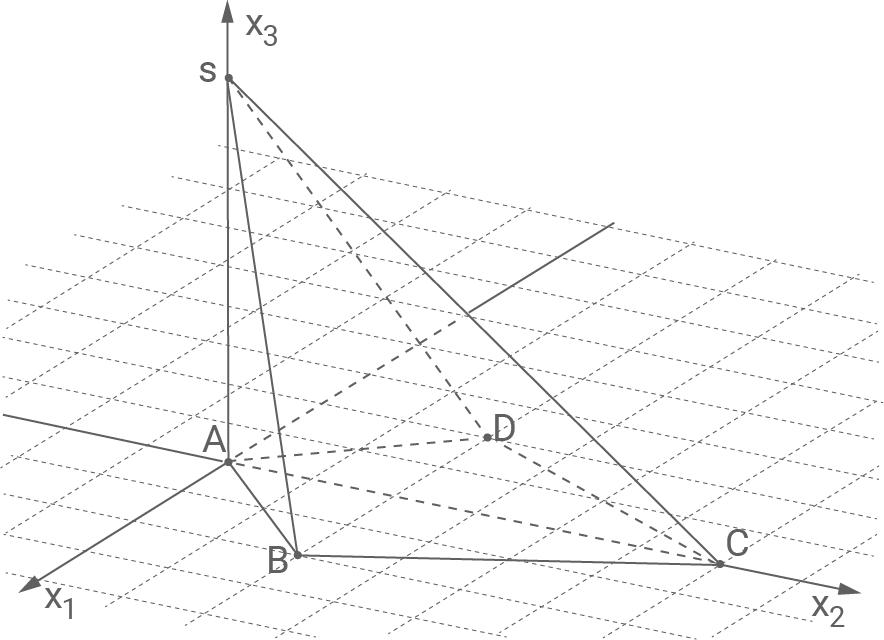
Berechne die Länge der kürzesten der acht Kanten sowie das Volumen der Pyramide $ABCDS.$

(4 BE)

Die Seitenfläche $BCS$ der Pyramide liegt in der Ebene $E.$

Betrachtet werden die Vektoren $\pmatrix{n_1\\n_2\\n_3}$ , deren Koordinaten nicht alle gleich null sind. Begründe, dass ein solcher Vektor, für den $\pmatrix{n_1\\n_2\\n_3} \circ\pmatrix{-1\\2\\0}=0$ und $\pmatrix{n_1\\n_2\\n_3} \circ\pmatrix{-1\\-1\\3}=0$ gilt, ein Normalenvektor von $E$ ist.

(3 BE)

Die Ebene $E$ hat die Gleichung $2 x_1+x_2+x_3=6.$ Bestimme die Größe des Winkels, den $E$ mit der $x_1x_2$ -Ebene einschließt.

(3 BE)

Gegeben ist die Schar der Ebenen $F_k: k \cdot x_2+(k-2) \cdot x_3=2 k$ mit $k \in\;] 0 ; 3[.$ Jede Ebene $F_k$ der Schar schneidet die Pyramide $A B C D S$ in einem Dreieck $BD Q_k,$ wobei der Punkt $Q_k$ auf der Strecke $\overline{SC}$ liegt.

Gib eine Gleichung der Ebene $F_2$ an und zeichne in die Abbildung in der Anlage die Schnittfigur von $F_2$ mit der Pyramide $ABCDS$ ein.

(4 BE)

Es gibt einen Wert von $k,$ für den der Flächeninhalt des Dreiecks $BDQ_k$ minimal ist. Ermittle diesen Wert.

(6 BE)

Aufgabe II 2

Gegeben ist die Ebene $F: x_1-3 x_2-x_3=-6.$

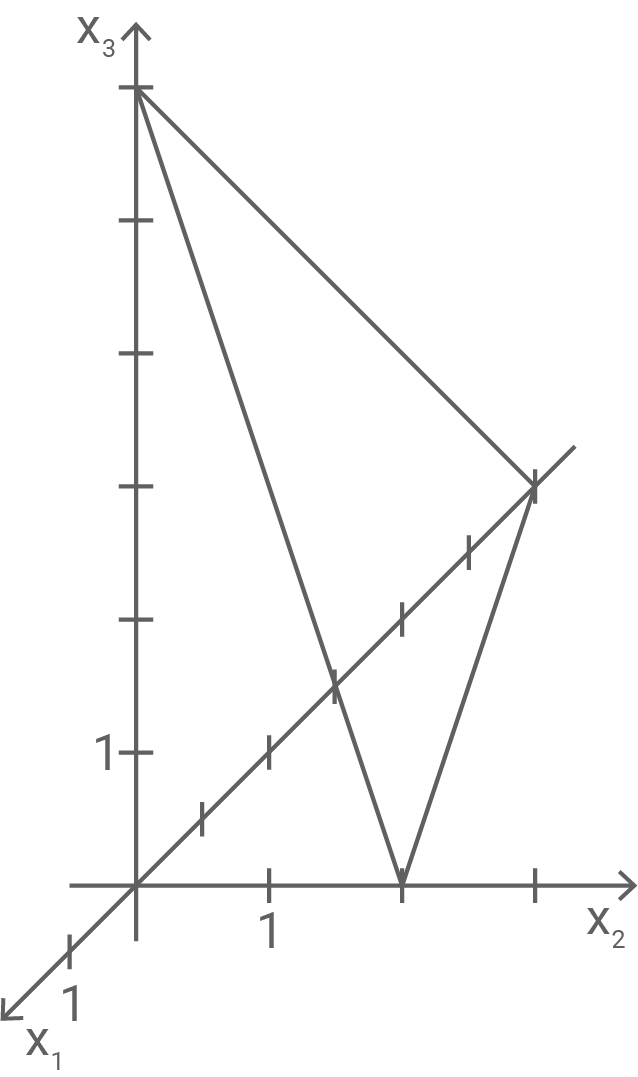
Stelle $F$ in einem Koordinatensystem dar.

(2 BE)

Berechne die Größe des Winkels, den $F$ mit der Ebene $G: -2 x_1+6 x_2=8$ einschließt.

(3 BE)

Betrachtet wird die Schar der Ebenen $E_k: 2 x_1-6 x_2+(4-k) \cdot x_3=-2 k$ mit $k \in \mathbb{R}$ .

Die Ebene $F$ gehört zu dieser Schar. Gib den zugehörigen Wert von $k$ an.

(1 BE)

Für einen Wert von $k$ ist $E_{k}$ orthogonal zu $F.$ Ermittle diesen Wert von $k.$

(3 BE)

Für jedes $k$ mit $0,4\lt k\lt3,6$ sind die Spurpunkte von $E_k$ auf der $x_1$ - und der $x_2$ -Achse und der Punkt $\left(0\,\bigg\vert\,\frac{4}{3}\,\bigg\vert\,0\right)$ die Eckpunkte eines Dreiecks $D_k.$ Einer der drei abgebildeten Graphen stellt den Flächeninhalt von $D_k$ in Abhängigkeit von $k$ dar. Entscheide, welcher Graph das ist, und begründe deine Entscheidung.

I
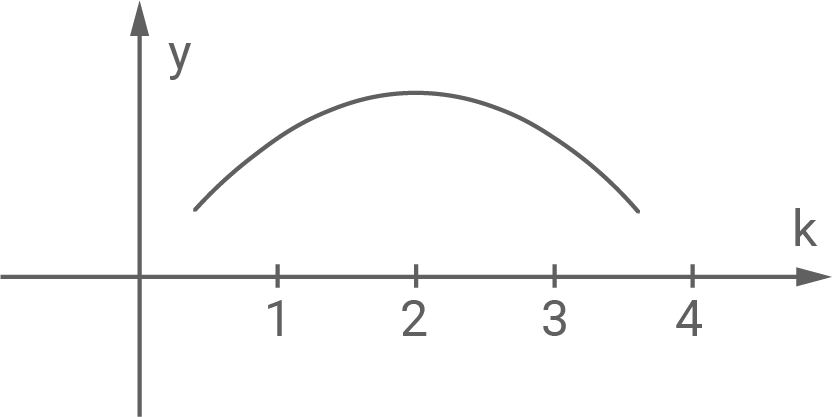
II
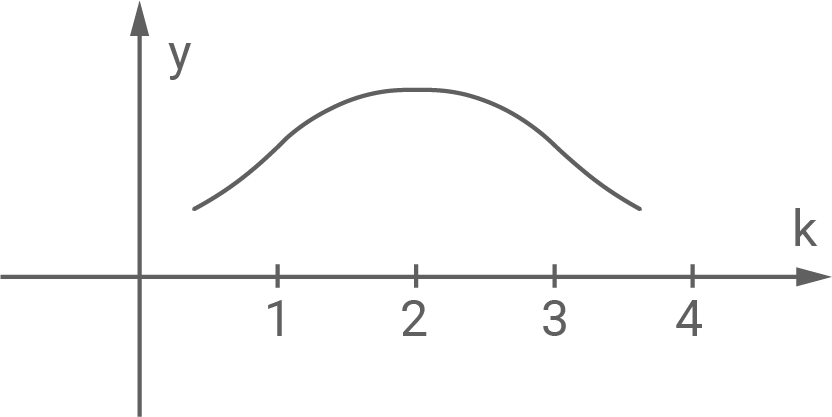
III

(4 BE)

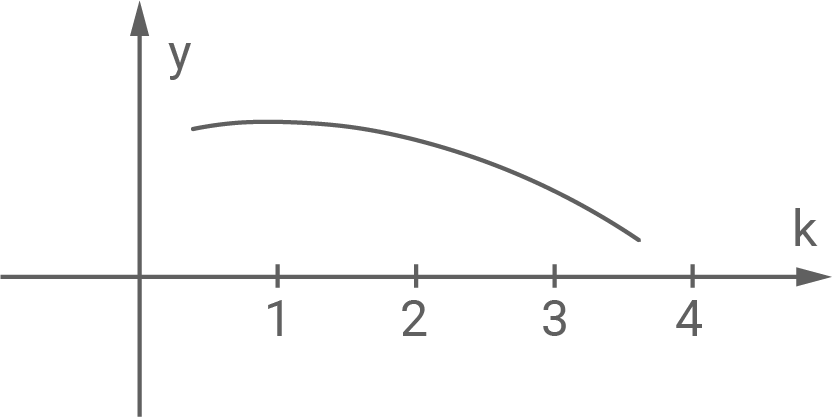
Es gibt eine Gerade $h,$ die in allen Ebenen der Schar liegt. Ermittle eine Gleichung von $h.$

$\left(\text{zur Kontrolle: } \overrightarrow{x}=\pmatrix{-4\\0\\2}+r \cdot\pmatrix{3\\1\\0}\right)$

(4 BE)

Begründe, dass $h$ parallel zur $x_1x_2$ -Ebene verläuft.

(1 BE)

Die Ebene $J$ enthält die Gerade $h,$ sie ist jedoch keine Ebene der Schar. Gib eine Gleichung von $J$ an.

(2 BE)

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?

Aufgabe II 1

Länge der kürzesten Kante berechnen

Aus der Abbildung wird deutlich, dass die Kante $\overline{AB}$ bzw. $\overline{AD}$ die kürzeste Kante der Pyramide ist. Somit folgt:

$\begin{array}[t]{rlll} \left\vert\overline{AB}\right\vert&=&\left\vert\pmatrix{2\\2\\0}-\pmatrix{0\\0\\0}\right\vert \\[5pt] &=&\sqrt{2^2+2^2+0^2} \\[5pt] &=&2\sqrt{2}\;[\text{LE}] \end{array}$

Volumen der Pyramide berechnen

Das Koordinatengitter in der Abbildung zeigt, dass die Grundfläche ein Drachenviereck mit Diagonalen der Länge $4\;\text{LE}$ und $6\;\text{LE}$ ist. Der Flächeninhalt $A$ der Grundfläche ist somit gegeben durch:

$\begin{array}[t]{rlll} A&=&\dfrac{1}{2}\cdot4\cdot6 \\[5pt] &=&12\;[\text{FE}] \end{array}$

Da die Grundfläche der Pyramide in der $x_1x_2$ -Ebene liegt, folgt aus den Koordinaten von $S,$ dass die Pyramide eine Höhe von $6\;\text{LE}$ besitzt. Damit ergibt sich für das Volumen $V$ der Pyramide:

$\begin{array}[t]{rlll} V&=&\dfrac{1}{3}\cdot12\cdot6 \\[5pt] &=&24\;[\text{VE}] \end{array}$

Für die Vektoren $\overrightarrow{BC}$ und $\overrightarrow{BS}$ gilt:

$\begin{array}[t]{rlll} \overrightarrow{BC}&=&\pmatrix{0\\6\\0}-\pmatrix{2\\2\\0} \\[5pt] &=&\pmatrix{-2\\4\\0} \\[5pt] &=&2\cdot\pmatrix{-1\\2\\0} \end{array}$

$\begin{array}[t]{rlll} \overrightarrow{BS}&=&\pmatrix{0\\0\\6}-\pmatrix{2\\2\\0} \\[5pt] &=&\pmatrix{-2\\-2\\6} \\[5pt] &=&2\cdot\pmatrix{-1\\-1\\3} \end{array}$

Die Vektoren $\overrightarrow{BC}$ und $\overrightarrow{BS}$ spannen die Ebene $E$ auf. Da sie zudem Vielfache der Vektoren aus der Aufgabenstellung sind, zu denen der Vektor $\pmatrix{n_1\\n_2\\n_3}$ orthogonal ist, folgt, dass dieser ein Normalenvektor der Ebene $E$ ist.

Ablesen des Normalenvektors $\overrightarrow{n}$ aus der Ebenengleichung von $E$ liefert:

$\overrightarrow{n}=\pmatrix{2\\1\\1}$

Somit folgt für den gesuchten Winkel:

$\begin{array}[t]{rlll} \cos(\alpha)&=&\dfrac{\left\vert\pmatrix{2\\1\\1}\circ\pmatrix{0\\0\\1}\right\vert}{\left\vert\pmatrix{2\\1\\1}\right\vert\cdot\left\vert\pmatrix{0\\0\\1}\right\vert} \\[5pt] \cos(\alpha)&=&\dfrac{1}{\sqrt{2^2+1^2+1^2}\cdot\sqrt{1^2}} \\[5pt] \cos(\alpha)&=&\dfrac{1}{\sqrt{6}} \\[5pt] \alpha&=&\cos^{-1}\left(\dfrac{1}{\sqrt{6}}\right) \\[5pt] \alpha&\approx&65,91^\circ \end{array}$

Gleichung von $\boldsymbol{F_2}$ angeben

$F_2:2x_2=4$

Schnittfigur einzeichnen

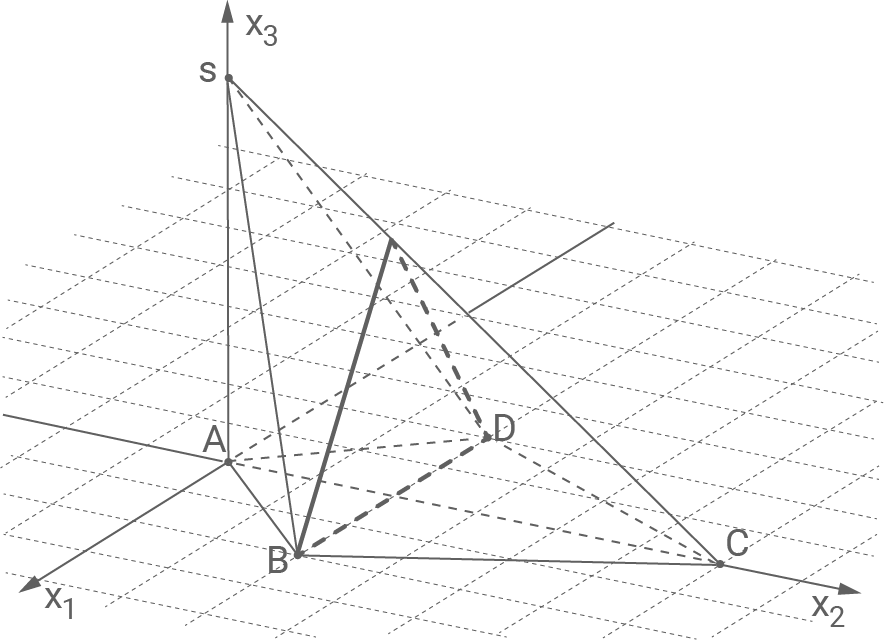
Die Dreiecke $BDQ_k$ sind alle gleichschenklig mit Grundseite $\overline{BD}.$ Der Flächeninhalt ist somit minimal, wenn die Höhe des Dreiecks, also der Abstand von $Q_k$ zum Mittelpunkt $M$ der Strecke $\overline{BD},$ am kleinsten ist. Da ist der Fall, wenn $\overline{MQ_k}$ senkrecht zur Kante $\overline{SC}$ steht, d.h. die Ebene $F_k$ senrecht zu dieser Kante steht. Der Normalenvektor dieser Ebene $F_k$ ist somit ein Vielfaches von $\overrightarrow{SC}:$

$\pmatrix{0\\k\\k-2}=\lambda\cdot\pmatrix{0\\6\\-6}$

Einsetzen der zweiten Zeile $k=6\lambda$ in die dritte Zeile liefert:

$\begin{array}[t]{rlll} k-2&=&-6\lambda \\[5pt] k-2&=&-k &\mid\;+k \\[5pt] 2k-2&=&0 &\mid\;+2 \\[5pt] 2k&=&2 &\mid\;:2 \\[5pt] k&=&1 \end{array}$

Der Flächeninhalt des Dreiecks $BDQ_k$ ist somit für $k=1$ minimal.

Aufgabe II 2

Mit Hilfe der Normalenvektoren der beiden Ebenen folgt:

Rechenweg anzeigen

$\alpha\approx17,55^\circ$

Aus den Vorfaktoren des $x_1$ - und $x_2$ -Terms der Ebene $F$ folgt, dass die Ebenengleichung von $F$ mit dem Faktor $2$ multipliziert werden muss, um in der Form der Schar $E_k$ zu sein. Durch die Vorfaktoren der $x_3$ -Terme folgt somit:

$\begin{array}[t]{rlll} -2&=&4-k &\mid\;+k \\[5pt] -2+k&=&4 &\mid\;+2 \\[5pt] k&=&6 \end{array}$

Mit Hilfe der Normalenvektoren der beiden Ebenen folgt:

$\begin{array}[t]{rlll} \pmatrix{1\\-3\\-1}\circ\pmatrix{2\\-6\\4-k}&=&0 \\[5pt] 2+18-(4-k)&=&0 &\mid\;-16 \\[5pt] k&=&-16 \end{array}$

Spurpunkte von $E_k$ bestimmen

Für die $x_1$ -Koordinate des Spurpunkts mit der $x_1$ -Achse folgt:

$\begin{array}[t]{rlll} 2x_1-6\cdot0+(4-k)\cdot0&=&-2k \\[5pt] 2x_1&=&-2k &\mid\;:2 \\[5pt] x_1&=&-k \end{array}$

Für die $x_2$ -Koordinate des Spurpunkts mit der $x_2$ -Achse folgt:

$\begin{array}[t]{rlll} 2\cdot0-6x_2+(4-k)\cdot0&=&-2k \\[5pt] -6x_2&=&-2k &\mid\;:(-6) \\[5pt] x_2&=&\dfrac{1}{3}k \end{array}$

Damit folgt für die Koordinaten der drei Eckpunkte des Dreiecks $(-k\mid0\mid0), \left(0\,\bigg\vert\,\frac{1}{3}k\,\bigg\vert\,0\right)$ und $\left(0\,\bigg\vert\,\frac{4}{3}\,\bigg\vert\,0\right).$

Aus den Koordinaten kann abgelesen werden, dass die Grundseite in der $x_1x_3$ -Ebene liegt. Die Höhe ergibt sich somit durch den Betrag der $x_1$ -Koordinate des ersten Eckpunkts. Für den Flächeninhalt des Dreiecks $D_k$ folgt damit:

$\begin{array}[t]{rlll} A(k)&=&\dfrac{1}{2}\cdot\left(\dfrac{4}{3}-\dfrac{1}{3}k\right)\cdot k \\[5pt] &=&-\dfrac{1}{6}k^2+\dfrac{2}{3}k \\[5pt] &=&-\dfrac{1}{6}\cdot(k-2)^2+\dfrac{2}{3} \end{array}$

Der Flächeninhalt des Dreiecks $D_k$ ist somit durch eine Parabel mit Scheitelpunkt bei $k=2$ gegeben. Damit stellt Graph I den Flächeninhalt von $D_k$ dar.

Mit Hilfe der Ebenengleichungen von z.B. $E_0$ und $E_4$ ergibt sich das folgende Gleichungssystem:

$\begin{array}{lrll} \text{I}\quad&2x_1-6x_2+4x_3&=&0 \\ \text{II}\quad&2x_1-6x_2&=&-8 \\ \end{array}$

Aus Gleichung $\text{II}$ folgt:

$\begin{array}[t]{rlll} 2x_1-6x_2&=&-8 &\mid\;+6x_2 \\[5pt] 2x_1&=&-8+6x_2 &\mid\;:2 \\[5pt] x_1&=&-4+3x_2 \end{array}$

Einsetzen in Gleichung $\text{I}$ liefert:

$\begin{array}[t]{rlll} 2\cdot(-4+3x_2)-6x_2+4x_3&=&0 \\[5pt] -8+4x_3&=&0 &\mid\;+8 \\[5pt] 4x_3&=&8 &\mid\;:4 \\[5pt] x_3&=&2 \end{array}$

Ersetzen von $x_2$ durch eine Variable $r$ liefert somit für die Form der Schnittpunkte:

$\pmatrix{3r-4\\r\\2}$

Damit folgt für die Geradengleichung von $h:$

$h:\overrightarrow{x}=\pmatrix{-4\\0\\2}+r\cdot\pmatrix{3\\1\\0}$

Die Gerade $h$ verläuft parallel zur $x_1 x_2$ -Ebene, da der Richtungsvektor von $h$ die $x_3$ -Koordinate $0$ hat.

Eine mögliche Ebenengleichung für $J$ ist durch $x_3=2$ gegeben, da der Normalenvektor nicht die Form der Normalenvektoren der Ebenenschar $E_k$ hat, und alle Punkte auf $h$ die $x_3$ -Koordinate $2$ besitzen.

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?