Prüfungsteil A: Ohne Hilfsmittel
Aufgabe 1: Analysis
Gegeben ist die Funktion
a)
Berechne 
(3 Punkte)
b)
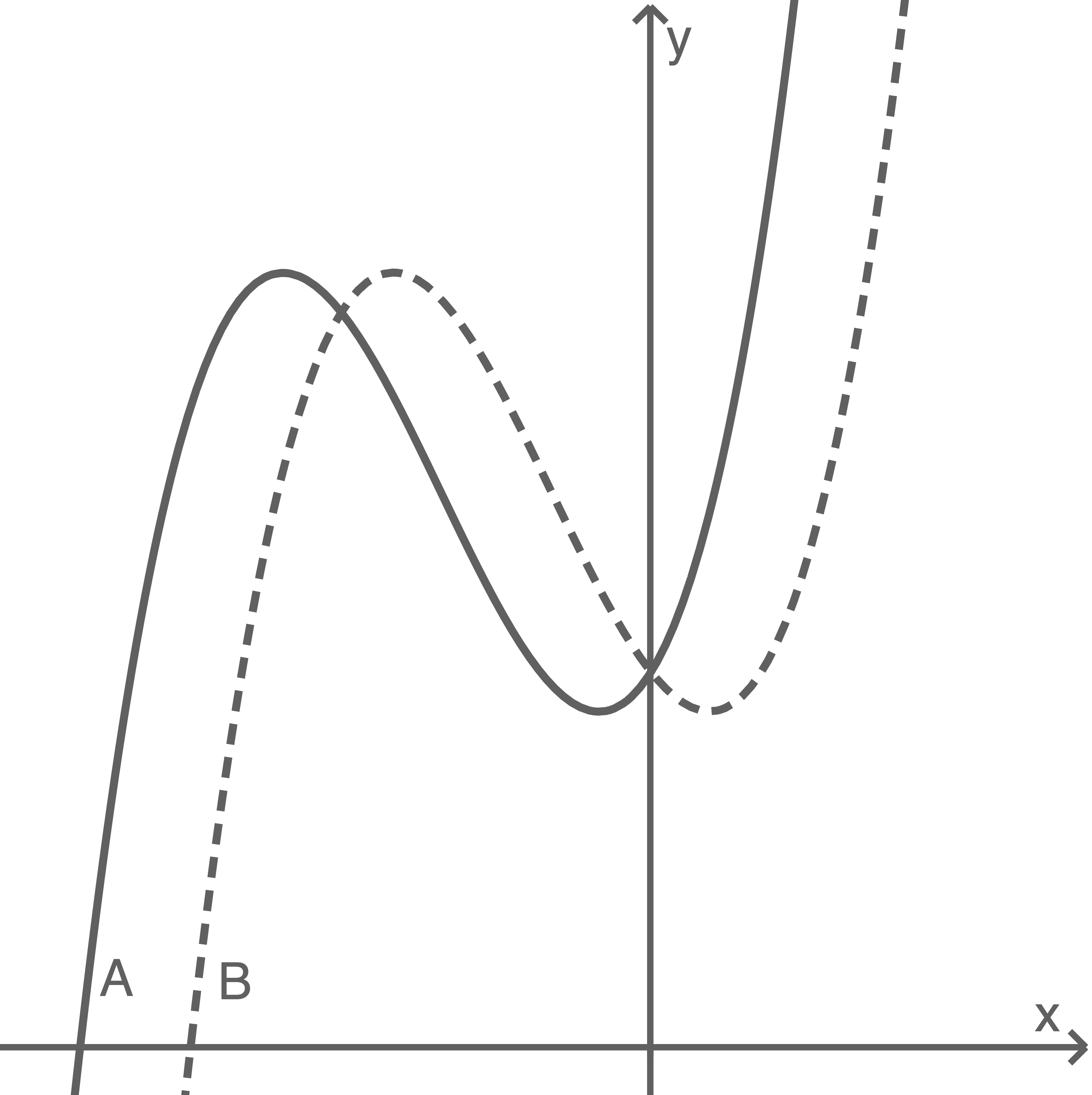
In der Abbildung sind zwei Graphen  und
und  abgebildet, einer davon ist der Graph der Funktion
abgebildet, einer davon ist der Graph der Funktion 
Für die Ableitung der Funktion an der Stelle
an der Stelle  gilt:
gilt: 
Entscheide mithilfe dieser Eigenschaft begründet, welcher der beiden Graphen der Graph von ist.
ist.
Für die Ableitung der Funktion
Entscheide mithilfe dieser Eigenschaft begründet, welcher der beiden Graphen der Graph von

Abbildung
(3 Punkte)
Aufgabe 2: Stochastik
In einem Land sind
a)
Stelle den oben beschriebenen Sachverhalt dar, indem du alle Prozentsätze in der folgenden Tabelle angibst.
| Nicht-Senioren | Senioren | Summe | |
|---|---|---|---|
| Nutzer | |||
| Nicht-Nutzer | |||
| Summe |
(4 Punkte)
b)
Eine Person nutzt das Internet.
Stelle einen Term für die Wahrscheinlichkeit auf, dass die Person ein Senior ist.
[Eine Berechnung der Wahrscheinlichkeit ist nicht erforderlich.]
Stelle einen Term für die Wahrscheinlichkeit auf, dass die Person ein Senior ist.
[Eine Berechnung der Wahrscheinlichkeit ist nicht erforderlich.]
(2 Punkte)
Lösung 1
a)
b)
Diese Bedingung erfüllt nur der Graph
Lösung 2
a)
| Nicht-Senior | Senior | Summe | |
|---|---|---|---|
| Nutzer | |||
| Nicht-Nutzer | |||
| Summe |
b)
Formel für die bedingte Wahrscheinlichkeit:

