Prüfungsteil B: Mit Hilfsmitteln
Aufgabe 3: Analysis (innermathematische Aufgabe)
Gegeben ist die Funktion  mit der Gleichung
mit der Gleichung  Die Abbildung 1 zeigt den Graphen von
Die Abbildung 1 zeigt den Graphen von 
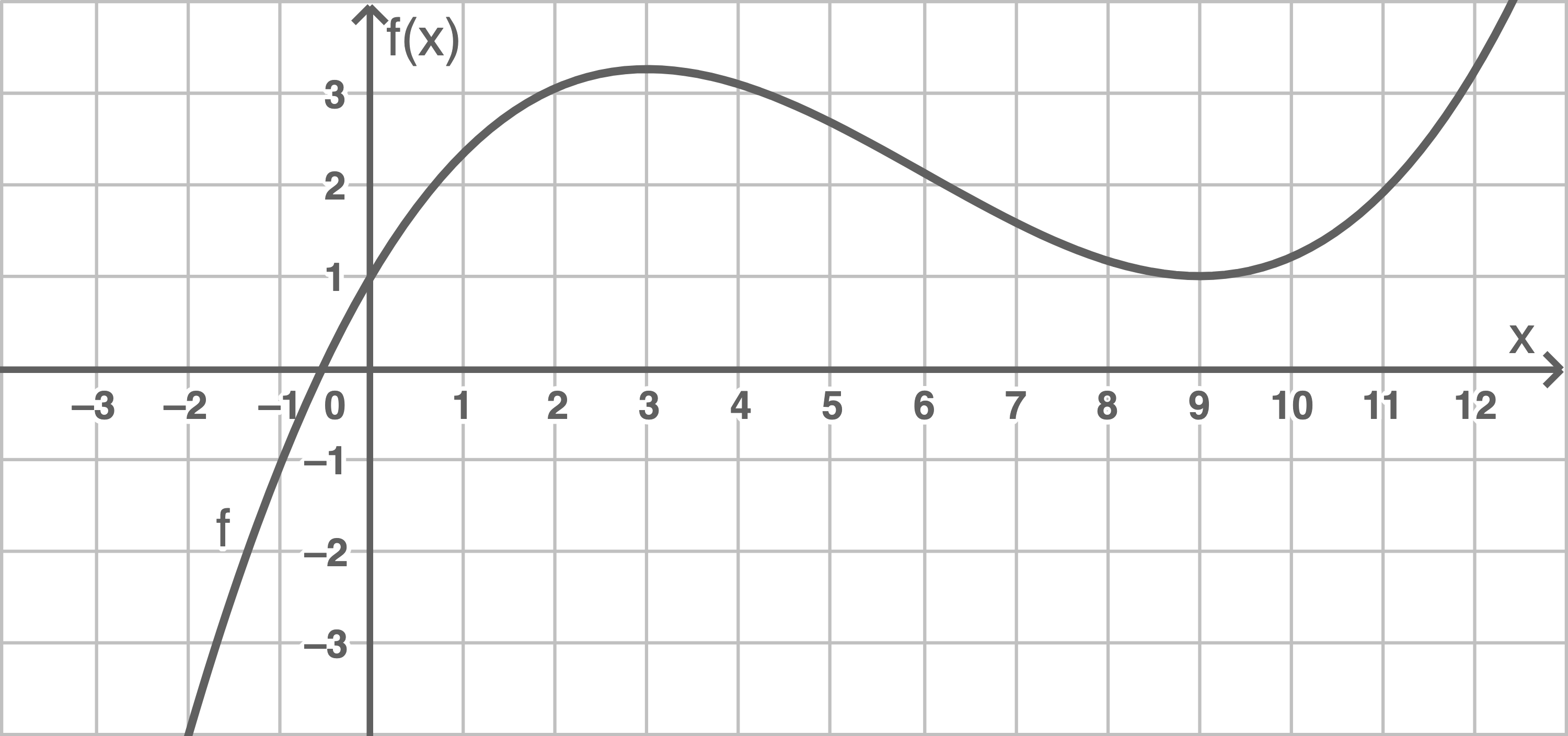
.png)

Abbildung 1
a)
(1)
Ermittle rechnerisch eine Gleichung der Geraden  durch die Punkte
durch die Punkte  und
und  [Zwischenergebnis: Die Gerade
[Zwischenergebnis: Die Gerade  hat die Steigung
hat die Steigung  .]
.]
(2)
Es gibt zwei Stellen, an denen der Graph von  Tangenten hat, die parallel zur Geraden
Tangenten hat, die parallel zur Geraden  verlaufen.
verlaufen.
Ermittle diese Stellen auf zwei Nachkommastellen genau.
Ermittle diese Stellen auf zwei Nachkommastellen genau.
(5+4 Punkte)
b)
Gegeben ist zusätzlich die Funktion  mit der Gleichung
mit der Gleichung

 geht durch eine Transformation aus dem Graphen der Funktion
geht durch eine Transformation aus dem Graphen der Funktion  hervor.
hervor.
(1)
Zeichne den Graphen von  in die Abbildung 1 ein.
in die Abbildung 1 ein.
Der Graph der Funktion
(2)
Gib diese Transformation an.
(3)
Gib eine Funktionsgleichung von  an, aus der die Transformation deutlich wird, durch die der Graph von
an, aus der die Transformation deutlich wird, durch die der Graph von  aus dem Graphen von
aus dem Graphen von  hervorgeht.
hervorgeht.
(4+2+2 Punkte)
c)
Die folgenden Abbildungen 2.1 bis 2.5 veranschaulichen, wie man den Wert der Ableitung  näherungsweise ermitteln kann.
näherungsweise ermitteln kann.
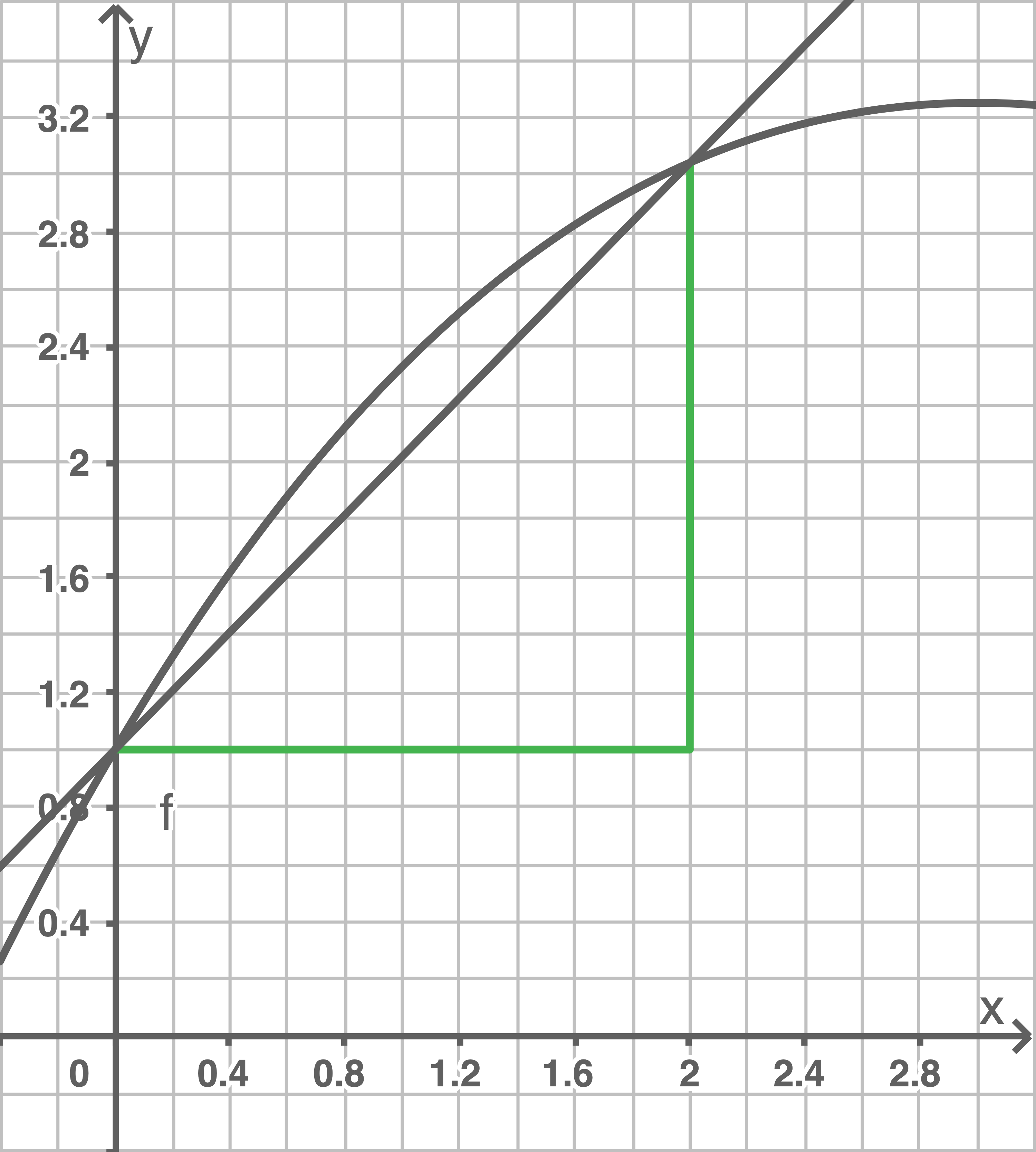
.png)
.png)

Abbildung 2.1
.png)
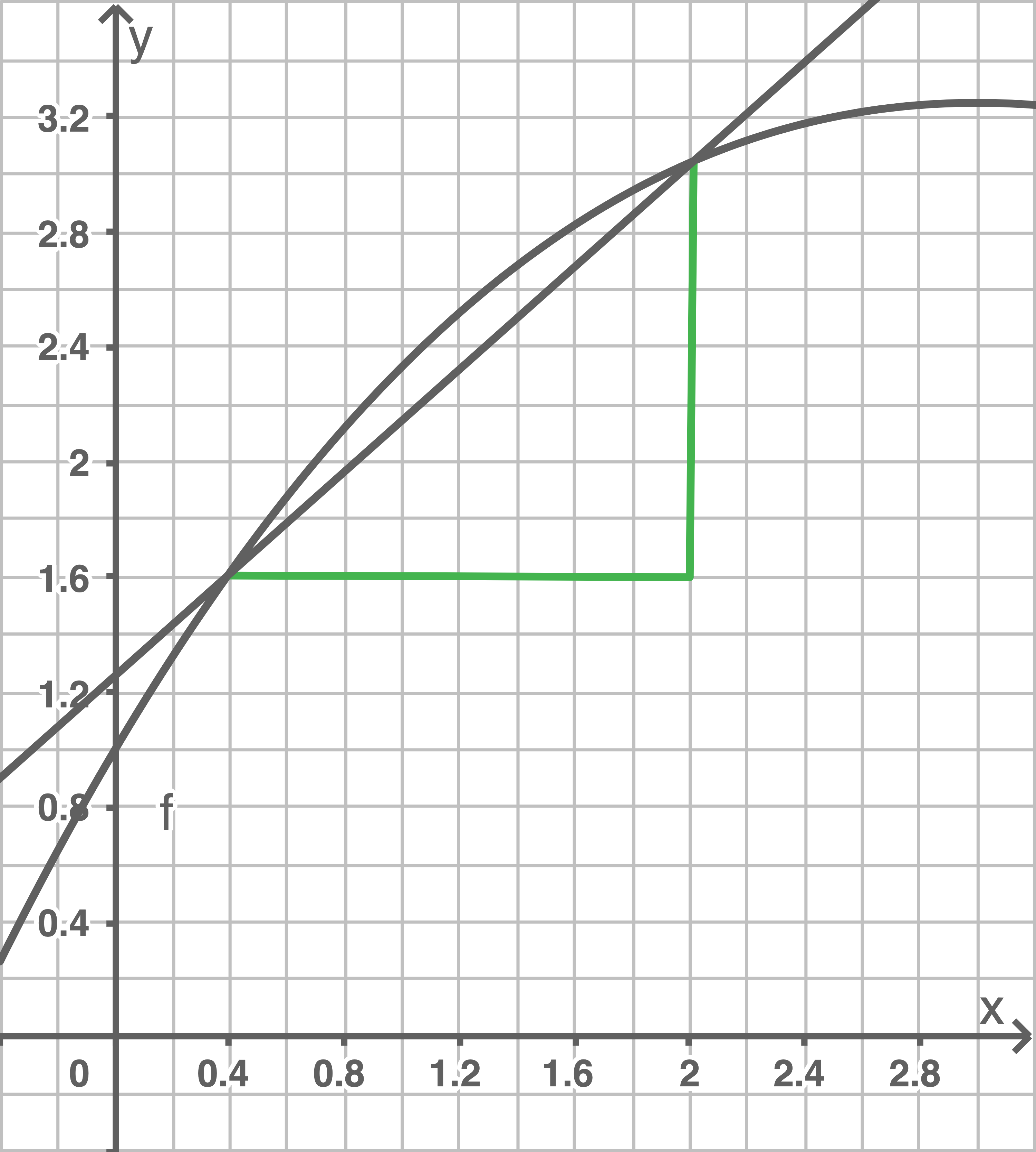
Abbildung 2.3

Abbildung 2.2
.png)
Abbildung 2.4
.png)
Abbildung 2.5
(1)
Gib an, welche Abbildung zum Differenzenquotienten  gehört.
gehört.
(2)
Gib an, welche geometrische Bedeutung der Wert  hat.
Erkläre, warum in den Abbildungen 2.1 bis 2.5 veranschaulicht wird, wie dieser Wert immer genauer ermittelt werden kann.
hat.
Erkläre, warum in den Abbildungen 2.1 bis 2.5 veranschaulicht wird, wie dieser Wert immer genauer ermittelt werden kann.
(2+5 Punkte)
Aufgabe 4: Analysis (kontextbezogene Aufgabe)
Während seines Urlaubs im norwegischen Vardø beobachtet Noah an einem Tag Anfang August die Sonne. Dabei misst er zu jeder vollen Stunde den Sonnenhöhenwinkel  (siehe Abbildung 1), um so zu bestimmen, wie hoch die Sonne über dem Horizont steht.
(siehe Abbildung 1), um so zu bestimmen, wie hoch die Sonne über dem Horizont steht.
Noah trägt seine Winkelmessungen in ein Koordinatensystem ein (siehe Abbildung 2).
Dabei entspricht der Uhrzeit 12:00 Uhr mittags,
der Uhrzeit 12:00 Uhr mittags,  entspricht 13:00 Uhr usw.
entspricht 13:00 Uhr usw.
Der Uhrzeit 11:00 Uhr entspricht usw.
usw.
Noah trägt seine Winkelmessungen in ein Koordinatensystem ein (siehe Abbildung 2).
Dabei entspricht
Der Uhrzeit 11:00 Uhr entspricht

Abbildung 1
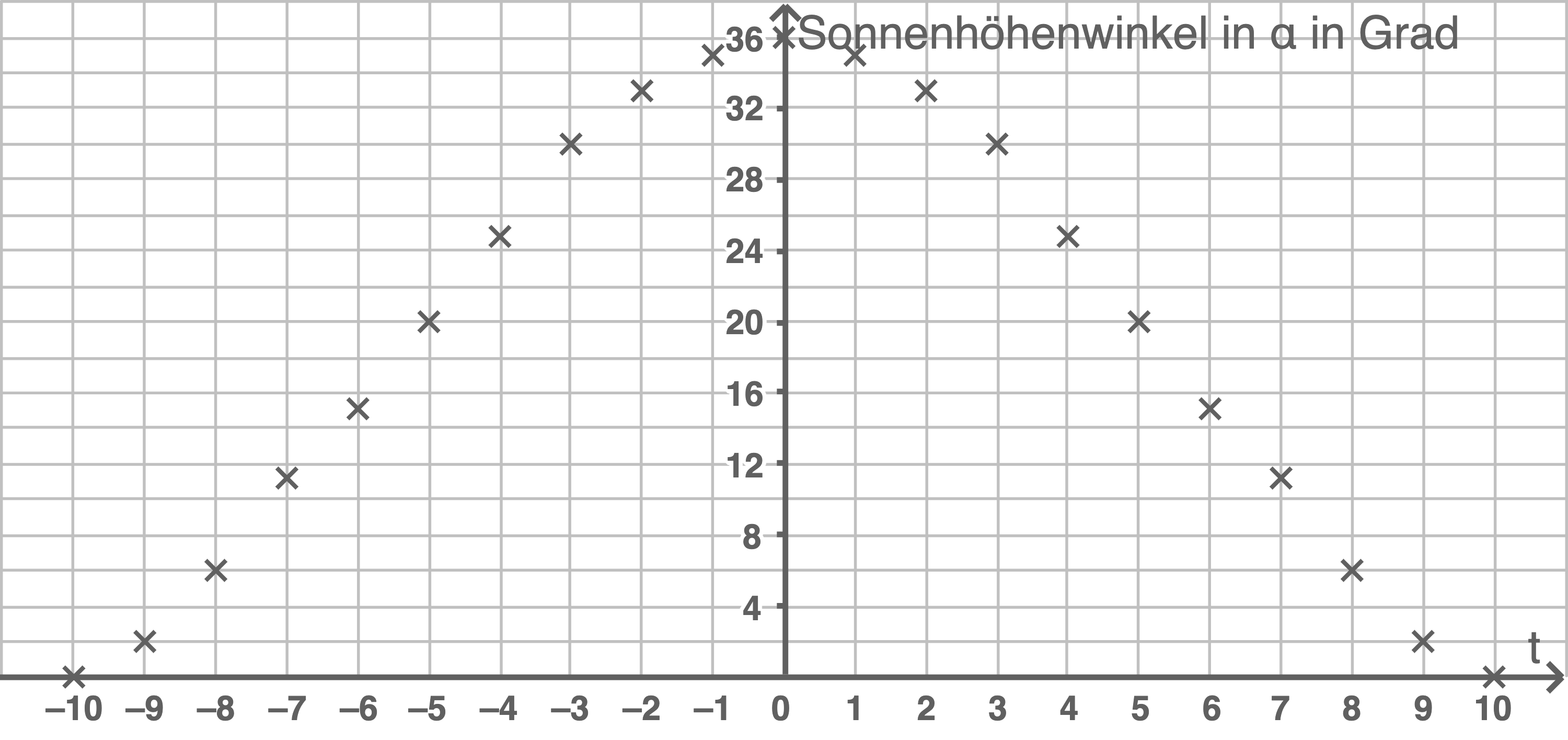
Abbildung 2
a)
(1) Gib den Sonnenhöhenwinkel an, den Noah um 7:00 Uhr morgens misst.
(2) Gib an, in welchem Zeitraum Noah Sonnenhöhenwinkel misst, die mindestens 30 Grad betragen.
Noah modelliert anhand seiner Daten den Sonnenhöhenwinkel im Laufe des Tages mit einer ganzrationalen Funktion 4. Grades. Er verwendet dazu für
(2+2 Punkte)
b)
Die Werte, die sich bei der Modellierung mit der Funktion  ergeben, weichen etwas von den Werten aus der Abbildung 2 ab.
Berechne die Abweichung zwischen dem um 7:00 Uhr morgens gemessenen Wert und dem entsprechenden Funktionswert.
ergeben, weichen etwas von den Werten aus der Abbildung 2 ab.
Berechne die Abweichung zwischen dem um 7:00 Uhr morgens gemessenen Wert und dem entsprechenden Funktionswert.
(2 Punkte)
c)
Bei der Messung von Noah erreicht die Sonne ihren höchsten Stand um 12:00 Uhr mittags (siehe Abbildung 2).
Weise rechnerisch nach, dass auch bei der Modellierung mit der Funktion  die Sonne zu diesem Zeitpunkt ihren höchsten Stand erreicht.
die Sonne zu diesem Zeitpunkt ihren höchsten Stand erreicht.
(7 Punkte)
d)
(1) Weise nach, dass gilt:  .
(2) Interpretiere diese Ungleichung im Sachzusammenhang.
.
(2) Interpretiere diese Ungleichung im Sachzusammenhang.
An einem Tag Ende August beobachtet Noah noch einmal die Sonne in Vardø. Um 04:00 Uhr morgens während des Sonnenaufgangs misst er den Sonnenhöhenwinkel 0 Grad, um 12:00 Uhr mittags ist der Sonnenhöhenwinkel mit 29 Grad maximal.
(2+2 Punkte)
Noah möchte für diesen Tag den Sonnenhöhenwinkel mit einer ganzrationalen Funktion
e)
(1)
Skizziere in der Abbildung 2 den Verlauf eines möglichen Graphen von  .
.
(2)
Für die Funktionsgleichung von  wählt Noah den Ansatz:
wählt Noah den Ansatz:  Ermittle für
Ermittle für  und
und  jeweils einen zu seiner Messung passenden Wert.
jeweils einen zu seiner Messung passenden Wert.
(3+4 Punkte)
Lösung 3
a)
(1)
1. Schritt: Steigung berechnen
![\(\begin{array}[t]{rll}
m&=&\dfrac{y_T-y_H}{x_T-x_H} &\quad \\[5pt]
m&=&\dfrac{1-\frac{13}{4}}{9-3} &\quad \\[5pt]
&=& -\dfrac{3}{8}
\end{array}\)](https://www.schullv.de/resources/formulas/52992d7c5ba647a4271de8350d56c6d03cebae31abcd6b5021d78ba6487fd8b4_light.svg) 2. Schritt:
2. Schritt:  und
und  in die Geradengleichung einsetzen
in die Geradengleichung einsetzen
![\(\begin{array}[t]{rll}
y&=& m \cdot x + t &\quad \\[5pt]
1&=& -\dfrac{3}{8} \cdot 9 + t &\quad \\[5pt]
1&=&-\dfrac{27}{8} + t \quad \scriptsize \mid\; +\dfrac {27}{8} \\[5pt]
\dfrac{35}{8} &=& t
\end{array}\)](https://www.schullv.de/resources/formulas/18c79f95d1191aa468c876981a248fc9cff261884d2e31e50d3541a4efafe62f_light.svg) Die Geradengleichung lautet also wie folgt:
Die Geradengleichung lautet also wie folgt:

(2)
Die Tangenten sollen parallel zur Geraden verlaufen, daher müssen sie die gleiche Steigung wie die Gerade  besitzen, also
besitzen, also  1. Schritt:
1. Schritt:  ableiten
ableiten
![\(\begin{array}[t]{rll}
f(x)&=&\dfrac{1}{48}\cdot x^3 - \dfrac{3}{8} \cdot x^2 + \dfrac{27}{16} \cdot x + 1 &\quad \\[5pt]
f](https://www.schullv.de/resources/formulas/ae111588166fe41a6450e9223450b6791b3e4173d736cfeb66729e2daf1d68db_light.svg) 2. Schritt: Schnittpunkte berechnen
Werden die Funktion
2. Schritt: Schnittpunkte berechnen
Werden die Funktion  und die Steigung
und die Steigung  im CAS definiert, lassen sich die Schnittpunkte wie folgt berechnen.
im CAS definiert, lassen sich die Schnittpunkte wie folgt berechnen.
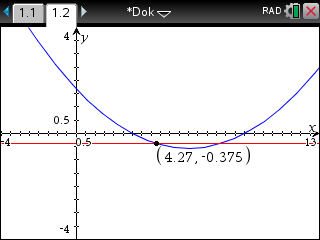 Schnittpunkt 1
Schnittpunkt 1
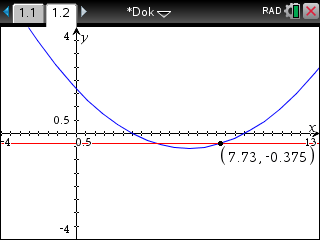 Schnittpunkt 2
Die Stellen, an denen der Graph von
Schnittpunkt 2
Die Stellen, an denen der Graph von  Tangenten hat, die parallel zur Geraden
Tangenten hat, die parallel zur Geraden  verlaufen sind
verlaufen sind  und
und 
menu  6: Graph analysieren
6: Graph analysieren  4: Schnittpunkt
4: Schnittpunkt
 Schnittpunkt 1
Schnittpunkt 1
 Schnittpunkt 2
Schnittpunkt 2
b)
(1)
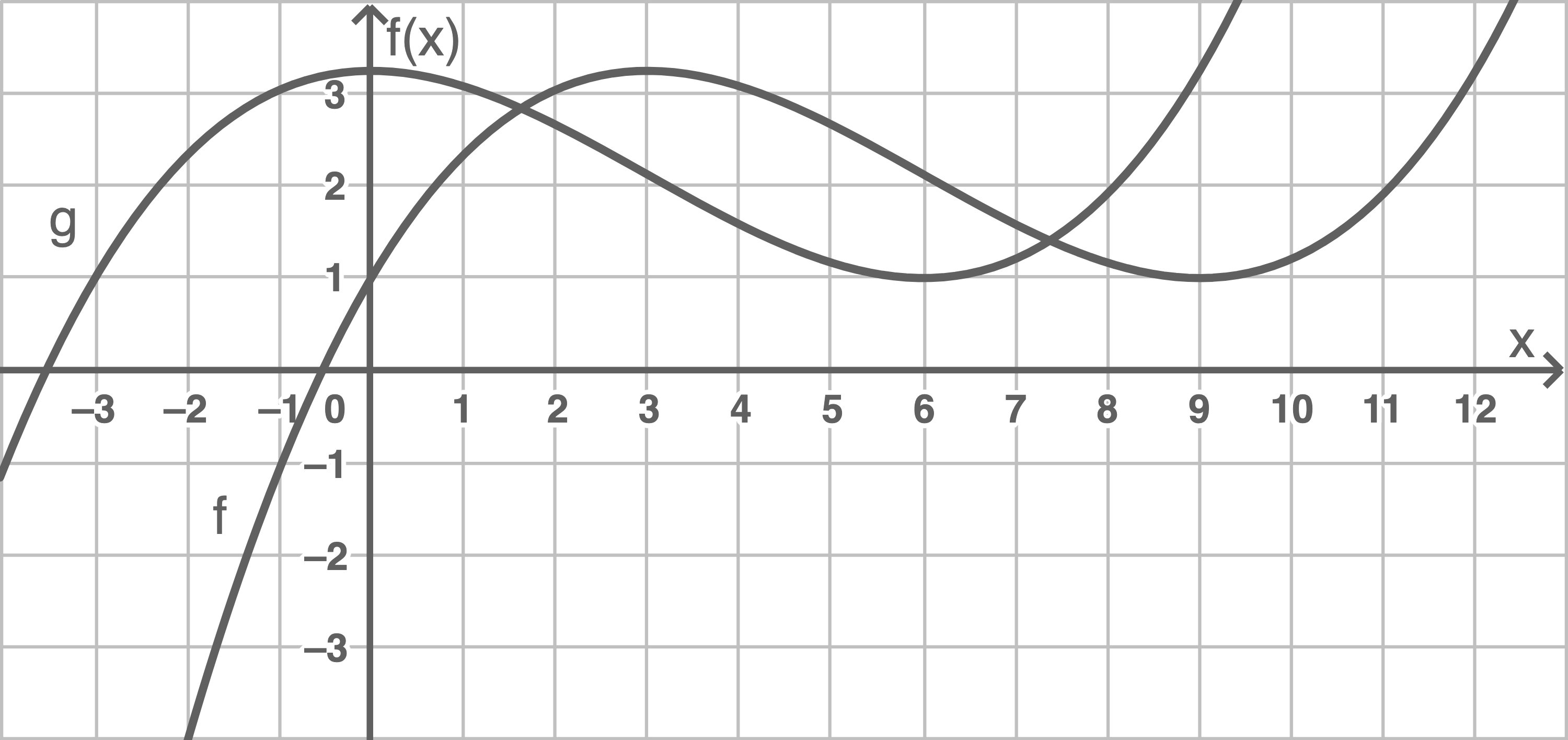
Graph von 
(2)
Koordinaten der Extrempunkte vergleichen, um genaue Transformation anzugeben:
 liegt bei
liegt bei  , der Hochpunkt von
, der Hochpunkt von  liegt bei
liegt bei  .
Der Tiefpunkt von
.
Der Tiefpunkt von  liegt bei
liegt bei  , der Tiefpunkt von
, der Tiefpunkt von  liegt bei
liegt bei  .
Der Graph von
.
Der Graph von  geht also aus dem Graphen von
geht also aus dem Graphen von  hervor, indem der Graph von
hervor, indem der Graph von  um
um  Einheiten in negative
Einheiten in negative  -Richtung verschoben wird.
-Richtung verschoben wird.
menu  6: Graph analysieren
6: Graph analysieren  3: Maximum
3: Maximum
Der Hochpunkt von
(3)
c)
(1)
Allgemeine Formel des Differenzquotienten:  Der Punkt
Der Punkt  ist in jeder Abbildung ein Eckpunkt des Steigungsdreiecks. Der zweite Eckunkt ist im vorgegebenen Differenzenquotienten
ist in jeder Abbildung ein Eckpunkt des Steigungsdreiecks. Der zweite Eckunkt ist im vorgegebenen Differenzenquotienten  durch
durch  gegeben. Der Differenzenquotient gehört daher zu Abbildung 2.3.
gegeben. Der Differenzenquotient gehört daher zu Abbildung 2.3.
(2)
Lösung 4
a)
(1)
Da 12:00 Uhr  entspricht, gilt für 7:00 Uhr morgens
entspricht, gilt für 7:00 Uhr morgens  Ablesen des
Ablesen des  -Werts bei
-Werts bei  aus Abbildung 2 zeigt, dass der Sonnenhöhenwinkel um 7:00 Uhr morgens
aus Abbildung 2 zeigt, dass der Sonnenhöhenwinkel um 7:00 Uhr morgens  beträgt.
beträgt.
(2)
Der Sonnenhöhenwinkel liegt zwischen  und
und  bei mindestens
bei mindestens 
 entspricht der Uhrzeit 9:00 Uhr und
entspricht der Uhrzeit 9:00 Uhr und  der Uhrzeit 15:00 Uhr.
der Uhrzeit 15:00 Uhr.
Folglich misst Noah im Zeitraum von 9:00 - 15:00 Uhr Sonnenhöhenwinkel, die mindestens betragen.
betragen.
Folglich misst Noah im Zeitraum von 9:00 - 15:00 Uhr Sonnenhöhenwinkel, die mindestens
b)
Graphen der Funktion im CAS aufzeichnen lassen und den  -Wert zu
-Wert zu  berechnen lassen:
berechnen lassen:
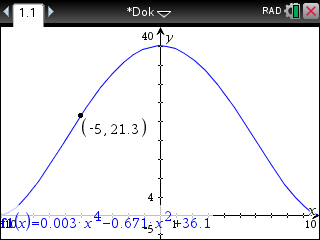
 -Wert zum Zeitpunkt
-Wert zum Zeitpunkt 
 Bei der Modellierung der Funktion liegt der Sonnenhöhenwinkel bei
Bei der Modellierung der Funktion liegt der Sonnenhöhenwinkel bei  statt bei
statt bei  . Der Funktionswert weicht also um
. Der Funktionswert weicht also um  vom gemessenen Wert ab.
vom gemessenen Wert ab.
menu  8: Geometry
8: Geometry  1: Punkte und Geraden
1: Punkte und Geraden  1: Punkt
1: Punkt

c)
1. Schritt:  ableiten
ableiten
![\(\begin{array}[t]{rll}
f(t) &=& 0,0031\cdot t^4-0,671 \cdot t^2+36,1&\quad \scriptsize \\[5pt]
f](https://www.schullv.de/resources/formulas/737d1e75bc252e5452c7198b5a0a2334e9bfe7e22d55bd8950e1a4589628cdfd_light.svg) 2. Schritt: Notwendige Bedingung anwenden
Da
2. Schritt: Notwendige Bedingung anwenden
Da  und
und  bei
bei  nicht im Zeitraum der Messungen liegen, wird nur mit
nicht im Zeitraum der Messungen liegen, wird nur mit  weitergerechnet.
3. Schritt: Vorzeichenwechsel-Kriterium prüfen
weitergerechnet.
3. Schritt: Vorzeichenwechsel-Kriterium prüfen

 An der Stelle
An der Stelle  liegt also ein Vorzeichenwechsel der Ableitung von + nach - und somit ein lokales Maximum von
liegt also ein Vorzeichenwechsel der Ableitung von + nach - und somit ein lokales Maximum von  vor. Überprüfen der Randwerte liefert:
vor. Überprüfen der Randwerte liefert:
 Somit liegt an der Stelle
Somit liegt an der Stelle  ein absolutes Maximum vor. Da
ein absolutes Maximum vor. Da  den Sonnenhöhenwinkel um 12:00 Uhr beschreibt, gilt für die Modellierung der Funktion
den Sonnenhöhenwinkel um 12:00 Uhr beschreibt, gilt für die Modellierung der Funktion  dass sie an dieser Stelle ihren höchsten Stand erreicht.
dass sie an dieser Stelle ihren höchsten Stand erreicht.
d)
(1)
Beide Werte für  in die erste Ableitung einsetzen und ausrechnen:
in die erste Ableitung einsetzen und ausrechnen:
![\(\begin{array}[t]{rll}
f](https://www.schullv.de/resources/formulas/ebbe07628e16298ff5f3262d87e6093a298bb96aec7dc0101a8468bfddc42052_light.svg) Es ist
Es ist  daher stimmt die Aussage.
daher stimmt die Aussage.
(2)
Die Ableitungen an den Stellen  und
und  beschreiben die Steigung des Graphen der Funktion
beschreiben die Steigung des Graphen der Funktion  an diesen Stellen.
an diesen Stellen.
Zum Zeitpunkt steigt die Funktion
steigt die Funktion  stärker als zum Zeitpunkt
stärker als zum Zeitpunkt  also nimmt der Sonnenhöhenwinkel um 3:00 Uhr
also nimmt der Sonnenhöhenwinkel um 3:00 Uhr  schneller zu als um 10:00 Uhr
schneller zu als um 10:00 Uhr 
Zum Zeitpunkt
e)
(1)
Skizze mit Hilfe markanter Punkte erstellen, bspw. mit den Koordinaten des Hochpunkts  und der Nullstellen
und der Nullstellen  und
und 
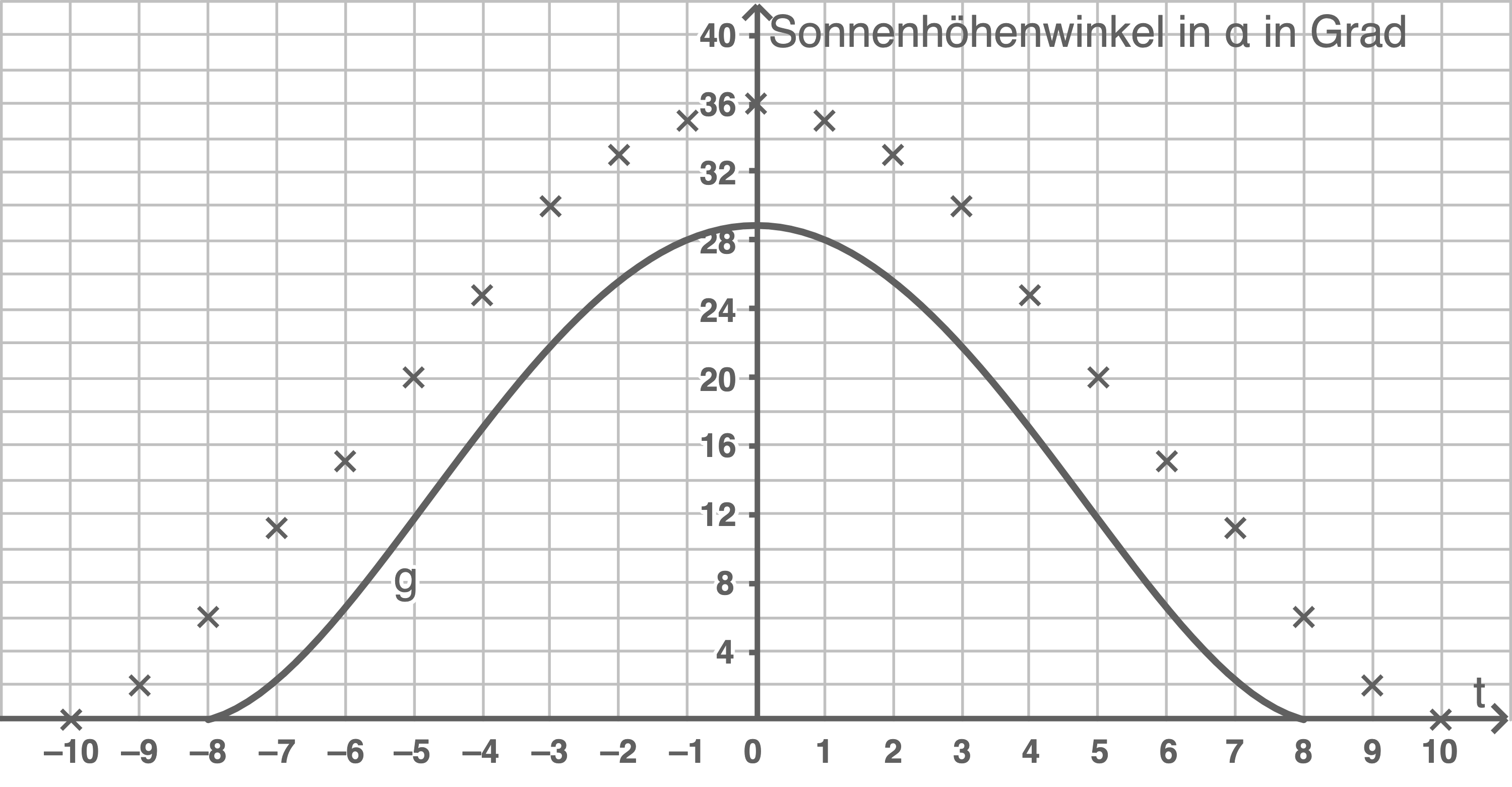

Graph von 
(2)
Wert  bestimmen
Der Wert
bestimmen
Der Wert  stellt den Stauchungsfaktor in
stellt den Stauchungsfaktor in  -Richtung dar. Er kann durch das Verhältnis der Funktionswerte bei
-Richtung dar. Er kann durch das Verhältnis der Funktionswerte bei  berechnet werden:
Die Funktion wird also um den Faktor
berechnet werden:
Die Funktion wird also um den Faktor  in
in  -Richtung gestaucht.
Wert
-Richtung gestaucht.
Wert  bestimmen
Analog kann durch Betrachtung der Nullstellen die Stauchung der Funktion in
bestimmen
Analog kann durch Betrachtung der Nullstellen die Stauchung der Funktion in  -Richtung bestimmt werden.
Die Funktion wird also um den Faktor
-Richtung bestimmt werden.
Die Funktion wird also um den Faktor  in
in  -Richtung gestaucht.
Funktionsgleichung aufstellen
-Richtung gestaucht.
Funktionsgleichung aufstellen

Lösung 3
a)
(1)
1. Schritt: Steigung berechnen
![\(\begin{array}[t]{rll}
m&=&\dfrac{y_T-y_H}{x_T-x_H} &\quad \\[5pt]
m&=&\dfrac{1-\frac{13}{4}}{9-3} &\quad \\[5pt]
&=& -\dfrac{3}{8}
\end{array}\)](https://www.schullv.de/resources/formulas/52992d7c5ba647a4271de8350d56c6d03cebae31abcd6b5021d78ba6487fd8b4_light.svg) 2. Schritt:
2. Schritt:  und
und  in die Geradengleichung einsetzen
in die Geradengleichung einsetzen
![\(\begin{array}[t]{rll}
y&=& m \cdot x + t &\quad \\[5pt]
1&=& -\dfrac{3}{8} \cdot 9 + t &\quad \\[5pt]
1&=&-\dfrac{27}{8} + t \quad \scriptsize \mid\; +\dfrac {27}{8} \\[5pt]
\dfrac{35}{8} &=& t
\end{array}\)](https://www.schullv.de/resources/formulas/18c79f95d1191aa468c876981a248fc9cff261884d2e31e50d3541a4efafe62f_light.svg) Die Geradengleichung lautet also wie folgt:
Die Geradengleichung lautet also wie folgt:

(2)
Die Tangenten sollen parallel zur Geraden verlaufen, daher müssen sie die gleiche Steigung wie die Gerade  besitzen, also
besitzen, also  1. Schritt:
1. Schritt:  ableiten
ableiten
![\(\begin{array}[t]{rll}
f(x)&=&\dfrac{1}{48}\cdot x^3 - \dfrac{3}{8} \cdot x^2 + \dfrac{27}{16} \cdot x + 1 &\quad \\[5pt]
f](https://www.schullv.de/resources/formulas/ae111588166fe41a6450e9223450b6791b3e4173d736cfeb66729e2daf1d68db_light.svg) 2. Schritt: Schnittpunkte berechnen
Werden die Funktion
2. Schritt: Schnittpunkte berechnen
Werden die Funktion  und die Steigung
und die Steigung  im CAS definiert, lassen sich die Schnittpunkte wie folgt berechnen.
im CAS definiert, lassen sich die Schnittpunkte wie folgt berechnen.
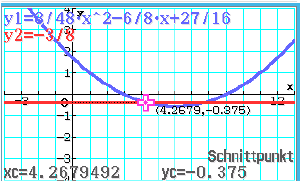 Schnittpunkt 1
Schnittpunkt 1
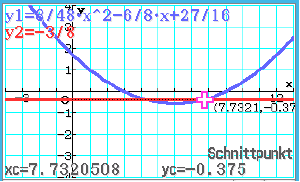 Schnittpunkt 2
Die Stellen, an denen der Graph von
Schnittpunkt 2
Die Stellen, an denen der Graph von  Tangenten hat, die parallel zur Geraden
Tangenten hat, die parallel zur Geraden  verlaufen sind
verlaufen sind  und
und 
Analyse  Grafische Lösung
Grafische Lösung  Schnittpunkt
Schnittpunkt
 Schnittpunkt 1
Schnittpunkt 1
 Schnittpunkt 2
Schnittpunkt 2
b)
(1)

Graph von 
(2)
Koordinaten der Extrempunkte vergleichen, um genaue Transformation anzugeben:
 liegt bei
liegt bei  , der Hochpunkt von
, der Hochpunkt von  liegt bei
liegt bei  .
Der Tiefpunkt von
.
Der Tiefpunkt von  liegt bei
liegt bei  , der Tiefpunkt von
, der Tiefpunkt von  liegt bei
liegt bei  .
Der Graph von
.
Der Graph von  geht also aus dem Graphen von
geht also aus dem Graphen von  hervor, indem der Graph von
hervor, indem der Graph von  um
um  Einheiten in negative
Einheiten in negative  -Richtung verschoben wird.
-Richtung verschoben wird.
Analyse  Grafische Lösung
Grafische Lösung  Maximum
Maximum
Der Hochpunkt von
(3)
c)
(1)
Allgemeine Formel des Differenzquotienten:  Der Punkt
Der Punkt  ist in jeder Abbildung ein Eckpunkt des Steigungsdreiecks. Der zweite Eckunkt ist im vorgegebenen Differenzenquotienten
ist in jeder Abbildung ein Eckpunkt des Steigungsdreiecks. Der zweite Eckunkt ist im vorgegebenen Differenzenquotienten  durch
durch  gegeben. Der Differenzenquotient gehört daher zu Abbildung 2.3.
gegeben. Der Differenzenquotient gehört daher zu Abbildung 2.3.
(2)
Lösung 4
a)
(1)
Da 12:00 Uhr  entspricht, gilt für 7:00 Uhr morgens
entspricht, gilt für 7:00 Uhr morgens  Ablesen des
Ablesen des  -Werts bei
-Werts bei  aus Abbildung 2 zeigt, dass der Sonnenhöhenwinkel um 7:00 Uhr morgens
aus Abbildung 2 zeigt, dass der Sonnenhöhenwinkel um 7:00 Uhr morgens  beträgt.
beträgt.
(2)
Der Sonnenhöhenwinkel liegt zwischen  und
und  bei mindestens
bei mindestens 
 entspricht der Uhrzeit 9:00 Uhr und
entspricht der Uhrzeit 9:00 Uhr und  der Uhrzeit 15:00 Uhr.
der Uhrzeit 15:00 Uhr.
Folglich misst Noah im Zeitraum von 9:00 - 15:00 Uhr Sonnenhöhenwinkel, die mindestens betragen.
betragen.
Folglich misst Noah im Zeitraum von 9:00 - 15:00 Uhr Sonnenhöhenwinkel, die mindestens
b)
Graphen der Funktion im CAS aufzeichnen lassen und den  -Wert zu
-Wert zu  berechnen lassen:
berechnen lassen:
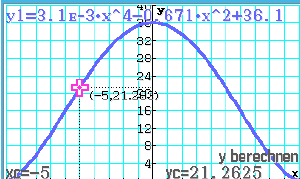
 -Wert zum Zeitpunkt
-Wert zum Zeitpunkt 
 Bei der Modellierung der Funktion liegt der Sonnenhöhenwinkel bei
Bei der Modellierung der Funktion liegt der Sonnenhöhenwinkel bei  statt bei
statt bei  . Der Funktionswert weicht also um
. Der Funktionswert weicht also um  vom gemessenen Wert ab.
vom gemessenen Wert ab.
Analyse  Grafische Lösung
Grafische Lösung  x/y-Berech.
x/y-Berech.  y berechnen
y berechnen

c)
1. Schritt:  ableiten
ableiten
![\(\begin{array}[t]{rll}
f(t) &=& 0,0031\cdot t^4-0,671 \cdot t^2+36,1&\quad \scriptsize \\[5pt]
f](https://www.schullv.de/resources/formulas/737d1e75bc252e5452c7198b5a0a2334e9bfe7e22d55bd8950e1a4589628cdfd_light.svg) 2. Schritt: Notwendige Bedingung anwenden
Da
2. Schritt: Notwendige Bedingung anwenden
Da  und
und  bei
bei  nicht im Zeitraum der Messungen liegen, wird nur mit
nicht im Zeitraum der Messungen liegen, wird nur mit  weitergerechnet.
3. Schritt: Vorzeichenwechsel-Kriterium prüfen
weitergerechnet.
3. Schritt: Vorzeichenwechsel-Kriterium prüfen

 An der Stelle
An der Stelle  liegt also ein Vorzeichenwechsel der Ableitung von + nach - und somit ein lokales Maximum von
liegt also ein Vorzeichenwechsel der Ableitung von + nach - und somit ein lokales Maximum von  vor. Überprüfen der Randwerte liefert:
vor. Überprüfen der Randwerte liefert:
 Somit liegt an der Stelle
Somit liegt an der Stelle  ein absolutes Maximum vor. Da
ein absolutes Maximum vor. Da  den Sonnenhöhenwinkel um 12:00 Uhr beschreibt, gilt für die Modellierung der Funktion
den Sonnenhöhenwinkel um 12:00 Uhr beschreibt, gilt für die Modellierung der Funktion  dass sie an dieser Stelle ihren höchsten Stand erreicht.
dass sie an dieser Stelle ihren höchsten Stand erreicht.
d)
(1)
Beide Werte für  in die erste Ableitung einsetzen und ausrechnen:
in die erste Ableitung einsetzen und ausrechnen:
![\(\begin{array}[t]{rll}
f](https://www.schullv.de/resources/formulas/ebbe07628e16298ff5f3262d87e6093a298bb96aec7dc0101a8468bfddc42052_light.svg) Es ist
Es ist  daher stimmt die Aussage.
daher stimmt die Aussage.
(2)
Die Ableitungen an den Stellen  und
und  beschreiben die Steigung des Graphen der Funktion
beschreiben die Steigung des Graphen der Funktion  an diesen Stellen.
an diesen Stellen.
Zum Zeitpunkt steigt die Funktion
steigt die Funktion  stärker als zum Zeitpunkt
stärker als zum Zeitpunkt  also nimmt der Sonnenhöhenwinkel um 3:00 Uhr
also nimmt der Sonnenhöhenwinkel um 3:00 Uhr  schneller zu als um 10:00 Uhr
schneller zu als um 10:00 Uhr 
Zum Zeitpunkt
e)
(1)
Skizze mit Hilfe markanter Punkte erstellen, bspw. mit den Koordinaten des Hochpunkts  und der Nullstellen
und der Nullstellen  und
und 


Graph von 
(2)
Wert  bestimmen
Der Wert
bestimmen
Der Wert  stellt den Stauchungsfaktor in
stellt den Stauchungsfaktor in  -Richtung dar. Er kann durch das Verhältnis der Funktionswerte bei
-Richtung dar. Er kann durch das Verhältnis der Funktionswerte bei  berechnet werden:
Die Funktion wird also um den Faktor
berechnet werden:
Die Funktion wird also um den Faktor  in
in  -Richtung gestaucht.
Wert
-Richtung gestaucht.
Wert  bestimmen
Analog kann durch Betrachtung der Nullstellen die Stauchung der Funktion in
bestimmen
Analog kann durch Betrachtung der Nullstellen die Stauchung der Funktion in  -Richtung bestimmt werden.
Die Funktion wird also um den Faktor
-Richtung bestimmt werden.
Die Funktion wird also um den Faktor  in
in  -Richtung gestaucht.
Funktionsgleichung aufstellen
-Richtung gestaucht.
Funktionsgleichung aufstellen
