Prüfungsteil A: Ohne Hilfsmittel
Aufgabe 1: Analysis
Gegeben ist die Funktion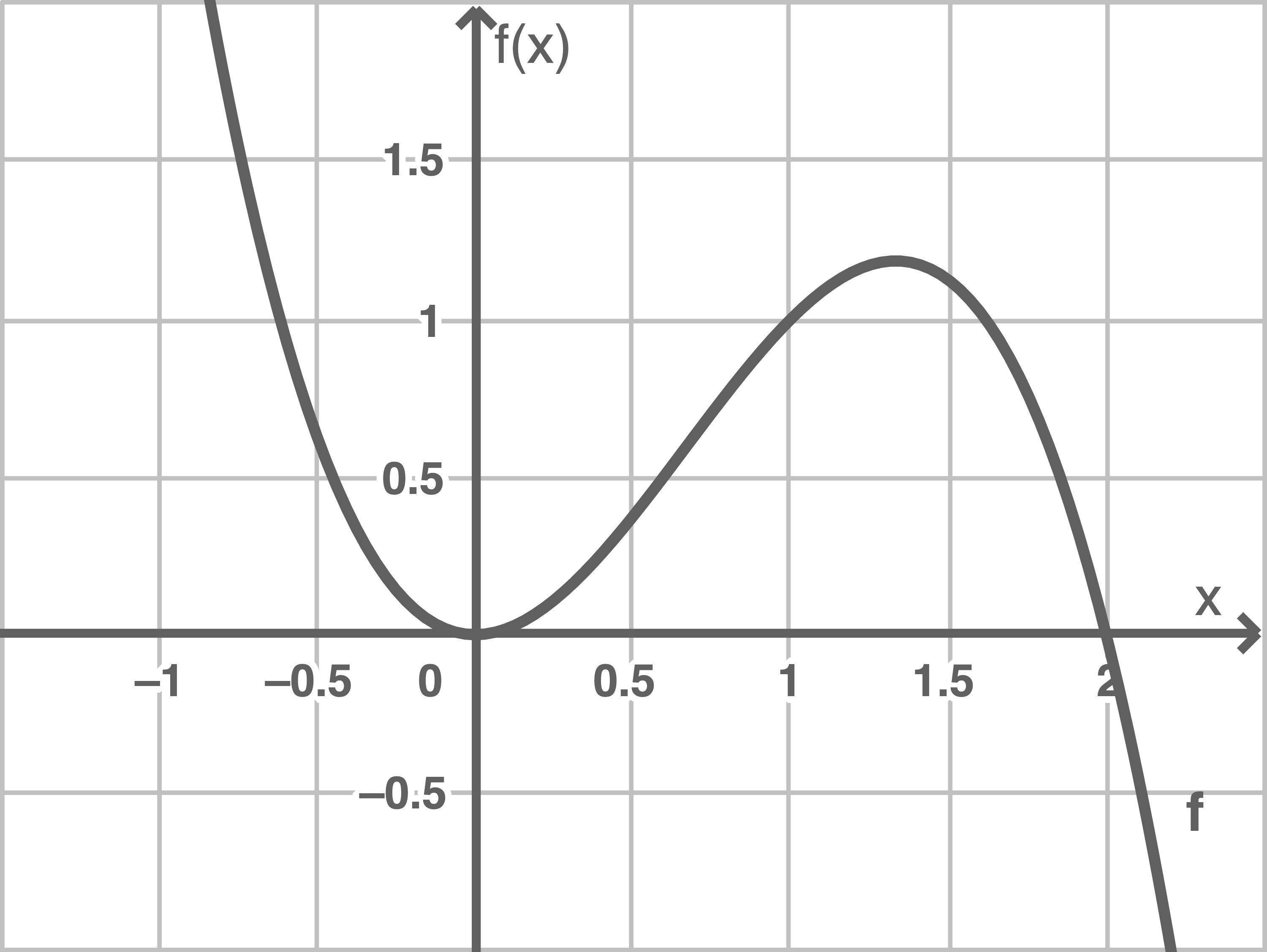
Abbildung
a)
Bestimme rechnerisch eine Gleichung der Tangente  an den Graphen von
an den Graphen von  im Punkt
im Punkt 
(4 Punkte)
b)
(1)
Gib die Koordinaten eines Punktes  an, in dem der Graph von
an, in dem der Graph von  die Steigung null hat.
die Steigung null hat.
(2)
Gib die Koordinaten eines Punktes  an, sodass die Ableitung von
an, sodass die Ableitung von  an der Stelle
an der Stelle  negativ ist.
negativ ist.
(1+1 Punkte)
Aufgabe 2: Stochastik
In einer Urne befinden sich schwarze (s) und weiße (w) Kugeln, die zusäzlich entweder mit dem Buchstaben A oder dem Buchstaben B beschriftet sind. Aus der Urne wird eine Kugel gezogen. Dieses Zufallsexperiment ist in dem folgenden unvollständig beschrifteten Baumdiagramm dargestellt.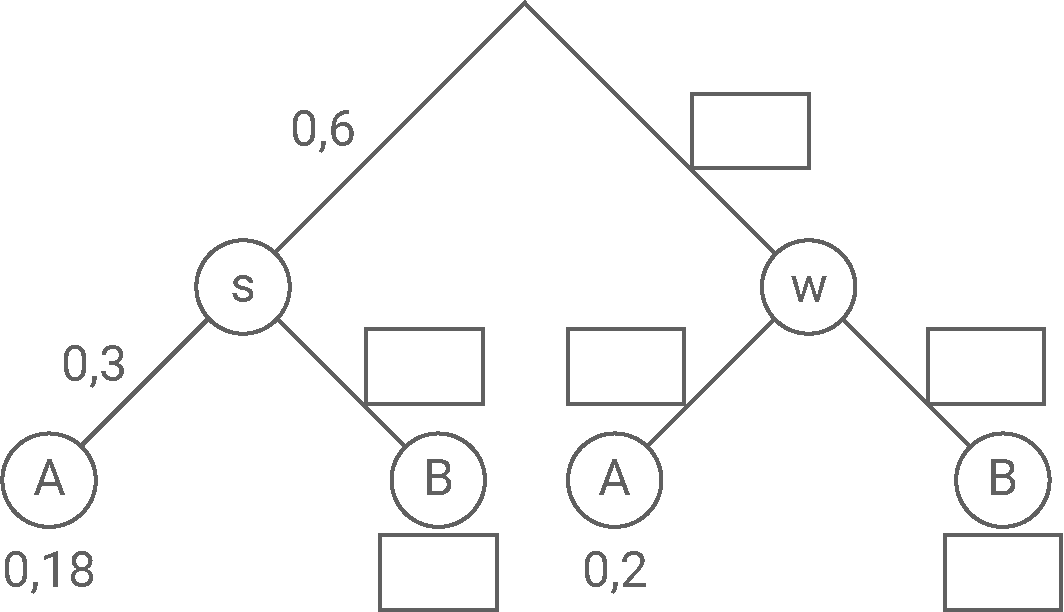
Baumdiagramm
a)
Ermittle die fehlenden Wahrscheinlichkeiten und gib diese in den Rechtecken im Baumdiagramm an.
(4 Punkte)
b)
Von der gezogenen Kugel wird zunächst nur bekannt gegeben, dass sie mit dem Buchstaben A beschriftet ist.
Stelle einen Term für die Wahrscheinlichkeit auf, dass es sich um eine schwarze Kugel handelt.
[Eine Berechnung der Wahrscheinlichkeit ist nicht erforderlich.]
(2 Punkte)
Lösung 1
a)
1. Schritt: Tangentengleichung aufstellen
Für die Gleichung einer Tangente  an dem Graphen von
an dem Graphen von  im Punkt
im Punkt  gilt:
gilt:
 2. Schritt: Steigung bestimmen
Für die Steigung wird die erste Ableitung einer Funktion bestimmt.
Für die erste Ableitungsfunktion der Funktion
2. Schritt: Steigung bestimmen
Für die Steigung wird die erste Ableitung einer Funktion bestimmt.
Für die erste Ableitungsfunktion der Funktion  folgt:
folgt:
![\(\begin{array}[t]{rll}
f(x)&=& -x^3+2 \cdot x^2\\[5pt]
f](https://www.schullv.de/resources/formulas/9b7e8518cb14eb3e16ac85726351934e0883e1c45456f350a0a2a9c94642003f_light.svg) Die Steigung
Die Steigung  beträgt im Punkt
beträgt im Punkt  also
also  Somit ergibt sich für die Tangentengleichung:
Somit ergibt sich für die Tangentengleichung:
![\(\begin{array}[t]{rll}
t(x)&=& f](https://www.schullv.de/resources/formulas/860a0b19e66f7a8385e7b8cef660d4d56b6e7f211a22ea599e19fb03ca79a1b8_light.svg) Damit lautet die Tangentengleichung
Damit lautet die Tangentengleichung 
b)
(1)
An dem Graphen der Funktion  lässt sich erkennen, dass an dem Punkt
lässt sich erkennen, dass an dem Punkt  die Steigung des Graphen von
die Steigung des Graphen von  ist.
Alternativ lassen sich die Punkte, an denen
ist.
Alternativ lassen sich die Punkte, an denen  die Steigung null hat, auch rechnerisch ermitteln. Dafür wird die erste Ableitung der Funktion gleich null gesetzt.
die Steigung null hat, auch rechnerisch ermitteln. Dafür wird die erste Ableitung der Funktion gleich null gesetzt.
![\(\begin{array}[t]{rll}
f](https://www.schullv.de/resources/formulas/442524e113c16ffc0f522ca8f970002e2a6a98169549907cb88122b3abe1da22_light.svg) Mit dem Satz vom Nullprodukt folgt
Mit dem Satz vom Nullprodukt folgt  Die zweite Lösung der Gleichung ergibt sich damit wie folgt:
Die zweite Lösung der Gleichung ergibt sich damit wie folgt:
![\(\begin{array}[t]{rll}
-3x+4&=& 0 \quad \scriptsize \mid\;+3x\\[5pt]
4&=& 3x \quad \scriptsize \mid\;:3\\[5pt]
\dfrac{4}{3}&=& x_2 \\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/fc6f1dae3692de7367ca0201543ce525a3ae1797ab9af229e2d6e1a59a77171b_light.svg) Somit ergeben sich die Stellen
Somit ergeben sich die Stellen  und
und  . Um die zugehörigen
. Um die zugehörigen  -Koordinaten zu erhalten, werden die beiden
-Koordinaten zu erhalten, werden die beiden  -Koordinaten in die Anfangsfunktion eingesetzt.
-Koordinaten in die Anfangsfunktion eingesetzt.
![\(\begin{array}[t]{rll}
f(0)&=& -0^3+2\cdot0^2 & \\[5pt]
&=& 0
\end{array}\)](https://www.schullv.de/resources/formulas/a45379921acf8eccbcc58a67454f17044823e8c9ed97704f884d1697224c842e_light.svg)
![\(\begin{array}[t]{rll}
f\left(\dfrac{4}{3}\right)&=& -\left(\dfrac{4}{3}\right)^3+2\cdot \left(\dfrac{4}{3}\right)^2 & \\[5pt]
&=& \dfrac{32}{27}
\end{array}\)](https://www.schullv.de/resources/formulas/882b7cb4940dd312515305ec23416fe43eb8514b9966cedcbed282d80e9aecba_light.svg) So ergeben sich die Punkte
So ergeben sich die Punkte  und
und 
(2)
Ist die Ableitung der Funktion  negativ, so hat der Graph von
negativ, so hat der Graph von  eine negative Steigung. An der Stelle
eine negative Steigung. An der Stelle  hat
hat  eine negative Steigung. So ergibt sich der Punkt
eine negative Steigung. So ergibt sich der Punkt 
Lösung 2
a)
Wahrscheinlichkeiten ermitteln:
Für die Wahrscheinlichkeiten folgen mit der Gegenwahrscheinlichkeit und den Pfadregeln:
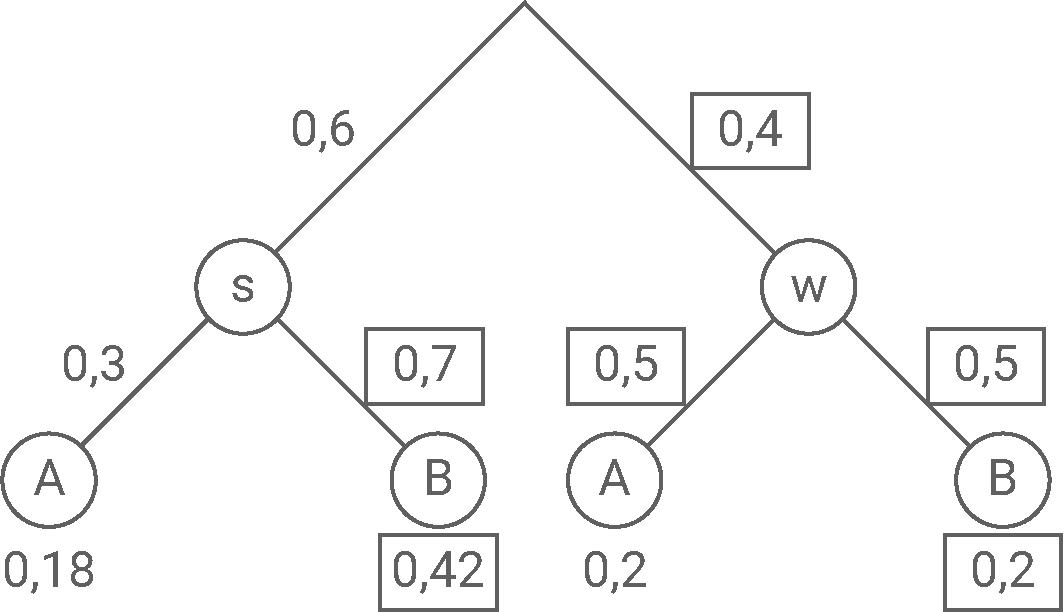

b)
Wahrscheinlichkeiten bestimmen:
Es ist die Wahrscheinlichkeit dafür gesucht, dass die Kugel schwarz ist und unter der Voraussetzung, dass sie mit dem Buchstaben  beschriftet ist. Somit ist die bedingte Wahrscheinlichkeit
beschriftet ist. Somit ist die bedingte Wahrscheinlichkeit  gesucht.
Mit der Formel für die bedingte Wahrscheinlichkeit folgt:
gesucht.
Mit der Formel für die bedingte Wahrscheinlichkeit folgt:
 Für die Wahrscheinlichkeit
Für die Wahrscheinlichkeit  folgt mit dem Satz für die totale Wahrscheinlichkeit:
folgt mit dem Satz für die totale Wahrscheinlichkeit:
 Somit ergibt sich für den Term der gesuchten Wahrscheinlichkeiten mit den zuvor bestimmten Wahrscheinlichkeiten:
Somit ergibt sich für den Term der gesuchten Wahrscheinlichkeiten mit den zuvor bestimmten Wahrscheinlichkeiten:
![\(\begin{array}[t]{rll}
P(s \mid A)&=&\dfrac{P(A \cap s)}{P(A \cap s)+P(A \cap w)}\\[5pt]
&=&\dfrac{0,18}{0,18+0,2}\\[5pt]
&=&\dfrac{0,18}{0,38}\\[5pt]
&=&\dfrac{9}{19}\\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/5565f13d0738c1818a6293eaa3d2c8bdb87940edaea081cb76d4fbeb672c50d2_light.svg) Damit lautet der Term für die gesuchte Wahrscheinlichkeit
Damit lautet der Term für die gesuchte Wahrscheinlichkeit 