Prüfungsteil A: Ohne Hilfsmittel
Aufgabe 1: Analysis
Gegeben ist die Funktion  mit der Gleichung
mit der Gleichung  Untersuche die Funktion
Untersuche die Funktion  rechnerisch auf lokale Minimal- und Maximalstellen.
rechnerisch auf lokale Minimal- und Maximalstellen.
(6 Punkte)
Aufgabe 2: Stochastik
Beim Spiel „Die wilde 8“ wird das Glücksrad mit den beiden Zahlen 0 und 8 (siehe Abbildung) zweimal gedreht.
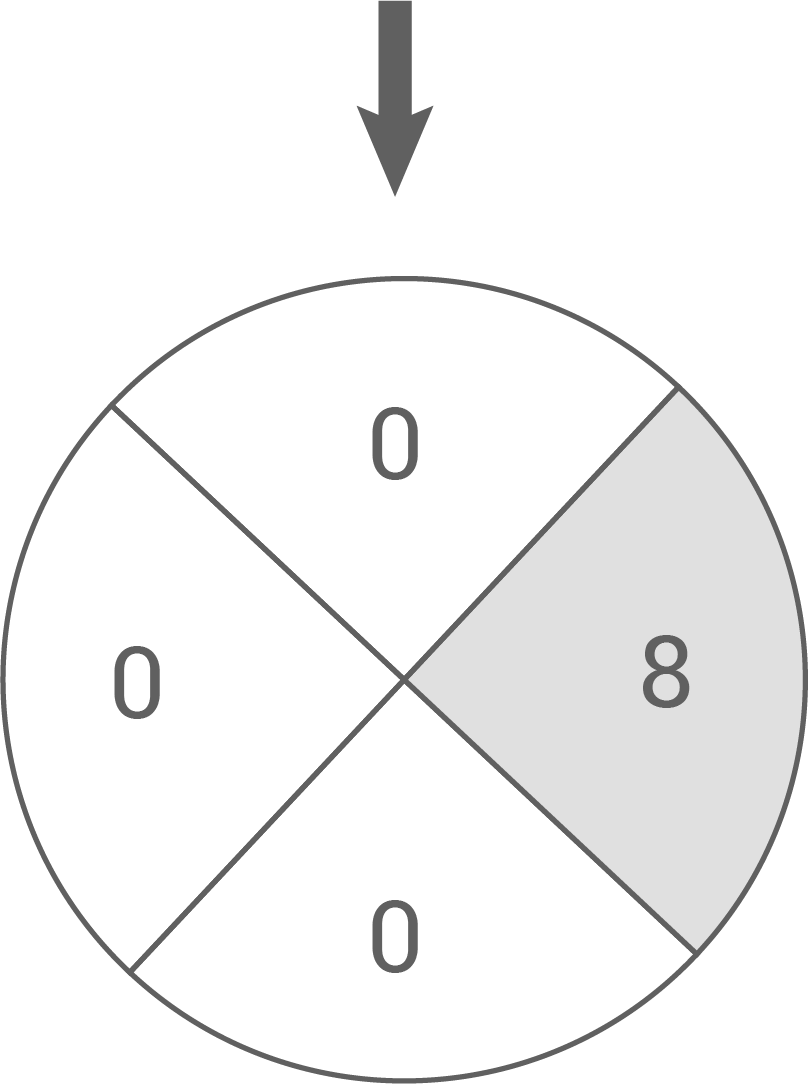

Abbildung
a)
Erstelle für dieses Zufallsexperiment ein vollständig beschriftetes Baumdiagramm mit allen Pfadwahrscheinlichkeiten.
(2 Punkte)
b)
Die beiden Zahlen in den Feldern, auf die jeweils der Pfeil zeigt, werden addiert.
(1)
Berechne die Wahrscheinlichkeiten dafür, dass sich
- die Summe 0 ergibt,
- die Summe 8 ergibt,
- die Summe 16 ergibt.
(2)
Der Spieleinsatz für das zweimalige Drehen des Glücksrades beim Spiel „Die wilde 8“ beträgt 8 €.
- Bei der Summe 0 gibt es keine Auszahlung, der Spieleinsatz ist verloren.
- Bei der Summe 8 wird der Spieleinsatz zurückgezahlt.
- Bei der Summe 16 wird der zehnfache Spieleinsatz ausgezahlt.
(2+2 Punkte)
Lösung 1
1. Schritt:  ableiten
ableiten
![\(\begin{array}[t]{rll}
f](https://www.schullv.de/resources/formulas/c8f56006acd319828af4feb5cc63821ccea8fe93a09f53b678298fc4e9e62b12_light.svg) 2. Schritt: Notwendiges Kriterium anwenden
3. Schritt: Vorzeichenwechselkriterium anwenden
2. Schritt: Notwendiges Kriterium anwenden
3. Schritt: Vorzeichenwechselkriterium anwenden
![\(\begin{array}[t]{rll}
f](https://www.schullv.de/resources/formulas/7732288b4e0895310399217f643f987f3ca5f1910eef1257a40b5d2a10d7bd87_light.svg)
![\(\begin{array}[t]{rll}
f](https://www.schullv.de/resources/formulas/efc54a25a4368edb90d884142e98d55833c846581b76e3277e0729393a6c147a_light.svg)
![\(\begin{array}[t]{rll}
f](https://www.schullv.de/resources/formulas/a2195dff1830bfb0f8120a6e4332afcd50a274f730c567eb1c6b99624fb78a3c_light.svg) An der Stelle
An der Stelle  liegt ein Vorzeichenwechsel von + zu - vor. Es handelt sich also um eine Maximumstelle.
An der Stelle
liegt ein Vorzeichenwechsel von + zu - vor. Es handelt sich also um eine Maximumstelle.
An der Stelle  liegt ein Vorzeichenwechsel von - zu + vor. Es handelt sich also um eine Minimalstelle
liegt ein Vorzeichenwechsel von - zu + vor. Es handelt sich also um eine Minimalstelle
Lösung 2
a)
Jeder Kreissektor hat die Wahrscheinlichkeit  folglich gilt
folglich gilt  und
und 
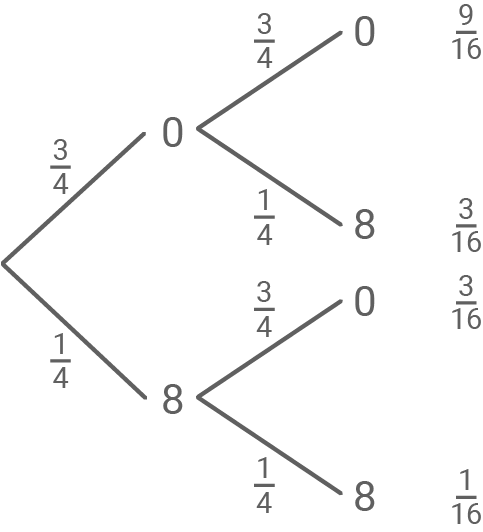

b)
(1)
(2)
Die Zufallsvariable  gibt den Gewinn an.
gibt den Gewinn an.
Werte in die Formel des Erwartungswerts einsetzen:
Da der Erwartungswert gleich  ist, ist das Spiel „Die wilde 8“ ein faires Spiel.
ist, ist das Spiel „Die wilde 8“ ein faires Spiel.
| Summe 0 | ||
|---|---|---|
| Summe 8 | ||
| Summe 16 |