Prüfungsteil A: Ohne Hilfsmittel

Aufgabe 1

Gegeben ist die Funktion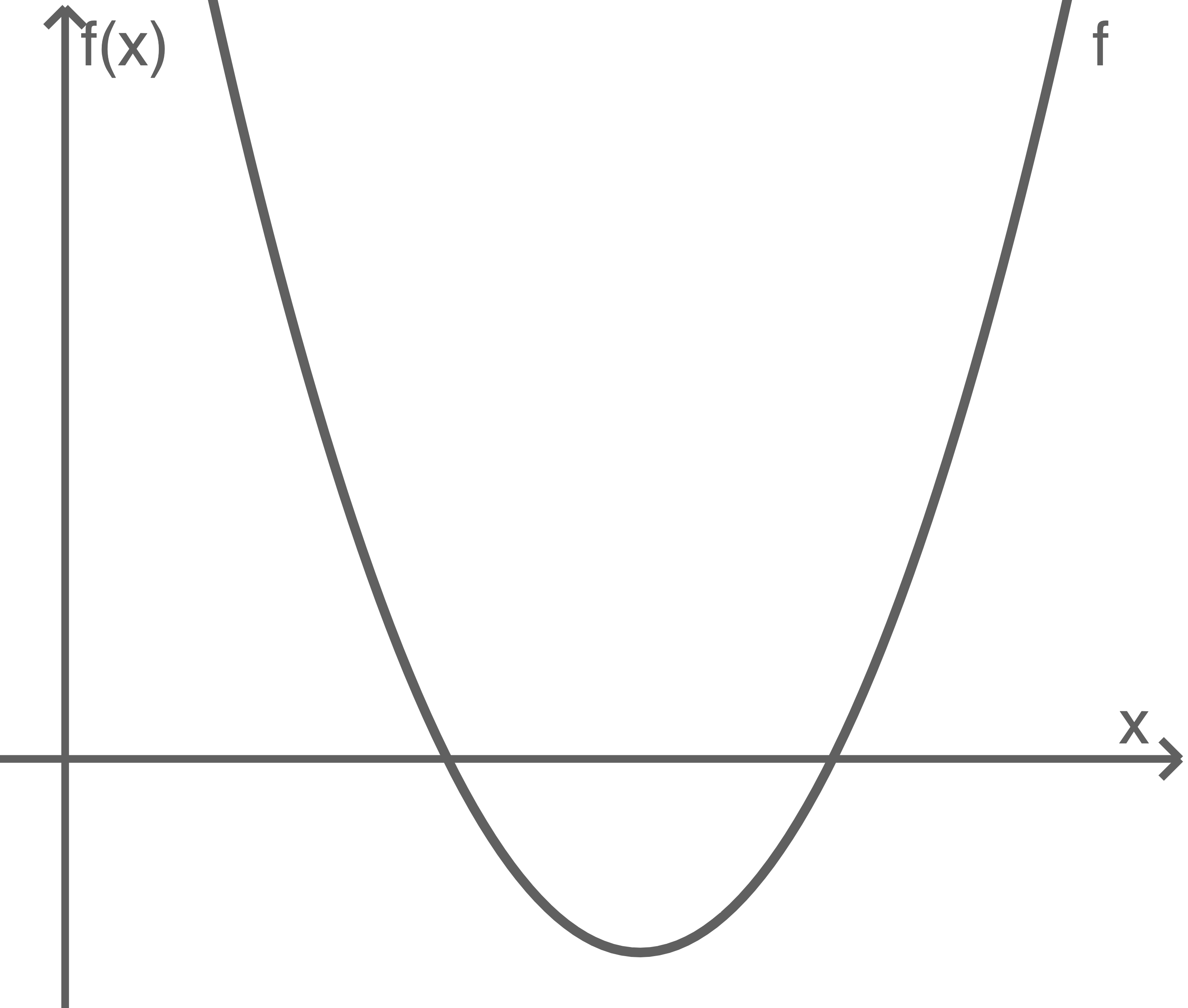 $f$ mit $f(x)=x^2- 6\cdot x+8, x\in \mathbb{R}.$

Die Abbildung 1 zeigt den Graphen von $f.$

Hilfsmittelfreier Teil koordinatensystem graph

Abbildung 1

Berechne die Nullstellen der Funktion $f.$

(3 Punkte)

(1)

Berechne $\(f$

(2)

Eine der drei Abbildungen 2.1 bis 2.3 zeigt den Graphen von $\(f$

Abbildung 2.1

Abbildung 2.2

Abbildung 2.3

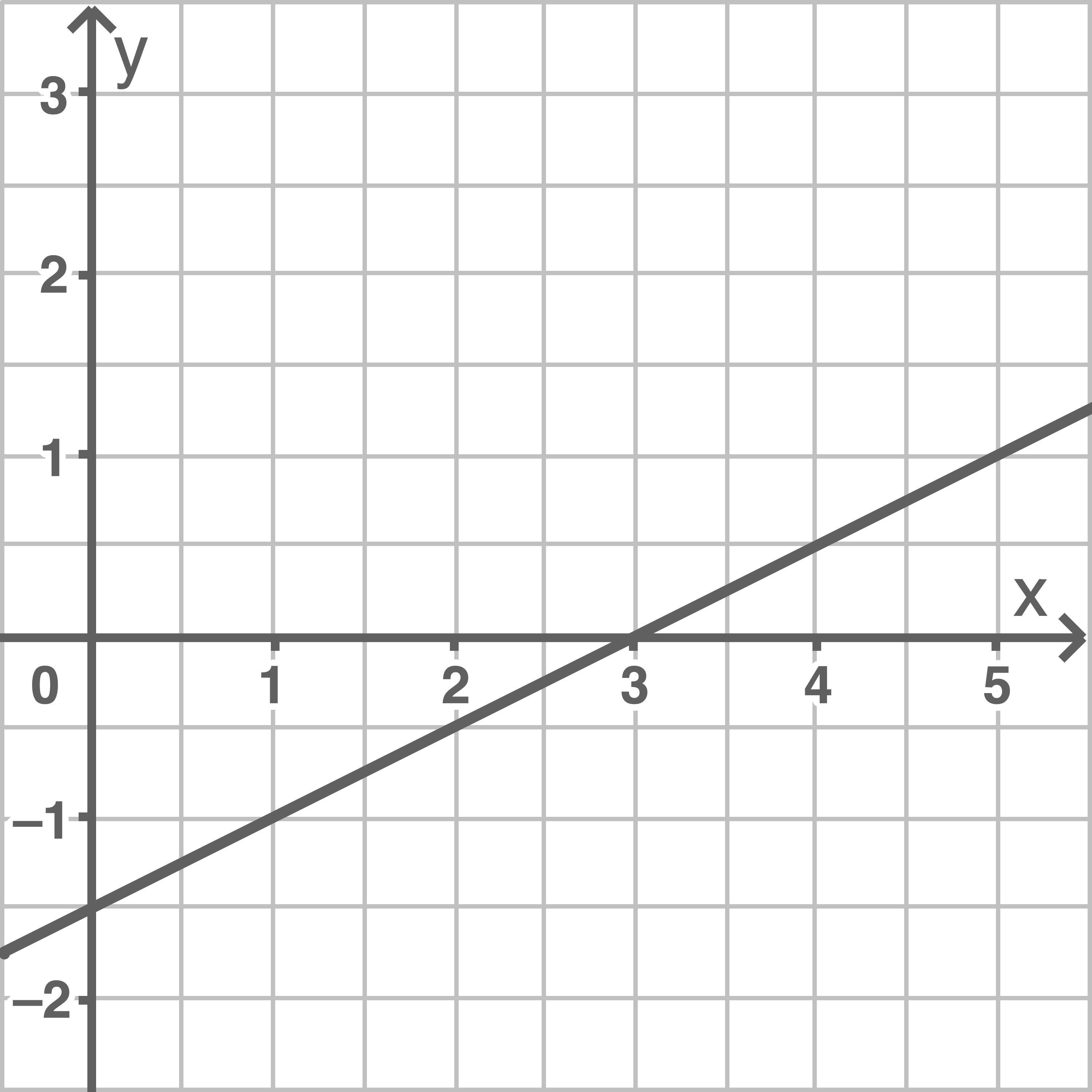
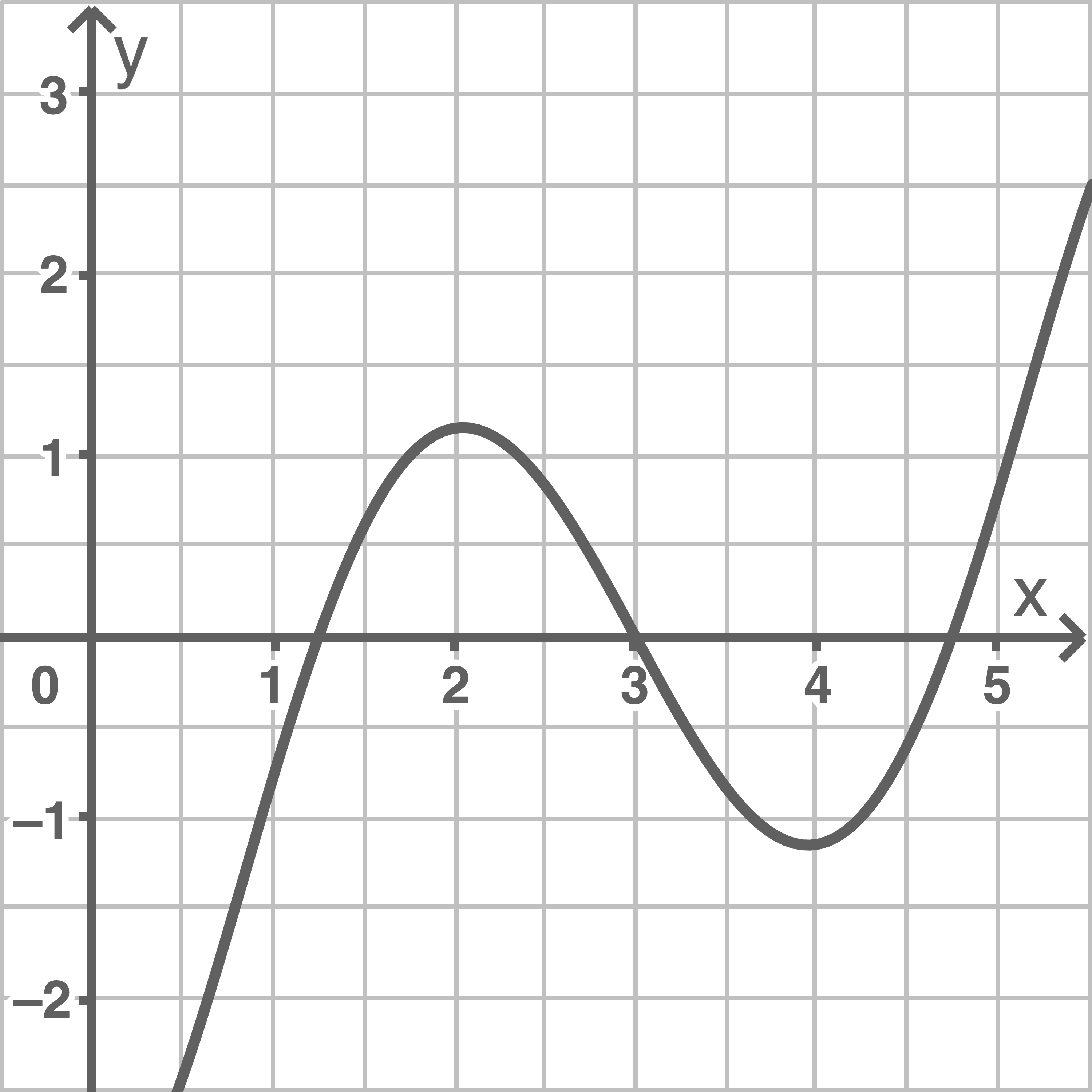
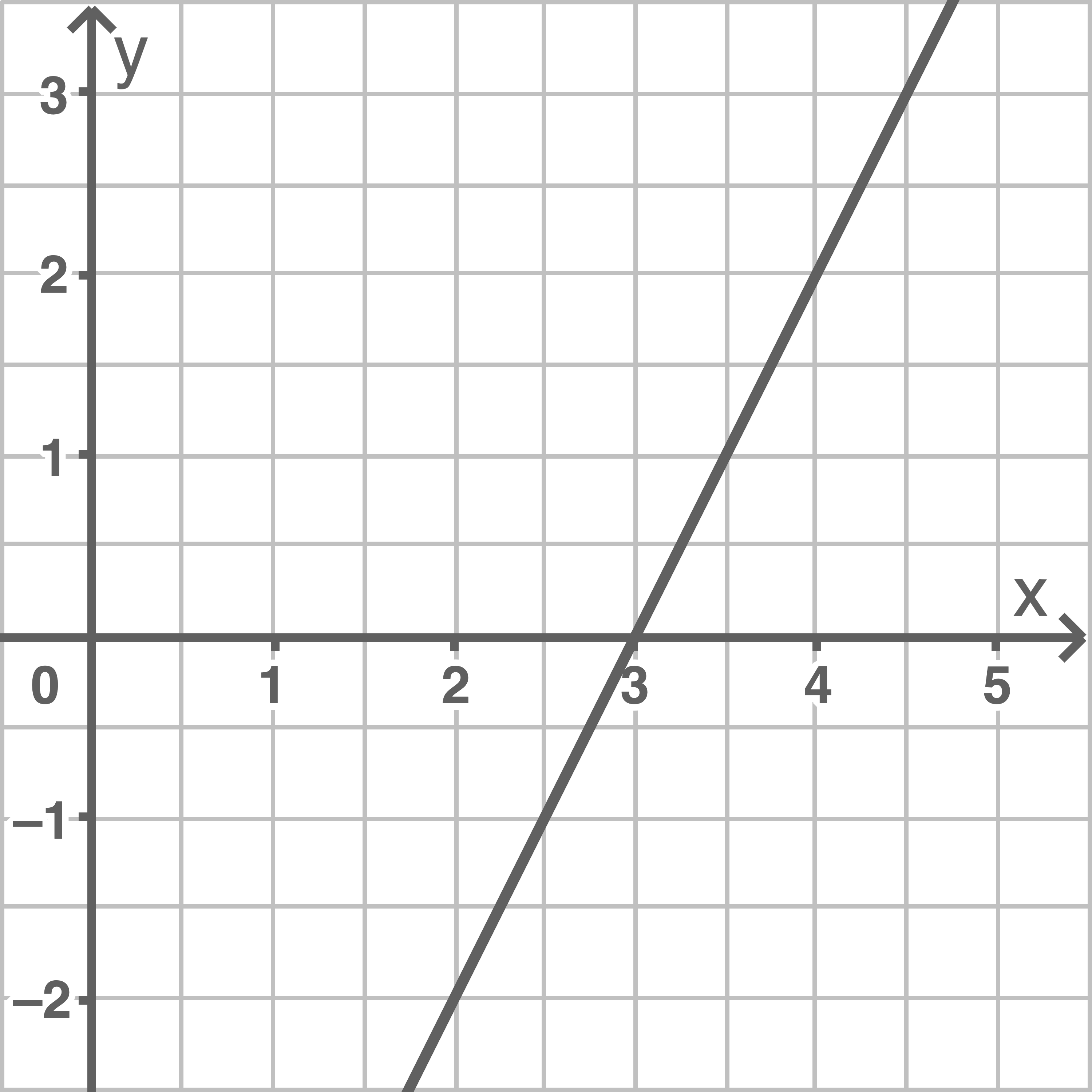Gib an, welche Abbildung den Graphen von $\(f$ zeigt.

(2 + 1 Punkte)

Aufgabe 2

Teuer oder billig, kann man das schmecken?

Die 32 Kinder einer Klasse führen einen Schokoladentest durch. Acht Kinder erhalten teure Schokolade und die übrigen billige Schokolade. Nur die Lehrkraft weiß, zu welcher der beiden Preisklassen die Schokolade jeweils gehört.

Nach dem Verzehr äußert jedes Kind eine Vermutung darüber, zu welcher Preisklasse seine Schokolade gehört.

In der folgenden Tabelle sind bereits einige der Werte eingetragen, die sich bei diesem Test ergeben haben.

	Kind hat teure Schokolade erhalten.	Kind hat billige Schokolade erhalten.	Summe
Kind vermutet: Die Schokolade ist teuer.			12
Kind vermutet: Die Schokolade ist billig.	6	14	20
Summe			32

(1)

Gib die fehlenden Werte in der Tabelle an.

(2)

Ein Kind wird zufällig ausgewählt.

Berechne die Wahrscheinlichkeit, dass dieses Kind die Preisklasse seiner Schokolade richtig vermutet.

(3)

Ein zufällig ausgewähltes Kind vermutet, es habe eine billige Schokolade erhalten.

Bestimme die Wahrscheinlichkeit, dass das Kind tatsächlich aber eine teure Schokolade erhalten hat.

(2 + 2 + 2 Punkte)

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?

Lösung 1

$f(x)=0$ setzen:

$\begin{array}[t]{rll} x^2- 6\cdot x+8 &=& 0\quad \scriptsize \mid\; \,\text{p,q-Formel} \\[5pt] x_{1,2}&=& \dfrac{6}{2}\pm \sqrt{\left(\dfrac{-6}{2}\right)^2- 8} &\quad \scriptsize \\[5pt] x_{1,2}&=& 3\pm \sqrt{(-3)^2- 8} &\quad \scriptsize \\[5pt] x_{1,2}&=& 3\pm \sqrt{9- 8} &\quad \scriptsize \\[5pt] x_{1,2}&=& 3\pm 1 &\quad \scriptsize \\[5pt] x_1&=& 2 &\quad \scriptsize \\[5pt] x_2&=& 4 \end{array}$

(1)

1. Schritt: $\(\boldsymbol{f$ bestimmen

$\(f$

2. Schritt: $\(\boldsymbol{f$ berechnen

$\(\begin{array}[t]{rll} f$

(2)

Der Graph von $\(f$ gehört zur Abbildung 2.3, da $\(f$ eine lineare Funktion mit der Steigung 2 ist.

Lösung 2

(1)

Die ersten Werte können aus dem Text übernommen werden, die restlichen Werte müssen berechnet werden.

	Kind hat teure Schokolade erhalten.	Kind hat billige Schokolade erhalten.	Summe
Kind vermutet: Die Schokolade ist teuer.	2	10	12
Kind vermutet: Die Schokolade ist billig.	6	14	20
Summe	8	24	32

(2)

$\begin{array}[t]{rll} P(\text{Preis richtig vermutet})&=& \dfrac{2}{32}+\dfrac{14}{32} &\quad \scriptsize \\[5pt] &=& \dfrac{16}{32} = \dfrac{1}{2} \end{array}$

(3)

$\begin{array}[t]{rll} P (\text{Die Schokolade ist teuer.}\,|\,\text{Vermutung: Die Schokolade ist billig.})&=& \dfrac{6}{20} = \dfrac{3}{10} &\quad \scriptsize \\[5pt] \end{array}$

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?