Prüfungsteil B: Mit Hilfsmitteln

Aufgabe 3

Gegeben ist die Funktion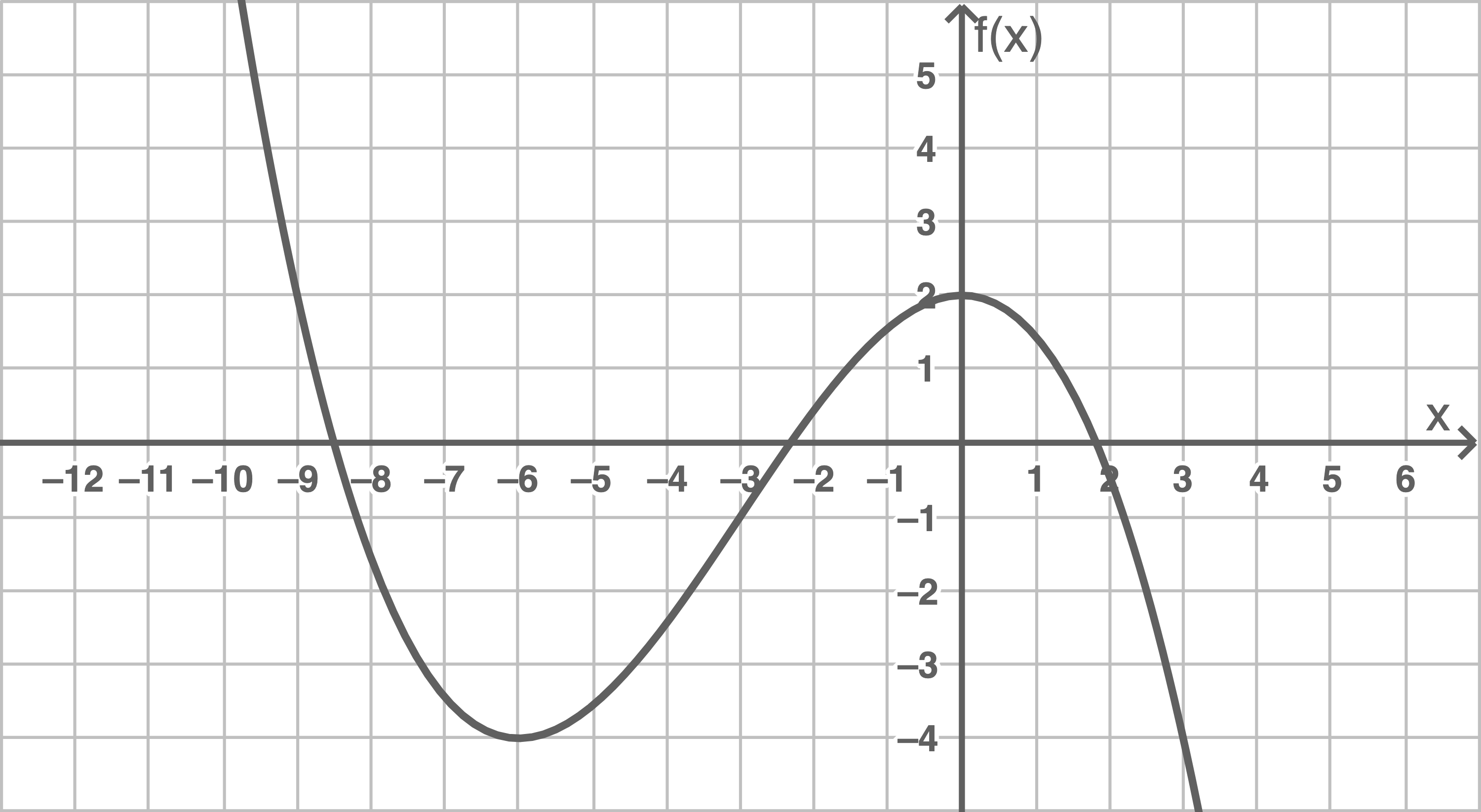 $f$ mit

$f(x) = -\dfrac{1}{18} \cdot x^3 - \dfrac{1}{2} \cdot x^2 + 2, \, x \in \mathbb{R}.$

Die Abbildung zeigt den Graphen der Funktion $f$ .

nrw zk zum ende der ef 2024, zentrale klausur

Abbildung

Gib, z.B. anhand des Graphen von $f,$ den Bereich an, in dem $\(f$ gilt.

(2 Punkte)

Untersuche rechnerisch die Funktion $f$ auf Wendestellen.

(4 Punkte)

(1)

(i)

Berechne eine Gleichung der Normale $n$ des Graphen von $f$ im Punkt $W(-3|f(-3)).$

[Zur Kontrolle: $n: y = -\dfrac{2}{3} \cdot x - 3$ .]

(ii)

Zeichne die Normale $n$ in die Abbildung ein.

(2)

Zeichne die Tangente $t: y = \dfrac{3}{2} \cdot x + \dfrac{7}{2}$ an den Graphen von $f$ im Punkt $W$ ebenfalls in die Abbildung ein.

(3)

Die Normale $n$ , die Tangente $t$ und die $y$ -Achse schließen ein Dreieck ein.

Berechne den Flächeninhalt des Dreiecks.

(5 + 1 + 3 Punkte)

Ausgehend von der Funktion $f$ wird nun die Gleichung einer transformierten Funktion $f_\text{neu}$ gesucht.

Der Graph von $f$ besitzt den lokalen Tiefpunkt $T(-6 \mid-4)$ .

Der Graph der Funktion $f_\text{neu}$ entsteht durch Verschiebungen aus dem Graphen der Funktion $f$ . Der lokale Tiefpunkt $T$ wird dabei in den Ursprung des Koordinatensystems verschoben.

Gib eine Gleichung von $f_\text{neu}$ an.

(2 Punkte)

Für jede Zahl $a \in \mathbb{R},$ $a \neq 0,$ ist durch die Gleichung $f_a(x)=f(a \cdot x)$ eine Funktion $f_a$ definiert.

(1)

Beschreibe, wie der Graph von $f_2$ aus dem Graphen von $f$ entsteht.

(2)

Bestimme alle Werte von $a \in \mathbb{R},$ $a \neq 0,$ für die $x=1$ eine Nullstelle von $f_a$ ist.

(2 + 2 Punkte)

Die Funktion $f$ ist die Ableitungsfunktion einer Funktion $F$ .

Gib an, wie viele lokale Minimal- und wie viele lokale Maximalstellen die Funktion $F$ besitzt, und begründe deine Angaben.

(3 Punkte)

Aufgabe 4

Abbildung 1: Holzpellets^[1]

Als Alternative zu Gas und Öl können auch Holzpellets als Brennstoff für Heizungen genutzt werden. Holzpellets werden aus Abfallprodukten der Holzindustrie hergestellt. Im Gegensatz zu Gas und Öl handelt es sich hierbei um einen nachwachsenden Rohstoff.

Der jeweilige Preis (in €) für eine Tonne Holzpellets von Anfang Januar 2022 bis Anfang Dezember 2022 kann für $0 \leq t \leq 11$ näherungsweise mithilfe der auf $\mathbb{R}$ definierten Funktion $f$ mit

$f(t) = -2{,}5 \cdot t^3 + 39{,}375 \cdot t^2 - 101{,}25 \cdot t + 370$

beschrieben werden, wobei $t$ die Zeit in Monaten angibt.

$t = 0$ entspricht dem 01.01.2022,
$t = 1$ entspricht dem 01.02.2022,
$t = 2$ entspricht dem 01.03.2022 usw.

(1)

Berechne den Preis für eine Tonne Holzpellets am 01.03.2022 und am 01.05.2022.

(2)

Berechne, um wie viel Prozent der Preis in diesem Zeitraum gestiegen ist.

(2 + 2 Punkte)

Berechne die Länge des Zeitraums, in dem eine Tonne Holzpellets mindestens $800 \,\text{€}$ gekostet hat.

(4 Punkte)

Untersuche rechnerisch, zu welchem Zeitpunkt jeweils der niedrigste und der höchste Preis für die Holzpellets im Modellierungszeitraum vorgelegen hat, und gib den Unterschied zwischen diesen Preisen an.

(6 Punkte)

Die Sekante, die durch den lokalen Tiefpunkt und den lokalen Hochpunkt des Graphen der Funktion $f$ verläuft, wird mit $s$ bezeichnet.

Berechne die Steigung der Sekante $s$ und interpretiere diese Steigung im Sachzusammenhang.

(4 Punkte)

(1)

Berechne $\(f(11)+f$

(2)

Interpretiere den in e) (1) berechneten Wert im Sachzusammenhang.

(1 + 2 Punkte)

Eine Familie wird zu einem Zeitpunkt $t$ im Jahr 2022 mit $3500 \,\text{kg}$ Pellets beliefert. Neben den Kosten für Holzpellets fallen dafür auch Lieferkosten in Höhe von 90 € an.

Gib eine Gleichung der Funktion $p$ an, durch die der Gesamtpreis $p(t)$ (in €) für diese Lieferung in Abhängigkeit vom Zeitpunkt $t$ gegeben ist.

(3 Punkte)

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?

Lösung 3

Der Graph von $f$ steigt im Bereich $[-6;0],$ dort gilt daher $\(f$

$f(x)=-\dfrac{1}{18} \cdot x^3-\dfrac{1}{2} \cdot x^2+2$

$\(f$

Notwendiges Kriterium für Wendestellen anwenden:

$\(\begin{array}[t]{rll} f$

Hinreichendes Kriterium für Wendestellen überprüfen:

$\(f$

Die Funktion $f$ hat an der Stelle $x=-3$ eine Wendestelle.

(1)

(i)

$f(-3)=-\dfrac{1}{18} \cdot(-3)^3-\dfrac{1}{2} \cdot(-3)^2+2$ $=-1$

Die Normale verläuft also durch den Punkt $W(-3\mid -1).$

Für die Steigung der Funktion $f$ an dieser Stelle gilt:

$\(f$

Für die Steigung der Normalen an dieser Stelle folgt:

$m=-\dfrac{1}{\frac{3}{2}}=-\dfrac{2}{3}$

Die Normalengleichung ist also von der Form $n:y=-\dfrac{2}{3}x+c.$ Einsetzen der Koordinaten von $W$ liefert:

$\begin{array}[t]{rll} -1&=& -\dfrac{2}{3}\cdot (-3)+c \\[5pt] -1&=& 2+c \quad \scriptsize \mid\;-2 \\[5pt] -3&=& c \end{array}$

Damit ergibt sich die Gleichung der Normale zu:

$n:y=-\dfrac{2}{3}x-3$

(ii)

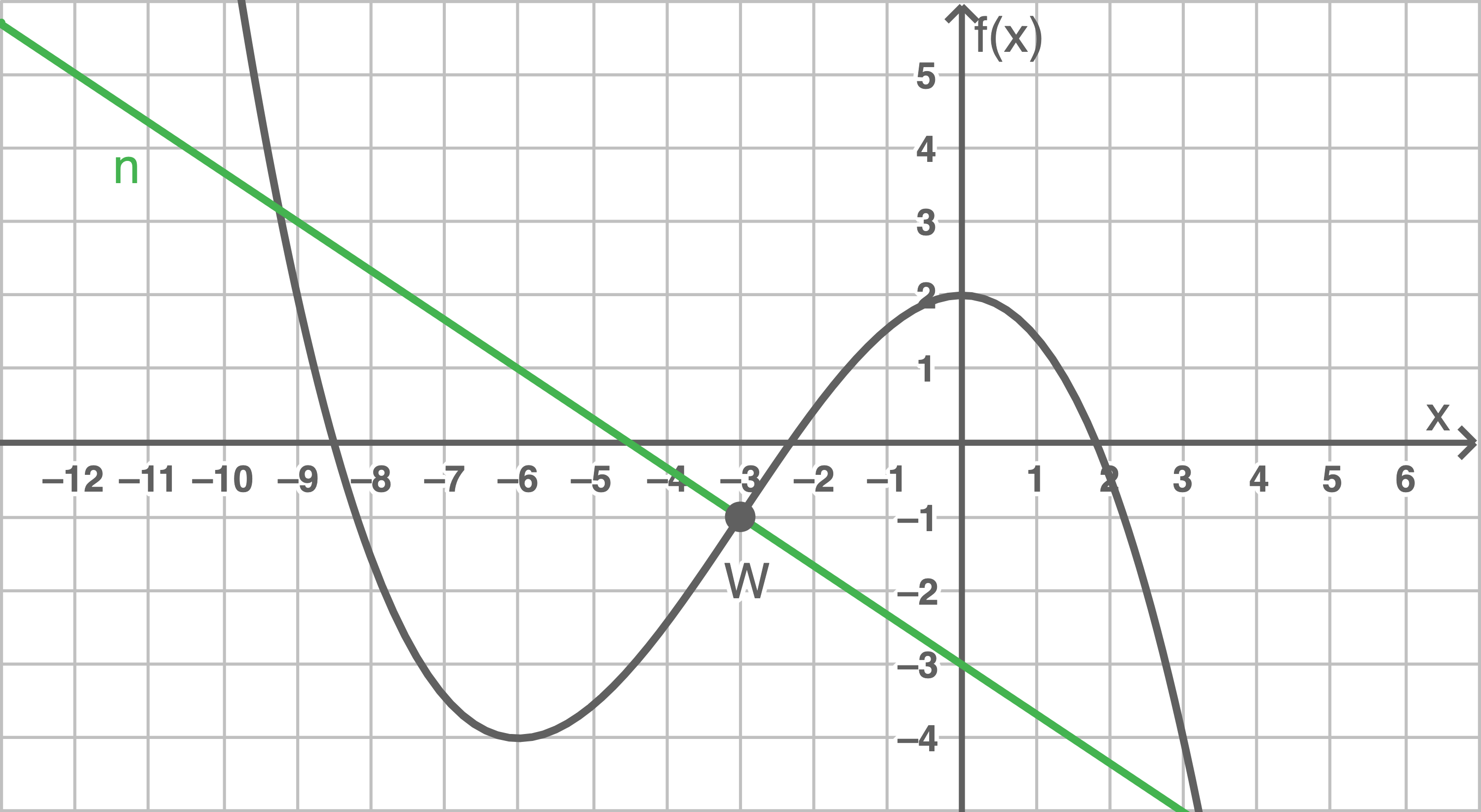
(2)

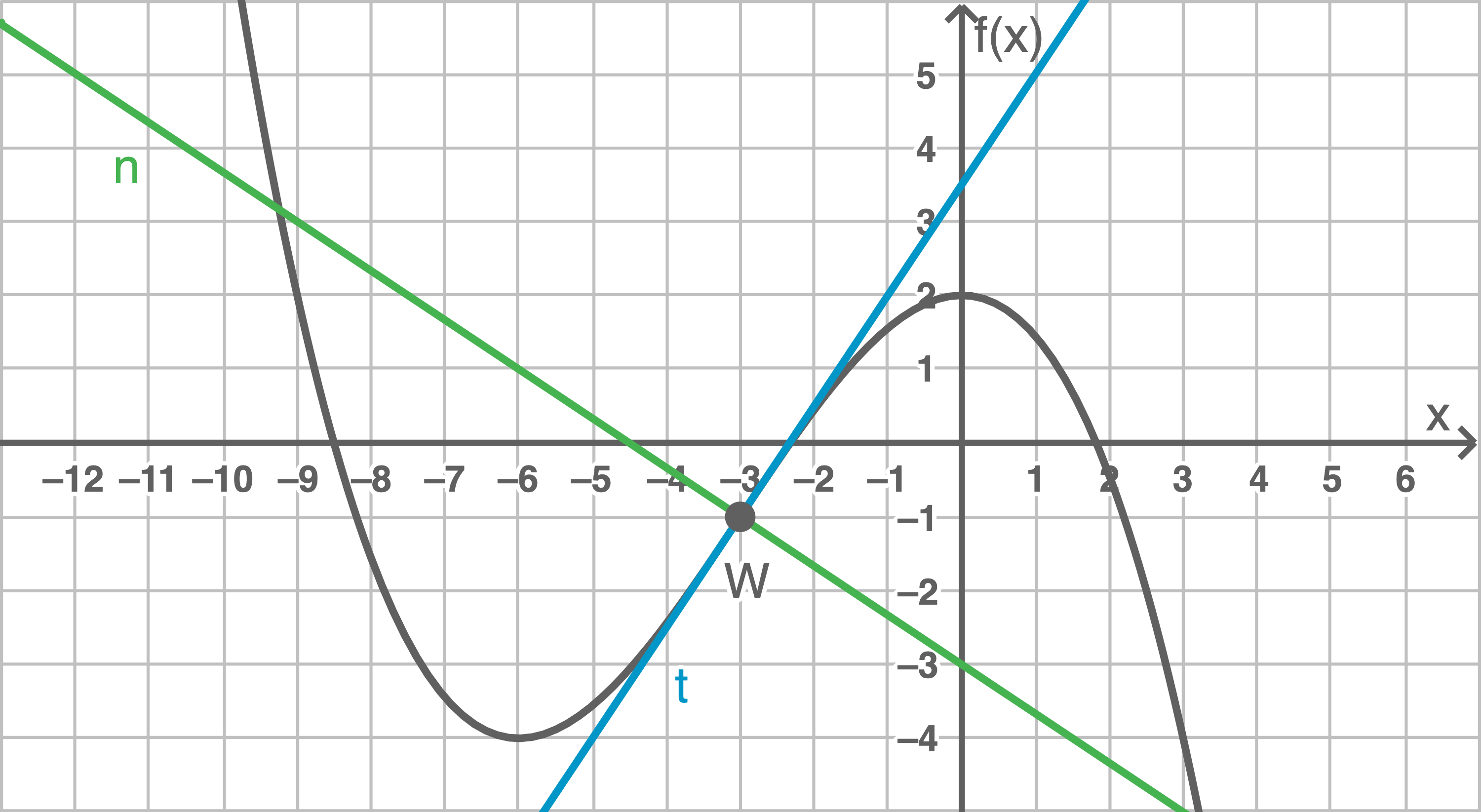
(3)

Die Tangente schneidet die $y$ -Achse bei:

$\dfrac{3}{2}\cdot 0+\dfrac{7}{2}=\dfrac{7}{2}$

Die Normale schneidet die $y$ -Achse bei:

$-\dfrac{3}{2}\cdot 0-3=-3$

Die Grundseite des Dreiecks halt also die Länge $g=\dfrac{7}{2}-(-3)=\dfrac{13}{2}$

Durch die Koordinaten des Punktes $W$ folgt außerdem die Höhe $h=3.$

Mit der Formel für den Flächeninhalt eines Dreiecks folgt:

$\begin{array}[t]{rll} A&=& \dfrac{1}{2}\cdot g\cdot h \\[5pt] &=& \dfrac{1}{2}\cdot \dfrac{13}{2}\cdot 3 \\[5pt] &=& \dfrac{39}{4} \,\text{[FE]} \end{array}$

Der Graph von $f$ muss um 6 Einheiten nach rechts und um 4 Einheiten nach oben verschoben werden:

Funktionsgleichung anzeigen

$f_\text{neu}(x)= f(x-6)+4$

(1)

Der Graph von $f_2$ entsteht aus dem Graphen von $f$ durch eine Streckung mit dem Faktor $\dfrac{1}{2}$ entlang der $x$ -Achse.

(2)

$f_a(1)=f(a\cdot 1)=f(a)$

Gesucht ist also die Lösung der folgenden Gleichung:

$\begin{array}[t]{rll} f(a)&=& 0 \\[5pt] -\dfrac{1}{18} \cdot a^3-\dfrac{1}{2} \cdot a^2+2&=& 0 \end{array}$

Mit dem MMS ergeben sich die Lösungen $a_1=-8,5,$ $a_2\approx-2,32$ und $a_3\approx 1,82.$

Nullstellen mit Vorzeichenwechsel von - nach + der Funktion $f$ sind lokale Minimalstellen der Funktion $F.$ Der Abbildung kann entnommen werden, dass $F$ daher eine lokale Minimalstelle hat.

Nullstellen mit Vorzeichenwechsel von + nach - der Funktion $f$ sind lokale Maximalstellen der Funktion $F.$ Der Abbildung kann entnommen werden, dass $F$ daher zwei lokale Maximalstellen hat.

Lösung 4

(1)

$f(2)=305$

$f(4)=435$

Am 01.03.2022 kostet eine Tonne Holzpellets 305 €, am 01.05.2022 kostet sie 435 €.

(2)

$:305$

$\cdot 435$ Grau geschwungener Pfeil, der nach rechts unten zeigt.

$\begin{array}{rcl} 305\,\text{€} & \mathrel{\widehat{=}}& 100\,\%\\[5pt] 1\,\text{€} & \mathrel{\widehat{=}}& \dfrac{100}{305}\,\%\\[5pt] 435\,\text{€} & \mathrel{\widehat{\approx}}& 143\,\% \end{array}$

$:305$

$\cdot 435$

Der Preis ist in diesem Zeitraum um $143\,\%-100\,\%=43\,\%$ gestiegen.

Die Gleichung $f(t)=800$ hat im betrachteten Zeitraum die Lösungen $t=8$ und $t\approx 9,9.$

Wegen $f(9)\approx 825,6$ ist der Preis für eine Tonne Holzpellets zwischen $t=8$ und $t\approx 9,9$ höher als $800\,\text{€}.$

Eine Tonne Holzpellets hat von Anfang September 2022 bis Ende Oktober 2022, also knapp 2 Monate lang, mindestens $800 \,\text €$ gekostet.

$\(f$

Notwendige Bedingung für Extremstellen anwenden:

$\(\begin{array}[t]{rll} f$

Mit dem MMS folgt $t_1=1,5$ und $t_2=9.$ An diesen Stellen und an den Randwerten liegen daher der potentiell niedrigste und höchste Preis für die Holzpellets im betrachteten Zeitraum.

$\begin{array}[t]{rll} f(0)&=& 370\\[5pt] f(1,5)&\approx& 298,28\\[5pt] f(9)&\approx& 825,63 \\[5pt] f(11)&=& 693,13 \end{array}$

Mitte Februar 2022 hat der niedrigste Preis für eine Tonne Holzpellets vorgelegen, Anfang Oktober 2022 war der Preis am höchsten.

Der Unterschied zwischen den Preisen beträgt $825,63-298,28=527,35\,\text{€}.$

Rechenweg anzeigen

$m \approx 70,31$

Während der Preissteigerung vom niedrigsten auf den höchsten Preis des Jahres 2022 stieg der Preis für eine Tonne Holzpellets durchschnittlich um ungefähr $70 \,\text€$ pro Monat.

(1)

$\(f(11)+f$

(2)

Wenn der Preis für Holzpellets am Ende des Modellierungszeitraums konstant weiter mit der zu diesem Zeitpunkt vorliegenden momentanen Änderungsrate gefallen wäre, hätte sich für Mitte Dezember 2022 ein Preis von ungefähr $622 \,\text €$ für eine Tonne Holzpellets ergeben.

$3500 \,\text{kg}=3,5\,\text{t}$

Damit folgt:

$p(t)=3,5\cdot f(t)+90$

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?