Prüfungsteil B: Mit Hilfsmitteln
Aufgabe 3
Gegeben ist die Funktion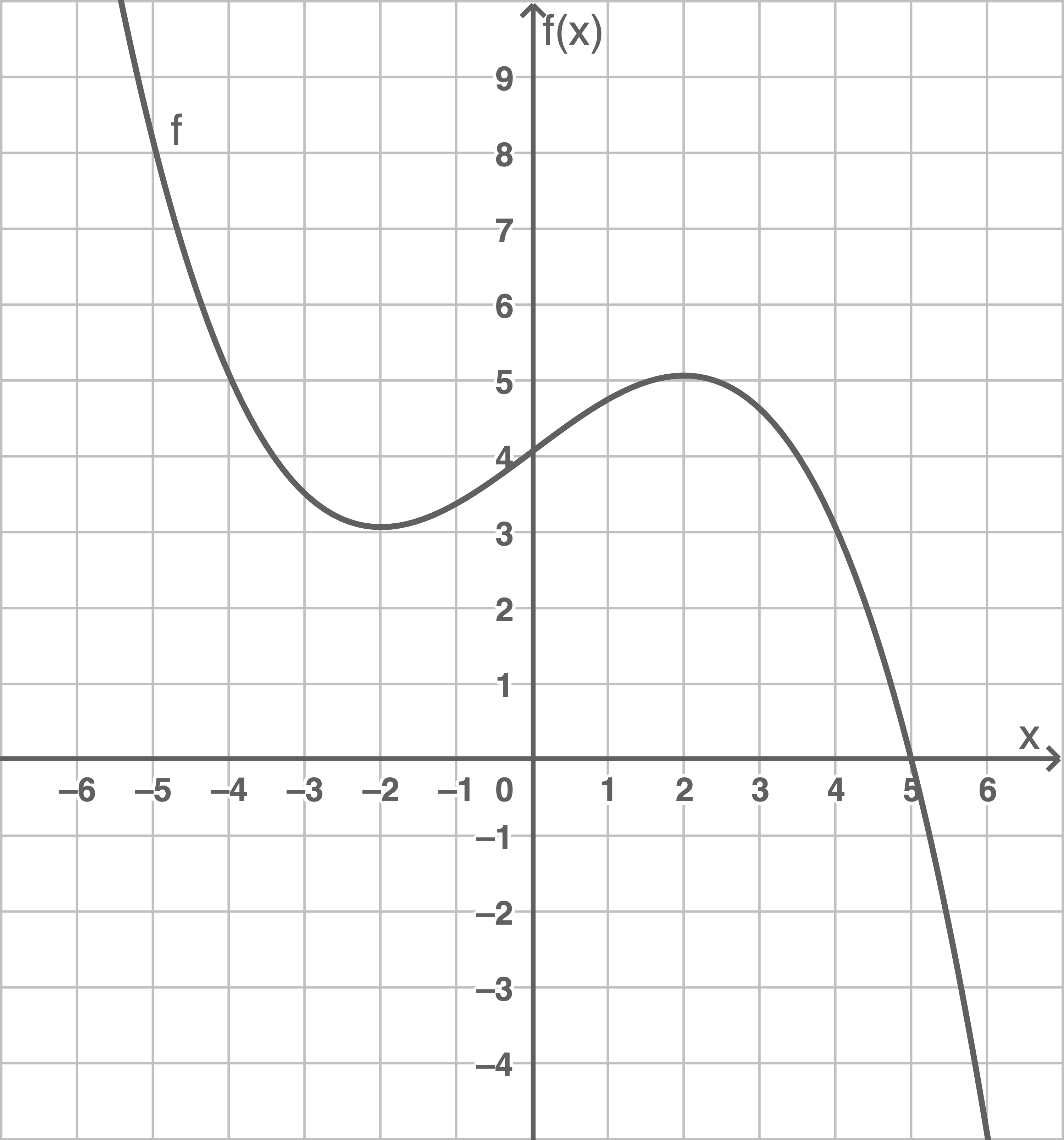
Abbildung
a)
Gib die exakten Koordinaten des Schnittpunktes des Graphen von  mit der
mit der  -Achse an.
-Achse an.
(2 Punkte)
b)
Bestimme rechnerisch die lokalen Extremstellen von  .
.
(7 Punkte)
c)
Die Sekante  verläuft durch den Tiefpunkt
verläuft durch den Tiefpunkt  und den Hochpunkt
und den Hochpunkt  des Graphen von
des Graphen von  .
.
(1)
Zeichne die Sekante  in die Abbildung ein und bestimme rechnerisch die Steigung von
in die Abbildung ein und bestimme rechnerisch die Steigung von  .
.
(2)
Im Bereich von  bis
bis  gibt es Stellen, an denen die Tangente an den Graphen von
gibt es Stellen, an denen die Tangente an den Graphen von  eine größere Steigung besitzt als die Sekante
eine größere Steigung besitzt als die Sekante  .
Gib eine solche Stelle an und begründe deine Angabe mithilfe einer Rechnung.
.
Gib eine solche Stelle an und begründe deine Angabe mithilfe einer Rechnung.
(3 + 3 Punkte)
d)
Der Graph von  wird so in Richtung der
wird so in Richtung der  -Achse verschoben, dass der verschobene Graph genau zwei Nullstellen besitzt.
Gib alle Möglichkeiten einer solchen Verschiebung an.
-Achse verschoben, dass der verschobene Graph genau zwei Nullstellen besitzt.
Gib alle Möglichkeiten einer solchen Verschiebung an.
(3 Punkte)
e)
Die Funktion  ist die Ableitungsfunktion einer Funktion
ist die Ableitungsfunktion einer Funktion  .
Entscheide begründet, z.B. mithilfe des Graphen von
.
Entscheide begründet, z.B. mithilfe des Graphen von  , für jede der beiden folgenden Aussagen
, für jede der beiden folgenden Aussagen  und
und  ob sie wahr oder falsch ist.
ob sie wahr oder falsch ist.
 Der Graph von
Der Graph von  steigt im gesamten Bereich von
steigt im gesamten Bereich von  bis
bis 
 Der Graph von
Der Graph von  besitzt an der Stelle
besitzt an der Stelle  einen lokalen Hochpunkt.
einen lokalen Hochpunkt.
(3 + 3 Punkte)
Aufgabe 4
Der US-Amerikaner Carl Lewis gehört zu den erfolgreichsten Leichtathleten der Sportgeschichte. Einen seiner acht Weltmeistertitel hat er bei den Leichtathletik-Weltmeisterschaften 1991 im  -Lauf gewonnen.
-Lauf gewonnen.
 In dieser Aufgabe wird eine
In dieser Aufgabe wird eine  lange Teilstrecke seines Finallaufes betrachtet. Für diese Teilstrecke wird die Momentangeschwindigkeit in Abhängigkeit von der zurückgelegten Strecke durch die Funktion
lange Teilstrecke seines Finallaufes betrachtet. Für diese Teilstrecke wird die Momentangeschwindigkeit in Abhängigkeit von der zurückgelegten Strecke durch die Funktion  mit
modelliert.
Dabei ist
mit
modelliert.
Dabei ist  die zurückgelegte Strecke in der Einheit
die zurückgelegte Strecke in der Einheit  (d. h.
(d. h.  entspricht
entspricht  ,
,  entspricht
entspricht  usw.).
usw.).  ist die zugehörige Momentangeschwindigkeit in
ist die zugehörige Momentangeschwindigkeit in  Für
Für  beschreibt diese Funktion näherungsweise die Momentangeschwindigkeit von Carl Lewis von der
beschreibt diese Funktion näherungsweise die Momentangeschwindigkeit von Carl Lewis von der  -Markierung bis zur
-Markierung bis zur  -Markierung.
Der Graph von
-Markierung.
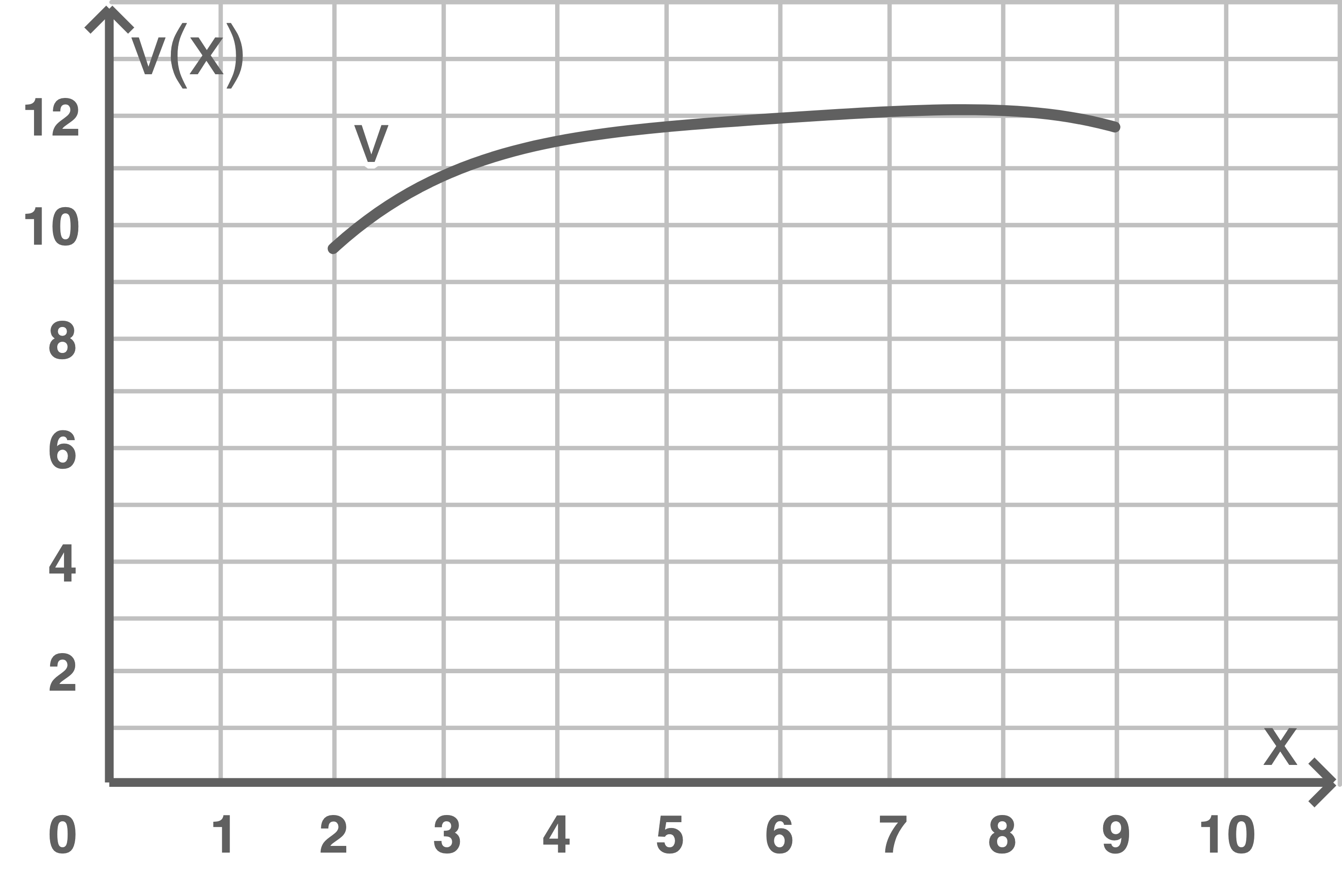
Der Graph von  ist in der Abbildung 2 dargestellt.
ist in der Abbildung 2 dargestellt.
 Die folgenden Teilaufgaben beziehen sich auf die durch die Funktion
Die folgenden Teilaufgaben beziehen sich auf die durch die Funktion  modellierte Momentangeschwindigkeit.
modellierte Momentangeschwindigkeit.

Abbildung 1

Abbildung 2
a)
Bestimme die Momentangeschwindigkeit von Carl Lewis an der  -Markierung auf zwei Nachkommastellen genau.
[Zur Kontrolle: Der auf eine Nachkommastelle gerundete Wert beträgt
-Markierung auf zwei Nachkommastellen genau.
[Zur Kontrolle: Der auf eine Nachkommastelle gerundete Wert beträgt  ].
].
(2 Punkte)
b)
Carl Lewis hat seine maximale Geschwindigkeit in dem Finallauf zwischen der  -Markierung und der
-Markierung und der  -Markierung erreicht.
Bestimme rechnerisch diese maximale Geschwindigkeit.
-Markierung erreicht.
Bestimme rechnerisch diese maximale Geschwindigkeit.
(9 Punkte)
c)
(1)
Carl Lewis hat in seinem Finallauf für die  -Strecke vom Start bis zum Ziel
-Strecke vom Start bis zum Ziel  benötigt.
Weise nach, dass seine Durchschnittsgeschwindigkeit bei diesem Lauf ca.
benötigt.
Weise nach, dass seine Durchschnittsgeschwindigkeit bei diesem Lauf ca.  betragen hat.
betragen hat.
(2)
Ermittle mithilfe der Funktion  nach welcher zurückgelegten Strecke die Momentangeschwindigkeit von Carl Lewis genauso groß wie seine Durchschnittsgeschwindigkeit gewesen ist.
nach welcher zurückgelegten Strecke die Momentangeschwindigkeit von Carl Lewis genauso groß wie seine Durchschnittsgeschwindigkeit gewesen ist.
(2 + 3 Punkte)
d)
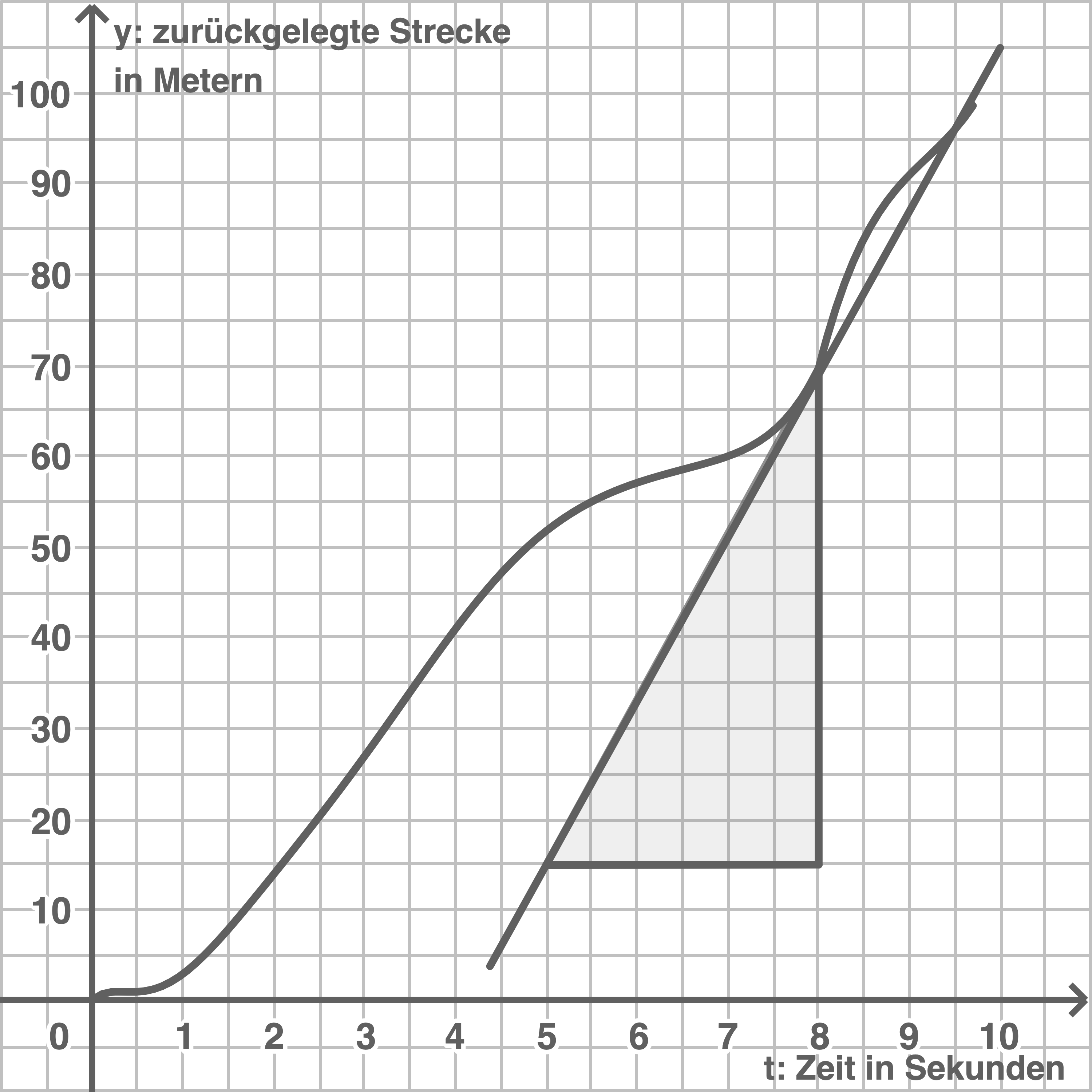
In der Abbildung 3 siehst du das Zeit-Weg-Diagramm einer Bewegung.
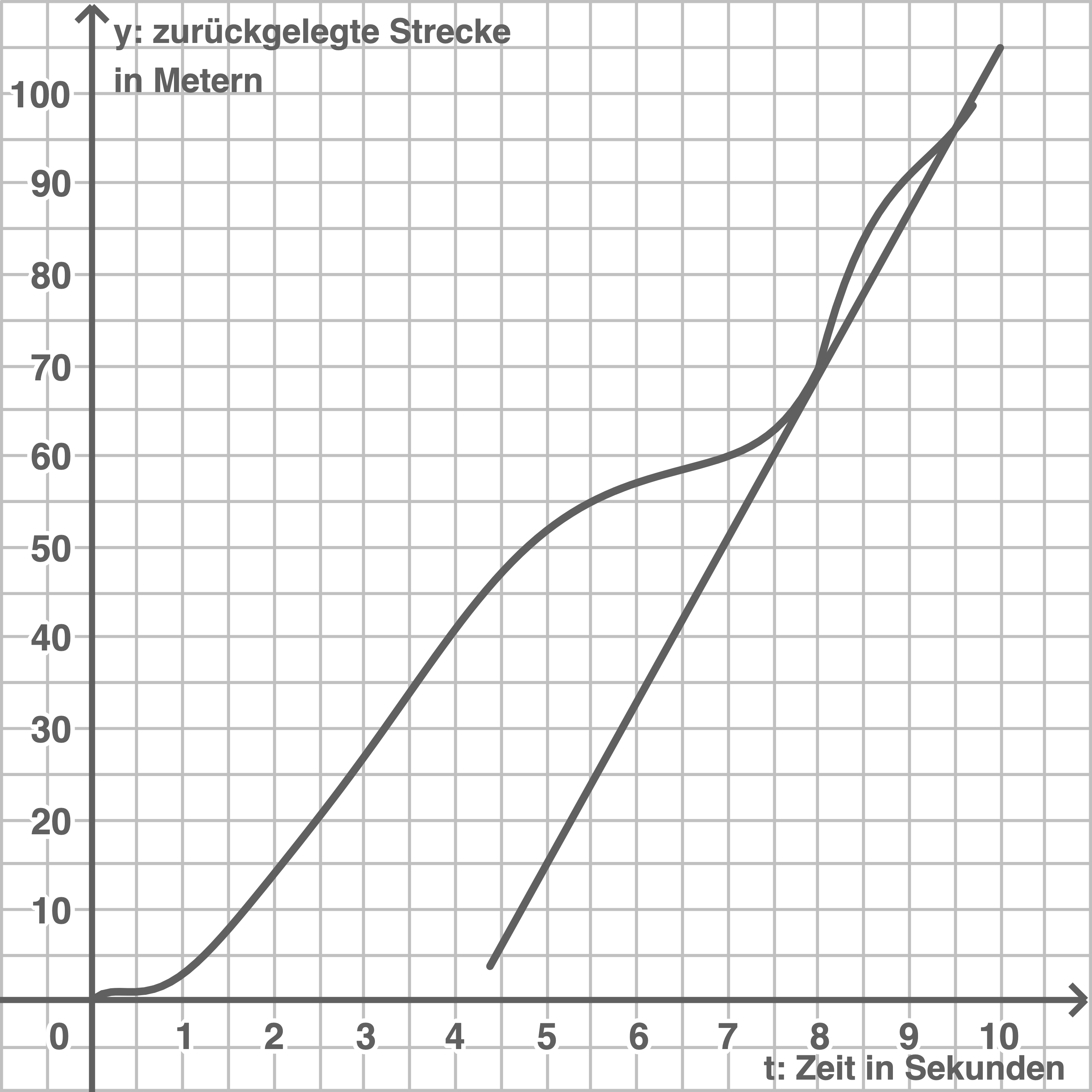 Die
Die  -Werte geben die Zeit in Sekunden und die
-Werte geben die Zeit in Sekunden und die  -Werte die in dieser Zeit zurückgelegte Strecke in
-Werte die in dieser Zeit zurückgelegte Strecke in  an.
Zusätzlich ist die Tangente an den Graphen an der Stelle
an.
Zusätzlich ist die Tangente an den Graphen an der Stelle  dargestellt.
dargestellt.

Abbildung 3
(1)
Bestimme näherungsweise die Steigung dieser Tangente.
(2)
Entscheide begründet, ob es sich bei dem Diagramm aus Abbildung 3 um das Zeit-Weg-Diagramm des Finallaufes von Carl Lewis handeln kann.
(2 + 2 Punkte)
e)
Die Funktion  soll zu einer Funktion
soll zu einer Funktion  transformiert werden, so dass eine Strecke von
transformiert werden, so dass eine Strecke von  Metern nicht mehr durch
Metern nicht mehr durch  sondern durch
sondern durch  eine Strecke von
eine Strecke von  Metern nicht durch
Metern nicht durch  sondern durch
sondern durch  usw. festgelegt wird.
usw. festgelegt wird.
 ist wieder die zugehörige Momentangeschwindigkeit von Carl Lewis in
ist wieder die zugehörige Momentangeschwindigkeit von Carl Lewis in 
(1)
Gib an, durch welche Transformation der Graph der Funktion  in den Graphen der Funktion
in den Graphen der Funktion  überführt wird.
überführt wird.
(2)
Die Funktion  wird durch eine der folgenden Gleichungen beschrieben.
Gib an, welche der Gleichungen die Funktion
wird durch eine der folgenden Gleichungen beschrieben.
Gib an, welche der Gleichungen die Funktion  beschreibt.
beschreibt.








(2 + 2 Punkte)
Lösung 3
a)
b)
1. Notwendiges Kriterium für lokale Extremstellen
![\(\begin{array}[t]{rll}
f](https://www.schullv.de/resources/formulas/e5bef3e2285a5bb9aef37ae2661aec454568563df098ed8bb3dccd213fc54db6_light.svg) 2. Vorzeichenwechselkriterium überprüfen
2. Vorzeichenwechselkriterium überprüfen


 Es liegt also sowohl an der Stelle
Es liegt also sowohl an der Stelle  als auch an der Stelle
als auch an der Stelle  ein Vorzeichenwechsel der Funktionswerte von
ein Vorzeichenwechsel der Funktionswerte von  vor. Beide Stellen sind daher Extremstellen der Funktion
vor. Beide Stellen sind daher Extremstellen der Funktion 
c)
(1)
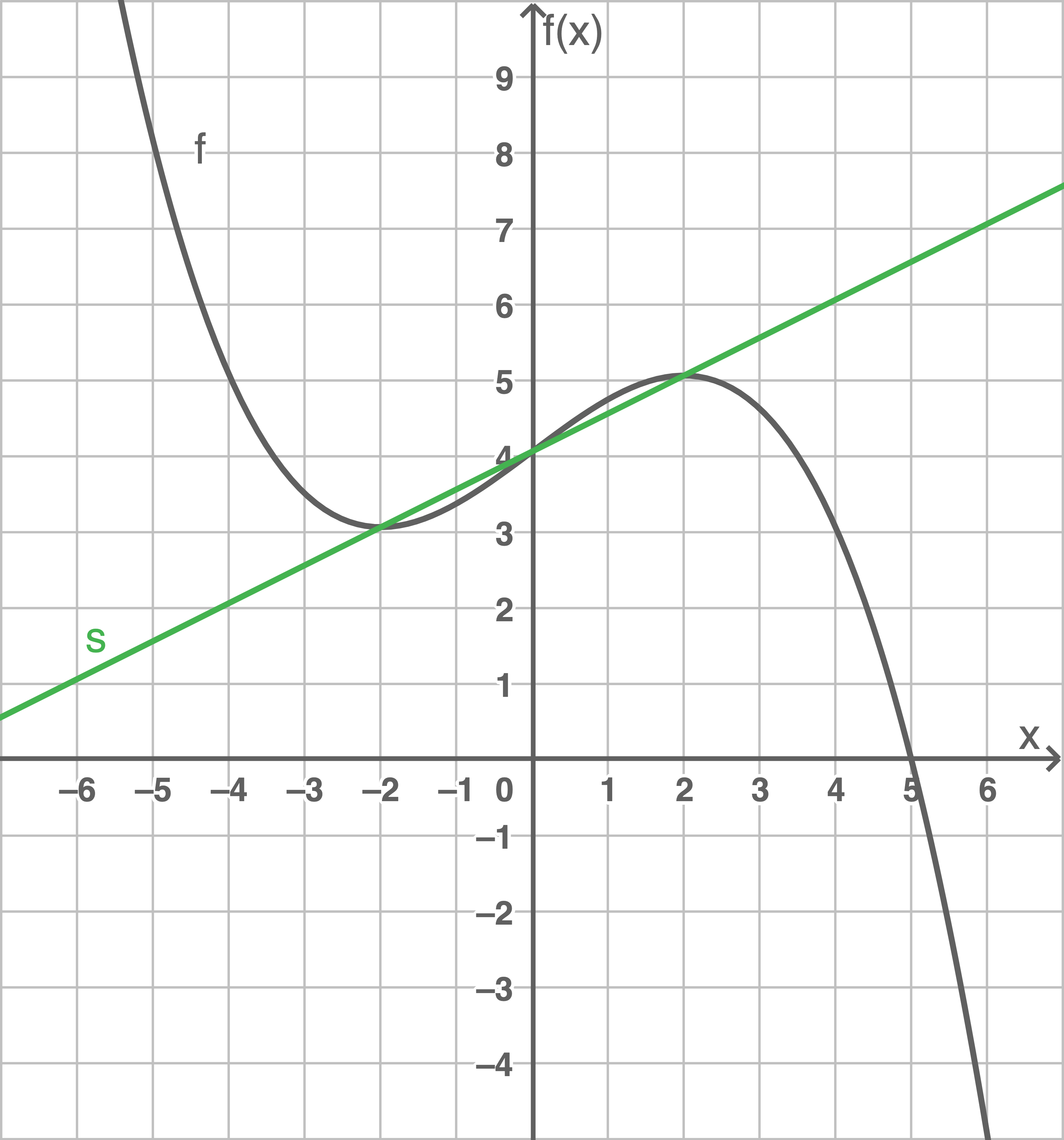
(2)
d)
Möglichkeit 1: Verschiebung des Graphen von  um
um  Einheiten nach unten.
Möglichkeit 2: Verschiebung des Graphen von
Einheiten nach unten.
Möglichkeit 2: Verschiebung des Graphen von  um
um  Einheiten nach unten.
Einheiten nach unten.
e)
Die Aussage (A) ist wahr, denn im genannten Bereich sind alle Funktionswerte von  positiv.
Die Aussage (B) ist ebenfalls wahr, da an der Stelle
positiv.
Die Aussage (B) ist ebenfalls wahr, da an der Stelle  ein Vorzeichenwechsel von positiven zu negativen Funktionswerten von
ein Vorzeichenwechsel von positiven zu negativen Funktionswerten von  vorliegt.
vorliegt.
Lösung 4
a)
b)
1. Notwendiges Kriterium für lokale Extremstellen
2. Vorzeichenwechselkriterium überprüfen

 Daher liegt an der Stelle
Daher liegt an der Stelle  ein Vorzeichenwechsel von positiven zu negativen Funktionswerten von
ein Vorzeichenwechsel von positiven zu negativen Funktionswerten von  und damit ein lokales Maximum von
und damit ein lokales Maximum von  vor. Wegen
vor. Wegen  und
und  liegt bei
liegt bei  auch das absolute Maximum von
auch das absolute Maximum von  im Intervall
im Intervall ![\([2;9]\)](https://www.schullv.de/resources/formulas/0a3e6f921fdedd581e20893482f7388ddf9c3027af51c5a4ffd2618c17f5b944_light.svg) vor.
Nach ca.
vor.
Nach ca.  hat Carl Lewis mit etwa
hat Carl Lewis mit etwa  seine maximale Geschwindigkeit erreicht.
seine maximale Geschwindigkeit erreicht.
c)
(1)
(2)
Die Gleichung  besitzt die Lösungen
besitzt die Lösungen  und
und  mit
mit  und
und 
 liegt nicht im Intervall
liegt nicht im Intervall ![\([2;9].\)](https://www.schullv.de/resources/formulas/6d9ebcc7b2a0607a90ebb4ace597ef3a74398505f7e47230cb6d4245ed10d949_light.svg) Nach
Nach  ist die Momentangeschwindigkeit von Carl Lewis genauso groß wie seine Durchschnittsgeschwindigkeit gewesen.
ist die Momentangeschwindigkeit von Carl Lewis genauso groß wie seine Durchschnittsgeschwindigkeit gewesen.
d)
(1)
Mit dem eingezeichneten Steigungsdreieck ergibt sich für die Steigung der Tangente an der Stelle  ein Wert von ungefähr
ein Wert von ungefähr 

(2)
In der Abbildung 2 kann abgelesen werden, dass die maximale Momentangeschwindigkeit von Carl Lewis knapp über  betragen hat. Somit passt ein Wert von ca.
betragen hat. Somit passt ein Wert von ca.  nicht zum Lauf von Carl Lewis.
nicht zum Lauf von Carl Lewis.
Bei dem Diagramm aus Abbildung 3 kann es sich also nicht um das Zeit-Weg-Diagramm des Laufes von Carl Lewis handeln.
Bei dem Diagramm aus Abbildung 3 kann es sich also nicht um das Zeit-Weg-Diagramm des Laufes von Carl Lewis handeln.
e)
(1)
Der Graph von  geht durch eine Streckung mit dem Faktor
geht durch eine Streckung mit dem Faktor  in
in  -Richtung aus dem Graphen von
-Richtung aus dem Graphen von  hervor.
hervor.
(2)
Richtig ist (C): 