Prüfungsteil A: Ohne Hilfsmittel
Aufgabe 1: Analysis
Die Abbildung zeigt den Graphen der Funktion  mit der Gleichung
mit der Gleichung

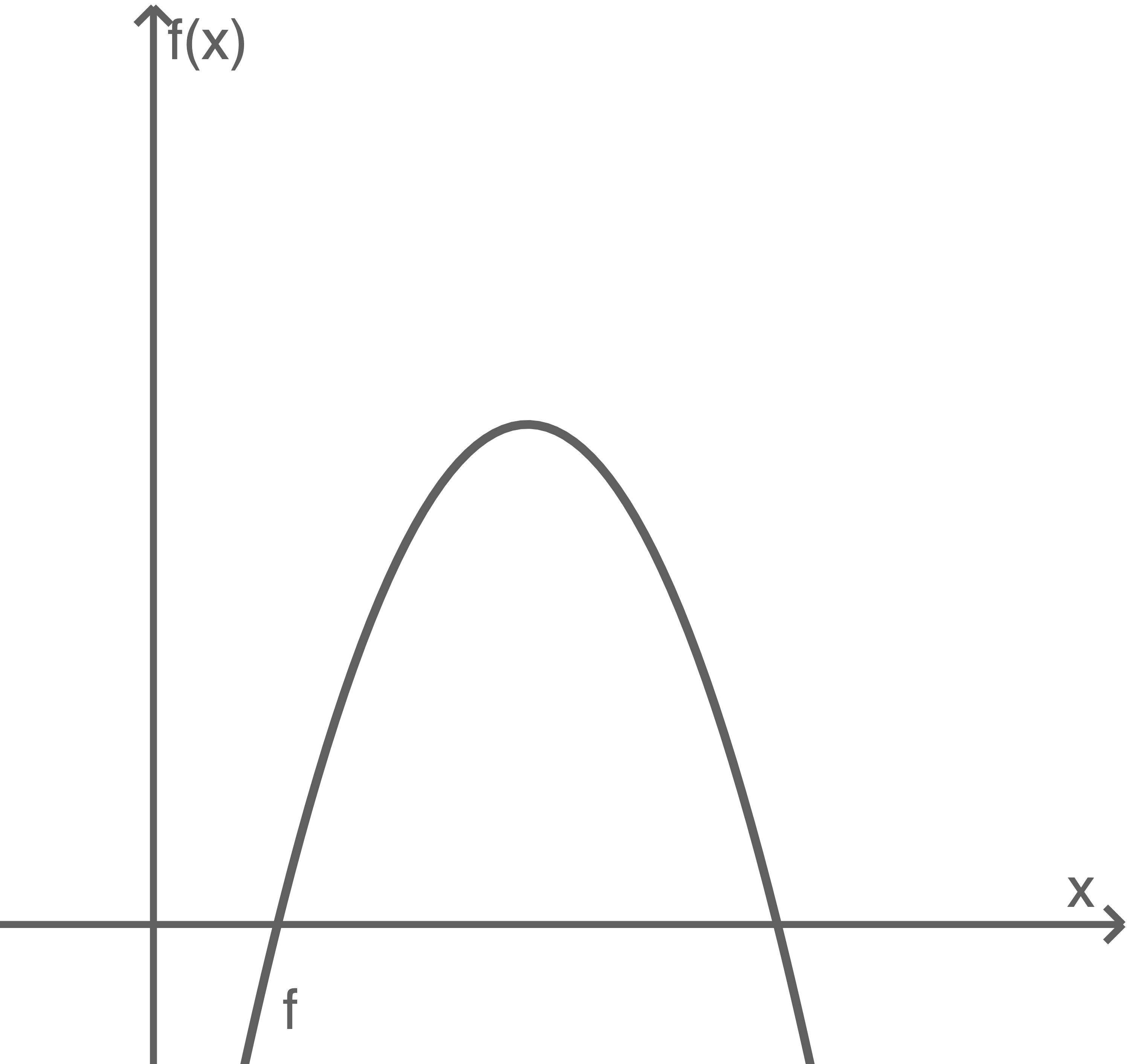

Abbildung
a)
(1) Berechne die Nullstellen der Funktion 
(2) Skizziere in die Abbildung den Graphen der Ableitungsfunktion 
(2 + 2 Punkte)
b)
Ermittle, um wie viele Einheiten der Graph von  nach unten verschoben werden muss, so dass der verschobene Graph nur einen gemeinsamen Punkt mit der
nach unten verschoben werden muss, so dass der verschobene Graph nur einen gemeinsamen Punkt mit der  -Achse besitzt.
-Achse besitzt.
(2 Punkte)
Aufgabe 2: Stochastik
Eine Firma hat einen neuen Wirkstoff gegen Erkältungsbeschwerden entwickelt, dessen Wirksamkeit an erkälteten Versuchspersonen getestet wurde:
der Versuchspersonen erhielten eine Tablette mit dem neuen Wirkstoff, die übrigen Versuchspersonen erhielten eine Tablette ohne Wirkstoff.
- Nach einer Stunde trat insgesamt bei der Hälfte aller Versuchspersonen eine Linderung ein.
der Versuchspersonen erhielten eine Tablette ohne Wirkstoff und verspürten keine Linderung.
a)
Stelle den oben beschriebenen Sachverhalt dar, indem du alle Prozentsätze ermittelst und in die folgende Tabelle einträgst.
| Linderung | Keine Linderung | Gesamt | |
|---|---|---|---|
| Tablette ohne Wirkstoff | |||
| Tablette mit Wirkstoff | |||
| Gesamt |
(3 Punkte)
b)
Eine Versuchsperson verspürt eine Linderung.
Bestimme die Wahrscheinlichkeit, dass sie eine Tablette mit Wirkstoff erhalten hat.
(3 Punkte)
Lösung 1
a)
(1)
(2)
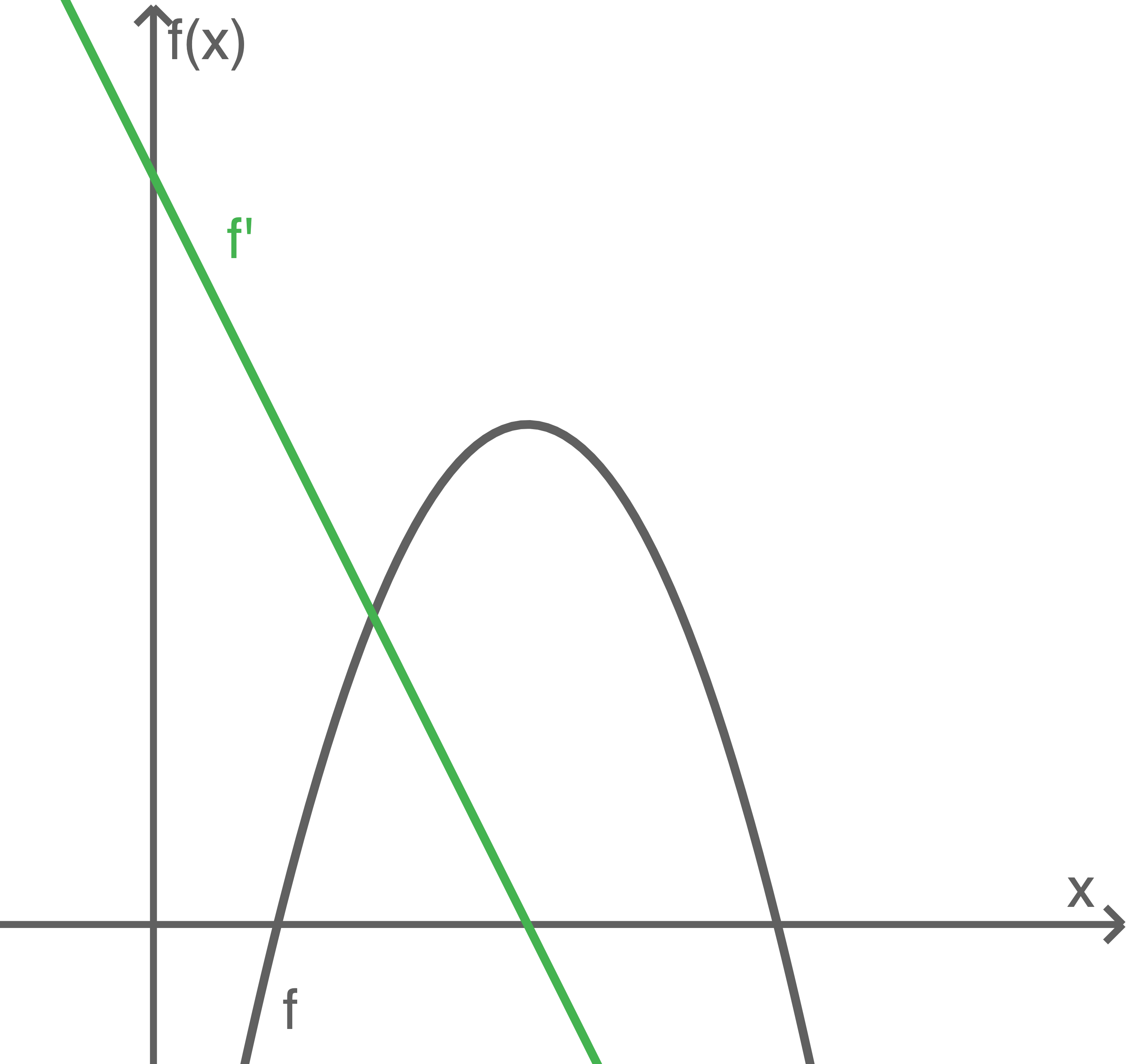
b)
Damit der verschobene Graph mit der  -Achse nur einen gemeinsamen Punkt hat, muss der Scheitelpunkt des Graphen auf der
-Achse nur einen gemeinsamen Punkt hat, muss der Scheitelpunkt des Graphen auf der  -Achse liegen.
Da der Graph symmetrisch ist, liegt die
-Achse liegen.
Da der Graph symmetrisch ist, liegt die  -Koordinate des Scheitelpunkts in der Mitte zwischen den beiden Nullstellen, also an der Stelle
-Koordinate des Scheitelpunkts in der Mitte zwischen den beiden Nullstellen, also an der Stelle  Mit
Mit  folgt, dass der Graph um
folgt, dass der Graph um  Einheiten nach unten verschoben werden muss, um nur einen gemeinsamen Punkt mit der
Einheiten nach unten verschoben werden muss, um nur einen gemeinsamen Punkt mit der  -Achse zu haben.
-Achse zu haben.
Lösung 2
a)
| Tabletten ohne Wirkstoff | Tablette mit Wirkstoff | Gesamt | |
|---|---|---|---|
| Linderung | |||
| Keine Linderung | |||
| Gesamt |
b)
Gesucht ist die Wahrscheinlichkeit dafür, dass es sich um eine Tablette mit Wirkstoff handelt, unter der Bedingung, dass die Versuchsperson eine Linderung verspürt. Mit der Formel für die bedingte Wahrscheinlichkeit folgt:

![\(\begin{array}[t]{rll}
&=& \dfrac{P(\text{Wirkstoff} \cap\text{Linderung})}{P(\text{Linderung})} \\[5pt]
&=& \dfrac{0,48}{0,5} \\[5pt]
&=& \dfrac{0,96}{1} \\[5pt]
&=& 0,96
\end{array}\)](https://www.schullv.de/resources/formulas/a3593aecf97ca3aee69c1c938179879585b35777755c3a28457ed4ea1f7570af_light.svg) Mit einer Wahrscheinlichkeit von
Mit einer Wahrscheinlichkeit von  hat eine Versuchsperson, die eine Linderung verspürt, eine Tablette mit Wirkstoff erhalten.
hat eine Versuchsperson, die eine Linderung verspürt, eine Tablette mit Wirkstoff erhalten.